基于类Gaussian分布的线性扫描极谱重叠峰分离方法-有色金属在线

简介概要

基于类Gaussian分布的线性扫描极谱重叠峰分离方法

来源期刊：中国有色金属学报(英文版)2013年第7期

论文作者：朱红求王国伟阳春华曹宇桂卫华

文章页码：2181 - 2186

关键词：湿法炼锌；类Gaussian分布；重叠峰分离；多分辨率小波分解；NWLS拟合

Key words：zinc hydrometallurgy; Gaussian-like distribution; overlapped peaks resolution; multi-resolution wavelet decomposition; nonlinear weighted least squares fitting

摘要：湿法炼锌浸出液中存在多金属组分，如Zn(II)和Co(II)，针对重叠峰分离提出一种基于类Gaussian分布的线性扫描极谱重叠峰分离方法。通过分析线性扫描极谱曲线的特性构造类Gaussian分布作为待分离重叠峰子峰的模型，并利用多分辨率小波分解确定各子峰波峰和波谷位置，基于该模型及确定值对重叠峰及其导数峰进行非线性加权最小二乘(nonlinear weighted least squares, NWLS)拟合，根据重构参数将重叠峰分离为独立的子峰，实现该类重叠峰的分离。该类重叠峰分离的结果表明：多分辨率小波分解的分辨误差小于1%，NWLS拟合的分离精度高于96%，本方法可以有效分离Zn(II)和Co(II)产生的极谱重叠峰。

Abstract: A resolution method based on Gaussian-like distribution for overlapped linear sweep polarographic peaks was proposed to simultaneously detect the polymetallic components, such as Zn(II) and Co(II), coexisting in the leaching solution of zinc hydrometallurgy. A Gaussian-like distribution was constructed as the sub-model of overlapped peaks by analyzing the characteristics of linear sweep polarographic curve. Then, the abscissas of each peak and trough were pinpointed through multi-resolution wavelet decomposition, the curve and its derivative curves were fitted by using nonlinear weighted least squares (NWLS). Finally, overlapped peaks were resolved into independent sub-peaks based on fitted reconstruction parameters. The experimental results show that the relative error of half-wave potential pinpointed by multi-resolution wavelet decomposition is less than 1% and the accuracy of I_p fitted by NWLS is higher than 96%. The proposed resolution method is effective for overlapped linear sweep polarographic peaks of Zn(II) and Co(II).

Trans. Nonferrous Met. Soc. China 23(2013) 2181-2186

Overlapped peaks resolution for linear sweep polarography using Gaussian-like distribution

Hong-qiu ZHU^1,2, Guo-wei WANG¹, Chun-hua YANG¹, Yu CAO¹, Wei-hua GUI¹

1. School of Information Science and Engineering, Central South University, Changsha 410083, China;

2. School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China

Received 8 October 2012; accepted 26 April 2013

Key words: zinc hydrometallurgy; Gaussian-like distribution; overlapped peaks resolution; multi-resolution wavelet decomposition; nonlinear weighted least squares fitting

1 Introduction

Hydrometallurgy is a major smelting technology of zinc with superiority in environment protection, resource utilization and mineral exploitation [1,2]. However, simultaneous determination of polymetallic components for the leaching solution of zinc hydrometallurgy fails to realize automation, which endangers the optimal operation of smelting process and lowers the metallurgical technology level.

On the aspect of detection method for heavy metal ions, linear sweep polarography has recently attracted more research attention [3,4] due to its rapidity and high sensitivity in simultaneous determination of polymetallic components. However, its application is narrowed in many cases, thereinto, prevalent overlapped peaks resolution problem of detected signal becomes a bottleneck to restrict the development of automation for online analysis while polymetallic components coexist in leaching solution. There are many resolution methods, such as natural logarithm derivative method (NLDM), immune algorithm, fractional-order differential and wave transform. and MONTEJO- BERNARDO [5] proposed an NLDM to accurately estimate peak positions based on a linearization of Gaussian curves, the method was used to detect a certain extent overlapping peaks. SHAO et al [6] summarized the use of basic immune algorithms and its modifications for resolving multi-component, overlapping, gas chromatography-mass spectroscopy signals, the advantages and the disadvantages of IAs were compared with other resolution methods. LI et al [7] presented a new resolution method for the overlapped peak using fractional-order derivative, the specified peak signals were obtained with the fractional-order differentiation filter. JIAO et al [8] described the application of continues wavelet transform for resolving overlapping peaks from capillary electrophoresis. TOFT et al [9] resolved severely overlapping mid-infrared mixture spectra into the pure compounds spectra and concentration profiles using SIMPLe-to-use Interactive Self-modelling Mixture Analysis (SIMPLISMA) and a 2nd order derivative approach. These methods for overlapped peaks focus on the fields of spectra [10], chromatogram [11] and voltammetry peaks [12]. Symmetric normal Gaussian, Lorenzian or Tsallis distribution are usually taken as sub-models for fitting, and then the overlapped peaks are separated into a number of independent peaks, but the methods mentioned above cannot be applied in asymmetry fields. Linear sweep polarographic curve is a strong irregular asymmetry distribution, which leads to the parameters of sub-peaks contained in overlapped curves cannot be effectively resolved.

In this work, a new resolution method based on Gaussian-like distribution for overlapped linear sweep polarographic peaks was proposed. Firstly, a Gaussian-like distribution was constructed as the sub-model of overlapped peaks by analyzing the characteristics of linear sweep polarographic curve. Then, the abscissas of peak and trough were pinpointed as initial values of the model parameters for fitting through multi-resolution wavelet decomposition, the curve and its derivative curves were fitted by using nonlinear weighted least squares. Finally, overlapped peaks were resolved into independent sub-peaks based on fitted reconstruction parameters.

2 Model formulation

Linear sweep polarography is a widely used electrochemical analysis method using half-wave potential, which limits the diffusion current of polarographic curve. However, its curve is a strong irregular asymmetry distribution and there is no simple function representation between polarographic current I and sweep voltage E, which leads to the parameters of sub-peaks contained in overlapped curves cannot be effectively resolved. To solve the problem, a distribution is built to fit the linear sweep polarographic curve, then the sub-peaks are reconstructed based on the fitted parameters, which lays a foundation for qualitative and quantitative analysis of polymetallic components coexisting in the leaching solution of zinc hydrometallurgy.

2.1 Characteristic analysis on linear sweep polarographic curve

The linear sweep polarographic curve is shown in Fig. 1, where E_p, E_p/2, I_p and I_p/2 denote the peak potential, half-wave potential, limiting diffusion current and half-wave current, respectively. The linear sweep polarographic curve has the following characteristics according to analysis: 1) asymmetry; 2) the left side (E>E_p) can be approximated as a Gaussian distribution; 3) the difference between the curve and criterion Gaussian distribution obeys an “S” type distribution described by arc tangent function in this study. Meanwhile, the determination results indicate that residual current can be described as a linear function, which affects the analysis of zero-order and first-order polarographic curves.

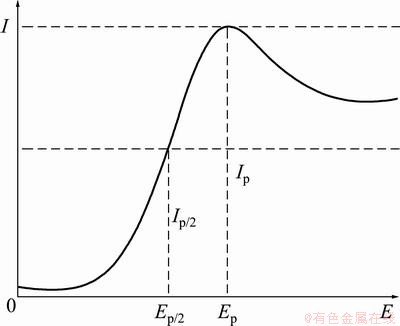
Fig. 1 Linear sweep polarographic curve

2.2 Gaussian-like distribution construction

The linear sweep polarographic curve of monocomponent is approximately expressed by a linear combination of Gaussian distribution, arc tangent function and linear function based on Section 2.1:

(1)

where i_rc=k′x+b′, k₁, …, k₆, k′ and b′ are the reconstruction parameters of the curve. The Gaussian- like distribution is shown in Fig. 2.

Fig. 2 Structure of Gaussian-like distribution

While polymetallic components coexist in solution, linear sweep polarographic curve can be approximately expressed by

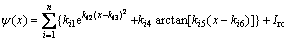(2)

where I_rc=kx+b, k_i₁, …, k_i₆, k and b are the reconstruction parameters of the curve.

To improve the resolution, the first and secondary derivative of Eq. (2) are calculated, and the first derivative δ(x) is obtained as

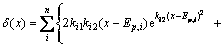
(3)

where E_p,i is the peak position of the i-th curve.

The secondary derivative γ(x) is obtained as

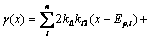
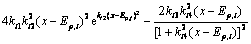(4)

2.3 Constraints for reconstruction parameters

It is effective to pinpoint coordinates of each peak and trough by using multi-resolution wavelet decomposition [13,14], which can separate overlapped peaks accurately by selecting optimal discrete detail D^(j). The optimal decomposition time j is calculated as

(j is integer) (5)

where t is the sampling period of polarographic signal, p_A and p_Bdenote the peak potentials of prepeak and postpeak, respectively. The separating degree R of two-component overlapped peaks is calculated by Eq. (6) as

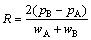(6)

where w_A and w_Bdenote the half-peak widths of prepeak and postpeak, respectively. The half-peak width is defined as the difference between E_p and E_p/2, as shown in Fig. 1.

For the same signal, optimal decomposition time only depends on the separating degree R but not wavelet base.

The following parameters of linear sweep polarographic curve can be calculated by Eqs. (1)-(6): zero-order peak potential E_p,i, first-order prepeak potential E_p,i1, first-order posttrough potential E_p,i2, second-order prepeak potential E_p,i3, second-order trough potential E_p,i4 and second-order postpeak potential E_p,i5. Meanwhile, constraints for Eqs. (2)-(4) are obtained based on the micro-deviations of peaks during derivation, the constraint for Eq. (2) is calculated as

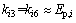(7)

the constraints for Eq. (3) are calculated as

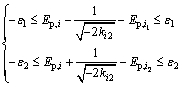(8)

the constraints for Eq. (4) are calculated as

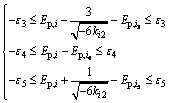(9)

where ε₁, …, ε₅ denote the micro-deviations of peak and trough during derivation. Take ε₁=ε₂=0.05, ε₃=ε₄=ε₅=0.10 as initial values.

3 Experimental

JP-06B microelement analysis instrument electrochemical analysis system was used as detecting platform. A three-electrode with a hanging mercury electrode as working electrode, Ag/AgCl (0.1 mol/L KCl) as reference electrode and dimethylglyoxime a platinum electrode as auxiliary electrode was used.

All the solutions were prepared with analytical grade chemicals and doubly distilled water. HCl, ammonia buffer solution, dimethyglyoxime, Na₂SO₃, sodium citrate, OP-10 and NaNO₂were used as supporting electrolytes.

Confect mixtures containing Zn(II) (34 mg/L) and Co(II) (0.1 mg/L) with a certain amount of standard solution were put into an electrolytic cell. The adding order of solutions was HCl, ammonia buffer solution, DMG, Na₂SO₃, sodium citrate, OP-10, NaNO₂ and measured sample solution. The temperature was maintained at 20 °C and pH=8.26. The mixtures were measured by linear sweep polarography with JP-06B microelement analysis instrument electrochemical analysis system. The scanning potential was in the range of -1.3 to -0.9 V, the scan rate was 25 mV/s, and the standing time was 8 s. The signals detected were put into the test platform to be processed.

As shown in Fig. 3, the linear sweep polarographic curves of Co(II) and Zn(II) are overlapped in the voltage range of -1.3 to -0.9 V.

4 Results and discussion

In order to verify the feasibility and effectiveness of the proposed method for the overlapped linear sweep polarographic peaks, detected signal is transmited to the test platform, then Gaussian-like distribution is taken as sub-peak model. The abscissas of all peaks and troughs are pinpointed by multiresolution wavelet decomposition, namely substitute half-peak widths of the two sub-peaks w _Aand w _B, peak potentials of prepeak and postpeak p_A and p_Binto Eq. (6) to obtain the overlapped peaks separating degree R, then sampling period t and Eq. (5) are combined to gain the optimal decomposition time j. For the detected signal shown in Fig.3, the optimal decomposition time j is 8.

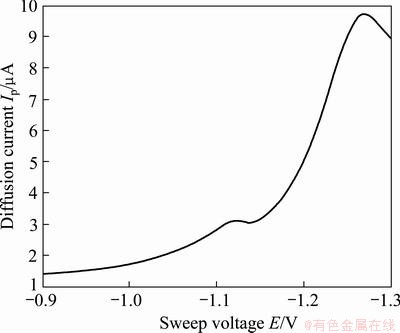
Fig. 3 Zero-order overlapped linear sweep polarographic peaks of Co(II) and Zn(II)

4.1 Resolution results

The abscissas of peak and trough are pinpointed based on multiresolution wavelet decomposition by using the optimal decomposition time. The decomposition result in MATLAB based on zero-order curve is shown in Fig. 4. The optimal discrete detail d₈ indicates that the peak potential of Co(II) 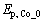= -1.11 V, and the potentials of the first and second order curves can be calculated simultaneously. All the data are listed in Table 1.

To eliminate the influence of stray peaks and residual current, NWLS [15,16] is applied for fitting. The resolution speed and accuracy are comprehensively considered, and the weight function is designed as Eq. (10) due to the resolution focused on the two overlapped peaks.

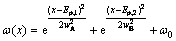(10)

where E_p,1and E_p,2 denote the peak potentials of the two zero-order polarographic curve, respectively, reference weight ω₀is introduced to improve the fitting correlation degree, ω₀∈[0,1].

The fitting results are shown in Figs. 5-7.

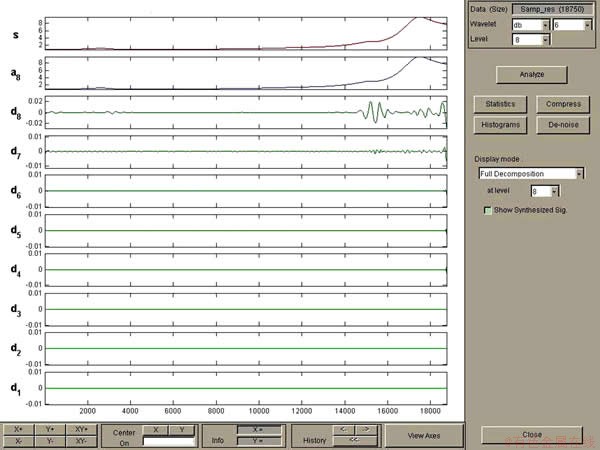
Fig. 4 Zero-order decomposition map of Co(II) and Zn(II)

Table 1 Potentials of peak and trough calculated by multi- resolution decomposition

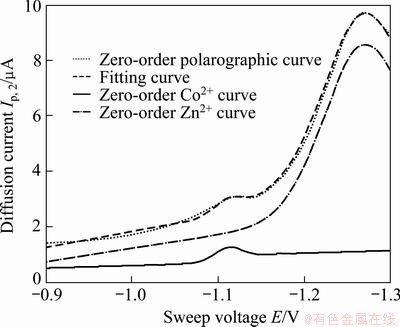
Fig. 5 Zero-order resolution results for Co(II) and Zn(II)

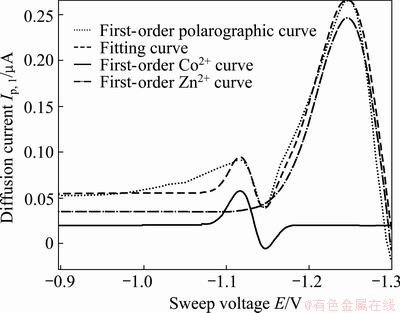
Fig. 6 First-order resolution results for Co(II) and Zn(II)

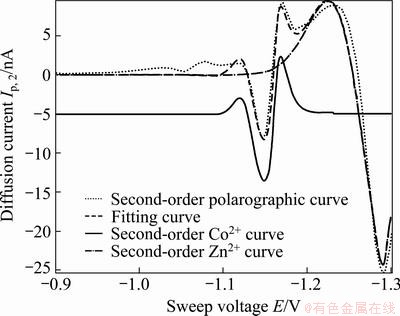
Fig. 7 Second-order resolution results for Co(II) and Zn(II)

4.2 Performance analysis

Due to the asymmetry of Gaussian-like distribution, it is difficult to map the undetermined parameters by using the proposed resolution method, which provides constraints and optimal initial values. Two conclusions can be drawn from the fitting results by selecting different initial values for fitting.

1) The speed of NWLS fitting is largely raised due to setting optimal initial values gained by multi- resolution decomposition and introducing constraints for reconstruction parameters;

2) The stability of NWLS fitting is also greatly improved by introducing constraints for reconstruction parameters.

The fitting correlation degree and mean square deviation are listed in Table 2. The following conclusions for fitting results can be drawn from Figs. 5-7 and Table 2.

Table 2 Statistics of fitting correlation degree and mean square deviation

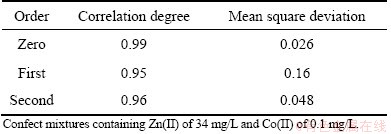
As seen from Table 2, zero-order has the maximum correlation degree (0.99) and the minimum mean square deviation (0.026), those of the second-order are 0.96 and 0.048, and those of the first-order are 0.95 and 0.16. The maximum relative error appears on the interval of [-1 V, -1.13 V] due to stray peaks generated by the reaction occurred between supporting electrolyte and sample leaching solution. The analysis precision of determined components can be improved by selecting different weights.

The validation and reliability are further verified according to the experimental comparisons of monocomponent as listed in Table 3.

Table 3 Fitting results and experimental comparisons

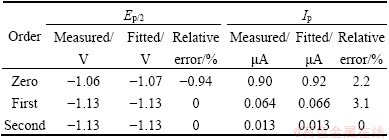
Tables 2 and 3 indicate that the relative error of E_p/2 of zero order is less than 1%, and that of the first order and second order are 0, which proves that multi- resolution wavelet decomposition has the ability to pinpoint potentials of each overlapped sub-peak. The relative error of I_p of zero order is 2.2%, and that of the first order and second order is 3.1% and 0, which proves that NWLS fitting is effective to resolve overlapped linear sweep polarographic peaks of Zn(II) and Co(II).

5 Conclusions

1) A new resolution method was proposed for overlapped linear sweep polarographic peaks. Detection for the polymetallic components coexisted in leaching solution of zinc hydrometallurgy was taken as background.

2) A Gaussian-like distribution was built to describe the sub-peak of the overlapped peaks and multi- resolution wavelet decomposition was used to pinpoint the characteristic parameters of overlapped peaks. Based on the constraints of reconstruction parameters, overlapped curves resolution was implemented by using NWLS fitting. The experimental results show that the proposed method is feasible and effective for overlapped linear sweep polarographic signals of Zn(II) and Co(II).

3) The resolution of overlapped peaks is successfully extended into asymmetric sub-peak field by constructing asymmetric distribution, which provides references for other overlapped peaks composed by asymmetric sub-peaks.

References

[1] J. Statistical analysis of cobalt removal from zinc electrolyte using the arsenic-activated process [J]. Hydrometallurgy, 2004, 73(1-2): 123-132.

[2] TIAN Guo-cai, LI Jian, HUA Yi-xin. Application of ionic liquids in hydrometallurgy of nonferrous metals [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(3): 513-520.

[3] XU Mao-tian, SONG Jun-feng, LIANG Yao-dong. Rapid determination of telmisartan in pharmaceutical preparations and serum by linear sweep polarography [J]. Journal of Pharmaceutical and Biomedical Analysis, 2004, 34(3): 681-687.

[4] ZHANG Li-juan, ZHANG Shao-feng, WAN You-zhi. Voltammetric behavior of methaqualone and its determination by single-sweep oscillopolarography [J]. Talanta, 2003, 59(5): 1009-1013.

[5] A, MONTEJO-BERNARDO J M. Natural logarithm derivative method: A novel and easy methodology for finding maximums in overlapping experimental peaks [J]. Spectrochimica Acta, Part A: Molecular and Biomolecular Spectroscopy, 2009, 74(3): 714-718.

[6] SHAO Xue-guang, LIU Zhi-chao, CAI Wen-sheng. Resolving multi-component overlapping GC-MS signals by immune algorithms [J]. Trends in Analytical Chemistry, 2009, 28(11): 1312-1321.

[7] LI Yuan-lu, TANG Hui-qiang, CHEN Hai-xiu. Fractional-order derivative spectroscopy for resolving simulated overlapped Lorenztian peaks [J]. Chemometrics and Intelligent Laboratory Systems, 2011, 107(1): 83-89.

[8] JIAO Long, GAO Su-ya, ZHANG Fang, LI Hua. Quantification of components in overlapping peaks from capillary electrophoresis by using continues wavelet transform method [J]. Talanta, 2008, 75(4): 1061-1067.

[9] TOFT J, CUESTA SANCHEZ F, van den BOGAERT B, LIBNAU F O, MASSART D L. Resolution of overlapping mid-infrared spectra using SIMPLISMA and a second-order derivative approach [J]. Vibrational Spectroscopy, 1996, 10(2): 125-138.

[10] HUA Yao-gai, LIU Jin-yang, LI Wei. Resolution of overlapping spectra by curve-fitting [J]. Analytica Chimica Acta, 2005, 538(1-2): 383-389.

[11] GOICOECHEA H C, CULZONI M J, GIL GARCIA M D, MARTINEZ G M. Chemometric strategies for enhancing the chromatographic methodologies with second-order data analysis of compounds when peaks are overlapped [J]. Talanta, 2011, 83(4): 1098-1107.

[12] HUANG W, HENDERSON T L E, BOND A M, OLDHAM K B. Curve fitting to resolve overlapping voltammetric peaks: Model and examples [J]. Analytica Chimica Acta, 2005, 304(1): 1-15.

[13] HE L, HUANG G H, ZENG G M, LU H W. Wavelet-based multiresolution analysis for data cleaning and its application to water quality management systems [J]. Expert Systems with Applications, 2008, 35(3): 1301-1310.

[14] ZHANG Zhao, CAO Fa-he, CHENG Ying-liang, ZHANG Jian-qing, WANG Jian-ming, CAO Chu-nan. Analysis of corrosion behavior of LY12 in sodium chloride solution with wavelet transform technique [J]. Transactions of Nonferrous Metals Society of China, 2002, 12(6): 1206-1209.

[15] DRAGAN J, MIRTA B, RUDOLF S. On the existence of the nonlinear weighted least squares estimate for a three-parameter Weibull distribution [J]. Computational Statistics and Data Analysis, 2008, 52(9): 4502-4511.

[16] NI B J, ZENG R J, FANG F, XU J, SHENG G P, YU H Q. A novel approach to evaluate the production kinetics of extracellular polymeric substances (EPS) by activated sludge using weighted nonlinear least-squares analysis [J]. Environmental Science and Technology, 2009, 43(10): 3743-3750.