J. Cent. South Univ. (2021) 28: 1570-1583

DOI: https://doi.org/10.1007/s11771-021-4716-8

Predictions of friction and flash temperature in marine gears based on a 3D line contact mixed lubrication model considering measured surface roughness

SHI Xiu-jiang(史修江)¹, LU Xi-qun(卢熙群)¹, HE Tao(何涛)², SUN Wen(孙文)¹,

TONG Qing-shun(佟庆顺)³, MA Xuan(马旋)¹, ZHAO Bin(赵滨)¹, ZHU Dong(朱东)¹

1. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China;

2. Department of Mechanical Engineering, Northwestern University, Evanston, IL 60208, USA;

3. JIER Machine-Tool Group Co., Ltd, Jinan 250022, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021

Abstract: Wear and scuffing failures often occur in marine transmission gears due to high friction and flash temperature at the interface between the meshing-teeth. In this paper, a numerical solution procedure was developed for the predictions of transient friction and flash temperature in the marine timing gears during one meshing circle based on the 3D line contact mixed lubrication simulation, which had been verified by comparing the flash temperature with those from Blok’s theory. The effect of machined surface roughness on the mixed lubrication characteristics is studied. The obtained results for several typical gear pairs indicate that gear pair 4-6 exhibits the largest friction and the highest interfacial temperature increase due to severe rough surface asperity contacts, while the polished gear surfaces yield the smallest friction and the lowest interfacial temperature. In addition, the influences of the operating conditions and the gear design parameters on the friction-temperature behaviors are discussed. It is observed that the conditions of heavy load and low rotational velocity usually lead to significantly increased friction and temperature. In the meantime, by optimizing the gear design parameters, such as the modulus and the pressure angle, the performance of interfacial friction and temperature can be significantly improved.

Key words: gears; 3D line contact; mixed lubrication; surface roughness; friction; flash temperature

Cite this article as: SHI Xiu-jiang, LU Xi-qun, HE Tao, SUN Wen, TONG Qing-shun, MA Xuan, ZHAO Bin, ZHU Dong. Predictions of friction and flash temperature in marine gears based on a 3D line contact mixed lubrication model considering measured surface roughness [J]. Journal of Central South University, 2021, 28(5): 1570-1583. DOI: https://doi.org/10.1007/s11771-021-4716-8.

1 Introduction

Timing transmission gear is a kind of involute spur gear, which is often associated with crankshaft and camshaft to control the working process of marine engines. The performance of timing transmission gears may have direct influences on the efficiency and reliability of marine engines. However, in recent years, with the continuous performance improvements related to the parameter optimization for the operating power, torque and speed of marine engines, the timing transmission gears are facing more severe working environments. High contact pressure, high sliding velocity and transient fluctuated running conditions may make the timing transmission gears operate in harsh mixed lubrication state, where critical surface asperity contacts take place, and even further result in surface failures of wear and scuffing due to the high interfacial friction and flash temperature increase. Now the failures of timing transmission gears (such as wear, and scuffing) have become the important factors affecting the performance and service life of the internal combustion engine.

Most previous analyses for friction and temperature in spur gears were based on the 2D line contact EHL models with either smooth surfaces or stochastic roughness. For example, the early numerical study by ZHU et al [1] reported a computational procedure through a smooth surface EHL analysis to predict the friction force and flash temperature. Later, considering the effect of 3D surface roughness, the line contact mixed lubrication models for simulating friction-temperature performance were developed. Based on the stochastic mixed lubrication simulation with both Newtonian and Ree-Eyring fluids, KUMAR et al [3] analyzed the integrated effects of temperature, roughness and dynamic load on the friction in a TEHL line contact. Later, the distributions of frictional shear stress and temperature were further investigated by KUMAR et al [4], taking into account the effects of viscous heating and shear thinning. ZHANG et al [5] presented a numerical method to study the frictional mechanisms in a line contact mixed lubrication, and the friction behaviors influenced by the boundary film, the hydrodynamic lubricant film and the solid-to-solid contact. SIMON [6, 7] predicted the oil film pressure, thickness, temperature, and on power losses of spiral bevel gears and hypoid gears in EHL and mixed lubrication field.

The experimental investigations for friction in line contacts have also attracted lots of attentions, which focus mainly on the measurements of friction coefficient and temperature by using different apparatuses, such as roller-disc rig [8], roller-roller [9, 10] and disc-disc rig [11]. The development of the numerical line contact EHL analysis plays an important role in friction and temperature predictions for the spur gears. A prediction model for friction coefficient in mixed lubrication contacts was reported by WU et al [12], which had been further employed in the power loss calculation for spur gears. HE et al [13] predicted the dynamic friction forces in spur gears with different friction formulations, including the Coulomb model and the fitting equations based on the lubrication simulations. AKBARZADEH et al [14] developed the TEHL model under the consideration of surface roughness. Considering the coupling effects of gear motion, coating characteristics, lubrication and surface roughness, LIU et al [15] established a numerical elastohydrodynamic lubrication contact model for coated gear pairs. Considering the roughness effect, LI et al [16] proposed a mixed lubrication model for dynamic performance analysis of spur gears, and the force and moments of friction were studied.

The previous numerical lubrication studies [14-16] indicate that the surface roughness often has crucial influence on the interfacial friction and temperature. However, in many previous investigations the micro-asperities were treated stochastically or assumed to be 2D in shape. Naturally, the rough surface usually exhibits a 3D topography, which may have a great influence on the local friction and temperature distributions. In 2009, the mixed lubrication model of line contact with 3D real surface roughness was firstly built by REN et al [17], and the 3D distributions of film thickness and film pressure were predicted. Later, ZHU et al [18] calculated the subsurface stress and predicted the fatigue life due to micro-pitting using the 3D mixed lubrication model of line contact by REN et al [17]. Later, HE et al [19] further developed the line contact plasto-EHL (PEHL) model with 3D machined roughness.

Until now, few friction-temperature studies in line contact lubrication of spur gears with 3D roughness have been reported. The existing 3D mixed lubrication model for line contact problems [17] has made the EHL analysis capable of handling 2D infinitely long line contact with 3D deterministic roughness topograpgy. In this paper, based on our 3D mixed lubrication model of the spur gear built in 2019 [20], the friction-temperature predictions are further developed for the timing transmission spur gears in marine engine under the considerations of real 3D machined surface roughness and transient tooth meshing. The presented model can be used to provide technical support for predicting the surface failures of wear and scuffing of the gear teeth, and also can guide optimizations of the gear design.

2 Transient-meshing model for spur gears

2.1 Transient-load sharing

In one meshing cycle of a pair of gear teeth, an alternating form of double-pairs of teeth loading and single-pair of teeth loading is shown in Figure 1, and the following is the corresponding simplified load sharing equation:

                 (1)

where w₀ is a constant line contact load, t is the meshing time, and w represents the transient load during one meshing cycle.

2.2 Transient-curvature

In Figure 1, the geometry of line contact between two gear teeth is equivalent to that of a cylinder against a plane, and the equivalent radius R is calculated by:

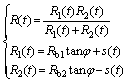                       (2)

where R₁ and R₂ are the radii of two contacting cylinders, respectively; R_b1 and R_b2 represent the base circle radii of the two gears, respectively; φ is the gear pressure angle; s means the meshing distance from engage-in point to pitch point, which is expressed as:

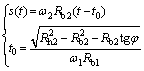                    (3)

where ω₁ and ω₂ mean the angular velocities of the two gears, respectively; t₀ represents the time from engage-in point A to pitch point P; R_h2 is the addendum radii of the gear; R_l2 is the radius of the root circle.

2.3 Transient-velocity

The equivalent entrainment velocity of two meshing gear teeth, U, and the slide-roll ratio, S, are calculated by:

                       (4)

where U₁ and are the surface velocities of two contact cylinders, respectively.

3 Friction-temperature analysis based on 3D mixed lubrication model

The unified mixed lubrication model [17] considering the transient velocity change in spur gears is employed and the Reynolds equation is written as:

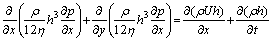  (5)

where ρ and η are the lubricant density and viscosity, which are calculated by the the Dowson-Higginson density equation [21] and the Roelands viscosity equation [22]; p means the interfacial pressure, h means the fluid film thickness, which takes into account the effects of changing curvature of the gear tooth flanks and the real machined surface roughness, expressed as:

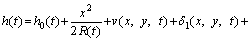
                           (6)

where h₀(t) is the normal approach between the contacting bodies; δ₁ and δ₂ mean the real machined 3D roughness heights of the two surfaces, respectively.

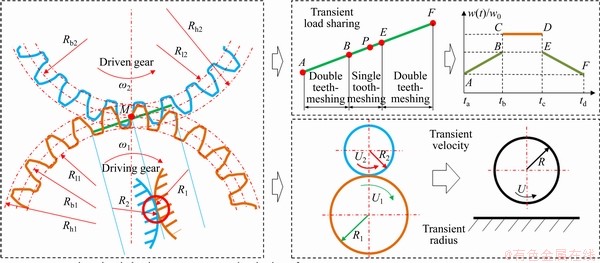
Figure 1 Transient-load sharing, curvature and velocity of spur gears

The load balance equation is also needed when solving the 3D mixed lubrication problem, which can be written as the load balanced by the integration of interfacial pressure within the whole solution domain. In addition, the following boundary conditions are used:

                          (7)

The rheological model proposed by BAIR and WINER [23] is employed to predict the friction coefficient in the lubrication region, which is written as Eq. (8) [1, 2]. In addition, the modified Dyson model by HE et al [24] is used to predict the limit shear stress, and the results had proved that the obtained numerical friction coefficients have well agreements with the testing data.

  (8)

where G_∞ is the ultimate shear modulus; τ_L is the limiting shear stress; both are the properties of lubricant and also the functions of pressure and temperature; σ_q is the composite RMS roughness.

Through the integration of shear stress, the friction force can be obtained. The friction is affected by the temperature. The flash temperature can be calculated based on the theory of a point heat source moving on a half-space. Accordingly, one can have the Volterra integral equations of the second type expressed as follows ([1, 2]), by discreting the intergral equations, and the flash temperatures of two contact surface are obtained.

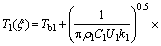
       (9)

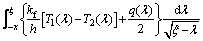      (10)

where T_b1 and T_b2 are the initial surface temperature of the two contacting teeth; ρ₁, ρ₂, C₁, C₂, k₁ and k₂ are the densities, specific heats and heat conductivities of teeth 1 and 2, respectively; q is the heat generated by the interfacial friction.

4 Numerical procedure

The friction and temperature rise on the marine gear tooth surfaces depend mainly on the meshing conditions in the asperity-contact regions. The contact pressure between two meshing teeth is often greater than 1 GPa, and the shear rate is usually larger than 10⁶-10⁷ s^-1, so the shear stress no longer alters linearly with the changing shear strain rate. Therefore, the non-Newtonian fluid model is necessary. In this work, the BAIR-WINER fluid model is employed to solve for the shear stress. The ultimate shear modulus and limiting shear stress are the functions of pressure and temperature, so the friction will be affected by the temperature clearly. Furthermore, friction will also bring friction heat, which will affect the temperature, so the relationship between friction and temperature is a two-way reflection. The calculation of interface temperature is based on the moving heat source theory, which can be expressed as Volterra integral equations of the second type, as shown in Eqs. (9) and (10). By solving the unified Reynolds Eq. (5) in mixed lubrication model considering the transient velocity change in spur gears, the 3D film pressure can be calculated. After that, the rheological model of BAIR-WINER [23] is employed to predict the shear stress in the lubrication region, through the integration of shear stress, the friction force can be obtained; at last, the friction coefficient will be calculated by dividing by the load. The detail flow chart of friction-temperature prediction of the gear teeth based on the 3D mixed lubrication analysis is given in Figure 2.

5 Results and discussions

5.1 Verification of timing gear flash-temperature model on smooth surface

In this section, we take the transmission timing gears of marine engines as the numerical examples. Table 1 gives the design parameters of the gears. The material density of both gears is 7800 kg/m³, the elastic modulus is 206 GPa, and the Poission ratio is 0.3. The density of lubricant is 870 kg/m³, and the lubricant viscosity is 0.075 Pa·s.

In order to examine the friction-temperature model for the spur gear pair built in this paper, Figure 3 compares the obtained flash temperature of the timing gear pair 3-4 with those from the following fitting equation of BLOK [25],

          (11)

where f is the friction coefficient; w is load per unit of length; λ₁ and λ₂, ρ₁ and ρ₂, c₁ and c₂ are thermal conductivities, specific heats, and the densities of the two solids, respectively; u₁ and u₂ are the velocities of the two solids, respectively; b₀ means the Hertzian half width.

As shown in Figure 3, the flash temperatures under different working conditions are presented. The results show that the distributions of the flash temperature along the line of action from two methods agree well, and the maximum values appear at the engage-in and engage-out points, and the minimum values all occur at the pitch point.

Figure 2 Friction and temperature predictions for gear pairs on basis of 3D mixed lubrication simulations in line contacts

Table 1 Geometric parameters of timing gears

Figure 3 Flash temperature verification at 500 kW under different speeds

However, the presented values are smaller than the Blok’s ones, because the presented method is based on lubrication theory and Blok’s theory is limited to the dry-contact results and simplified in some ways, which means the presented results are more closer to the actual solution. In addition, in BLOK’s equation, the effects of surface roughness are neglected, which have significant influence on flash temperature. Our model has no limitations on this problem.

5.2 Friction-temperature analyses for different transmission gear pairs

The dynamic-meshing parameters along the line of action with different gear pairs are presented in Figure 4. The transmitted power is 500 kW, and the speed of driving gear is 600 r/min. The dynamic-meshing parameters include the dry contact stress, the equivalent radius, the rolling velocity and the slide-roll ratio, which clearly show different variations and distributions for different meshing gear pairs. Due to the larger radius of curvature, the entrainment velocities of gear pair 1-2 appear to be on a higher level. The slide-roll ratios of gear pair 3-4 are higher than those of other gear pairs because of the large velocity difference of the two gears. However, the higher Hertizian contact stress occurs in gear pairs 4 and 6, which is largely caused by the smaller contact width of gear 6.

Figure 5(a) shows the machined ground surface contour for one of the timing gear tooth surfaces, which also gives the root mean square (RMS) roughness, R_q1=657.0 nm. And the other surface of meshed tooth is also ground with R_q2=671.1 nm. The existing 3D random distributed roughness on the surfaces will inevitably affect the mixed lubrication behavior, friction coefficient and temperature rise.

Figure 5(b) presents the variations of friction coefficient μ in one meshing-cycle for different marine gear pairs, within the solution domain of -4.5b≤x≤1.5b and -0.75b≤y≤0.75b (b is Hertzian half width). The grid number in the x direction is 256, and that in the y direction is 64. The pressure convergent criterion is set to be 10^-5. The fluctuations of friction coefficient are clearly observed that they are caused significantly by the roughness effect. The friction first increases, and rises to its maximum value near the pitch point, then goes suddenly down to 0 at pitch point because of the theoretically zero sliding there. A similar variation pattern appears after the pitch point, and the entire distribution is roughly symmetric about the pitch point, as shown in Figure 5(b). In addition, the friction coefficient variations of gear pairs 3-4 and 4-6 demonstrate larger values due to the higher sliding and stress.

The variations of the maximum flash temperature rise for different gear pairs in one meshing-cycle are illustrated in Figures 5(c) and (d), which reveal that the maximum temperature also has the clear rough fluctuations, but the temperature rise decreases firstly, and gets down to the minimum value of nearly 0 at the pitch point, then increased again. Besides, the gear pair 4-6 gives apparently larger temperature than other pairs, and the local maximum temperature rise reaches 180 °C, which is caused mainly by the very large contact stress of gear pair 4-6.

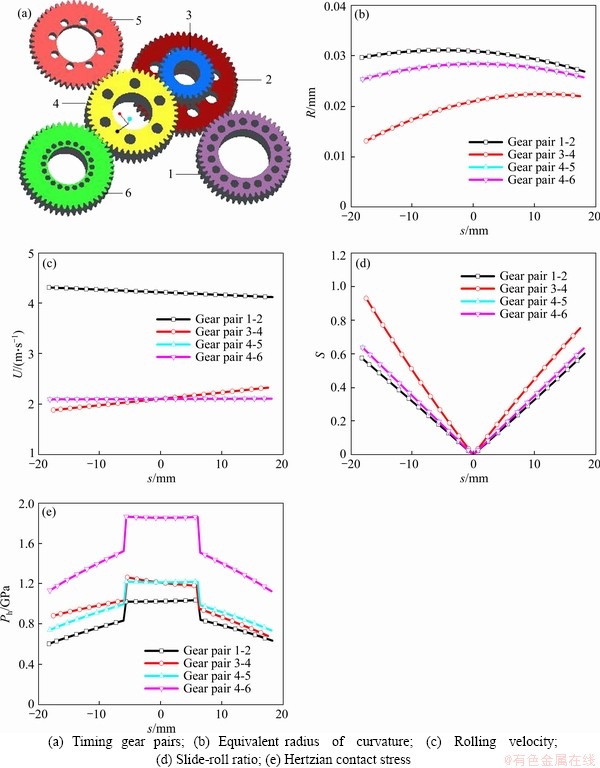
Figure 4 Transient-meshing parameters of marine transmission timing gears in one meshing cycle:

Figure 6 further presents the film thickness and contact area ratio variations of the marine gear pair 4-6, under the same working conditions with the ground roughness. As shown, the minimum film thickness h_min is always zero and even the central film thickness h_cen in the meshing process frequently becomes 0, indicating that the contacts always exist in the meshing process. The central film thickness fluctuates quite randomly because of the effect of 3D ground roughness. The ratio of contact area, W_a, is also shown in Figure 6(a), and its maximum value is closed to 12%. The film thickness contours at the engage-in point, the pitch point and the engage-out point are given in Figures 6(b)-(d), respectively. The results indicate that the film thickness shows clear 3D distributions, which can hardly be approximated by using the simplified 2D mixed lubrication model, and the contact region at the pitch point is larger than that at the engage-in and engage-out locations.

Figure 5 Variations of friction coefficient and maximum temperature rise during one meshing-cycle for different gear pairs:

Figure 6 Contact area ratio and film thickness distributions for timing gear pair 4-6:

5.3 Friction-temperature analysis with different machine process

Figures 7(a)-(c) show roughness height contours of the other three different machined surfaces for one of the gear contact locations, which include polished, honed and shaved rough surfaces. The root mean square (RMS) roughness equal to 149.2, 346.3 and 886.4 nm, respectively.

The effects of different machining processes on the friction coefficient during one meshing-cycle and the temperature rise at transition point of the marine gear pair 4-6 are presented in Figure 7(d), the power is 500 kW, and the velocity of driving gear 3 is 600 r/min. As shown from Figure 7(d), the shaved surface has the largest area of high temperature, and the polished surface has smallest area of high temperature. As for the friction coefficient, the highest value appears on the shaved surface, and then on the honed surface, the lowest value occurs with the polished surface. The main reason is that the localized pressure peaks caused by the shaved roughness are higher, thus generating more heat.

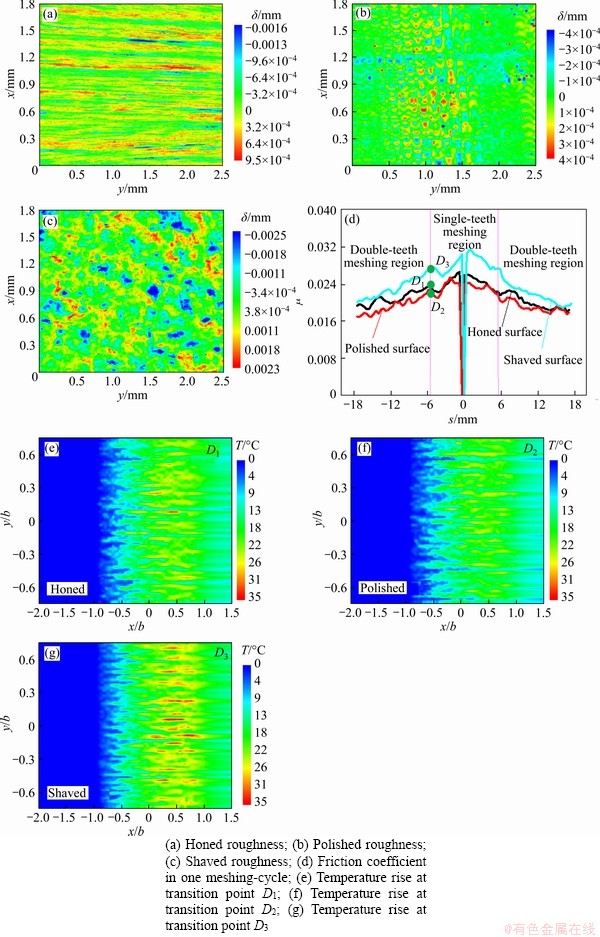
Figure 7 Machining process effect on friction-temperature behaviors in timing gear pair 4-6:

5.4 Effects of operating conditions on interfacial friction and temperature

The velocity effects on the maximum interfacial temperature and friction in one meshing-cycle of the timing gear pair 4-6 with polished surfaces are investigated and the results are plotted in Figure 8. The power is 500 kW. The maximum interface temperature and friction coefficient get decreased with the velocity increase, the maximum friction coefficient is close to 0.06 at velocity of 300 r/min, and then reduces to 0.01 as the velocity is increased to 1200 r/min. This is because the film thickness increases with the increasing velocity. The maximum interfacial temperature is also decreased with the increasing velocity. The main reason is the load becomes smaller as the velocity increases under the condition of constant power. This causes reduced tooth contact pressure.

Figure 8 Velocity effect on interfacial friction and maximum temperature during one meshing cycle:

Figure 9 presents the power effect on the interfacial temperature and friction in one meshing-cycle of the marine gear pair 4-6 with polished surfaces. The velocity of the driving gear 3 is 600 r/min. As shown in this figure, the areas of high temperature and higher friction coefficient increased with the increasing power, but the increasing trends of friction coefficients get decreased, and the maximum friction coefficient is close to 0.025 as the power increases to 500 kW; the friction coefficient reduces to 0.015 as the power goes down to 100 kW.

5.5 Effects of geometric design parameters on friction-temperature performance

This section shows that the gear geometric design parameters may affect the interfacial friction and temperature considerably. It also demonstrates the capability of the model approach for improving the interfacial friction-temperature performance of the timing gear pair by changing the design parameters, which mainly include the pressure angle and the modulus under the conditions of constant rated power and velocity.

5.5.1 Effect of pressure angle

Setting the speed of marine gear 3 as 600 r/min, and setting the input power as 500 kW, the pressure angle effects on friction coefficient and the maximum interface temperature rise in one meshing-cycle, and the temperature profiles along y axis at the engage-out point of gear pair 4-6 with the polished surfaces are presented in Figure 10. As shown, the friction coefficient becomes smaller with the increase of the pressure angle, and the maximum value approaches 0.06 as the pressure angle is getting close to 16°. The friction coefficient reduces to 0.035 when the pressure angle increases to 22°. The maximum interfacial temperature also decreases clearly from a value above 200 °C down to about 100 °C as the pressure angle increases from 16° to 22°. This is because the increasing pressure angle leads to the reduction of the contact stress. It shows that the increase in pressure angle may play an active role in improving the friction and temperature performance of the timing gear pair.

Figure 9 Power effects on friction coefficient in one meshing-cycle and temperature rise at transition point:

5.5.2 Effect of modulus

Figure 11 displays the effect of modulus on friction coefficient and interfacial temperature rise along the line of action, and the temperature profiles along the x axis at the engage-out position of the marine gear pair 4-6 with the polished surfaces. The gear pressure angle is 20°, the velocity is 600 r/min, and the power is 500 kW. It is observed that with the increase of the modulus, the trends of friction and maximum interfacial temperature variations during one meshing-cycle remain the same, but the length of the meshing line is increased. The maximum friction coefficient is above 0.04 when the modulus equals 6. This indicates that a large friction between the contacting surfaces occurs, and the film breakdown will take place. However, the overall friction becomes lower with the increasing modulus. The friction coefficient drops down below 0.02 as the modulus increases to 8. The maximum interfacial temperature approaches 160 °C when the modulus is 5, which may lead to the increased risk of scuffing failure. Also, the interfacial temperature rise shows an apparent reduction as the modulus increases, and the maximum value reduces to 50 °C as the modulus increases to 8. This indicates that the thermal performance is significantly improved.

6 Conclusions

In this study, on the basis of 3D mixed lubrication model for line contact with real machined surface roughness, the transient friction-temperature analysis of the transimission timing gears during one meshing-cycle has been conducted. The effects of the surface roughness, operating conditions and gear geometric design parameters on the interfacial friction and temperature rise are discussed. The following conclusions can be drawn based on the obtained results.

1) The gear pair 4-6 has the largest fiction and interfacial temperature rise because of the smaller contact width and the higher contact stress. The results of film thickness and contact ratio indicate that the asperity-contacts between tooth surfaces always exist during the whole meshing cycle.

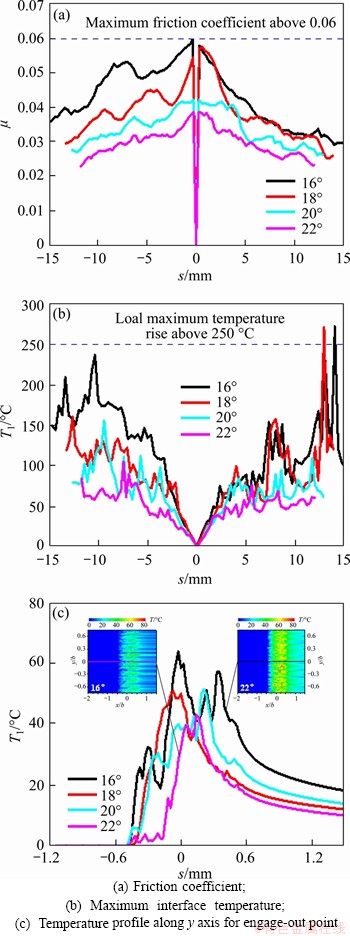
Figure 10 Pressure angle effects on friction-temperature performance of timing gear 4-6:

2) The effect of different machined roughness has been discussed, which shows that the shaved surfaces result in the larger areas of high temperature and higher friction coefficient. The polished surfaces yield smaller areas of high temperature and lower fiction.

Figure 11 Effect of gear modulus on interfacial friction and temperature rise for marine gear pair 4-6:

3) The influences of operating conditions on the friction-temperature performance are investigated. With the decrease of the input power and the reduction of the speed, the friction and interfacial temperature decrease clearly.

4) The influences of gear design parameters on the interfacial friction and temperature are studied through cases analyzed. The results indicate that increasing the pressure angle and the modulus may lead to the significant reductions of the interfacial friction and temperature.

Contributors

SHI Xiu-jiang, ZHAO Bin and ZHU Dong provided the concept and edited the draft of manuscript. SUN Wen, TONG Qing-shun and MA Xuan conducted the literature review and wrote the first draft of the manuscript. LU Xi-qun and HE Tao edited the draft of manuscript.

Conflict of interest

SHI Xiu-jiang, LU Xi-qun, HE Tao, SUN Wen, TONG Qing-shun, MA Xuan, ZHAO Bin and ZHU Dong declare that they have no conflict of interest.

References

[1] ZHU D, CHENG H S. An analysis and computational procedure for EHL film thickness, friction and flash temperature in line and point contacts [J]. Tribology Transactions, 1989, 32(3): 364-370.

[2] ZHU D, HU Y Z. A computer program package for the prediction of EHL and mixed lubrication characteristics, friction, subsurface stresses and flash temperatures based on measured 3-D surface roughness [J]. Tribology Transactions, 2001, 44(3): 383-390.

[3] KUMAR P, JAIN S C, RAY S. Thermal EHL of rough rolling/sliding line contacts using a mixture of two fluids at dynamic loads [J]. Journal of Tribology, 2002, 124(4): 709-715.

[4] KUMAR P, KHONSARI M M. Combined effects of shear thinning and viscous heating on EHL characteristics of rolling/sliding line contacts [J]. Journal of Tribology, 2008, 130(4): 041505.

[5] ZHANG X, KANAPATHIPILLAI S, WU T, PENG Z X. Frictional behaviour and friction mechanisms of rolling-sliding contact in mixed EHL [J]. Tribology International, 2017, 114: 201-207. DOI:10.1016/j.triboint.2017.04.032.

[6] SIMON V. Influence of position errors on EHD lubrication in spiral bevel gears [C]// International Joint Tribology Conference. 2010: 179-181.

[7] SIMON V. Improvements in the mixed elastohydrodynamic lubrication and in the efficiency of hypoid gears [J]. Journal of Engineering Tribology, 2020, 234(6): 795-810. DOI: 10.1177/1350650119866027.

[8] WANG X, LIU W, ZHOU F, ZHU D. Preliminary investigation of the effect of dimple size on friction in line contacts [J]. Tribology International, 2009, 42(7): 1118-1123.

[9] MASJEDI M, KHONSARI M M. Theoretical and experimental investigation of traction coefficient in line-contact EHL of rough surfaces [J]. Tribology International, 2014, 70: 179-189.

[10] HARTINGER M, REDDYHOFF T. CFD modeling compared to temperature and friction measurements of an EHL line contact [J]. Tribology International, 2018, 126: 144-152. DOI: 10.1016/j.triboint.2018.05.012.

[11] EBNER M, YILMAZ M, LOHNER T, MICHAELIS K, HOHN B R, STAHL K. On the effect of starved lubrication on elastohydrodynamic (EHL) line contacts [J]. Tribology International, 2018, 118: 515-523. DOI: 10.1016/j.triboint. 2017.06.004.

[12] WU S, CHENG H S. A friction model of partial-EHL contacts and its application to power loss in spur gears [J]. Tribology Transactions, 1991, 34(3): 398-407.

[13] HE S, CHO S, SINGH R. Prediction of dynamic friction forces in spur gears using alternate sliding friction formulations [J]. Journal of Sound and Vibration, 2008, 309(3-5): 843-851.

[14] AKBARZADEH S, KHONSARI M M. Thermoelastohydrodynamic analysis of spur gears with consideration of surface roughness [J]. Tribology Letters, 2008, 32(2): 129-141.

[15] LIU H J, LIU H L, ZHU C C, WEI P T, TANG J Y. Tribological behavior of coated spur gear pairs with tooth surface roughness [J]. Friction, 2018, 7(2): 117-128. DOI:10.1007/s40544-017-0193-3.

[16] LI S, KAHRAMAN A. A tribo-dynamic model of a spur gear pair [J]. Journal of Sound and Vibration, 2013, 332(20): 4963-4978.

[17] REN N, ZHU D, CHEN W W, LIU Y, WANG Q J. A three-dimensional deterministic model for rough surface line-contact EHL problems [J]. Journal of Tribology, 2009, 131(1): 011501.

[18] ZHU D, REN N, WANG Q J. Pitting life prediction based on a 3D line contact mixed EHL analysis and subsurface von Mises stress calculation [J]. Journal of Tribology, 2009, 131(4): 041501.

[19] HE T, WANG J X, WANG Z J, ZHU D. Simulation of plasto-elastohydrodynamic lubrication in line contacts of infinite and finite length [J]. Journal of Tribology, 2015, 137: 041505.

[20] SHI X, SUN W, LU X, MA X, ZHU D, LU X, ZHAO B, HE T. Three-dimensional mixed lubrication analysis of spur gears with machined roughness [J]. Tribology International, 2019, 140: 105864. DOI: 10.1016/ j.triboint.2019.105864.

[21] DOWSON D, HIGGINSON G R. Elastohydrodynamic lubrication [M]. New York: Pergamon Press, 1977.

[22] ROELANDS C J A. Correlation aspects of viscosity-temperature-pressure relationship of lubricating oils [D]. Netherlands: Delft University of Technology, 1966.

[23] BAIR S, WINER W O. A rheological model for elastohydrodynamic contacts based on primary laboratory data [J]. Journal of Tribology, 1979, 101(3): 258-264.

[24] HE T, ZHU D, WANG J, WANG Q. Experimental and numerical investigations of the stribeck curves for lubricated counterformal contacts [J]. Journal of Tribology, 2017, 139: 021515. DOI: 10.1115/1.4034051.

[25] HE T, ZHU D, WANG J, WANG Q. Experimental and numerical investigations of the stribeck curves for lubricated counterformal contacts [J]. Journal of Tribology, 2017, 139: 021515. DOI: 10.1115/1.4034051.

(Edited by FANG Jing-hua)

中文导读

船用齿轮基于三维线接触混合润滑模型摩擦以及闪温预测

摘要：船舶传动齿轮由于啮合过程中齿面摩擦大、温度高，经常发生磨损和胶合故障。本文基于线接触的三维混合润滑模型，建立了一种预测船用定时齿轮在一个啮合周期内的瞬态摩擦温度特性的数值解法，并与Blok理论进行了对比，验证了该方法的正确性。研究了表面粗糙度对润滑特性的影响，对几种典型齿轮副进行研究，结果表明，由于较严重的表面粗糙接触，齿轮副4-6的摩擦因数最大，界面温度最高，而抛光齿轮表面的摩擦因数最小，界面温度最低。此外，讨论了工况和结构对摩擦温度状态的影响，研究表明在重载、低速的工况会导致摩擦因数较大以及温度较高的问题。同时，通过对齿轮模数和压力角等结构设计参数的优化，可以显著提高齿轮的界面摩擦和温度性能。

关键词：齿轮；三维线接触；混合润滑；表面粗糙度；摩擦；闪温

Foundation item: Project(51905118) supported by the National Natural Science Foundation of China; Project(3072020CF0306) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2020-05-18; Accepted date: 2020-10-27

Corresponding author: LU Xi-qun, PhD, Professor; Tel: +86-18645066370; E-mail: luxiqun@hrbeu.edu.cn; ORCID: https://orcid.org/ 0000-0001-7198-9117; HE Tao, PhD, Associate Professor; Tel: +86-13540669661; E-mail: hetao633@foxmail.com; ORCID: https://orcid.org/0000-0003-2278-980X