J. Cent. South Univ. (2017) 24: 1817-1825
DOI: https://doi.org/10.1007/s11771-017-3590-x
Improving cam profile design optimization based on classical splines and dynamic model
XIA Bi-zhong(夏必忠), LIU Xin-cheng(刘新成), SHANG Xin(尚欣), REN Shi-yuan(任世远)
Department of Advanced Manufacturing, Shenzhen Graduate School of Tsinghua University, Shenzhen 518055, China
 Central South University Press and Springer-Verlag GmbH Germany 2017
Central South University Press and Springer-Verlag GmbH Germany 2017
Abstract: Cam profiles play an important part in the performance of cam mechanisms. Syntheses of cam profile designs and dynamics of cam designs are studied at first. Then, a cam profile design optimization model based on the six order classical spline and single DOF (degree of freedom) dynamic model of single-dwell cam mechanisms is developed. And dynamic constraints such as jumps and vibrations of followers are considered. This optimization model, with many advantages such as universalities of applications, conveniences to operations and good performances in improving kinematic and dynamic properties of cam mechanisms, is good except for the discontinuity of jerks at the end knots of cam profiles which will cause vibrations of cam systems. However, the optimization is improved by combining the six order classical spline with general polynomial spline which is the so-called “trade-offs”. Finally, improved optimization is proven to have a better performance in designing cam profiles.
Key words: cam profile design; spline; optimization; trade-off
1 Introduction
Cam mechanisms have been widely applied to automated machine because of the simplicity, compactness and versatility of its structure and motion. Design of cam profiles which play an important part in the performance of cam mechanisms is an essential and critical step for designing cam mechanisms. Development tendency of high speed, high precision and high efficiency for cam mechanisms demands that cam profiles meet not only the requirements of kinematics but also that of dynamics. In order to design a cam profile with good dynamic properties, FLOCKER [1-3] has presented two closed-form cam profiles for single-dwell and multiple-dwell cam mechanisms, and the positive and negative acceleration can be easily set through adjusting parameters of profiles. HSIEH [4] proposed a systematic method for the design and analysis of cam profiles using three circular-arc curves with kinematic properties considered. LIANG and HUANG [5] proposed a command smoothing technique to design cam profiles for reducing vibrations of a high speed cam mechanism by combining command smoother and original cam profiles. According to the geometries and relationships of instant velocity centers, SHIN et al [6] have derived coordinates of cam profiles and have given an automatic program for breadth cam profiles. ACHARYYA and NASKAR [7] studied the fractional polynomial modified trapezoid cam profile in which polynomial exponents of cam profiles are no longer limited to integers but extended to real numbers. Because of the flexibility, versatility and being applied to optimization models easily, splines have been frequently applied to designing cam profiles in recent years. Many articles about synthesizing cam profiles using splines have been published. NORTON [8] has detailed applications of various splines (include classical splines, B-splines, Bezier curves, Hermite splines, Shumaker quadratic splines etc.) in designing cam profiles with examples. A synthesis method of flexible cam profiles based on smoothing curves has been proposed by NGUYEN and KIM [9], which allows designers to refine the cam motion by local modifications under discrete constraints. CHAVAN and JOSHI [10] have synthesized a type of cam profile using classical splines in which expected dynamic characteristics can be obtained by adjusting locations of knots. And the article has discussed the effects of follower displacement at knots on the performance of cam mechanisms, however, the effects of angular positions at knots are not considered.
Being applied to optimization models easily is a significant advantage for splines and many articles about cam profile optimizations are based on splines. QIU et al [11] proposed a universal multi-objective optimal approach about cam profiles based on B-splines, which is able to deal with multiple objective problems and compute weighting coefficients automatically according to the priority of constraint conditions. NASKAR et al [12] and MANDAL et al [13] studied cam profile syntheses and optimizations using classical splines and B-splines. And they took accelerations and jerks as objective functions, using knot positions as design variables, however, the inadequacy of which is that it has considered kinematic parameters while dynamic parameters (such as vibrations, jumps and wear) are not included. Problems about minimizing and restricting vibrations of cam mechanisms over a range of speeds have been investigated by JIANG et al [14, 15] based on Hermite splines and non-uniform B-splines.
In this work, a lot of syntheses of cam profile designs and dynamics of cam designs are introduced. And the six order classical spline and single DOF dynamic model of a single-dwell cam mechanism are introduced. Then, a cam profile design optimization model using the six order classical spline based on a specific single-dwell cam mechanism is developed. In addition, dynamic constraints such as jumps and vibrations of the follower are considered in the optimization model. This optimization model is good and has many advantages such as universalities of applications, conveniences to operations and good performances in improving kinematic, dynamic properties of cam mechanisms except for the discontinuity of jerks at the end knots of cam profiles which will cause vibrations of cam systems. However, the optimization is improved by combining the six order classical spline with general polynomial spline which is called “trade-offs”.
2 Classical splines and single DOF dynamic model of cam mechanism
2.1 Classical splines
Classical spline is a kind of curve made up of polynomial pieces that are blended together at the ends (called knots) [8]. In designing cam profiles, the six order classical spline is one of the most frequently used. Therefore, the six order classical spline will be used as an example to introduce classical splines. A cam- displacement curve described by classical splines is shown in Fig. 1. Suppose there are k knots and k-1 polynomial pieces, positions of the knots are set as follows:
Angle positions of the knots: θ1≤θ2≤…≤θk-1≤θk.
Follower displacements at the knots: s1, s2, …, sk.
Cam displacements can be described as follows [8]:
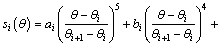

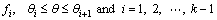 (1)
(1)
where ai, bi, …, fi are undetermined coefficients.
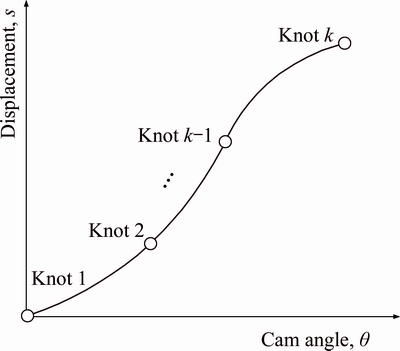
Fig. 1 Cam displacement
There are 6(k-1) unknown coefficients, so 6(k-1) equations are required for solutions. Firstly, follower displacements at the interior knots give k-2 simple equations called interpolation equations. They are expressed as follows:
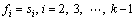 (2)
(2)
Secondly, the continuity of splines at the interior knots will provide 5(k-2) smoothness equations expressed as follows:
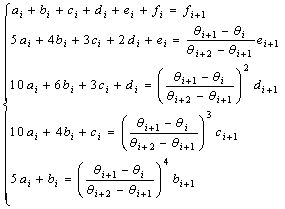
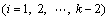 (3)
(3)
Remaining six equations are provided by kinematic parameters of the end knots called boundary condition equations. They are expressed as follows:
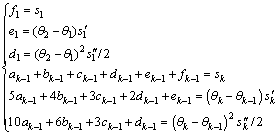 (4)
(4)
Unknown coefficients of the cam displacement can be solved based on Eqs. (2), (3) and (4). From Eq. (4), it can be found that splines of six orders can ensure accelerations continuous at the end knots but the continuity of the jerk will not be guaranteed.
Jerk is one of the major causes about vibrations of mechanical systems. Therefore, if continuities of jerks at the end knots could not be guaranteed, required vibrations of the mechanical system will not be ensured. It seems that this problem can be solved easily by adopting splines of higher orders than six but in fact the higher-order spline is not appropriate because it is complicated and time-consuming. This problem will be solved by combining the six order classical spline with general polynomial spline.
2.2 Single DOF dynamic model of cam mechanism
The majority of cam mechanisms can be simplified to a single DOF dynamic model [11, 16-18] as shown in Fig. 2. With reference to Fig. 2, the dynamic equation can be written as follows by applying Newton’s second law of motion to the system:
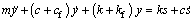 (5)
(5)
where m is equivalent mass of the follower system; k and c are equivalent stiffness and damping of the follower system; kf and cf are stiffness coefficient and damping coefficient of the return spring. From Eq. (5), the cam displacement s (the cam profile) can be seen as an input excitation of the follower system. For a structure determined cam mechanism, cam profile determines the responses of follower system.
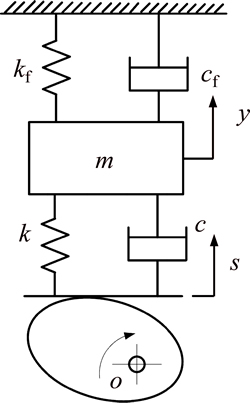
Fig. 2 Single DOF dynamic model of cam mechanism
3 Primary optimization of cam profile design
3.1 Primary optimization model
A primary optimization model of a single-dwell cam profile design based on the six order classical spline and single DOF dynamic model will be established, which is the foundation of improved optimization.
Larger contact forces which will aggravate wear of cam surface are never expected. And the maximum value of contact forces is always wanted as small as possible. Therefore, the maximum contact force will be chosen as objective function in this work. As to vibrations of the follower, in many cases they are required to be less than a specified value merely [15]. Schematic diagram of the single-dwell cam displacement described by classical splines is shown in Fig. 3. Cam displacement is set at seven knots composed of six polynomial curves. Positions of the knots are set as symmetrical. What’s more, knots 1, 4 and 7 are fixed knots. Since positions of knots are symmetrical, once positions of knots 2 and 3 are established, locations of knots 5 and 6 are also determined. So the positions of knots 2 and 3 are chosen as design variables. Design variables can be expressed by a vector as follows:
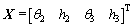 (6)
(6)
where θ2 and θ3 are cam angular positions of knots 2 and 3 while h2 and h3 are the corresponding follower displacements.
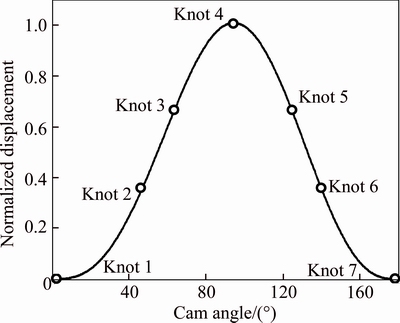
Fig. 3 Cam displacement of single-dwell cam mechanism
According to the dynamic Eq. (5), objective contact force can be expressed as follows:
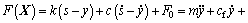
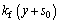 (7)
(7)
where F0 is the initial contact force, and F0=kf·s0.
The primary optimization model is expressed as
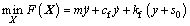

Subject to
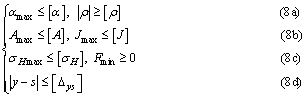
Constraints of the optimization model can be divided into geometric constraints, kinematic constraints and dynamic constraints. Inequalities (8a) are geometric constraints to limit pressure angles and minimum radiuses of curvature of the cam profile; inequalities (8b) are kinematic constraints to restrict maximum accelerations and jerks of the cam profile; inequalities (8c) and (8d) are dynamic constrains. Besides, the former inequality of (8c) is to limit contact stresses and the latter is to avoid follower jumps; inequality (8d) is used to restrict displacement deviations caused by vibrations.
The genetic algorithm (GA) is selected to search optimum solutions of the optimization problems. GA is a method to search optimal solutions by simulating processes of natural evolution which is efficient in searching a highly non-linear multi-dimensional space. Searches of GA start from a set of candidate individuals called population, which can effectively avoid falling into a local optimal solution. LAMPINEN [19], WANG and UZSOY [20], and LI et al [21] have detailed the applications of GA in optimization.
3.2 Optimization results of a specific example
Associated model parameters of the specific single-dwell cam are shown in Table 1. Initial values of the design variables are chosen as X=[π/4 2 π/3 5]T. Optimization results of the single-dwell cam mechanism are presented in Figs. 4, 5, 6 and 7. By comparison, corresponding parametric curves of the initial cam profile and the cycloid cam profile are also shown in the figures. Optimal solution of the optimization model is X=[0.269 0.141 0.401 0.477] T.
Table 1 Model parameters of single-dwell cam mechanism
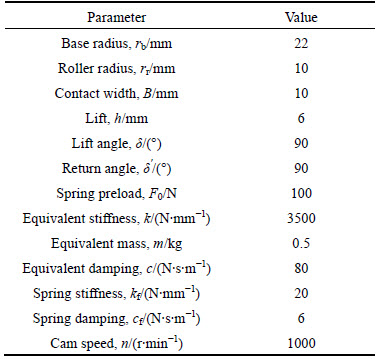
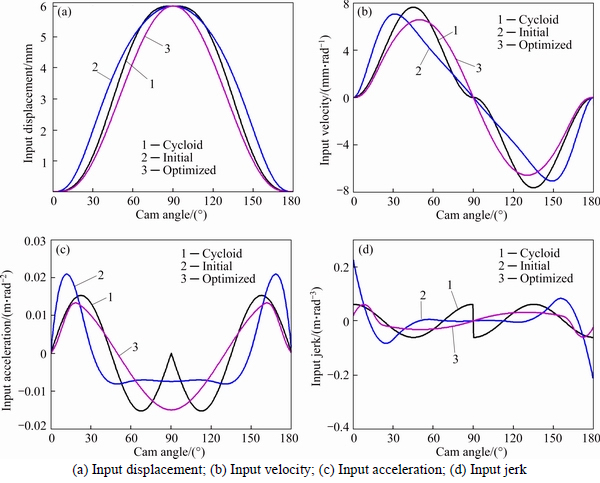
Fig. 4 Kinematic parameters of cam profile:
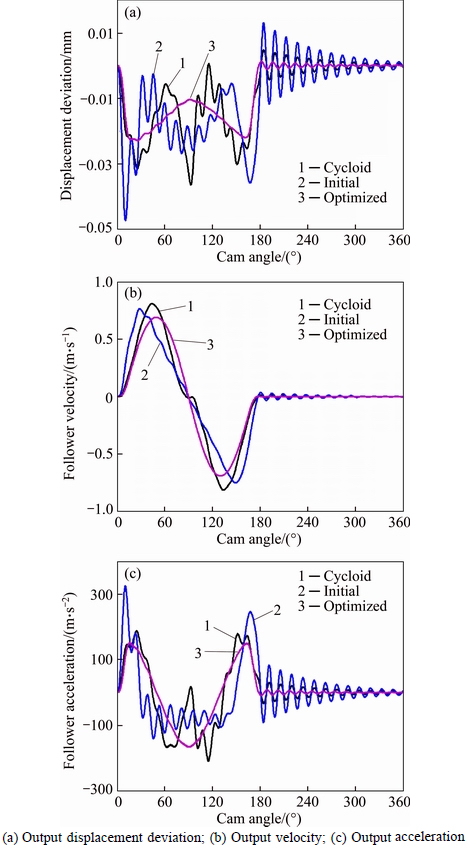
Fig. 5 Output kinematic parameters of follower system:
Figure 4 shows the displacements, velocities, accelerations and jerks of cam profiles, from which it can found that optimized profile is much gentler than cycloid profile and initial profile, which means less fluctuations and vibrations. Parameters shown in Fig. 5 are kinematic parameters of the follower system which are output results of the system under many conditions such as input excitations, characteristics of the cam mechanism and external factors. And it is not hard to find that optimized profile has a better performance than the other two profiles in kinematics.
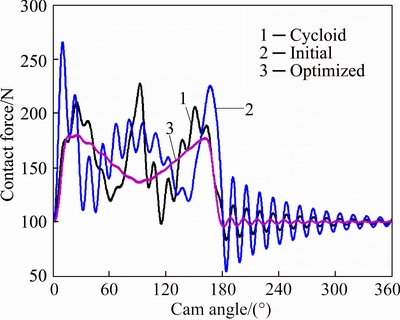
Fig. 6 Cam-follower contact forces
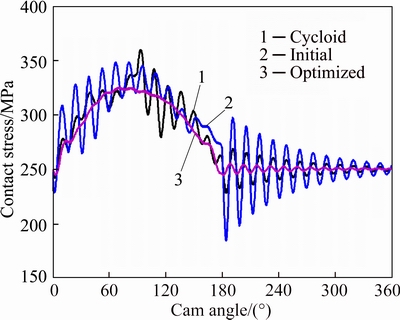
Fig. 7 Cam-follower contact stresses
Figures 6 and 7 show contact forces and contact stresses between the cam and follower from which it can be found that maximum contact force and contact stress of the optimized profile have obviously reduced compared with that of the cycloid profile and the initial profile. Furthermore, fluctuations of contact forces and contact stresses of the optimized cam profile are also the smallest. What’s more, output kinematic parameters of the follower system such as maximum velocities, maximum positive accelerations and maximum displacement deviations of the optimized profile are the smallest, whether the system is on primary vibration stage or on residual vibration stage. Although negative acceleration is larger than the positive one, cam and follower don’t separate because of the return spring force. In addition, contact forces and contact stresses have decreased due to the negative acceleration. The only disadvantage of optimized profile is the discontinuity of input jerks at the end knots which will be discussed and solved in next section. A detailed comparison of the three cam profiles is given in Table 2.
4 Improved optimization of cam profile design based on primary one
Jerk of the optimized cam profile is discontinuous at the end knots, which is determined by the deficiency of the six order classical spline. From Eq. (4), it is known that the six order classical spline has six boundary conditions and can only guarantee the continuity of accelerations. To get a jerk-continuous cam profile, the classical spline of higher orders than six has been tried. However, the higher the order of splines is, the more complex the cam profile expressions are, which are difficult to solve. Therefore, an improved optimization of the cam profile design, which is called “trade-offs”, is developed based on the primary one by combining the six order classical spline with general polynomial spline.
Compared with classical splines, general polynomial splines do not insist that spline functions interpolate given values at the knots. Furthermore, smoothness at each interior knot may be different for general polynomial splines. And boundary conditions do not have to be specified. The only requirement is that numbers of equations must equal numbers of the unknown coefficients [4]. From smoothness equation of the six order classical spline, it can be found that interior knots are continuous on the fourth order derivative but it is no sense since jerk (the third order derivative) is discontinuous at the end knots. Therefore, two jerk constraints of the end knots can be used to replace continuous equations of two interior knots on the fourth order derivative in order to get a cam profile with continuous jerk. The above is what the so-called “trade-offs” means.
It is known that knots 5 and 6 are determined by knots 2 and 3 so two knots from the remaining interior knots can be chosen as the replaced. And in this work knots 2 and 4 are chosen. Therefore, modified equations of the six order classical spline combined with general polynomial splines are expressed as follows:
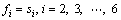 (9)
(9)

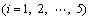 (10)
(10)
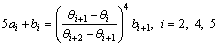 (11)
(11)
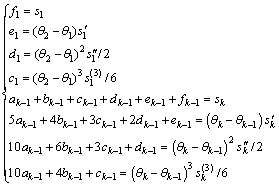 (12)
(12)
Objective functions and constraints are the same as the third chapter, and optimization results are shown in Figs. 8, 9, 10 and 11. Optimal solution is X=[0.356 0.253 1.047 3.902] T. Kinematic parameters of the cam profile are shown in Fig. 8; kinematic parameters of the follower system are shown in Fig. 9; dynamic parameters of the cam mechanism are shown in Figs. 10 and 11.
In Figs. 8-11, Optimization 1 means optimization results of the primary model, and Optimization 2 means optimization results of the improved one. From Figs. 8 and 9, it can be seen that maximum velocities, accelerations and displacement deviations of primary vibration about Optimization 2 are larger than those of Optimization 1, but not much. What’s more, the above does not have a large impact on dynamic properties of the cam mechanism. And it can be found that maximum values of contact forces and vibrations about Optimization 2 have declined more or less compared to the results of Optimization 1 from Figs. 10 and 11.
Table 2 Maximum value of kinematic and dynamic parameters


Fig. 8 Kinematic parameters of cam profile:
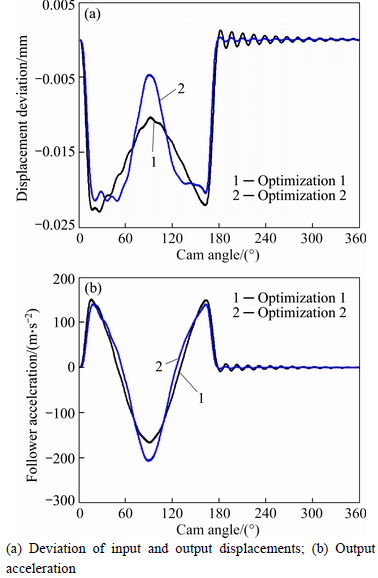
Fig. 9 Output kinematic parameters of follower system:

Fig. 10 Cam-follower contact forces

Fig. 11 Cam-follower contact stresses
Actually, the biggest advantage of Optimization 2 is that parameter curve fluctuations and residual vibrations are much smaller than those of Optimization 1. As shown in Fig. 8(d), jerk curve of Optimization 2 is continuous. Therefore, if the cam profile has a higher requirement about residual vibrations Optimization 2 is a better choice. Another advantage of Optimization 2 is that it is more flexible in dealing with cam profile problems about kinematic constraints and boundary conditions.
5 Conclusions
It is found that designing cam profiles is very interesting, which plays an important role in the performance of cam mechanisms. After studying a lot of syntheses of cam profile designs and dynamics of cam design, it can be found that the six order classical spline is one of the most frequently used splines in designing cam profiles.
Primary optimization developed using the six order classical spline based on a specific single-dwell cam mechanism is proven to have a good performance in improving kinematic and dynamic properties of cam mechanisms. Unfortunately, jerk curve of the cam profile at the end knots in this optimization is not continuous, which will cause vibrations of systems, because of the deficiency of the six order classical spline. However, improved optimization developed by combining the six order classical spline with general polynomial spline has compensated this defect effectively. And the so-called “trade-offs” is proven to have a better performance in designing cam profiles.
Appendix
The definition of cam mechanism pressure angle is that the acute angle between the positive pressure direction of the cam-follower contact point and the linear velocity direction of the force point of the follower. With reference to Fig. A1, the cam mechanism pressure angle is written as follows:
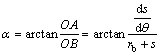 (A1)
(A1)
where rb is the base circle radius of the cam; s is the displacement of the follower; θ is cam rotation angle.
The radius of curvature of the theoretical cam profile is expressed as [4]
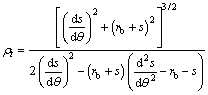 (A2)
(A2)

Fig. A1 Schematic of cam mechanism
The radius of curvature of the cam profile can be calculated by
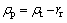 (A3)
(A3)
where rr is the radius of the roller.
The contact between the cam and roller can be regard as the contact between two cylinders, similarly. And the maximum contact stress of the contact area is written as follows:
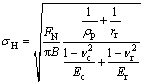 (A4)
(A4)
where FN is the positive pressure between the cam and roller; B is the contact width of the cam and roller; νc and νr are Poisson ratios of the cam and roller; Ec and Er are elastic moduli of the cam and roller.
References
[1] FLOCKER F W. A versatile acceleration-based cam profile for single-dwell applications requiring cam-follower clearance during dwell [J]. Journal of Mechanical Design, 2012, 134(8): 084505- 084505-7.
[2] FLOCKER F W. A versatile cam profile for controlling interface force in multiple-dwell cam-follower systems [J]. Journal of Mechanical Design, 2012, 134(9): 081002-081002-8.
[3] FLOCKER F W. Addressing cam wear and follower jump in single-dwell cam-follower systems with an adjustable modified trapezoidal acceleration cam profile [J]. Journal of Engineering for Gas Turbines and Power (Transactions of the ASME), 2009, 131(3): 327-335.
[4] HSIEH J. Design and analysis of cams with three circular-arc profiles [J]. Mechanism and Machine Theory, 2010, 45(6): 955-965.
[5] LIANG Zan, HUANG Jie. Design of high-speed cam profiles for vibration reduction using command smoothing technique [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2014, 228(18): 3322-3328.
[6] SHIN J H, LI Lin, YANG H D, KWON S M. Kinematical system of breadth cam profile design [J]. Journal of Central South University of Technology, 2011, 18(2): 451-457.
[7] ACHARYYA S, NASKAR T K. Fractional polynomial mod traps for optimization of jerk and hertzian contact stress in cam surface [J]. Computers & Structures, 2008, 86(3): 322-329.
[8] NORTON R L. Cam Design and Manufacturing Handbook [M]. New York: Industrial Press, 2009: 186-205.
[9] NGUYEN V T, KIM D J. Flexible cam profile synthesis method using smoothing spline curves [J]. Mechanism and Machine Theory, 2007, 42(7): 825-838.
[10] CHAVAN U, JOSHI S. Synthesis of cam profile using classical splines and the effect of knot locations on the acceleration, jump, and contact force of cam follower system [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2011, 225(12): 3019-3030.
[11] QIU Hua, LIN Chang-jun, LI Zi-ye, HIROAKI O, Wang Jian, YUE Yong. A universal optimal approach to cam curve design and its applications [J]. Mechanism & Machine Theory, 2005, 40(6): 669-692.
[12] NASKAR T K, MISHRA R. Introduction of control points in B-splines for synthesis of ping finite optimized cam motion program [J]. Journal of Mechanical Science & Technology, 2012, 26(2): 489-494.
[13] MANDAL M, NASKAR T K. Introduction of control points in splines for synthesis of optimized cam motion program [J]. Mechanism & Machine Theory, 2009, 44(1):255-271.
[14] JIANG J K, IWAI Y R, SU H. Minimizing and restricting vibrations in high-speed cam-follower systems over a range of speeds [J]. Journal of Applied Mechanics, 2007, 74(6): 1157-1164.
[15] JIANG J K, IWAI Y R. Improving the b-spline method of dynamically compensated cam design by minimizing or restricting vibrations in high-speed cam-follower systems [J]. Journal of Mechanical Design, 2009, 131(4): 041003-041003-8.
[16] XIA Bi-zhong, REN Shi-yuan, SHANG Xin, LIU Xin-cheng. Dynamic analysis and optimization of cutting mechanism about aluminum electrolytic capacitor casing machine [J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2015, doi: http://dx.doi.org/10.1177/ 1464419315611770
[17] FABIEN B C. The design of dwell-rise-dwell cams with reduced sensitivity to parameter variation [J]. Journal of the Franklin Institute, 1995, 332(2): 195-209.
[18] YILMAZ Y, KOCABAS H. The vibration of disc cam mechanism [J]. Mechanism and Machine Theory, 1995, 30(5): 695-703.
[19] LAMPINEN J. Cam shape optimisation by genetic algorithm [J]. Computer-Aided Design, 2003, 35(8): 727-737.
[20] WANG Cheng-shuo, UZSOY R. A genetic algorithm to minimize maximum lateness on a batch processing machine [J]. Computers and Operations Research, 2002, 29(12): 1621-1640.
[21] LI Yun, LIU Gang, LAO Song-yang. A genetic algorithm for community detection in complex networks [J]. Journal of Central South University, 2013, 20(5): 1269-1276.
(Edited by YANG Bing)
Cite this article as: XIA Bi-zhong, LIU Xin-cheng, SHANG Xin, REN Shi-yuan. Improving cam profile design optimization based on classical splines and dynamic model [J]. Journal of Central South University, 2017, 24(8): 1817-1825. DOI: https://doi.org/10.1007/s11771-017-3590-x.
Received date: 2015-12-16; Accepted date: 2016-08-30
Corresponding author: SHANG Xin, PhD; Tel: +86-13066881363; E-mail: shangxin0375@126.com