文章编号:1004-0609(2016)-03-0655-11
相干度分析用于强干扰背景下多频激电信号处理
刘卫强1, 2,陈儒军1, 2
(1. 中南大学 地球科学与信息物理学院,长沙 410083;
2. 中南大学 有色金属成矿预测教育部重点实验室,长沙 410083)
摘 要:提出将相关度分析用于强噪声环境下的m序列多频激电信号处理。多频激电各周期电压电流数据的相关度与数据观测质量、信噪比存在明显的对应关系。当相关系数在0.5以上时,数据信噪比较高,可用于后续数据处理与复电阻率计算;而当相关系数在0.5以下甚至接近于0时,信噪比很低,有用信号已基本被噪声淹没,无法用于后续数据处理。将相关度分析应用于甘肃白银矿区实测数据,设置阈值提取出质量较高的观测数据用于后续数据处理,从而获得更为准确的复电阻率计算结果。对于干扰特别严重的测点,可使复电阻率相位误差由1000 mrad以上降至150 mrad以下,高频相位误差降至40 mrad以下。幅值误差由100%以上降至10%以下,应用效果较好。
关键词:m序列多频激电;噪声压制;复电阻率;相关度;阈值
中图分类号:P631 文献标志码:A
激电法是一种有效应用于金属矿产资源勘查的物探方法[1-4]。自20世纪50年代出现频率域激电观测方法以来,先后产生了变频法[5]、奇次谐波法[6]、相位激电法[7],双频激电法[8-9]、伪随机多频激电法[10-12]等多种方法。各种频率域激电法基本原理一致,主要区别在于发送电流和观测方式的不同。从而也决定了测量信息是否丰富、野外工作是否方便、仪器设备是否轻便、抗干扰能力是否足够等问题。m序列多频激电法是在何继善院士提出的伪随机信号电法基础上发展的一种有效的矿产资源勘查方法[13]。m序列与2n序列类似,都属于伪随机序列,具有宽频谱特性,可以实现一次发射,同时,获得多个频点的复电阻率信息。2n序列能量主要分布在呈均匀对数间隔的频点上,m序列能量主要分布在呈线性间隔的频点上[14-15]。国防科技大学信息地球物理协同创新中心和湖南强军科技有限公司利用自主研发的多频激电系统在藏南罗布莎矿区,探测到了价值数十亿元人民币的铬铁矿,取得了良好勘探效果[13, 16]。
多频激电法的工作方式与直流电法相同。都是利用接地电极来测量电位差,很容易受到各种人文、自然噪声等干扰,当在生产矿山周边进行激电法勘探时,噪声干扰更加严重[17]。主要噪声来源包括人类活动、大地电流、工业游散电流、天电干扰、高压电力线等。如果在数据预处理阶段未能对噪声进行有效压制,会使后期的复电阻率计算产生重大偏差,出现错误的结果。
长期以来,国内外传统的研究重心主要集中于电磁耦合干扰的去除。对于电磁耦合之外的强噪声压制,目前的研究热点是利用伪随机信号良好的自相关、互相关特性进行大地系统辨识并压制随机噪声[18-20]。英国PGS公司的MTEM多道瞬变电磁系统通过反卷积运算提取大地系统响应,有一定的降噪效果。它需要在发送机周围采用相同的接收机测量未经过大地的观测系统本身的冲击响应[21]。近年来,国内重点研究的基于系统辨识的伪随机信号电法,是一种全新的勘探方法,有别于传统的“时间域”和“频率域”观测模式。理论上既能高效率获取大地的时间响应和频谱信息,又有很强的压制噪声干扰的能力,应用前景广阔[22]。但要求伪随机序列的码元足够窄、阶数足够高,激励电流波形不能失真。基于系统辨识的伪随机信号电法仪在野外勘查中的应用仍处在进一步推广与完善中。
对于频谱激电法,在野外勘探中常用的噪声压制最常用的方法为数字滤波器[23-25]和周期叠加[26-28]。基于离散傅里叶变换(DFT)的数字滤波在各种激电观测系统中都有广泛应用,通过设置高通、低通、带通、陷波、梳状等滤波器可对观测数据中的噪声进行压制。但是野外干扰往往表现为多种类型噪声的叠加,其频谱分布范围广泛,与多频激电信号频谱相互重叠,从而使数字滤波器变得无能为力。周期叠加主要针对幅值类似于高斯分布的随机噪声。当环境中有少量强噪声出现时,可以通过延长观测时间,增大叠加次数来对其进行压制。但是周期叠加本身并不能对各周期观测数据质量进行评价。当环境干扰严重,强噪声在在大部分观测周期持续出现时,周期均值叠加不再有效。基于Robust方法的稳健周期叠加可以对尖峰脉冲噪声进行压制,一定程度上降低计算误差,提高数据质量[29]。但Robust叠加要求叠加数据中离群值的比例不能高于50%,对于干扰特别严重的测点,仍不足以充分压制干扰。另外平滑滤波和小波分析也被用于激电叠后数据的噪声压制[24, 27]。但是,当噪声干扰严重时,基于叠后数据的处理方法都不可避免地会带来激电信息的损失。
虽然不同的地球物理方法具有不同的观测方式与信号特征。但是不同地球物理方法遭遇的噪声干扰具有一定共性。所以,一些已经有效应用于电磁法及地震勘探的噪声压制方法可以为频谱激电数据处理提供参考。本文作者提出相关度分析的方法来从干扰严重的原始数据中提取出质量较高的数据,从而提高复电阻率计算精度。相关度分析在大地电磁[30-31]与地震资料处理[32]中有广泛应用,在电阻率法和激电法中尚未直接应用。对于噪声干扰严重的多周期观测数据,虽然整体数据质量较差,但并非所有周期的数据都受到严重的噪声干扰。计算各周期激电电压、电流数据之间的相关度,相关度与实测电压数据的数据质量直接相关,根据相关系数分布范围,设置阈值进行滤波,可在强噪声干扰环境下提取出质量较高的观测数据,利用高品质数据进行Robust周期叠加与后续数据处理,可以获得更为准确的复电阻率计算结果。本文作者结合甘肃白银地区实测多频激电数据证明该方法的有效性。
1 相关度分析处理方法基本原理
相关度分析在大地电磁[30-31]和地震资料处理[32]中有广泛应用。但在电阻率法和激电法中尚无直接利用。在大地电磁中可以用电场信号与磁场信号的相关度来衡量大地电磁信号的信噪比。一般信噪比越高,相关度越趋近于1。在地震资料处理中,可以用各地震道之间的相关系数来分析道间相似程度,求取静校正时移量。本文作者将相关度分析用于强噪声环境下的多频激电数据处理。对于噪声干扰严重的多周期观测数据,虽然整体数据质量较差,但并非所有周期的数据都受到严重的噪声干扰。只要原始观测数据中存在数据质量较高的周期,就可以通过分析相关度进行提取。选取高品质的观测数据进行后续计算,可以获得更为准确的复电阻率计算结果。相关度计算公式有很多种,本文作者选用皮尔逊相关度[33],其不受两组数据数量级不同的影响。对于序列xi和yi,其中i=1,2,…,n。相关度C的计算公式如下:
 (1)
(1)
式中: 、
、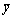 分别为序列xi和yi的均值。相关度分布为-1~1,0.5以上表明相关度较强,0.5以下表示相关度较弱,相关度0以下则表示负相关。对于多频激电法,同周期的电压数据与电流数据应该具有较强的相关性。对于不同测点,相关度分布范围主要受到不同测点信噪比、复电阻率幅值、相移等因素的影响。对同一测点,由于复电阻率幅值和相移基本稳定,不同周期所计算出的相关度,其变化范围主要是受不同观测时间段信噪比不同的影响。可以用相关度来衡量多频激电信号的信噪比。相关度越接近于1,信噪比越高,数据质量越好。相关度越接近于0,信噪比越低,数据质量越差。
分别为序列xi和yi的均值。相关度分布为-1~1,0.5以上表明相关度较强,0.5以下表示相关度较弱,相关度0以下则表示负相关。对于多频激电法,同周期的电压数据与电流数据应该具有较强的相关性。对于不同测点,相关度分布范围主要受到不同测点信噪比、复电阻率幅值、相移等因素的影响。对同一测点,由于复电阻率幅值和相移基本稳定,不同周期所计算出的相关度,其变化范围主要是受不同观测时间段信噪比不同的影响。可以用相关度来衡量多频激电信号的信噪比。相关度越接近于1,信噪比越高,数据质量越好。相关度越接近于0,信噪比越低,数据质量越差。
通过分析同一测点不同观测周期之间的相关度分布范围,设置阈值进行滤波,可以提取出数据质量较高的原始数据,剔除数据质量较差的原始数据。然后利用信噪比较高的周期数据进行Robust周期叠加和后续数据处理,如此可以大大提高复电阻率计算结果的准确度。Robust周期叠加就是将稳健M估计用于 周期叠加[29, 34]。对于同一采样点在N个周期中的观测值Yn,n=1,…,N,其稳健估计值θ可以通过求解如下方程获得:
 (2)
(2)
式中:ψ称为影响函数,用来控制原始观测数据中离群值对最终结果的影响,σ称为尺度参数,用来表征需要降权的离差范围,θ称为位置参数表征Robust叠加结果。本研究中所用的影响函数为Hampel函数,其表达式如下[35]:
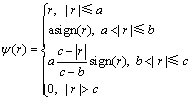 (3)
(3)
式中:a、b、c为调节常数,取a=1.2,b=3.5,c=8.0。sign(r)为符号函数。
Robust周期叠加相对于传统的均值叠加方法,可以进一步压制噪声,提高数据质量。相关度分析与Robust周期叠加相结合的方法可以克服原始数据中由噪声引起的离群值比例超过Robust方法崩溃点(50%)的情况,从而在最大程度上压制噪声,提高数据质量。经过相关度分析提取与Robust稳健叠加,最终得到信噪比较高的电压波形与电流波形,然后可以计算多个频点对应的复电阻率,复电阻率计算式如下:
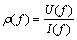 (4)
(4)
式中: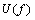 和
和 分别为电压、电流频谱,
分别为电压、电流频谱, 为复电阻率频谱。
为复电阻率频谱。
2 相关度分析在实际资料中的应用
2.1 甘肃白银测区m序列多频激电观测方法
湖南强军科技公司的85321A-SIP分布式激电仪采集站,采取大规模分布式同步采集激电数据。2014年在甘肃白银地区获得了多周期观测的多频激电实测数据。采样频率为64 Hz,发送电流为5阶m序列,每周期16 s,一个周期内含1024个采样点。每测点观测160周期,观测时间超过40 min。m序列时钟周期为0.5 s,供电电流幅值8A左右。发送电流波形及频谱如图1所示。
图1(a)所示为m序列多频频谱激电法发送电流时间域波形,图1 (b)所示为发送电流频谱。虽然多频激电信号的频谱比较丰富(0~32 Hz),但为了保证信号强度,只取复电阻率频谱在1/16 Hz~1 Hz范围内(前2~17个样点)的值。每4个点做一次平均,作为对应于0.16 Hz、0.41 Hz、0.66 Hz、0.91 Hz 4个频点的复电阻率计算结果。由复电阻率可以进一步计算视频散率、相对相位等激电参数。
测区位于正在生产的矿区周边,多种类型的强噪声持续出现。分别取该测区某测线Line.1的实测数据,进行分析处理。该测线采用中梯装置。AB=[-2200,2200] m,MN=20 m,测线上共有100个测点,点距为20 m,测线长为2 km。甘肃白银测区存在一个已初步探明的铅锌矿容矿断层,断层为东西走向,向南倾斜,测线Line.1 为南北走向,小号点在南。测线大致垂直于断层走向。在测线西面较远处有一个钻孔已经打到富矿体,测线东面附近约20 m处,另有一钻机正在施工打钻,带来较为严重的电磁干扰。侧线旁钻机施工如图2所示。
分别取测线Line.1上干扰严重的测点No.44和干扰相对较小的测点No.96的电压电流数据,分析其相关度与数据质量的对应关系。

图1 多频激电法发送电流波形及频谱
Fig. 1 Wave and frequency spectra of transmitting current in SSIP

图2 大功率钻机正在测线旁开钻
Fig. 2 Drilling machine near data acquisition station
2.2 各周期电流电压相关度与数据质量对应关系
首先分别计算测点No.96的160个周期的电压电流相关度,再分别利用各周期数据单独计算复电阻率。4个频点对应的复电阻率相位、幅值计算结果与相关度的对比关系如下图3所示。
测点No.96处干扰较小,数据整体信噪比较高,对该测点,各周期电压电流数据的相关度都在0.9以上。但由图3(a)和(b)仍可以看出,当电压电流的相关度有所降低时,复电阻率相位、幅值计算结果也会相应地发生偏差。相关度变化引起的相位偏差约为50 mrad 左右,幅值偏差约为50 Ω·m。由于测点No.96数据整体信噪比较高,而且异常值所占比例低于50%,因此,利用相关度分析剔除异常周期数据与利用全部周期数据进行计算,两种方法所得结果相差 不大。
对于测点No.44,噪声干扰相当严重,大部分周期信噪比很低。分别计算其160个周期的电压电流相关度,相关度分布范围为-0.3248~0.6678。再分别利用各周期数据单独计算复电阻率,4个频点对应的复电阻率相位、幅值计算结果与相关度的对比关系如图4所示。
由图4(a)和(b)可以看出,当电压电流的相关度降低时,复电阻率相位、幅值计算结果相应地发生偏差。由于该点信噪比很低,相关度变化范围也比较大,引起的相位偏差高达1000 mrad 以上,幅值偏差也在100 Ω·m以上。数据整体信噪比很低,而且仅在测量初期的约20个周期相关度较高,在0.5以上。为了对比不同相关度下的实测信号波形,分别提取相关度最大和相关度最小的两个周期的电压、电流波形,波形示意图5和6所示。
由图5(a)和6(a)可以看出,电流信号较稳定,信噪比较高。由图5(b)和6(b)可以看出,相关度越大,电压数据信噪比越高,数据质量越好。相关度越低,电压数据信噪比越低,数据质量越差。当相关系数在0.5以上时,数据信噪比较高,波形较好,可用于后续数据处理与复电阻率计算。而当相关系数在0.5以下甚至低于0时,信噪比很低,有用信号已基本被噪声淹没,无法用于后续数据处理。所以对干扰严重的测点No.44,设置相关度阈值为0.5,仅保留原始观测数据160个周期中相关度大于0.5的周期。再利用提取出的高品质数据进行周期叠加计算复电阻率。结果就会更加准确。

图3 测点No.96(距离约为1900 m)处各周期电压电流相关度及复电阻率计算结果
Fig. 3 Coherency of potential difference and current and complex resistivity of each period in survey point No.96 (Distance is about 1900 m)
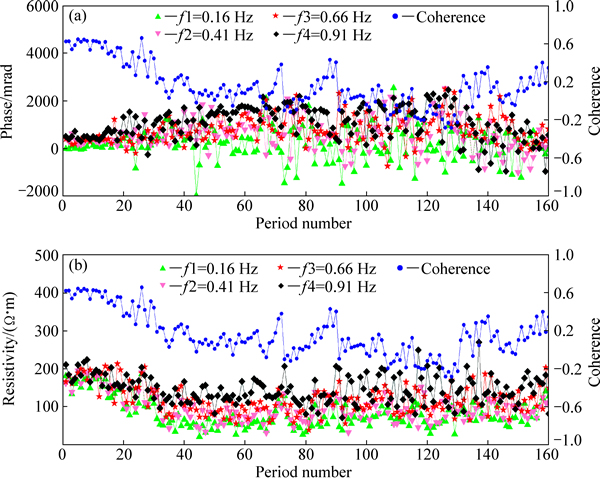
图4 测点No.44(距离约为860 m)处各周期电压电流相关度及复电阻率
Fig. 4 Coherency of potential difference and current and complex resistivity of each period in survey point No.44 (distance is about 860 m)

图5 测点No.44相关度最大的周期多频激电电流电压波形
Fig. 5 Current wave and potential difference wave of period at maximum coherency in survey point No.44
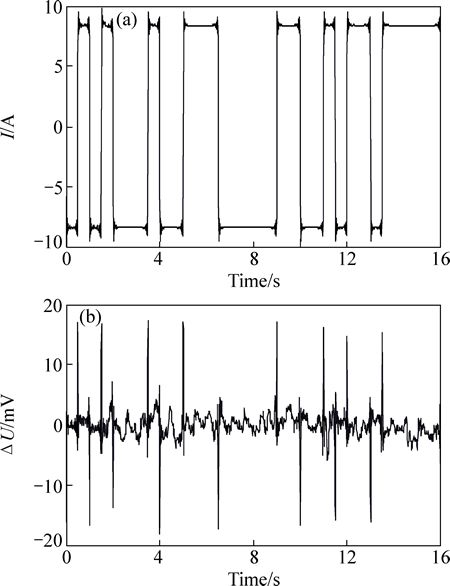
图6 测点No.44相关度最小的周期多频激电电流电压波形
Fig. 6 Current wave and potential difference wave of period at minimum coherency in survey point No.44
3 相关度分析方法应用效果分析
利用相关度分析方法对测线Line.1的所有测点数据进行处理。首先不采用相关度提取,对各测点利用所有周期的数据进行均值叠加计算。所得该测线复电阻率相位剖面和振幅剖面如图7和8所示。
由图7(a)和8(a)可以看出,在进行相关分析提取之前,800 m至1000 m (测点No.40至No.50)处由于电阻较低且测点距钻机较近,所得复电阻率相位和幅值计算结果都发生重大偏差,相位值在1000 mrad至3000 mrad左右,而电阻率幅值在50欧姆米以下,低频电阻率接近0,与实际情况不符。而且由图7(a)和图8(a)可以看出,相位误差超过1000 mrad,幅值误差超过100%,说明所得结果已严重失真。
然后采用相关度分析的方法对测线Line.1进行处理。对于测线上每一个测点,计算各周期电压、电流数据之间的相关度。当160个周期的相关度平均值大于0.5时,就以相关度平均值作为阈值,保留相关度均值以上的各周期数据。当160个周期的相关度平均值小于0.5时,就以0.5作为阈值,保留相关度在0.5以上的各周期数据。当160个周期的相关度最大值都小于0.5时,说明该测点数据质量特别差,这时仅保留相关度最大的N个周期,N值可以人为设定。本实验中各测点相关度最大值都大于0.5,所以仅需使用前两种阈值方法。采用相关度提取技术之后,各测点仅利用质量较好的周期的数据进行Robust周期叠加与后续计算。所得该测线复电阻率相位剖面和振幅剖面如图9和10所示。
由图9(a)和10(a)可以看出,采用相关度分析提取高品质数据进行Robust周期叠加及后续处理后,四个频点对应的复电阻率相位值在200 mrad至600 mrad之间,电阻率幅值在200 Ω左右,符合测区实际情况。处理之后,由图9(b)可以看出,相位误差降低到150 mrad以下,而且相对而言,高频成分对应的复电阻率误差更小,其中对应于0.66 Hz、0.91 Hz两个高频成分的相位误差降到40mrad以下。由图10(b)可以看出,复电阻率幅值误差都降到10%以内。整条剖面的曲线形态已比较合理。对于该测线中干扰严重的测点,虽然此次观测时间很长,原始数据有160个周期,但因为人为噪声的影响,导致大多数周期的数据失真,由于异常数据的比例高于50%,单纯使用Robust叠加方法也无法得到理想结果。而采用相干度分析处理之后,可以提取原始数据中质量较高的观测数据,剔除品质较差的观测数据。对于提取出的高品质数据,在每一个采样点的多周期观测值中,离群值的比例低于50%,这时进行Robust周期叠加及后续处理,可以得到更加准确的复电阻率计算结果。
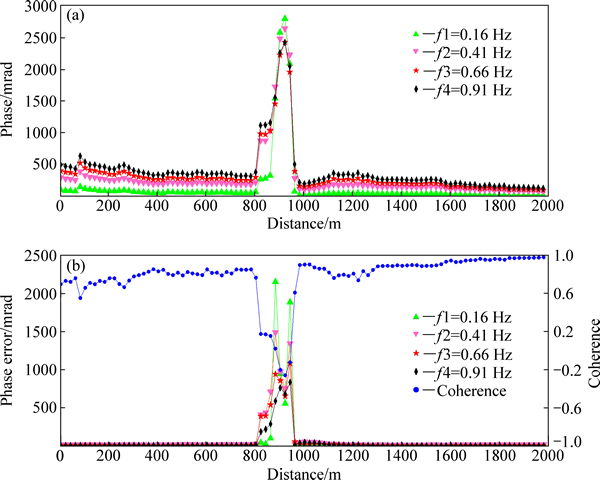
图7 测线Line.1所得4个频点对应的复电阻率相位剖面(采用相关度分析之前)
Fig. 7 Profile of complex resistivity phase for 4 frequencies in survey Line.1 (before coherence analysis processing)

图8 测线Line.1所得4个频点对应的复电阻率振幅剖面(采用相关度分析之前)
Fig. 8 Profile of complex resistivity amplitude for 4 frequencies in survey Line.1 (before coherence analysis processing)
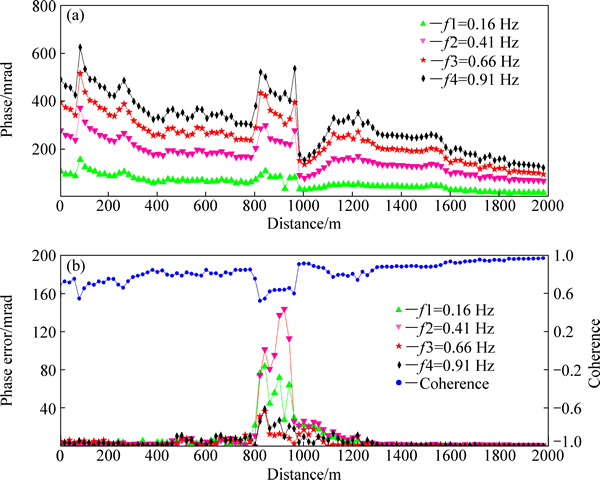
图9 测线Line.1所得4个频点对应的复电阻率相位剖面(采用相关度分析之后)
Fig. 9 Profile of complex resistivity phase for 4 frequencies in survey Line.1 (after coherence analysis processing)
由图9(a)和10(a)可以看出,处理之后800 m至1000 m(测点No.40至No.50)处仍有一定的低阻、高极化异常。结合测区地质等资料可知,该区域即为铅锌矿容矿断层所在位置。铅锌矿为低阻高极化,断层往南倾,倾斜方向与小号测点一致,类似于低阻高极化倾斜板状体。在图9(a)所示相位剖面中,在800 m至100 m 出现相移极大值异常,在极大值右侧有小于背景值的相移极小值异常出现。在图10(a)所示的电阻率幅值剖面中,在800 m至1000 m 出现电阻率极小值异常,在极小值右侧有略大于背景值的电阻率极大值异常出现。这与低阻高极化倾斜板状体的异常形态完全吻合,可见数据处理结果较好地反映了测区地质情况。

图10 测线Line.1所得4个频点对应的复电阻率振幅剖面(采用相关度分析之后)
Fig. 10 Profile of complex resistivity amplitude for 4 frequency in survey Line.1 (after coherence analysis processing)
4 结论
1) 将相关度分析引入多频激电数据预处理。对于噪声干扰严重的多周期观测数据,计算各周期电压、电流数据之间的相关度,相关度与实测数据的数据质量直接相关,根据相关系数分布范围,设置阈值进行滤波,可在强噪声干扰环境下提取出质量较高的观测数据,进而通过Robust周期叠加与后续处理,可以获得更为准确的复电阻率计算结果,由于该方法是基于叠前数据,所以不会带来激电信息的损失。
2) 结合甘肃白银地区某测线实测的多频激电数据证明了该方法的有效性。在进行相关分析提取之前,复电阻率相位和幅值计算结果都发生重大偏差,相位误差超过1000 mrad,幅值误差超过100%。采用相关度分析进行处理后,相位误差降低到150 mrad以下,幅值误差降到10%以内,对于高频成分,计算误差更小,相位误差降到40 mrad以内。
3) 虽然该段的计算误差相对于其他测点依然比较大,但处理后整条测线曲线形态已比较合理。测线所圈定的异常主要反映铅锌矿容矿断层,与先期地质资料相符。相关度分析处理方法原理简单,易于实现,有助于从强干扰背景下提取高品质多频激电信号,推动频谱激电法在矿产资源勘查中的应用。
致谢:感谢中南大学中央高校基本科研业务专项资金资助。感谢国防科技大学信息地球物理协同创新中心和湖南强军科技有限公司吴宏、姚红春、申瑞杰、石洪华、仇洁婷等在多频激电方法、仪器和数据处理研究方面给予的帮助。
REFERENCES
[1] 陈蜀雁, 刘永明. 双频激电法在阿勒泰山区快速找矿评价中的应用[J]. 中南大学学报(自然科学版), 2006, 37(3): 588-592.
CHEN Shu-yan, LIU Yong-ming. Application of dual-frequency induced polarization method in prospecting in Aletai region[J]. Journal of Central South South University (Science and Technology), 2006, 37(3): 588-592.
[2] HAN Shi-li, ZHANG Shu-gen, LIU Jian-xin, HU Hou-ji, ZHANG Wen-shan. Integrated interpretation of dual frequency induced polarization measurement based on wavelet analysis and metal factor methods[J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 1465-1471.
[3] LIU Hai-fei, LIU Jian-xin, GUO Rong-wen, TONG Xiao-zhong, GONG Lu, PENG Yan-hua. Development of multi-channel observation and inversion for IP electrical sounding method[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(3): 816-823.
[4] 杨振威, 郑 伟, 李晓斌, 王华峰. 频谱激电法的发展与展望[J]. 物探与化探, 2015, 39(1): 22-28.
YANG Zhen-wei, ZHENG Wei, LI Xiao-bin, WANG Hua-feng. The development and prospect of the spectral induced polarization method[J]. Geophysical and Geochemical Exploration, 2015, 39(1): 22-28.
[5] WAIT J R. CHAPTER 4-The variable-frequency method[C]// Overvoltage Researchs & geophysical Applications. Oxford: Pergamon Press, 1959: 29-49.
[6] ZONGE K L, WYNN J C. Recent advances and applications in complex resistivity measurements[J]. Geophysics, 2012, 40(5): 851-864.
[7] 郭 鹏, 肖 都, 石福升. 阵列相位激电法在弱极化异常区的试验效果[J]. 物探与化探, 2012, 36(5): 772-774.
GUO Peng, XIAO Du, SHI Fu-sheng. The experiment effects of array phase IP used in weak induced polarization area[J]. Geophysical and Geochemical Exploration, 2012, 5: 772-774.
[8] 何继善. 双频激电法[M]. 北京: 高等教育出版社, 2005: 11.
HE Ji-shan. Dual frequency induced polarization method[M]. Beijing: China Education Press, 2005: 11.
[9] 崔益安, 李西洋, 向恩明, 柳建新, 朱肖雄, 纪铜鑫, 佟铁钢. 基于粒子群优化的双频激电数据联合反演[J]. 中国有色金属学报, 2013, 23(9): 2498-2505.
CUI Yi-an, LI Xi-yang, XIANG En-ming, LIU Jian-xin, ZHU Xiao-xiong, JI Tong-xin, TONG Tie-gang. Joint inversion of dual frequency IP data using PSO[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(9): 2498-2505.
[10] 何继善.2n系列伪随机信号及应用[C]//臧绍先. 中国地球物理学会年刊. 西安: 西安地图出版社, 1998.
HE Ji-shan. 2n Pseudo-random signal and its application[C]// ZHANG Shao-xian. Annual of the Chinese Geophysics Society. Xi’an: Xi’an Map Press, 1998.
[11] 何继善, 柳建新. 伪随机多频相位法及其应用简介[J]. 中国有色金属学报, 2002, 12(2): 374-376.
HE Ji-shan, LIU Jian-xin. Pseudo-random multi-frequency phase method and its application[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(2): 374-376.
[12] 陈儒军, 何继善, 白宜诚, 汤井田. 多频激电相对相位谱研究[J]. 中南大学学报(自然科学版), 2004, 35(1): 106-111.
CHEN Ru-jun, HE Ji-shan, BAI Yi-cheng, TANG Jing-tian. The study of relative phase spectrum in multi-frequency induced polarization[J]. Journal of Central South University (Natural Science), 2004, 35(1): 106-111.
[13] XI X L, YANG H C, HE L F. Chromite mapping using induced polarization method based on spread spectrum technology[C]//SMITH B D. Symposium on the Application of Geophysics to Engineering and Environmental Problems, Denver: Environment and Engineering Geophysical Society, 2013: 1-7.
[14] 淳少恒, 陈儒军, 耿明会. 伪随机 m 序列及其在电法勘探中的应用进展[J]. 地球物理学进展, 2014(1): 439-446.
CHUN Shao-heng, CHEN Ru-jun, GENG Ming-hui. Review of the pseudo-random m sequence and its application in electrical prospecting of exploration geophysics[J]. Progress in Geophysics, 2014, 29(1): 439-446.
[15] 罗先中, 李达为, 彭芳苹, 罗林涛, 赵金水. 抗干扰编码电法仪的实现及应用[J]. 地球物理学进展, 2014, 29(2): 944-951.
LUO Xian-zhong, LI Da-wei, PENG Fang-ping, LUO Lin-tao, ZHAO Jin-shui. Implementation and applications of an coded electrical instrument with anti-interference ability[J]. Progress in Geophysics, 2014, 29(2): 944-951.
[16] XI X L, YANG H C, ZHAO X F, YAO H C, QIU J T, SHEN R J, WU H, CHEN R J. Large-scale distributed 2d/3d FDIP system based on Zigbee network and GPS[J]. HAGER J. Symposium on the Application of Geophysics to Engineering and Environmental Problems 2014. Boston: Society of Exploration Geophysicists and Environment and Engineering Geophysical Society, 2014: 130-139.
[17] 陈儒军, 何继善, 罗维炳, 颜 良, 朱德兵. 精密多频激电接收机设计与实现[C]//臧绍先. 中国地球物理学会第二十三届年会论文集. 青岛: 中国海洋大学出版社, 2007: 531.
CHEN Ru-jun, HE Ji-shan, LUO Wei-bing, YAN Liang, ZHU De-bing. Precision multi-frequency receiver design and realization for induced polarization[C]//ZANG Shao-xian. Annual of the Chinese Geophysical Society. Qingdao: Publishing House of Ocean University of China Press, 2007: 531.
[18] 赵璧如, 赵 健, 张洪魁, 钱 卫, 赵玉林, 钱复业. PS100型IP到端可控源高精度大地电测仪系统——CDMA技术首次在地电阻率测量中的应用[J]. 地球物理学进展, 2006, 21(2): 675-682.
ZHAO Bi-ru, ZHAO Jian, ZHANG Hong-kui, QIAN Wei, ZHAO Yu-lin, Qian Fu-ye. The PS100 high precision earth-eletrictity instrument system (IP to IP)with controllable source—Application of CDMA technology to the measurement of earth-resistivity for the first time[J]. Progress in Geophysics, 2006, 21(2): 675-682.
[19] 汤井田, 罗维斌. 基于相关辨识的逆重复m序列伪随机电磁法[J]. 地球物理学院, 2008, 51(4): 1236-1234.
TANG Jing-tian, LUO Wei-bin. Pseudo-randan electromagnetic exploration based on invert-repeated m-sequence correlation identification[J]. Chinese Journal of Geophys, 2008, 51(4): 1236-1234.
[20] 罗维斌, 李庆春, 汤井田. 编码电磁测探[J]. 地球物理学报, 2012, 55(1): 341-349.
LUO Wei-bin, LI Qing-chun, TANG Jing-tian. Coded source electromagnetic sounding method[J]. Chinese Journal of Geophysics, 2012, 55(1): 341-349.
[21] ZIOLKOWSKI A. Optimisation of MTEM parameters: U.S. Patent Application 12/235,927[P]. 2007-3-9.
[22] 罗延钟, 陆占国, 孙国良, 黄伟才, 高隆钦. 新一代电法勘查仪器——伪随机信号电法仪[J]. 地球物理学进展, 2015, 30(1): 411-415.
LUO Yan-zhong, LU Zhan-guo, SUN Guo-liang, HUANG Wei-cai, Gao long-qin. New generation of instruments for electrical and electromagnetic prospecting-Instruments using pseudo random signal[J]. Progress in Geophysics, 2015, 30(1): 411-415.
[23] 陈儒军. 伪随机多频电磁法观测系统研究[D]. 长沙: 中南大学, 2003.
CHEN Ru-jun. The study on pseudo-random multi-frequency electromagnetic prospecting system[D]. Changsha: Central South University, 2003.
[24] 刘春明. 伪随机激电多参数谱法研究[D]. 长沙: 中南大学, 2006.
LIU Chun-ming. The study about Multiparameter Spectrum Pseudo-random IP Method[D]. Changsha: Central South University, 2006.
[25] 李 荡, 李志华, 曾 信. 双频激电仪接收机[J]. 电子测量与仪器学报, 2011, 26(12): 1078-1085.
LI Dang, LI Zhi-hua, ZENG Xin. Receiver of dual-frequency IP instrument[J]. Journal of Electronic Measurement and Instrument, 2011, 12(26): 1078-1085.
[26] 瞿德福, 张云尔. 概述我国激电仪行业标准和国内外仪器水平[J]. 国外地质勘探技术, 1996(6): 12-23.
QU De-fu, ZHANG Yun-er. Outline of Induced Polarization Industry Standard and level of instruments at home and abroad[J]. Foreign Geoexploration Technology, 1996, 6: 12-23
[27] 崔燕丽. 伪随机多功能多频观测系统的数据处理研究[D]. 长沙: 中南大学, 2002.
CUI Yan-li. The study on data processing of pseudo-random multi-frequency electromagnetic prospecting system[D]. Changsha: Central South University, 2002.
[28] 姚红春. 三维谱激电分布式采集系统的设计与实现[D]. 中南大学, 2012.
YAO Hong-chun. The design and implementation of distributed 3D-SIP acquisition system[D]. Changsha: Central South University, 2012.
[29] LIU Wei-qiang, CHEN Ru-jun, WU Hong, QIU Jie-ting, YAO Hong-chun, REN Qiang, CHANG Fu-guo, ZENG Pei, LUO Wei-bin. High precision fdip exploration in productive mine with strong em interference[C]//CARR B J. Symposium on the Application of Geophysics to Engineering and Environmental Problems 2013. Austin: Society of Exploration Geophysicists and Environment and Engineering Geophysical Society, 2015: 65-73.
[30] 柳建新, 严家斌, 何继善, 等. 基于相关系数的海底大地电磁阻抗Robust估算方法[J]. 地球物理学报, 2003, 46(2): 251-255.
LIU Jian-xin, YAN Jia-bin, HE Ji-shan, Liu Chun-mng. Robust estimation method of sea magnetotelluric impedance based on correlative coefficient[J]. Chinese Journal of Geophysics, 2003, 46(2): 334-340.
[31] 薛军平, 龙 霞, 席振铢, 张道军, 李瑞雪, 王 鹤. 实测1~100 kHz大地电磁场分析[J]. 地球物理学进展, 2014, 29(6): 2566-2571.
XUE Jun-ping, LONG Xia, XI Zhen-zhu, ZHANG Dao-jun, lI Rui-xue, WANG He. Measured magnetotelluric field in 1~100 kHz frequency band. Progress in Geophysics, 2014, 29(6): 2566-2571.
[32] ROUBY D, XIAO H, SUPPE J. 3-D restoration of complexly folded and faulted surfaces using multiple unfolding mechanisms[J]. AAPG bulletin, 2000, 84(6): 805-829.
[33] STIGLER S M. Francis galton’s account of the invention of correlation[J]. Statistical Science, 1989(2): 73-79.
[34] HUBER P J. Robust statistics[M]. Springer Berlin Heidelberg, 1981.
[35] BUSELLI G, CAMERON M. Robust statistical methods for reducing sferics noise contaminating transient electromagnetic measurements[J]. Geophysics, 1996, 61(6): 1633-1646.
Coherence analysis for multi-frequency induced polarization signal processing in strong interference environment
LIU Wei-qiang1, 2, CHEN Ru-jun1, 2
(1. School of Geoscience and Info-physics Engineering, Central South University, Changsha 410083, China;
2. Key Laboratory of Nonferrous Metal Ore Forecast, Ministry of Education,
Central South University, Changsha 410083, China)
Abstract: Data processing in strong interference environment was investigated and coherence analysis was applied to do it. The coherence of potential difference and transmitting current for each period is relative to the data quality and the signal-to-noise ratio (SNR). SNR of data with coherence more than 0.5 can be high enough, which can be used for the subsequent data processing and resistivity calculation. In contrast, SNR of data with coherence less than 0.5 even close to 0 can be low and the IP signal is submerged by noise, which cannot be used for subsequent data processing. The effectiveness of our processing approach was demonstrated by showing examples of a data acquired in Gansu Province, Baiyin was demonstrated. The threshold is set and the observation data of high quality can be extracted to obtain more accurate calculation results of complex resistivity spectrum. For the survey point with strong interference, The error of complex resistivity phase is reduced from 1000 m/r to 150 m/r and error of complex resistivity phase at high frequency is reduced to 40 m/r. The error of complex resistivity amplitude is reduced from 100% to 10% approximately. This method is effective.
Key words: m-sequence multi-frequency induced polarization method; noise suppression; complex resistivity; coherence analysis; threshold
Foundation item: Project (2382014bks101) supported by the Fundamental Research Funds for Central South University, China
Received date: 2015-05-19; Accepted data: 2015-10-18
Corresponding author: CHEN Ru-jun; Tel: +86-13787080374; E-mail: chrujunl2458@gmail.com
(编辑 李艳红)
基金项目:中南大学中央高校基本科研业务专项资金资助(2382014bks101)
收稿日期:2015-05-19;修订日期:2015-10-18
通信作者:陈儒军,副教授,博士;电话:13787080374;E-mail:chrujun12358@gmail.com