求解任务分配问题的一种离散微粒群算法
王雅琳，王 宁，阳春华，桂卫华
(中南大学 信息科学与工程学院，湖南 长沙，410083)
摘 要：以交通运输领域中的装卸货任务分配问题为例对任务分配问题进行数学描述，提出一种用于求解该类问题的离散微粒群算法(DPSO)。在分析基本微粒群算法的收敛性能和任务分配问题解分布情况的基础上，采用惯性权值非线性下降策略更新微粒速度，以提高算法的收敛性，并且引入一个反正切函数对基本微粒群算法的位置公式进行进一步处理，以保证解的可行性。提出的DPSO用于求解某企业铁路货运站的装卸任务，在相同实验条件下，求解同一任务分配问题，提出的改进DPSO寻优率为76%，明显高于寻优率仅为40%和4%的其他2种DPSO算法；不同规模问题的求解试验中，综合比较寻优结果和计算时间，所提DPSO算法优于枚举法和遗传算法，且计算简便，可推广用于其他任务分配问题与组合优化问题。
关键词：微粒群算法；任务分配；惯性权值；离散问题
中图分类号：TP18 文献标识码：A 文章编号：1672-7207(2008)03-0571-06
A discrete particle swarm optimization algorithm for
task assignment problem
WANG Ya-lin, WANG Ning, YANG Chun-hua, GUI Wei-hua
(School of Information Science and Engineering, Central South University, Changsha 410083, China)
Abstract: Mathematical description of task assignment problem was given by describing the pickup and delivery task assignment problem in transportation, and a discrete particle swarm optimization algorithm (DPSO) for solving the above problem was proposed. Based on the analysis of convergence performance of standard PSO and distribution of solutions of the task assignment problem, the strategy of nonlinearly decreasing inertia weight was adopted in the velocity update formula to improve the convergence of the algorithm, and an arctangent function was introduced to further adjust the position formula to ensure the feasibility of solutions. The proposed DPSO was applied to the pickup and delivery task assignment in a railway freight station. Solving the same task assignment problem in the same experimental condition, the successful rate of the proposed DPSO is 76%, and is higher than those of the other two DPSO, which are only 40% and 4%. In the experiment of solving different scale problems, by comparing the optimization results and computing time, the proposed DPSO is superior to the enumeration method and genetic algorithm. The proposed algorithm is simple and feasible, and can be applied to solving other task assignment problems and combinational optimization problems.
Key words: particle swarm optimization algorithm; task assignment; inertia weight; discrete problem
任务分配问题是一类广泛存在于工农业生产、交通运输及服务行业的典型组合优化问题，目前在计算机并行计算领域也倍受关注。任务分配问题的优化目标是确定合理的子任务分配方案使所有任务的总完成时间最短，这是一个NP-complete问题
[1]，不存在按多项式时间复杂度找到全局最优解的算法
[2]。不过，近年来受自然隐喻启发而提出的一些智能计算方法(如遗传算法、模拟退火算法、蚁群算法和微粒群算法等)在问题规模较大时也能在可行时间范围内寻找到问题的满意解，为解决NP-complete问题提供了新的途径。
微粒群算法(particle swarm optimization，PSO)[3]最早由J. Kennedy和R. Eberhart[4-5]提出，其概念简单，实现容易，在连续优化问题中取得了大量的研究成 果[6-10]，而有关离散问题的应用和研究相对较少，目前，用于求解组合优化这类离散空间优化问题的思路主要有两类：一是限界取整法，即对传统PSO的结果按界限幅，并向上取整作为实际值。这类方法用于求解分布式计算机系统的任务分配问题[2]和带时间窗的车辆路径问题[11]，由于按界限幅，求解结果取边界值的几率较大，相对取中间值的几率减小，这种寻优的不公正使算法易陷入局部最优；二是交换序[12]及其类似方法[13-14]，这类方法重构PSO算法的运算法则实现离散问题的寻优，新的运算法则或更新方法，有时使PSO算法的计算机实现复杂化，失去了简便、容易实现的优点。
鉴于以上两类算法都存在不足，本文作者提出一种新的求解任务分配这类组合优化问题的离散微粒群算法。这种算法通过对基本PSO算法的更新使函数变化，来保证微粒的位置始终分布在实际值可能出现的范围之内，以避免边界限幅造成的寻优不公正现象。此外，考虑到速度更新中惯性权值对算法收敛性的影响，改进惯性权值下降策略[15]，以进一步提高算法的收敛速度。以交通运输领域的装卸货任务分配问题为例，探讨算法的实现，并通过仿真验证所提算法的有效性。
1 任务分配问题的数学描述
机床加工、货物装卸、并行计算等都存在任务分配问题，下面以交通运输领域中的装卸货问题为例进行数学描述。假设某货运站有m列待装卸货车和n支装卸队(m＞n)，已知每列车货物装载量为wi (单位为t，i表示第i列车)，每个装卸队的装卸能力为Qk (单位为t/h，k表示第k个装卸队)，任务分配的目标是把这m列车合理地分配给n支装卸队，以使总的货物装卸时间最短。由于n支装卸队是并行作业的，相当于使装卸时间最长的装卸队其作业时间最短。
定义决策变量X=(x1, x2, …, xm) 表示m列车分给n支装卸队装卸的分配情况。若第i列车分配给第k个装卸队装卸，则xi=k，即xi的取值为1到n之间的整数；令ek表示第k支装卸队的装卸作业时间(k=1, 2, …, n)，其中：
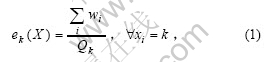
则任务分配问题的数学模型可表示为
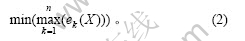
式(2)描述的任务分配问题具有普遍性。若令wi和Qk分别表示第i种待加工工件的个数和第k个机床的单位加工时间，则式(2)所描述的就是一个机床加工的任务分配问题。当然，许多情况下加工工件的机床是相同的(即单位加工时间相同)，这时ek(X)的表达式可以简化为不考虑式(1)中的Qk。对于一个计算机并行计算的任务分配问题，式(2)中的ek(X)表示两部分之和：一部分为类似式(1)的处理器计算执行时间；另一部分则为分配给某处理器任务与没分配给该处理器的任务之间通讯的交互时间[2]。由于式(2)的表达式为任务分配问题的一般描述，根据具体问题的不同，式(2)中的ek(X)可以简单也可以复杂，所以，本文以装卸货任务分配为例研究的优化算法可推广到其他任务分配中。
2 离散微粒群算法
2.1 微粒群算法
与其他进化算法类似，微粒群算法(PSO)也是通过个体间的协作与竞争来实现复杂空间中最优解的搜索。PSO算法的数学描述为：在一个D维的搜索空间中，有m个微粒组成一个种群，第i个微粒的位置为Xi=(xi1, xi2, …, xiD)T，速度为Vi=(vi1, vi2, …, viD)T，第i个微粒迄今为止搜索到的最好位置为Pi=(pi1, pi2, …, piD)T，整个种群搜索到的最好位置为Pg=(pg1, pg2, …, pgD)T，则对于每一次迭代，微粒i的第d维 (1≤d≤D)根据式(3)和式(4)更新自己的速度和位置：
式中：i=1, 2, …, m；d=1, 2, …, D；k为迭代数，c1和c2为学习因子(或称作加速系数)；w为惯性权重。
r1和r2是2个在[0, 1]范围内变化的随机数。此外，为使微粒速度不致过大，可设定速度上限vmax，即对于式(3)中vid，当vid＞vmax时，取vid=vmax；当vid＜-vmax时，vid=-vmax。
2.2 惯性权值改进策略
Y. Shi等[15]分析了惯性权值w对优化性能的影响，在此基础上，提出了线性递减的w自适应调整策略。然而，PSO搜索过程是一个非线性的复杂过程，w线性递减策略使得w保持较大值和较小值的时间都很短，并不能正确地反映真实的搜索过程。考虑w对算法收敛过程的影响，希望w在整个搜索过程的前期能较长时间保持较大值，以保证算法具有较高的全局搜索能力和较快的搜索速度，而在后期又能较长时间地保持较小值，以使其具有较高的搜索精度。因此，提出了w按式(5)进行非线性调整的改进策略。
如图1中曲线1所示，w的下降曲线为一类“S”型曲线，该曲线由2个抛物线组合而成：上抛物线开口向下，顶点在 (0, wmax)，下抛物线开口向上，顶点坐标为 (Tmax, wmin)，两抛物线的连接点为(0.5Tmax, 0.5(wmax+wmin))。
1—w非线性下降曲线；2—w线性下降曲线
图1 w下降曲线
Fig.1 Decreasing curves of w
2.3 求解任务分配问题的微粒群算法
用PSO算法求解任务分配问题时，令PSO算法中每个微粒代表决策变量的1个可能取值，该微粒为m维，其位置的第i维代表第i列车该由哪个装卸队完成，其取值为1~n中的任意1个整数。由基本微粒群算法的更新式(4)不难看出，其位置并非离散的，而是可能取到-∞~+∞中的任何数。为此，提出一种离散微粒群算法(discrete particle swarm optimization, DPSO)，对微粒的位置进行处理，使其取值范围由-∞~+∞的连续数转化为1~n之间的整数，以适应任务分配问题的求解。
已知反正切函数arctan的自变量取值为 (-∞, +∞)，因变量取值为(-π/2, π/2)。因此，在DPSO中，首先对基本微粒群算法所求解到的位置进行函数变化：
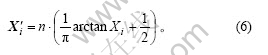
从而将微粒位置的连续取值范围由(-∞, +∞)压缩到(0，n)；然后，对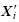
向上取整，最终得到1~n之间的整数。
按以上思路，离散微粒群算法(DPSO)求解任务分配问题的步骤如下。
步骤1 初始化微粒群。包括微粒群的规模，每个微粒的初始位置与初始速度。
步骤2 按式(2)评价每个微粒的初始适应值。将初始评价值作为个体历史最优解Pbest，并求得全局最优解Gbest。
步骤3 根据式(5)计算惯性权值w，并按式(3)更新微粒的速度。
步骤4 根据式(4)更新微粒的位置，然后，根据式(6)对位置作进一步调整，最后将调整后的结果向上取整，得到任务分配问题的可行解。
步骤5 根据式(2)重新评价各微粒的适应值。若微粒的当前适应值优于Pbest，则令当前适应值为Pbest，并保存当前位置为其个体历史最优位置。
步骤6 比较群体中所有微粒的Pbest和Gbest，若某微粒的Pbest优于Gbest，则令该微粒的Pbest为Gbest，并保存该微粒的当前位置为全局历史最优位置。
步骤7 判断是否满足终止条件。若达到最大迭代次数，则停止搜索，输出寻优结果；否则，转到步骤3继续搜索。
3 实例验证
为验证所提离散微粒群算法求解任务分配问题的可行性、有效性和先进性，在Pentium Ⅳ/1.7G/256M计算机上，基于C语言进行了一系列仿真实验和算法比较实验。
首先，以某企业铁路货运站一个L10-3的装卸任务为例进行仿真实验。已知该装卸任务有10列车，可分别由3支装卸队完成装卸任务。列车和装卸队的具体情况如表1所示。
表1 10列车装卸货的已知条件
Table 1 Known conditions of pickup and delivery of 10 trains
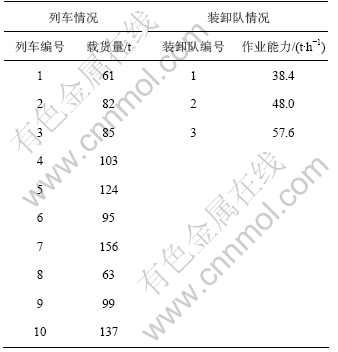
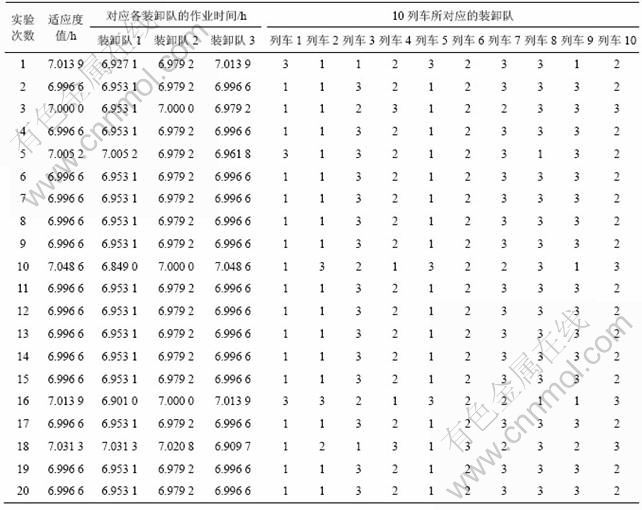
L10-3任务分配问题的求解规模不大，用枚举法求解得最佳任务分配方案为[1, 1, 3, 2, 1, 2, 3, 3, 3, 2]，且装卸队1，2和3的作业时间分别为6.953 1，6.979 2和6.996 6 h。若用本文提出的离散微粒群算法进行求解，参数设置为：群体数目为30，c1=c2=2，wmax=0.9，wmin=0.1，vmax=2，最大迭代次数为2 000次。微粒群算法20次实验的寻优结果如表2所示。
从表2可以看出，20次的求解结果中，有14次达到最优值，并且其他6次的结果也相对比较理想，偏差不大。可见，采用所提算法求解任务分配问题是可行的和有效的。
表2 粒子群算法寻优结果
Table 2 Optimal search results of PSO
其次，为证实所提微粒群算法改进策略的有效性和先进性，仍以表1中的L10-3任务分配为例进行仿真实验。表3所示为各种PSO算法在相同实验条件下(即PSO参数设置均为表2实验时所设参数)分别50次仿真实验的结果。其中，DPSO1算法采用w线性下降策略和本文提出的函数变化后再取整的离散策 略，DPSO2算法采用w非线性下降策略和本文提出的函数变化后再取整的离散策略，DPSO3算法采用w非线性下降策略和文献[2，11]中提出的限界取整的离散策略。
表3 各种PSO算法求解结果比较
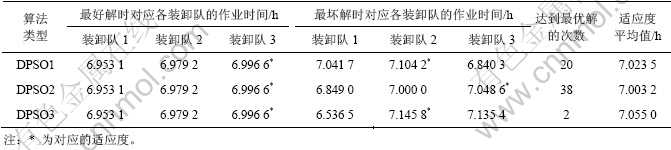
从表3可以看出，求解任务分配问题时，PSO算法采用函数变化后取整结果优于限界取整结果，惯性权值非线性下降优于线性下降。采用限界取整法求解任务分配时容易陷入局部最优解，而DPSO2(即本文所提算法)跳出局部极值的能力明显增强。
最后，在求解大规模任务分配问题时进行PSO算法先进性的验证实验。对于不同规模的任务分配问题，表4给出了枚举法、本文所提DPSO以及遗传算法(GA)3种算法的求解结果，其中DPSO和GA是50次实验求解结果的平均值。DPSO和GA参数设置如下：种群规模均为实际问题规模的3倍，即L10-3，L10-4为30，L20-4，L20-5为60，L30-5为90，迭代次数均为2 000次，DPSO中c1=c2=2，wmax=0.9，wmin=0.1，vmax=2。GA中采用轮盘赌选择算子，单点交叉，均匀变异，交叉概率设为0.8，变异概率设为0.01。
由表4可以看出，当问题规模扩大时，无论是车列增加还是装卸队数增加，若用枚举法求解，则需一一列举的次数以指数增长的方式增加，计算相当耗时，甚至使计算机陷入瘫痪状态。而采用DPSO和GA等智能算法仍能在可行时间内给出满意解，且DPSO相对于GA具有更为理想的求解性能。
表4 不同规模问题的各种算法求解结果比较
Table 4 Results comparison of algorithms solving different scale problems
4 结 论
a. 以交通运输领域中的装卸货任务分配问题为例，给出了任务分配问题的数学描述。提出了一种求解任务分配问题的离散微粒群算法。通过对基本微粒群算法所求得的微粒位置进行函数变化再取整，从而保证其取值始终为任务分配问题的可行解；考虑到惯性权值对优化性能的影响，提出了惯性权值非线性下降策略，以提高算法的收敛性。
b. 在相同实验条件下，进行了一系列实验。用各种PSO算法对L10-3任务分配问题进行求解，所提改进DPSO的寻优率为76%，明显优于其他2种DPSO算法(寻优率分别为40%和4%)；分别用枚举法、遗传算法和所提DPSO算法对不同规模的任务分配问题进行求解，结果证实在相同规模下DPSO优于遗传算法，枚举法适用于求解较小规模问题，而规模较大时难以求解。
c. 所提算法可推广应用于其他的各种组合优化问题中，具有一定的广泛性和适应性。
参考文献：
[1] Garey M R, Johnson D S. Computers and intractability: A guide to the theory of NP-completeness[M]. New York: Freeman, 1979.
[2] Salman A, Ahmad I, Al-Madani S. Particle swarm optimization for task assignment problem[J]. Microprocessors and Microsystems, 2002, 26: 363-371.
[3] 谢晓锋, 张文俊, 杨之廉. 微粒群算法综述[J]. 控制与决策, 2003, 18(2): 129-134.
XIE Xiao-feng, ZHANG Wen-jun, YANG Zhi-lian. Overview of particle swarm optimization[J]. Control and Decision, 2003, 18(2): 129-134.
[4] Kennedy J, Eberhart R C. Particle swarm optimization[C]// Proceedings of IEEE International Conference on Neural Networks. Piscataway: IEEE Service Center, 1995: 1942-1948.
[5] Eberhart R C, Kennedy J. A new optimizer using particle swarm theory[C]//Proceedings of 6th International Symposium on Micromachine and Human Science. Piscataway: IEEE Service Center, 1995: 39-43.
[6] Eberhart R C, Shi Y. Particle swarm optimization: Developments, applications and resources[C]//Proceedings of Congress on Evolutionary Computation. Piscataway: IEEE Service Center, 2001: 81-86.
[7] Ourique C O, Biscaia E C Jr, Pinto J C. The use of particle swarm optimization for dynamical analysis in chemical processes[J]. Computers and Chemical Engineering, 2002, 26(12): 1783-1793.
[8] ZHOU Jia-lin, DUAN Zheng-cheng, LI Yong, et al. PSO-based neural network optimization and its utilization in a boring machine[J]. Journal of Materials Processing Technology, 2006, 178(1/3): 19-23.
[9] Fan S K S, Zahara E. A hybrid simplex search and particle swarm optimization for unconstrained optimization[J]. European Journal of Operational Research, 2007, 181(2): 527-548.
[10] 李 婷, 赖旭芝, 吴 敏. 基于双种群粒子群优化新算法的最优潮流求解[J]. 中南大学学报: 自然科学版, 2007, 38(1): 133-137.
LI Ting, LAI Xu-zhi, WU min. A novel two-swarm based particle swarm optimization algorithm for optimal power flow problem[J]. Journal of Central South University: Science and Technology, 2007, 38(1): 133-137.
[11] 李 宁, 邹 彤, 孙德宝. 带时间窗车辆路径问题的粒子群算法[J]. 系统工程理论与实践, 2004, 24(4): 130-135.
LI Ning, ZOU Tong, SUN De-bao. Particle swarm optimization for vehicle routing problem with time windows[J]. System Engineering Theory and Practice, 2004, 24(4): 130-135.
[12] 黄 岚, 王康平, 周春光, 等. 粒子群优化算法求解旅行商问题[J]. 吉林大学学报: 理学版, 2003, 41(4): 477-480.
HUANG Lan, WANG Kang-ping, ZHOU Chun-guang, et al. Particle swarm optimization for traveling salesman problems[J]. Journal of Jilin University: Science Edition, 2003, 41(4): 477-480.
[13] 肖健梅, 黄有方, 李军军, 等. 基于离散微粒群优化的物流配送车辆路径问题[J]. 系统工程, 2005, 23(4): 97-100.
XIAO Jian-mei, HUANG You-fang, LI Jun-jun, et al. Vehicle routing problem based on discrete particle swarm optimization[J]. Systems Engineering, 2005, 23(4): 97-100.
[14] 钟一文, 杨建刚. 独立任务分配问题的离散粒子群优化算法[J]. 模式识别与人工智能, 2006, 19(3): 399-406.
ZHONG Yi-wen, YANG Jian-gang. Discrete particle swarm optimization algorithm for independent task assignment problem[J]. Pattern Recognition and Artificial Intelligence, 2006, 19(3): 399-406.
[15] Shi Y, Eberhart R C. A modified particle swarm optimizer[C]// Proceedings of the 1998 Conference of Evolutionary Computation. Piscataway: IEEE Press, 1998: 69-73.
收稿日期：2007-09-22；修回日期：2007-12-13
基金项目：国家自然科学基金资助项目(60574030)；湖南省自然科学基金资助项目(06FD026)
通信作者：王雅琳(1973-)，女，广东惠州人，副教授，博士后，从事复杂工业过程建模\优化与控制以及人工智能、智能计算等研究；电话： 0731-8876864；E-mail: ylwang@mail.csu.edu.cn
