J. Cent. South Univ. (2016) 23: 333-343

DOI: 10.1007/s11771-016-3078-0

Parametric analysis of thermal effect on hydrostatic slipper bearing capacity of axial piston pump

TANG He-sheng(汤何胜), YIN Yao-bao(訚耀保), ZHANG Yang(张阳), LI Jing(李晶)

School of Mechanical Engineering, Tongji university, Shanghai 201804, China

 Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: Hydrostatic slipper was often used in friction bearing design, allowing improvement of the latter’s dynamic behavior. The influence of thermal effect on hydrostatic slipper bearing capacity of axial piston pump was investigated. A set of lumped parameter mathematical models were developed based on energy conservation law of slipper/ swash plate pair. The results show that thermal equilibrium clearance due to solid thermal deformation periodically changes with shaft rotational angle. The slipper bearing capacity increases dramatically with decreasing thermal equilibrium clearance. In order to improve the slipper bearing capacity, length-to-diameter ratio of fixed damper varies from 3.5 to 8.75 and radius ratio of slipper varies from 1.5 to 2.0. In addition, the higher slipper thermal conductivity is useful to improve slipper bearing capability, but the thermal equilibrium clearance is not compromised.

Key words: axial piston pump; slipper friction pairs; oil film; load carrying capacity

1 Introduction

Axial piston pump is widely used in hydraulic systems because of its advantages, such as high power density, high limit pressure and long service life. There are several challenging issues associated with the pump, such as conflicts between lubrication and wear, and between sealing and leakage. For severe operating conditions, the temperature rise in lubricating region of friction pairs may not be ignored. Particularly, slipper friction pairs are the key friction parts of a hydraulic axial piston pump and directly affects the performance and service life of the pump. There have been many publications in this general subject area over the past 30 years, many concerned with improving the slipper performance. Most of the work has been focused on analyzing the forces and torques over the slipper, experimentally, analytically and via numerical simulation [1-2]. The effects of slipper spin, tangential velocity, tilt, slipper non flatness, inlet orifice, and conditions for material to material contact, amongst others, have been investigated [3-6]. MANRING et al [7] studied the effects of pressure induced deformations on the characteristics of hydrostatic thrust bearing. The most advanced analytical study on non-tilt slipper without a groove was presented by JOHNSON and MANRING [8], where Reynolds equation of lubrication was integrated considering the effect of tangential velocity. WIECZOREK and IVANTYSYNOVA [9] conducted nonlinear computer simulation on the sliding surfaces in an axial piston machine using non-isothermal laminar lubrication theory. KAZAMA [10] investigated the influence of oil physical properties on hybrid thrust bearing thermohydrodynamic performance and considered various operation conditions. For the case of non-tilted slipper with a groove, an introductory work was presented by KUMAR et al [11], where the flow vorticity inside the groove was numerically determined for different groove dimensions. In addition, BERGADA et al [12] studied an analytical approach towards the understanding of the hydrostatic leakage and lift characteristic of a flat slipper used for piston slipper units within an axial piston pump. WANG and YAMAGUCHI [13-14] clarified experimentally and theoretically the effects of nozzle and thermoplastic materials on the characteristics of hydrostatic bearing/ seal parts in water hydraulic axial pumps and motors. CANBULUT et al [15] designed a neural network predictor of the analysis of leakage rate in the design of partially hydrostatic slipper bearing.

Most of the abovementioned models calculated dynamic performance of slipper friction pairs under isothermal condition, in which the interactions between temperature and other variables were ignored [16-20]. Therefore, it is desirable to develop a numerical model that analyzes thermodynamic behavior of slipper friction pairs. The absence of such a model is mainly due to the difficulties in handling numerical convergence problem and excessive computation efforts. The recent new development of the thermodynamic modeling in the axial piston pump is presented by LI and JIAO [21]. ZOU et al [22] used Matlab/Simulink to simulate the mathematical model of thermodynamic processes in a twin-rotor piston engine. MA and ZHU [23] experimentally studied the temperature response and distribution in a sector tilted pad thrust bearing during the transient periods, such as the load on the bearing changed abruptly. GLAVATSKIH et al [24] investigated experimentally and theoretically the effect of oil thermal properties on the performance of a tilting-pad thrust bearing. In the present work, a numerical thermal hydraulic model is developed that takes solids temperature and heat transfer process in consideration. The effects of structure parameters and material properties on hydrostatic slipper bearing capacity are analyzed.

2 Theoretical description

2.1 Operating principle of axial piston pump

The schematic diagram of a typical axial piston pump is shown in Fig.1. The typical piston pump mainly consists of the following hydraulic components: a cylinder block, a shaft, a valve plate, a swash plate, nine pistons and nine slippers. The valve plate has two windows for oil suction and oil discharge, respectively. When the cylinder block and shaft rotate clockwise, the piston moves within the cylinder towards the valve plate and discharges the fluid in the piston chamber to the discharge port. Then, the piston begins to move toward the swash plate and the fluid rushes into the piston chamber through the suction port. The discharge and suction processes define one completed pumping cycle for one piston. Of course, other than the main flow through the piston chambers, certain leakage flow takes place in the pump. As shown in Fig. 1, the leakage flow is through the clearance between the slipper and swash plate. The leakage flow depends on the pressure differential between single piston chamber and the respective flow path resistance.

Fig. 1 Schematic diagram of axial piston pump

2.2 Scheme of hydrostatic slipper

The schematic diagram of hydrostatic slipper is shown in Fig. 2. The hydrostatic slipper consists of a fixed damper and a changeable damper. The annular orifice typed fixed damper is employed to inject fluid into the slipper pocket. The changeable damper between slipper and swash plate varies with the pressure load. When the pressurized oil flows through the fixed damper, its pressure p decreased to p_s. The pressure inside slipper pocket can pass through the sealing region of slipper and generate a pressure field, which would create a hydrostatic force to support the load and form a lubrication film. When the load increases and thus destroys the balance between the load and the hydrostatic force, the clearance between slipper and swash plate would be diminished. Sequentially, the changeable damper of clearance would rise up, and the flow through the clearance would be reduced. Then, the reduced flow denotes that the leakage rate through the changeable damper is reduced, which could lead to the pressure differential being decreased. Consequently, the pressure p_s could rise up to enhance the hydrostatic force for balancing the increased pressure load.

Fig. 2 Schematic diagram of hydrostatic slipper

3 Mathematical modeling of hydrostatic slipper

3.1 Governing equations

The mechanical energy dissipation due to viscous friction converts into heat flux when the fluid flows through the clearance between slipper and swash plate. The heat flux contributes to increasing the solid temperature and thermal expansion. The overall result is that solid thermal expansion modifies the clearance between slipper and swash plate. Considering fully developed laminar flow in the leakage path, corresponding pressure-discharge equations are obtained. With reference to Fig. 2, the leakage rate generated by hydrostatic slipper can be expressed as

                           (1)

where q₀ is leakage flow; d is damping diameter of slipper; l is damping length of slipper; μ is oil viscosity; p is fluid pressure in piston chamber; p_s is pocket pressure.

Assuming that the leakage rate through the clearance between slipper and swash plate is laminar and its fluid pressure profile is a natural logarithmic type curve at the sealing region of slipper, it can also be written as

                         (2)

where R is outside radius of slipper; r₀ is insider radius of slipper; δ is thermal equilibrium clearance between slipper and swash plate.

According to the principle of fluid continuity, fluid pressure in slipper pocket can be derived from Eqs. (1) and (2) as

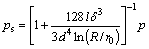                     (3)

The fluid pressure in slipper pocket is related closely with the fluid pressure in piston chamber. As the piston periodically pass over the discharge and suction ports on the valve plate, each piston chamber experiences its oven pressure history. Due to the fluid pressure variation in piston chamber, the magnitude of the normal load which acts on the slipper in axial piston pump varies during one shaft rotation. Thus, the time-varying fluid pressure based on the compressible fluid continuity equation can be defined as

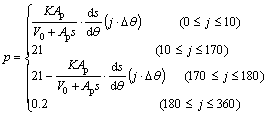   (4)

where V₀ is initial voloume of piston chamber; A_p is area of piston chamber; K  is volme modulus; s is piston displacement; j is number; θ is shaft rotational angle; △θ is rotational angle increment.

Thermal equilibrium clearance and slipper bearing capacity are shown in Fig. 3. The energy dissipated between slipper and swash plate heats up fluid in the clearance. This leads to a change of local fluid viscosity, which speeds up fluid velocity in the clearance. Finally, the slipper bearing capability decreases, and this phenomenon causes sever wear problems or even metal to metal contact. To avoid any thermal problem of axial piston pump, the determination of thermal equilibrium clearance between slipper and swash plate is necessary. Thus, fluid energy conservation relationship in the clearance between slipper and swash plate is written as

                (5)

where  is slipper tangential velocity; n is shaft speed; R_f is distribution radius of slipper; 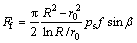 is slipper friction force; f is friction coefficient; β is swash plate angle; T_f is film temperature; T₀ is initial film temperature; ΔT is film temperature difference; c_p is fluid specific heat capacity; ρ is the density.

Oil viscosity is closely related to oil temperature at the clearance between slipper and swash plate in axial piston pump. The selection of hydraulic oil depends on specific operating condition of axial piston pump. We can find that the Reynolds viscosity-temperature equation can correctly fit the viscosity-temperature relationship when axial piston pump operates at high rotational speed and pressure condition. The oil viscosity as a function of oil temperature can be written as [25]

      (6)

where λ_T is the viscosity-temperature coefficient, λ_T=0.047 at oil temperature of 40 °C; μ₀ is initial oil viscosity.

Fig. 3 Thermal equilibrium clearance and slipper bearing capacity

As a matter of fact, the range of oil temperature rise in the clearance between slipper and swash plate is 10 °C to 30 °C. Under this fact, the oil viscosity can also be expressed as

                 (7)

Substituting Eqs. (7) into (5) yields

         (8)

In practice, the surface temperature of solids, such as slipper and swash plate parts, is calculated based on the determination of energy dissipation and heat transfer at the clearance. Furthermore, the heat flux generated by viscous friction is accumulated at the clearance. Fluid energy equation in steady state is considered, simplifying the thermal behavior of fluid film. When pump runs under steady-state condition, the heat fluxes to slipper and swash plate parts are determined based on the principle of heat fluxes distribution that is related to material properties. The fluid film fluxes to the solid parts are a function of oil temperature differential at the slipper and swash plate walls. Thus, the heat flux to slipper is written as

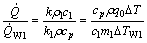                     (9)

and the heat flux to swash plate is written as

                   (10)

where  is heat flux of fluid film;  is heat flux of slipper;  is heat flux of swash plate; c₁ is slipper specific heat capacity; c₂ is swash plate specific heat capacity; m₁ is slipper mass; m₂ is swash plate mass; ΔT_w1 is slipper temperature differential; ΔT_w2 is swash plate temperature differential; ρ is oil density; ρ₁ is slipper density; ρ₂ is swash plate density; k is fluid thermal conductivity; k₁ is slipper thermal conductivity; k₂ is swash plate thermal conductivity.

High energy dissipation emphasizes the effect of solid thermal deformation on the slipper/swash plate- lubricating interface behavior. The impact of solid thermal deformation on the clearance between slipper and swash plate can be noticed. Therefore, the thermal equilibrium clearance between slipper and swash plate is expressed as

               (11)

where h₀ is initial film thickness; H₁ is slipper height; H₂ is swash plate height; α₁ is linear expansion coefficient of slipper; α₂ is linear expansion coefficient of swash plate.

Substituting Eqs. (7), (8), (9), (10) into (11) yields

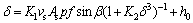             (12)

where

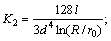
Equation (12) about δ is derivative as

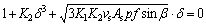           (13)

The minimum thermal equilibrium clearance (δ_min) between slipper and swash plate in thermodynamic equilibrium state can be obtained by Eq. (13). It can be deduced from Eq. (13) that if δ＞δ_min, slipper can operate normally in thermodynamic equilibrium state although the film gap is reduced due to slipper thermal expansion. However, when δ＜δ_min, slipper is unable to operate normally in thermodynamic equilibrium state.

As is seen in Fig. 3, hydrostatic slipper is held in equilibrium state by slipper pocket pressure. Under this condition, the slipper bearing capacity can be expressed as

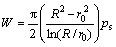                         (14)

where W is slipper bearing capacity.

From Eq. (14), the slipper bearing capacity is proportional to the pocket pressure. It can be deduced from Eq. (3) that high length-to-diameter ratio of fixed damper would bring about the pocket pressure, implying high slipper bearing capacity. In addition, it is not difficult to calculate the pocket pressure because the pressure is only dependent on the thermal equilibrium clearance after the slipper geometry is determined.

3.2 Solution procedure

The schematic flowchart for thermal equilibrium clearance and slipper bearing capacity computations can be described in Fig. 4. A shaft revolution in axial piston pump is simulated, solving slipper bearing capacity in time at discrete intervals, corresponding to a progressively increasing shaft rotational angle and different load conditions. The aforementioned governing equations are simultaneously solved based on numerical method. Slipper pocket pressure and slipper motion are obtained by finite difference method for calculating thermal equilibrium clearance and bearing capacity. Once the pocket pressure is obtained, the leakage rate could be solved since the slipper structure parameters and initial film thickness are given. To obtain oil film temperature, the fluid energy dissipation and oil viscosity due to the dynamic film temperature variation are updated at each shaft rotational angle. In addition, the heat fluxes between fluid film and solid are calculated at each simulation step. At the end of the shaft revolution, the heat fluxes are used to determine the solids temperature differential, such as swash plate and slipper parts. At the last step, the thermal equilibrium clearance due to solid thermal deformation is predicted since the solid temperature differential is given. The operation procedure continues to calculate thermal equilibrium clearance over one shaft revolution until oil film temperature reaches a stable value.

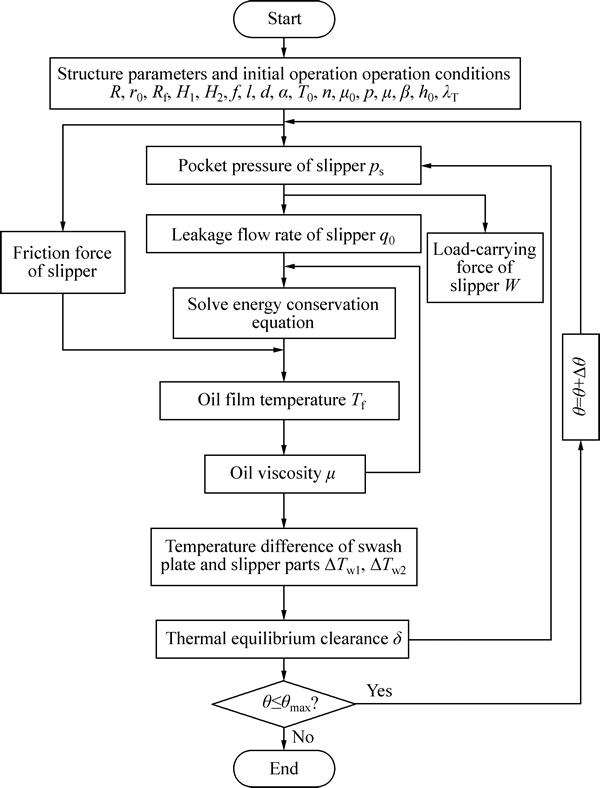
Fig. 4 Schematic flow chart for thermal equilibrium clearance and slipper bearing capacity computations

4 Experiment design and analysis

In order to evaluate the thermal clearance and slipper bearing capacity, the principle diagram of test bench system is depicted as shown in Fig. 5. The test bench system mainly contains tested pump and the loading device. A test pump is designed to take micrometric displacement measurement over the active lubrication interface of the slipper friction pairs. The slipper can be equipped with the eddy current displacement transducer (EddyNCDT3100-EU05) for the determination of the film thickness. The displacement signals are acquired by data acquisition unit and then are sent to industrial computer. The tested pump is driven by a 90 kw electrical motor (YVF280M-4) and a shaft couplings. The angle of swash plate is 17° and the diameter of piston is 20 mm while its distribution radius in reference to the rotating axis of swash plate is 46.8 mm. In this loading device, the medium used in the apparatus is oil, which is purified through a 10 μm filter. The pressurized oil is supplied by a hydraulic pump. The system pressure could be regulated from 1 MPa to 28 MPa through a throttle valve, and the flow rate could be adjusted from 63 L/min to 189 L/min by means of an axial piston pump driven by a frequency inverter (from 700 r/min to 2100 r/min). Relief valves A and B act as a safety support system. The testing temperature of fluid medium is controlled within the range of 40-55 °C.

Figure 6 illustrates locations of displacement sensors. There are eight eddy current displacement sensors. Each pair of sensors is circumferentially positioned at 45° intervals. For measuring oil film thickness, the sensors are mounted on the swash plate along the motion trajectory of slipper. The pitch diameter of the sensors’ location on the swash plate is 46.8 mm. When slipper runs along the swash plate surface through the suction pressure and discharge pressure regions of valve plate, the clearance between slipper and swash plate is obtained from the differences in output signals of the paired displacement sensors. All displacement sensors are placed in swash plate, where they are exposed to oil. The film thickness is measured by means of displacement sensor with the threshold of 0.5 mm and a measuring range from 0 to 0.5 mm. The film thickness is measured with an accuracy of 0.01 μm.

Fig. 5 Principle diagram of test bench system

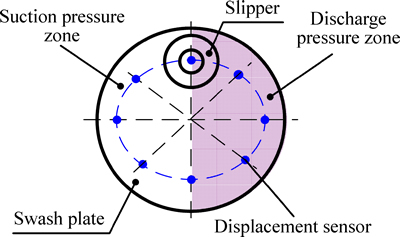
Fig. 6 Locations of displacement sensors

To obtain the actual clearance between slipper and swash plate, first the offset distance should be determined. It is a reference dimension to calculate the axial clearance. Figure 7 shows the proposed experimental structure system and its main components. The configuration of clearance-sensing system consists of one eddy current sensor, a signal-conditioning electronics, and a data acquisition system based on virtual instrument technology. The data acquisition board type is NI USB-6218 with high sampling rate. Its main parameters are as follows: the sampling frequency 100 kS/s, input resolution 16 bits, and accuracy 2100 μm when DC 0-10 V output voltage is selected. In this application, the sensor is mounted on the swash plate with offset installation. In order to determine the offset distance, the experiment can be done with the help of a test slipper, which is made to move in a rotating motion on the internal surface of swash plate. When the test slipper is covered over the sensor, the output voltage signal reflects the offset distance. After determining the offset, the sensor should be kept in the same position for the next experiment. The eddy current sensor could respond to the variation of axial clearance and the measured instantaneous clearance.

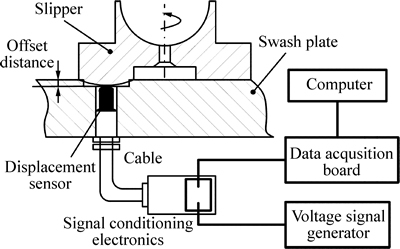
Fig. 7 Schematic of experimental device for measuring clearance

5 Results and discussion

The thermal equilibrium clearance and slipper bearing capacity are calculated respectively in the Matlab environment. In high pressure and speeds condition, hydrostatic and hydrodynamic behavior of slipper in axial piston pump is related to structure parameters and material properties. In the present work, the effect of hydrodynamic lift characteristic on slipper bearing capacity is not presented in order to simplify the calculation process. The results of a series of parametric studies are presented to gain insight into the relationship among film temperature, slipper radius ratio, fixed damper length-diameter ratio, and slipper thermal conductivity. In order to investigate the slipper bearing capacity, the slipper structure and material parameters are listed in Table 1. The initial operating condition and lubricant characteristics, as input parameters, are listed in Table 2.

5.1 Model verification with experimental results

In order to validate the developed model with existing experimental results, thermal equilibrium clearance between swash plate and slipper over one shaft revolution is shown in Fig. 8. As expected, the thermal equilibrium clearance periodically changes with shaft rotational angle. The thermal equilibrium clearance is reduced from 5 μm to 3 μm due to the high squeeze film effect when fluid pressure in piston chamber increases from 0 to 21 MPa. As shaft rotational angle increases from 180° to 360°, the thermal equilibrium clearance increases from 3 μm to 4 μm due to low squeeze film effect when the fluid pressure decreases from 21 MPa to 0. It is important to point out that the experimental result shows an oscillation tendency compared with simulation result. This is as much evident as fluid hydrostatic effect and the amplitude of oscillations strongly decreases because of high axial pressure load exerted on the slipper.

Table 1 Slipper structure and material parameters

Table 2 Input parameters of model

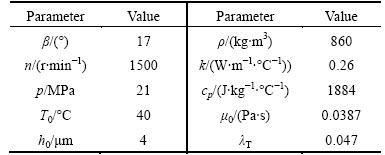
Fig. 8 Thermal equilibrium clearance of slipper/swash plate pair over one shaft revolution

To examine the influence of shaft rotational speed and fluid pressure on the thermal equilibrium clearance between slipper and swash plate, the comparison between experimental and simulation results due to the change in shaft rotational speed and fluid pressure is given in Table 3. It can be found that the thermal equilibrium clearance decreases obviously with the increase of fluid pressure or the decrease of shaft rotational speed. The reason is that the solid thermal deformation caused by film temperature, such as slipper and swash plate, increases rapidly due to high shaft rotational speed and fluid pressure. The overall result is a rather low decline in the thermal equilibrium clearance. The thermal equilibrium clearance difference is less than 1 μm compared with experimental result. The simulation result is believed to be sufficiently accurate for the present study, and the slipper bearing capacity can be analyzed based on this model.

Table 3 Comparison between measured and calculated results of thermal equilibrium clearance

Figure 9 shows temperature variations of slipper and swash plate parts over one shaft revolution. It can be observed that the solid temperature periodically changes with shaft rotational angle. The solid temperature increases from 43 °C to 49.2 °C when the fluid pressure increases from 0 to 21 MPa. The reason is that more heat generated by viscous friction between slipper and swash plate causes solid temperature to increase. As shaft rotational angle increases from 180° to 360°, solid temperature is decreased from 49.2 °C to 43 °C when the fluid pressure decreases from 21 MPa to 0. In addition, the solid temperature differential is less than 0.8 °C. As the solid temperature increases, surface deformation of slipper caused by solid temperature increases rapidly, and the overall result is a rather high decline in the thermal equilibrium clearance that may cause abrasion wear.

5.2 Effect of film temperature

In this work, the initial film thickness varies from  1 μm to 10 μm and the film temperature varies from 40 °C to 50 °C. Figure 10 shows relationship between thermal equilibrium clearance and film temperature. As expected, the minimum thermal equilibrium clearance decreases with increasing film temperature. When the film temperature is 50 °C and the initial film thickness varies from 1 μm to 4 μm, the minimum thermal equilibrium clearance decreases below 4.5 μm. The overall result is that slipper is unable to operate normally due to thin thermal equilibrium clearance in thermal steady state.

Fig. 9 Temperature calculations of slipper and swash plate parts over one shaft revolution

Fig. 10 Thermal equilibrium clearance and film temperature relationship

Figure 11 shows the relationship between slipper bearing capacity and film temperature. The slipper bearing capacity periodically changes with shaft rotational angle and increases as the film temperature increases. The physics phenomenon is related to the film stiffness that is defined as the gradient of slipper bearing capacity in the direction of film thickness. This film stiffness changes with different film temperature. As the thermal equilibrium clearance decreases, the bearing capacity for high film temperature increases faster than the low film temperature, implying that the film stiffness increases as the temperature increases. There are two factors that affect the slipper bearing capacity. They are the film thickness and the fluid viscosity. It can be found that the slipper bearing capacity decreases obviously with the increase of fluid pressure, but it will become higher as fluid viscosity increases. As the film thickness decreases, the film temperature increases rapidly, and the overall result is a rather high increase in the slipper bearing capacity.

Fig. 11 Slipper bearing capacity and film temperature relationship

5.3 Effect of fixed damper length-to-diameter ratio

As to the resistance of fixed damper at the slipper pocket, it increases rapidly with increasing the length-to- diameter ratio of fixed damper. At the high pressure and speed condition, the working fluid in piston chamber is injected through the fixed damper into slipper pocket, which generates support force and avoids the contact between slipper and swash plate. In these numerical simulations, three length-to-diameter ratios of fixed damper are tested: 3.5, 4.75, and 8.75. Figure 12 shows relationship between thermal equilibrium clearance and length-to-diameter ratio of fixed damper. The minimum thermal equilibrium clearance decreases dramatically as the length-to-diameter ratio of fixed damper increases from 3.5 to 8.75. Two factors contribute to this influence, the hydrostatic pressure and the pressure drop along the fixed damper. As length-to-diameter ratio of fixed damper increases, the hydrostatic pressure in the slipper pocket increases. At the same time, the thermal equilibrium clearance due to high squeeze film effect becomes thin.

Figure 13 shows relationship between slipper bearing capacity and length-to-diameter ratio of fixed damper. As the length-to-diameter ratio of fixed damper decreases from 3.5 to 8.75, the slipper bearing capacity decreases due to lower fluid pressure and the thermal equilibrium clearance becomes large, implying that the film stiffness decreases with decreasing the length-to- diameter ratio of fixed damper. Therefore, the length-to- diameter ratio of fixed damper is more suitable for being used as fixed resistance owing to its many advantages in improving slipper bearing capacity.

Fig. 12 Relationship between thermal equilibrium clearance and length-to-diameter ratio of fixed damper

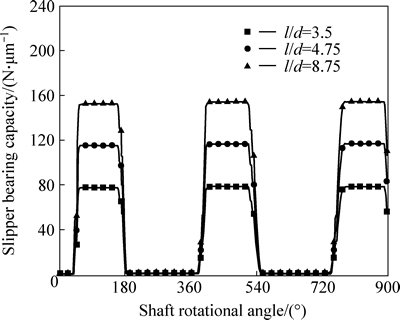
Fig. 13 Relationship between slipper bearing capacity and length-to-diameter ratio of fixed damper

5.4 Effect of slipper radius ratio

Figure 14 shows relationship between thermal equilibrium clearance and slipper radius ratio. It is clear that the minimum thermal equilibrium clearance decreases dramatically from 5.6 μm to 1.5 μm when the slipper radius ratio increases from 1.5 to 2. The reason is that the thermal equilibrium clearance is positively related to solid thermal deformation. There are two factors that affect the solid thermal deformation. They are solid temperature and heat flux. As the heat flux caused by viscous dissipation at the slipper/swash plate interface increases, solid thermal deformation increases with the increase of solid temperature. The overall result is that the minimum thermal equilibrium clearance decreases dramatically with the rise of solid thermal deformation.

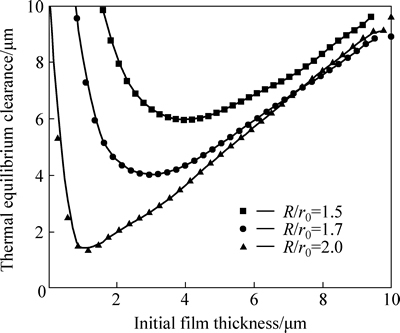
Fig. 14 Thermal equilibrium clearance and slipper radius ratio relationship

Figure 15 shows relationship between slipper bearing capacity and slipper radius ratio. It is clear that the slipper bearing capacity increases with increasing the slipper radius ratio. Comparing Figs. 14 and 15, it can be found that thermal equilibrium clearance increases with decreasing the slipper radius ratio, but slipper bearing capacity decreases with the decrease of slipper radius ratio. These results imply that if one desires a thin thermal equilibrium clearance, then higher slipper radius ratio may be used. If low viscous friction and abrasion wear at slipper/swash plate interface are preferred, then lower slipper radius ratio may be applied. The optimum selection of slipper radius ratio depends on the pump operating condition and can be found on a case by case basis.

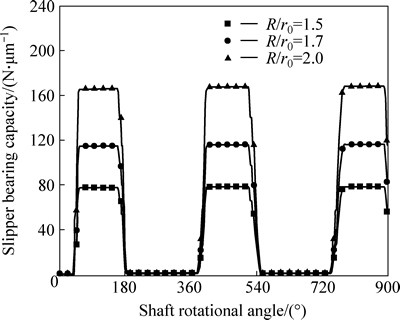
Fig. 15 Slipper bearing capacity and slipper radius ratio relationship

5.5 Effect of slipper thermal conductivity

Solid temperature is related to the slipper thermal conductivity that causes solid thermal deformation. Solid thermal deformation has great influence in thermal equilibrium clearance between slipper and swash plate. In these numerical simulations, three kinds of different materials are tested. They are 38CrMoAlA (k₁=57 W/(m·°C)), QT500-7 (k₁=67 W/(m·°C)) and ZCuSn10Pb11Ni3 (k₁=98 W/(m·°C)). Figure 16 shows relationship between thermal equilibrium clearance and slipper thermal conductivity. The result shows that the minimum thermal equilibrium clearance increases from 3.5 μm to 5 μm, while high slipper thermal conductivity is selected. It can be explained that thermal exchange between fluid film and solid parts is enhanced by high slipper heat conductivity and more heat fluxes are removed rapidly from slipper/swash plate interface. This leads to a further reduction in solid temperature and thermal deformation. The minimum thermal equilibrium clearance increases with the decrease of solid deformation.

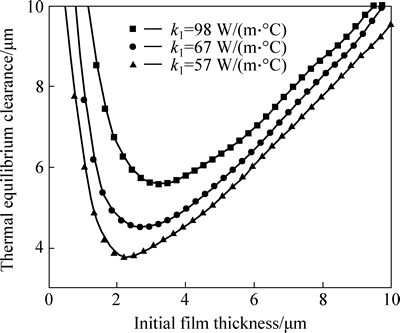
Fig. 16 Relationship between thermal equilibrium clearance and slipper thermal conductivity

Figure 17 shows relationship between slipper bearing capacity and slipper thermal conductivity. It is found that slipper bearing capacity increases from 81.9 N/μm to 65.2 N/μm, while the slipper thermal conductivity is decreased from 98 W/(m·°C) to 57 W/(m·°C). The reason is that thermal equilibrium clearance is related to solid thermal deformation. If heat flux can not be removed at the slipper/swash plate interface, the solid temperature increases dramatically as the slipper thermal conductivity decreases. Moreover, the thermal equilibrium clearance decreases as the rise of thermal deformation caused by solid temperature. It can be demonstrated that the higher slipper thermal conductivity, such as ZCuSn10Pb11Ni3, is useful to improve slipper bearing capability, but the minimum thermal equilibrium clearance is not compromised.

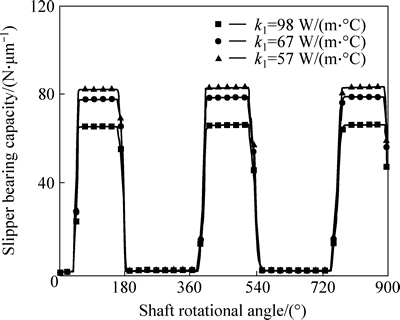
Fig. 17 Relationship between slipper bearing capacity and slipper thermal conductivity

6 Conclusions

1) The thermal model of hydrostatic slipper is developed to analyze thermal equilibrium clearance and slipper bearing capacity, which helps to reveal the principle of surface abrasion. The existing experimental test is in accordance with the simulation result to a great extent. The simulation model has a high accuracy and it can be used in the analysis and optimization of performance promotion for axial piston pump.

2) Thermal equilibrium clearance between slipper and swash plate due to solid thermal deformation periodically changes with shaft rotational angle. The thermal equilibrium clearance decreases obviously with the increase of fluid pressure or the decrease of shaft rotational speed. If the thermal equilibrium clearance decreases beyond the minimum value, slipper is unable to operate normally in thermal steady state. Slipper structure parameters and material properties are useful to improve slipper bearing capability, but thermal equilibrium clearance is not compromised.

3) However, only a simplified thermal model of hydrostatic slipper is presented, which is not adequate in complex condition. More accurate thermal model of slipper friction pairs considering tilting and hydrodynamic effect should be investigated, and the experimental validation should be conducted in the future.

References

[1] XU Bing, ZHANG Jun-hui, YANG Hua-yong. Investigation on structural optimization of anti-overturning slipper of axial piston pump [J]. Science China Technological Sciences, 2012, 55(11): 3011-3018.

[2] LIU Huan-long, KE Jian, WU Guo-zhi, YU Lan-ying. Research on the lubrication characteristics of water hydraulic slipper friction pairs [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2006, 220(10): 1559-1568.

[3] NIE Song-lin, HUANG Guo-hua, LI Yong-pin. Tribological study on hydrostatic slipper bearing with annular orifice damper for water hydraulic axial piston motor [J]. Tribology International, 2006, 39(11): 1342-1354.

[4] DU Jun, WANG Shao-pin, ZHANG Hai-yan. Layered clustering multi-fault diagnosis for hydraulic piston pump [J]. Mechanical Systems and Signal Processing, 2013, 36(2): 487-504.

[5] LIN Shuo, HU Ji-bin. Research on the tribo-dynamic model of slipper bearings [J]. Applied Mathematical Modelling, 2015, 39(2): 548-558.

[6] TANG He-sheng, YIN Yao-bao, LI Jing. Clearance leakage and friction torque of slipper pair in axial piston pump [J]. Journal of South China University of Technology: Natural Science Edition, 2014, 42(7): 75-79. (in Chinese)

[7] MANRING N D, JOHNSON R E, CHERUKURI H P. The impact of linear deformations on stationary hydrostatic thrust bearings [J]. Journal of Tribology, 2002, 124(4): 874-877.

[8] JOHNSON R E, MANRING N D. Translating circular thrust bearing [J]. Journal of Fluid Machines, 2005, 503(5): 197-212.

[9] WIECZOREK U, IVANTYSYNOVA M. Computer aided optimization of bearing and sealing gaps in hydrostatic machines-the simulation tool CASPAR [J]. International Journal of Fluid Power, 2002, 3(1): 7-20.

[10] KAZAMA T. Thermohydrodynamic lubrication model applicable to a slipper of swash plate type axial piston pumps and motors (effects of operating conditions) [J]. Tribology Online, 2010, 5(5): 250-254.

[11] KUMAR S, BERGADA J M, WATTON J. Axial piston pump grooved slipper analysis by CFD simulation of three dimensional NVS equation in cylindrical coordinates [J]. Compute & Fluids, 2009, 38(3): 648-663.

[12] BERGADA J M, WATTON J, HAYNES J M. The hydrostatic/hydrodynamic behaviour of an axial piston pump slipper with multiple lands [J] Meccanica, 2010, 45(4): 585-602.

[13] WANG X, YAMAGUCHI A. Characteristics of hydrostatic bearing/seal parts for water hydraulic pumps and motors. Part 1: experiment and theory [J]. Tribology international, 2002, 35(7): 425-433.

[14] WANG X, YAMAGUCHI A. Characteristics of hydrostatic bearing/seal parts for water hydraulic pumps and motors. Part 2: On eccentric loading and power losses [J]. Tribology international, 2002, 35(7): 435-442.

[15] CANBULUT F, KOC E, SINANOGLU C. Design of artificial neural networks for slipper analysis of axial piston pumps [J]. Industrial Lubrication and Tribology, 2009, 61(2): 67-77.

[16] MESGARNEJAD A, KHONSARI M M. On the tribological behavior of MoS₂-coated thrust ball bearings operating under oscillating motion [J]. Wear, 2010, 269(7/8): 547-556

[17] YIN Fang-long, NIE Song-lin, ZHANG Zheng-hua, ZHANG Xiao-jun. Research on the sliding bearing pair of water hydraulic axial piston pump [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Mechanical Engineering Science, 2013, 227(9): 2049-2063.

[18] KALIN M, MAJDIC F, PEZDIRNIK J, VELKAVRH I. Analyses of the long-term performance and tribological behavior of an axial piston pump using diamond like-carbon-coated piston shoes and biodegradable [J]. Journal of Tribology, 2008, 130(1): 011013-011020.

[19] ZHAO Xiao-yong, SUN Jun, WANG Chun-mei, WANG Hu, DENG Mei. Study on thermoelastohydrodynamic performance of bearing with surface roughness considering shaft deformation under load in shaft-bearing system [J]. Industrial Lubrication and Tribology, 2013, 65(2): 119-128.

[20] ANDHARIA P I, GUPTA J L, DEHERI G M. Effect of surface roughness on hydrodynamic lubrication of slider bearings [J]. Tribology Transactions, 2001, 44(2): 291-297.

[21] LI Cheng-gong, JIAO Zhong-xia. Thermal-hydraulic modeling and simulation of piston pump [J]. Chinese Journal of Aeronautics, 2006, 19(4): 354-358.

[22] ZOU Teng-an, XU Hai-jun, PAN Cun-yun, XU Xiao-jun, CHEN Hu. Mathematical modeling and analysis of thermodynamic processes in a twin-rotor piston engine [J]. Journal of Central South University, 2014, 21(11): 4163-4171.

[23] MA Xi-zhi, ZHU Jun. Experimental study of transient thermal elastic hydrodynamic lubrication of tilted thrust bearing under sudden load changes [J]. Journal of Harbin Institute of Technology (New Series), 2011, 6(6): 48-52.

[24] GLAVATSKIH S B, FILLON M, LARSSON R. The significance of oil thermal properties on the performance of a tilting-pad thrust bearing [J]. Journal of Tribology, 2001, 124(2): 377-385.

[25] HUANG Guo-qin, HE Xiao-feng, ZHU Yu-quan. Analysis on optimal clearance of piston friction pair and its influence factors for water hydraulic pump [J]. China Mechanical Engineering, 2011, 22(14): 1668-1672. (in Chinese)

(Edited by YANG Hua)

Foundation item: Projects(51475332, 51275356) supported by the National Natural Science Foundation of China

Received date: 2014-12-02; Accepted date: 2015-04-10

Corresponding author: Yin Yao-bao, Professor, PhD; Tel: +86-21-69589736; E-mail: y-yin@tongji.edu.cn