基于典型断面雨量-水位函数的中小桥水害预测

李整¹，文雨松¹，罗艺²，赵尊焘¹

 (1. 中南大学 土木建筑学院，湖南 长沙，410075；

2. 衡东县交通局，湖南 衡阳，421400)

摘  要：基于推理公式法和均匀稳定流概念，借助模糊相似优先比理论，提出一种针对既有中小桥的水害预测新方法。将实际中小桥河床断面归纳为10类典型断面，建立各类典型断面的雨量-水位函数模型；利用模糊相似优先比理论确定与实际断面最相似的典型断面，选取雨量-水位函数模型；借助可靠的墩台水痕和对应的雨量资  料，求解常量参数K，确定雨量-水位函数，再利用现时或预报雨量资料对桥梁抗洪能力进行评估和水害预测。研究结果表明：该方法的理论基础可靠，只需要桥址处河床糙率系数和一组历史雨量及对应的水痕标高数据，当地质情况已知时，还可以进行冲刷程度预测；避免了收集汇流方式、雨量损失、流域平均坡度、流域面积和主河槽长度等水文参数，减少了大量的野外勘测工作和繁琐的计算量；实例桥梁检测表明本方法使用方便，精度满足实际要求。

关键词：水害预测；雨量-水位函数；模糊相似优先比；水痕

中图分类号：U442.3         文献标志码：A         文章编号：1672-7207(2010)04-1597-07

Flood forecast method for middle & small bridges based on rainfall-water level functions of representative riverbed sections

LI Zheng¹, WEN Yu-song¹, LUO Yi², ZHAO Zun-tao¹

 (1. School of Civil and Architectural Engineering, Central South University, Changsha 410075, China;

2. Hengdong Communication Bureau, Hengyang 421400, China)

Abstract: Based on rational formula, homogeneous flow and fuzzy similar-priority comparison theory, a new flood forecast method for existing middle and small bridges was presented. Firstly, according to shapes of actual riverbed sections, riverbed sections were reduced to 10 types of representative riverbed sections, and rainfall-water level function model of every representative riverbed section was established. Then, using the fuzzy similar-priority comparison theory, the most similar section with actual section was found, so the function model could be got. Finally, by dint of reliable water marks on piers and the corresponding rainfalls, constant K was solved. Sequentially, rainfall-water level function could be fixed and instantaneous or forecast rainfall data could be used to assess flood-resistance performance and predict flood of bridges. The results show that this new method has credible theoretic foundation. Once roughness and a couple of rainfall and water mark at bridge sites are provided, prediction can be made. Besides, when geologic condition is known, scouring can be predicted too, avoiding fussy calculation and troublesome field reconnaissance in order to collect parameters, such as ways of runoff confluence, loss of rainfall, average gradient and area of drainage basin, length of main river course, and so on. This method is easy to use and its degree of accuracy can meet the actual demand.

Key words: flood forecast; rainfall-water level function; fuzzy similar-priority comparison; water marks

洪水水毁是世界各国桥梁共同面临的严重自然灾害^[1]。对美国1989—2000年毁坏的500座桥梁进行分析发现：洪灾和撞击引起桥梁失事频率最高，仅1993年洪水和冲刷毁坏的桥梁所占比例就高达53%^[2]。我国桥梁设计规范经历了数次修改，按照不同规范设计的桥梁的抗洪能力很可能不在同一水平上。建桥后河道的水流改变，破坏了河床的输沙平衡，引起河床冲刷^[3-4]；多年的人类活动和自然演变，流域内大地植被也发生了较大变化；河道上的非法建筑、非法挖沙等都有可能影响既有桥涵的过洪能力。此外，近年来我国大多数地区气候反常，降雨量时空分布不均，暴雨活动范围广，强度大，局部地区洪涝严重。桥梁作为跨河构造物，直接遭遇洪水的冲击，一旦发生水毁，将给铁路、公路运输生产带来严重的损失^[5]。因此，按现时桥梁所处的水文环境，对既有桥梁重新进行抗洪能力评估显得很有必要。目前，洪水预测的研究已将水文学知识及它们之间的联系进行考虑，不再局限于对观测洪峰资料进行简单统计评价^[6]。河道洪水水位的预报方法有多种，如采用水文学方法得到预报流量值，再由水位流量关系曲线得到预报水位和动力波模型等，但这些方法均需要预报断面的流量和水位资料，对无流量观测的水位站则无法应用^[7]。由于很多中小桥没有设置专门的水文观测站，很难用形态勘测方法或流量观测资料推算检定流量，因此，现行中小桥水文检定普遍采用从雨量到流量的方法，它们基本上属于推理公式法、单位线法或经验公式法。采用现行方法对既有桥梁进行水文检定时，大多需要汇流方式、雨量损失和主河槽长度等参数。在缺少资料和无资料地区，虽然有研究表明，水文参数可以应用回归方程或者采用有实测资料的相似流域资料进行估   算^[8-9]，但是，这使得参数的确定更加麻烦。基于上述原因，本文作者提出一种基于雨量-水位函数的中小桥水害预测的新方法。利用既有桥梁墩台上的水痕和对应的暴雨资料，确定桥址处的雨量-水位函数，进而通过搜集到的实时雨量或预报雨量资料进行水害预测。这一方法对于中小流域桥梁特别是对于缺少水文资料的中小桥水害预测具有重要的理论意义与实践  意义。

1  中小桥雨量-水位函数模型

1.1  流量计算

推理公式法认为计算流量Q_p与频率为p的暴雨强度a_p和流域面积F的乘积成正比^[10]，即：                              

               (1)

式中：Q_p为通过桥址处河床断面频率为p的计算流量，m³/s；0.278为流量和雨量强度单位统一时的乘子；为比例系数，与汇流方式、雨量损失、流域坡度和主河槽长度等因数有关；a_p为桥梁汇流面积内频率为p的暴雨强度，mm/h；F为流域面积，km²。

汇流后能够引起桥址处高水位的暴雨，其汇流方式、汇流过程中的雨量损失差别小；1座桥梁所在流域的流域面积、流域坡度和主河槽长度等流域参数不随雨量变化，因此，可以认为比例系数和流域面积F基本不变。另外，对于1场确定的暴雨，雨量和流量都与频率无关，因此，式(1)可以简写为

                   (2)

式中：Q为计算流量；A_k为常量参数(为0.278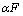)；a为暴雨强度。

大多数桥址处的河道常能近似地形成稳定均匀 流^[11]。流量计算公式为

            (3)

式中：Q为计算断面的流量；n为糙率；I为水力坡度；ω为过水断面面积；x为湿周。

1.2  雨量-水位函数模型的建立

令，联立式(2)和式(3)，可得单式断面对应的雨量-水位函数为： 

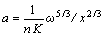           (4)

对于河床断面明显分成左河滩、主槽和右河滩三部分的复式断面，对应的雨量-水位函数为：

           (5)

式中：n_i，ω_i和x_i分别为河床断面各部分(i=1代表左河滩；i=2代表河槽；i=3代表右河滩)的糙率、过水断面面积和湿周。

式(4)~(5)表明：暴雨强度a和水位H的关系与过水断面面积ω和湿周x有关。ω和x关于H的函数形式与河床断面形状有关，而自然界中河床断面形态千差万别。为避免对每座桥梁进行雨量-水位函数的繁琐推导，并得到比较统一的函数形式，本文作者通过对实际河床断面进行分析与简化，将实际河床断面归纳为10种典型断面，预先建立各典型断面的雨量-水位函数，应用时基于实测河床断面对其进行选择，不再需要重复推导。各典型断面示意图如图1所示。
 

图1  典型断面示意图

Fig.1  Sketches of representative riverbed sections

对于图1(a)所示典型断面，令，，则：

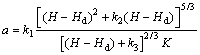         (6)

式中：H为水位；H_d为河床最低点高程；k₁，k₂和k₃为与断面尺寸、糙率有关的常量参数，其中，，，。

对于图1(b)所示典型断面，假设曲线段线形为抛物线，令，，则：

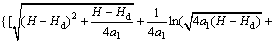
 (7)

式中：

；

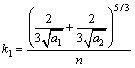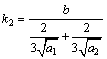
同理可得其他典型断面对应的雨量-水位函数。

对图1(c)所示典型断面，有

+

对图1(d), (e), (g)和(i)所示典型断面，有

对图1(f)所示典型断面，有

对图1(h)和(j)所示典型断面，有

式中：k₁，k₂，k₃，k₄，k₅，k₆，k₇，k₈，a₁，a₂和H_t(H_t=H_d-h₀)等是与断面尺寸、糙率系数和河滩高程有关的参数，为已知量；K可以利用历史雨量和水痕资料^[12]求出，为待求量。

2  典型断面的模糊相似优先对比分析

以上得到6种雨量-水位函数模型，选用的雨量-水位函数模型是否与实际河床断面最接近，可通过判断典型断面和实际断面的相似程度来实现。表征实际断面和典型断面的因素有多个，在各因素相似程度不同的多个断面中选择1个最佳断面，使其能从多因素上综合反映实际断面的特征。这是引入模糊相似优先比进行优先相似排序的目的。

2.1  模糊相似优先比

模糊相似优先比是以成对的样本与1个固定的样本作比较，确定哪一个与固定样本更相似^[13-14]。假定样本x_i和x_j与固定样本x_k进行比较，其相似优先比为r_ij，x_i与x_j的优先判定为：

(1) 若r_ij∈(0.5, 1.0)，则表示x_i比x_j优先。

(2) 若r_ij∈(0, 0.5)，则表示x_j比x_i优先。

(3) 3种极值情形：若r_ij=1，则表示x_i比x_j显然优先；若r_ij=0，则表示x_j比x_i显然优先；若r_ij=0.5，则表示x_i和x_j等价，优先无法确定。

另外还假设：

(1) 0≤r­_ij≤1，且r_ii=1；i, j=1, 2, …, n；

(2) r_ij+r_ji=1, i≠j; i, j=1, 2, …, n。

若采用海明(Haiming)距离作为相似优先比中r_ij的测度，则对样本x_i和样本x_j与固定样本x_k进行比较，r_ij可定义为：

式中：；。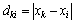

对给定的样本集合X={x₁, x₂, …, x_n}和固定样本x_k，令任意x_i, x_j∈X和x_k进行比较，计算两样本间的相似优先比，从而得到模糊相似优先比矩阵R：

建立模糊相似矩阵之后，一般根据r_ij的大小，由λ水平评出相似程度，计算出相应的矩阵R_λ：

  式中：, 。

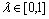在λ下降过程中，将首先出现λ₁，使R_λ中第i₁行元素全部为1，对于特定目标样本x_k，x_i1是第一优先相似元素。删除R_λ中第i₁行和i₁列，得到新的(n-1)×(n-1)模糊相似优先比矩阵，降低λ，同样的方法获得x_i2，得到新的(n-2)×(n-2)模糊相似优先比矩阵，依此类推，处理完截矩阵，即可依次排出全部待选样本与目标样本x_k的相似次序。

2.2  最相似断面的选取

若每个样本有m个因素，则每个因素都有1个对应的模糊相似优先比矩阵，每个样本的每1个因素都将产生1个反映相似程度的序号，将各个因素的序号相加，其结果即为该样本与固定样本相似程度的综合反映。样本的序号越小，表明与固定样本越相似。文中实际断面为固定样本，记为A₀；10种典型断面为样本集X=｛A₁，A₂，A₃，A₄，A₅，A₆，A₇，A₈，A₉，A₁₀｝。选用的主要因素集为：{C₁, C₂, C₃, …, C₇}，其中：C₁为左河滩面积；C₂为左河滩湿周；C₃为河槽面积；C₄为河槽湿周；C₅为右河滩面积；C₆为右河滩湿周；C₇为平均水深。

3  实例

3.1  京广线金鸡湾桥

表1所示为该桥历史雨量和水位记录，表2所示为河床标高。左河滩、河槽和右河滩的糙率分别为1/12，1/20和1/12。河床地质情况：标高67.3 m以上是粒径为10 mm的圆砾石，标高67.3~65.1 m是粒径为20 mm的小卵石，标高65.1~58.7 m是粒径为100 mm的大卵石。

基于差值最小原则确定典型断面的尺寸，并对典型断面进行模糊相似优先比排序，主要因素对比结果如表3所示，相似程度排序结果如表4所示。

从表4可以看出：典型断面6(A₆)与桥址处的河床断面最相似，断面对比图如图2所示。

表1 日最大暴雨量与水位表

Table 1  Relationships between maximal 24 h rainfalls and water levels

表2  河床标高

Table 2  Riverbed elevation

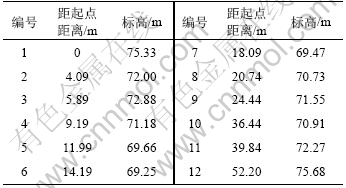
表3  典型断面主要因素比较

Table 3  Comparisons of main factors of representative riverbed sections

表4  A₁～A₁₀对A₀的相似程度

Table 4  Similarity between A₀ and A₁～A₁₀

图2  典型断面6与实际断面对比图

Fig.2  Comparison between representative riverbed section 6 and actual riverbed section

图1(f)所示典型断面的几何尺寸为：b₁=5.250 m，b₂=5.250 m，b₃=3.500 m，b₄=15.750 m，b₅=3.500 m，b₆=4.370 m，b=6.125 m，h₀=2.300 m，h₁=3.780 m，H_d=69.250 m。计算各参数值分别为：k₁=4.567，k₂=264.415，k₃=4.567，k₄=5.040，k₅=2.045，k₆=1.653，k₇=22.680，k₈=9.203。故该桥对应的雨量-水位函数为：

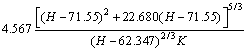
将表1中数据代入上式，得K=22.319。查水文手册得该桥流域中心日暴雨量百年一遇强度a_p= 217.5 mm，反算得桥址水位H_p=74.507 m。值得注意的是，本研究所得到的函数解是建立在既有桥梁的条件上，得到的H_p包含了桥前壅水高度和风浪高度。经计算，桥下浪高为0.120 m，桥前壅水高度为0.140 m，则桥下静水位为(74.507-0.140-0.120) m=74.247 m。传统的推理公式法计算的静水位为74.230 m，可见：采用本文研究方法所得计算结果与采用传统方法所得计算结果的差别较小。

水位确定后，由一般冲刷公式和局部冲刷公式修正式^[15]可计算得到基础冲刷情况：一般冲刷后的最大水深h_p=6.95 m；局部冲刷深度h_b=1.76 m。

以上输入的雨量数据是从当地水文手册中查到的设计频率对应的24 h暴雨强度，计算结果为设计洪水发生时的水害情况；当输入的雨量是雨量站即时雨情时，计算结果即为即将到达桥址处的结果。

3.2  沪昆线占卜桥和泰肥线滂河桥

通过运用与金鸡湾桥相同的计算过程，可得到占卜桥与滂河桥的计算结果。占卜桥原设计流量Q_p=   523 m³/s。使用单位线法得其百年一遇的流量Q_p1=521 m³/s；使用本文作者提出的方法得其百年一遇流量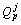=517 m³/s，由本文方法与传统方法所得的结果比较接近。

滂河桥原设计流量Q_p=910 m³/s。使用单位线法得其百年一遇的流量Q_p1=910.6 m³/s，按照铁四院使用的计算方法求得其百年一遇的流量Q_p2=936.6 m³/s；使用本文作者提出的方法得百年一遇流量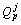=918.1 m³/s，与单位线法所得的结果比较接近。

4  结论

(1) 雨量-水位函数模型是在推理公式法和均匀稳定流的基础上建立的，基础理论可靠，满足均匀稳定流条件的中小流域桥梁均可采用本文作者提出的方法进行水害预测。

(2) 雨量-水位函数模型利用墩台水痕和历史雨量资料确定既有桥梁的雨量水位关系，计算得到的水位资料包含了壅水高度和波浪高度，不需要再加壅水高度和波浪高度。

(3) 预先建立了10种典型断面的雨量-水位函数模型，应用时只需基于实测河床断面对其进行选   择，不需要重复推导，方便计算机编程实现。特别是应用于多座桥梁时，可减少大量的重复性工作。

(4) 本文作者提出的水害预测方法，只需要收集桥梁河床断面、糙率系数和历史雨量及对应的水痕高程即可进行水位预测；当河床地质情况已知时，还可以进行冲刷方面的预测。与现行方法相比，它避免了收集汇流方式、雨量损失、流域平均坡度、主河槽长度和流域面积等参数，减少了大量的野外工作，使用方便，且精度满足实际需要。

参考文献：

[1] Bruce B. Analyzing bridge failures[J]. Materials Performance, 2008, 47(6): 95-95.

[2] Wardhana K, Hadipriono F C. Analysis of recent bridge failures in the United States[J]. Journal of Performance of Constructed Facilities, 2003, 17(3): 144-150.

[3] 文超, 文雨松. 漂石河床扩大基础桥墩局部冲刷深度的人工神经网络解[J]. 中南大学学报: 自然科学版, 2004, 35(2): 333-336.
WEN Chao, WEN Yu-song. The artificial neural network method used to calculate the depth of local scour of the expending base piers in the boulder riverbed[J]. Journal of Central South University: Science and Technology, 2004, 35(2): 333-336.

[4] 文超, 文雨松. 漂石河床一般冲刷的人工神经网络解[J]. 铁道学报, 2004, 26(1): 93-95.
WEN Chao, WEN Yu-song. Solution of the artificial neuron network to general scouring in the boulder riverbed[J]. Journal of the China Railway Society, 2004, 26(1): 93-95.

[5] 李海瑞. 桥梁水毁的预防与治理[J]. 公路, 2007(7): 209-211.
LI Hai-rui. Prevention and treatment on damage to bridges by flood[J]. Highway, 2007(7): 209-211.

[6] Merz R, Bloschl G. Extended information basis for the determination of flood probabilities[J]. Hydrologie Und Wasserbewirtschaftung, 2008, 52(6): 300-309.

[7] 王光生, 宁方贵, 肖飞, 等. 实用水文预报方法[M]. 北京: 中国水利水电出版社, 2008: 1-55.
WANG Guang-sheng, NING Fang-gui, XIAO Fei, et al. Hydrological prediction method[M]. Beijing: China Water Conservancy and Hydropower Press, 2008: 1-55.

[8] 谈戈, 夏军, 李新. 无资料地区水文预报研究的方法与出路[J]. 冰川冻土, 2004, 26(2): 192-196.
TAN Ge, XIA Jun, LI Xin. Hydrological prediction in un gauged basins[J]. Journal of Glaciology and Geocryology, 2004, 26(2): 192-196.

[9] 柴晓玲. 无资料地区水文分析与计算研究[D]. 武汉: 武汉大学水文学及水资源学院, 2005: 18-28.
CHAI Xiao-ling. Hydrologic estimation method and analysis in un-gauged basins[D]. Wuhan: Wuhan University. School of Hydrology and Water Resource, 2005: 18-28.

[10] 文雨松. 桥涵水文[M]. 北京: 中国铁道出版社, 2005: 83-87.
WEN Yu-song. The hydrology of bridges and culverts[M]. Beijing: China Railway Press, 2005: 83-87.

[11] 铁道部第三勘测设计院. 桥渡水文[M]. 北京: 中国铁道出版社, 1993: 41-43.
The Third Railway Survey and Design Institute. The hydrology of bridges and culverts[M]. Beijing: China Railway Press, 1993: 41-43.

[12] 曹二星, 文雨松. 基于桥墩水痕采用水位单位线预测既有中小桥水位[J]. 铁道建筑, 2008(9): 22-24.
CAO Er-xing, WEN Yu-song. Flood forecast for existing middle & small span bridges with unit hydrograph based on water trace on piers[J]. Railway Engineering, 2008(9): 22-24.

[13] 谢季坚, 刘承平. 模糊数学方法及其应用[M]. 武汉: 华中科技大学出版社, 2006: 130-143.
XIE Ji-jian, LIU Cheng-ping. Fuzzy mathematic methods and applications[M]. Wuhan: Huazhong University of Science and Technology Press, 2006: 130-143.

[14] 王顺洪. 用模糊相似优先比关系预测工程项目投标报价[J]. 西南交通大学学报, 2001, 36(1): 96-99.
WANG Shun-hong. Forecasting the bid of engineering projects with fuzzy similar-priority comparison[J]. Journal of Southwest Jiaotong University, 2001, 36(1): 96-99.

[15] TB 10017—99, 铁路工程水文勘测设计规范[S].
TB 10017—99, Design specifications for water survey in railway engineering[S].

收稿日期：2009-08-11；修回日期：2009-11-05

基金项目：山东省交通科技项目(2008X012)

通信作者：李整(1982-)，女，河南驻马店人，博士研究生，从事桥涵水文研究；电话：15073162564；E-mail: lizhengcsu@126.com

(编辑 刘华森)