DOI: 10.11817/j.issn.1672-7207.2016.08.012

三维织造复合材料细观模型

师有玲，单忠德，刘丰，陈思思，康怀镕

(机械科学研究总院 先进成形技术与装备国家重点实验室，北京，100083)

摘要：以三维织造复合材料为对象，结合三维织造缠绕路径，建立三维织造复合材料细观结构分析模型，推导纤维体积分数与细观模型结构参数之间的数学关系。研究导向套直径、导向套中心距等结构参数对纤维体积分数的影响。研究结果表明：结合PAN基碳纤维T300实验研究发现纤维体积分数相对误差可控制在5%以内。通过合理的结构设计和纤维规格匹配，三维织造复合材料可达到满意的纤维体积分数和弹性模量。当PAN基碳纤维T300三维织造复合材料的导向套半径为1 mm时，导向套中心距在4~6 mm之间对纤维体积分数的变化最敏感，中心距从4 mm增加到6 mm时导向套的纤维体积分数从19.63%下降到10.19%；当导向套半径控制在2 mm以内时，导向套中心距建议选取4~6 mm之间，可有效提高纤维体积分数；导向套半径为1 mm时，6K纤维与6 mm中心距配合能达到最大限度的利用结构体积单元空间。

关键词：三维织造；复合材料；细观模型；纤维体积分数；结构参数

中图分类号：TB332             文献标志码：A         文章编号：1672-7207(2016)08-2621-08

3D weaving composites microstructure model

SHI Youling, SHAN Zhongde, LIU Feng, CHEN Sisi, KANG Huairong

(State Key Laboratory of Advanced Forming Technology & Equipment,

China Academy of Machinery Science & Technology, Beijing 100083, China)

Abstract: The 3D weaving composites were the research objects, combined with the 3D weaving winding path, microstructure model of the composite material was formed, and the relationship between the fiber volume fraction and the parameters of microstructure model was derived. The effect of structure parameters, such as the center distance of the guide sleeves and the radius of guide sleeves, on fiber volume fraction was also studied. The results show that combined with the experimental research of the PAN-based carbon fiber T300, the relative error of fiber volume fraction is less than 5%. By rational structural design and optimistic matching of fiber specification, the 3D woven composite has the satisfying fiber volume fraction and elasticity modulus. When the radius of guide sleeves of the PAN-based carbon fiber T300 is 1 mm, the center distance of the guide sleeves between 4 mm to 6 mm is the most sensitive to the change of fiber volume fraction. The fiber volume fraction decreases from 19.63% to 10.19% with the increase of center distance from 4 mm to 6 mm. When the radius of pre-buried guide sleeves are less than 2 mm, the center distance of guide sleeves should be between 4 mm and 6 mm so that the fiber volume fraction can be effectively increased. When the radius of guide sleeves is 1 mm, the structure volume unit can be made the best by the combination of 6K fiber and the center distance of 6 mm.

Key words: 3D weaving; composites; microstructure model; fiber volume fraction; structure parameter

复合材料作为一种新型材料，经过近几十年来的快速发展，已经成为与金属材料、无机非金属材料、高分子材料并列的四大材料体系之一。复合材料由于具有低密度、高比强度、高比模量、良好的损伤容限和可设计性，在众多领域都有着广泛应用，特别是在航空航天、武器系统以及汽车制造等领域，对现代科技的发展有着重要的作用^[1-3]。复合材料三维织造是根据零部件结构特点进行分层扫描并按照一定的设计规则、间隔将织造导向套预埋在数字化导向模板上，再将丝材进行层层织造，直到整个预制件的织造完成。此方法创新性的实现了复合材料制备和零部件三维结构成形一体化，是一种新的复合材料成形技术，是传统复合材料成形的重大突破^[4-6]。复合材料三维织造实现了导向套的预埋，在增强层间剪切强度和分层阻抗的同时又避免了Z-pin中植入刚性夹杂(Z向销钉)对纤维的损伤，更能适应社会发展对复合材料近净成形技术的需求^[7]。但由于三维复合材料的各向异性、非均匀性、细观结构的复杂性，迄今为止，许多研究者提出了多种细观模型，解决了一些工程应用实际问题，但还不足以形成完善而统一的标准和结论。马文锁  等^[8]将基于细观结构模型的物理性能研究和力学性能研究归纳为三维编织复合材料理论分析中的2个关键问题，而纤维体积分数是物理性能研究的最主要参数。因此，首先必须建立细观模型，进而分析细观结构参数对三维织造复合材料纤维体积分数的影响。为满足工程实际应用需求，三维复合材料从最初的大幅度等效简化模型如单胞立方体织物模型(FGM)^[9]、“米”字型单胞模型、纤维倾斜模型(fiber inclination model)^[10]，到DU等^[11-13]提出的代表性单胞划分，再到冯伟等^[14-18]的纤维轨迹和横截面形状的模拟，以及朱元林等^[19]对纤维束之间相互挤压变形方式的建模研究，三维复合材料的细观结构研究已经从最初的大单胞逐步过渡到复杂的多胞体，再到精细的纤维真实形态的研究，已取得较为成熟的技术成果^[20]。由于编织复合材料力学性能主要取决于编织方法，而细观模型的建立也依赖于编织方法^[21]，经典的四步法、二步法织造过程变化能力是有限的，为了开发出性能更加优异的三维复合材料，越来越多的研究人员将目光投入到复合材料的优化设计和新织造工艺的开发上^[22]，三维织造即是一种全新的织造工艺，为三维复合材料的可设计性指明了新方向^[23-24]。本文作者在此基础上给出三维织造复合材料细观分析模型，建立纤维体积分数与细观模型结构参数的关系式，探讨结构参数对纤维体积分数的影响，为进一步优化三维织造复合材料力学性能提供建议，进而推动三维织造复合材料的设计与应用。

1  三维织造复合材料成形工艺

三维织造复合材料成形方法不同于传统织机编织方法，其成形原理如图1所示，首先对零件三维结构进行CAD模型分层，然后根据零件特点和轮廓信息进行数字化导向模板设计，按照一定规则、间隔将织造导向套布置在可控数字化模板上，纤维以导向模板上的点阵为节点进行层层织造，直到整个预制件的织造完成，最后预制件经压实后进行浸渍得到三维织造复合材料。

本文三维织造复合材料成形过程中导向模板的点阵布局采用四边形排布、纤维直线型缠绕。导向模板点阵排布完成后，织造纤维首先沿导向套间隙完成0°方向缠绕，然后通过过渡路径(图2中的虚线部分)依次过渡到45°，90°和-45°方向缠绕，即完成1个织造循环，按照上述步骤，再进行下一个织造循环，直到预制件织造完成，最终形成[0°/45°/90°/-45°]_S织造结构。织造成形过程如图2所示。

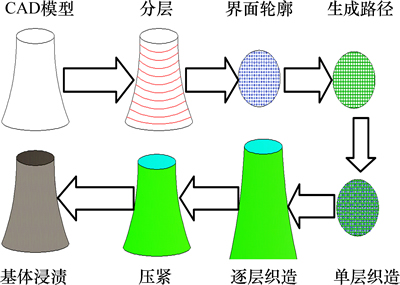
图1  三维织造方法基本流程图

Fig. 1  Basic flowchart of 3D weaving method

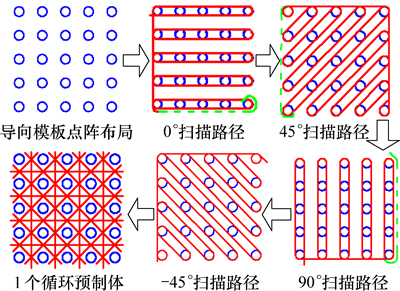
图2  织造过程示意图

Fig. 2  Diagram of weaving process

2  三维织造复合材料细观模型的建立

2.1  细观模型假设和单元胞体选取

针对三维织造复合材料细观模型结构本文进行以下假设：1) 预制件中的纤维为同一种型号；2) 纤维在预制件中都处于完全伸直状态；3) 纤维束的截面为矩形且沿纤维轴向截面形状保持不变；4) 变换织造角度时过渡路径纤维忽略不计；5) 纤维缠绕在导向套的表面。由于织造路径的周期性与对称性，因此，可以通过选取具有代表性的体积单元即单元胞体来研究其整体织造几何特征。本文所建立的单元胞体共2种：基元和边元。基元是在预制件内部选取，边元是在预制件的边缘选取。根据不同织造路径的边界纤维空间走向的不同，得到3组不同的边元：第一组边元中仅包含0°和90°织造纤维束，第二组和第三组边元中包含0°，45°，90°和-45°织造纤维束，基元与边元的空间结构形式如图3所示。

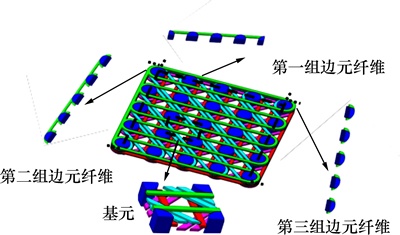
图3  单元胞体基元、边元示意图

Fig. 3  Diagram of primitive and repeated unit at edge area of cell

2.2  预制件中所有基元纤维体积

预制件导向套行数为m，列数为n，纤维束捻集率为k，织造纤维取N股，选取基元作为研究对象，如图4所示，基元内导向套中心距为a。依据上述织造工艺，在预制件内部，每0°/45°/90°/-45°为1个织造循环，设1个织造循环后预制件内所有基元包含的纤维长度L_I为

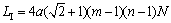        (1)

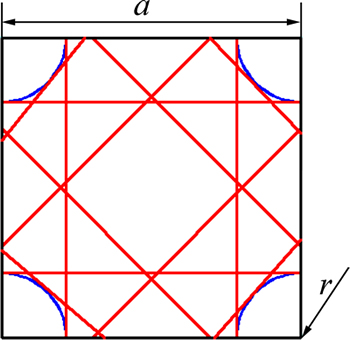
图4  基元示意图

Fig. 4  Sketch map of primitive

依据假设织造纤维束的截面形状为矩形，设单束纤维束的宽度为w，厚度为t，织造纤维束横截面积S为

S=wt                  (2)

则经过λ循环后预制件内所有基元包含的纤维体积V_I为

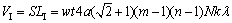   (3)

本文所用导向套由纤维和乙烯基树脂组成，形状为不同直径的圆柱体，则经过λ循环后预制件内所有基元包含的导向套纤维体积V_LI为

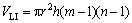             (4)

其中：h为实验测得的预制件实际高度；r为导向套半径。

2.3  预制件中所有边元纤维体积

图2中预制件0°路径4个边界中1个边界属于第二组边元纤维，1个边界属于第三组边元纤维，另2个边界属于第一组边元纤维，第一、二、三组边元纤维二维图如图5所示，1个循环后0°织造路径所有边元纤维的长度L_S11为

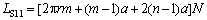     (5)

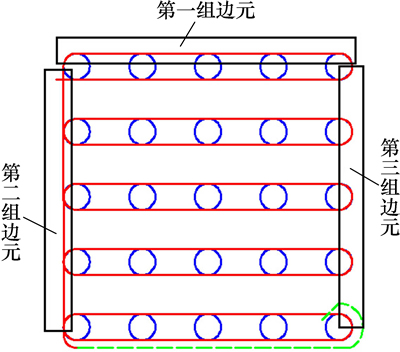
图5  织造边元纤维排布

Fig. 5  Distribution of brim fiber

经过λ循环后预制件0°织造路径的边元纤维的体积V_S11为

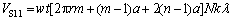   (6)

90°织造路径中边元纤维缠绕看作预制件0°方向旋转90°后形成的，经过λ循环后，预制件90°织造路径的所有边元纤维体积V_S12为

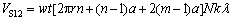   (7)

预制件45°织造路径边界纤维空间结构中有2个边属于第二组(见图2)，假设其中一边为(n-1)a+πrm，预制件关于45°对角线对称，另一边为(m-1)a+πrn；另外两边属于第三组，呈对称关系，其中一边为πrm，另一边为πrn；去掉4个角上重复计算的缠绕纤维4πr，所以预制件中45°织造路径一个循环的所有边元纤维长度L_S21为

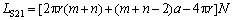   (8)

经过λ循环后预制件45°织造路径的所有边元纤维体积V_S21为

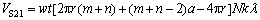  (9)

-45°织造路径关于45°织造路径镜面对称，经过λ循环后预制件纤维体积V_S22为

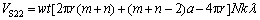  (10)

经过λ循环后预制件所有边元内的纤维体积V_S为

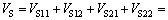
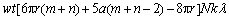   (11)

经过λ循环后预制件中所有边元包含的导向套的纤维体积V_LS为

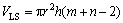          (12)

2.4  预制件纤维体积分数

预制件内所有导向套中的纤维体积V_L为

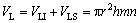        (13)

由于边界重复单元的存在，边元纤维会缠绕到最外层导向套之外，经过多次试验验证，预制体长度方向和宽度方向应分别增加1的余量，则预制件的总体积V为

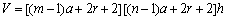   (14)

预制件中总纤维体积为所有基元、边元、导向套中纤维体积之和，则预制件的总纤维体积分数理论值φ_ft为

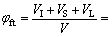
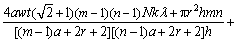
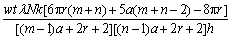   (15)

3  细观模型的校验

选取江苏恒神生产的PAN基碳纤维T300系列，规格为6K，原丝直径为7 μm，一束纤维有6 000根原丝，因此，取横截面积w×t=0.23 mm²，纤维密度ρ=1.7 g/cm³，用单股T300-6K纤维进行织造，缠绕18个循环，行数m=3，列数n=9，纤维束捻集率k=0.91，h的取值由实际测量得到，将各织造参数代入式(15)，经过计算可得到预制件总纤维体积分数的理论值φ_ft。实际值采用称重法，实验所用纤维质量为m，样品的实际纤维体积分数φ_fr为

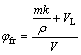                (16)

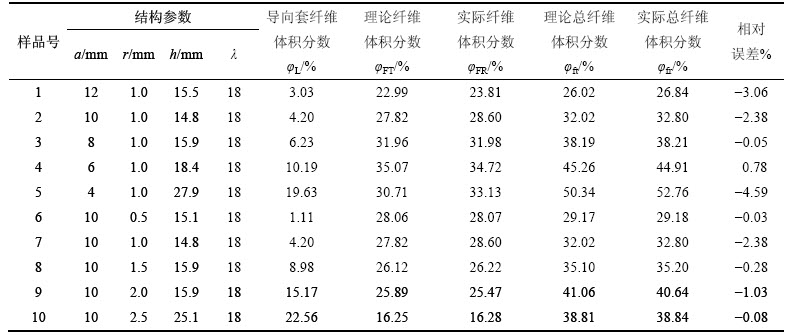
预制件样品如图6所示，样品的结构参数与纤维体积分数的理论值、实际值分别如表1所示。

图6  预制件试验样品

Fig. 6  Experimental sample of preform

由表1可以看出：纤维体积分数计算值与实际测量值相对一致，相对误差可控制在5%以内，验证了理论模型的合理性和建立的纤维体积分数与结构参数数学模型的准确性。但同时也发现，样品1号和5号的实际值与理论值之间存在一定的差别，造成实际值偏大的原因主要有：1) 模型假设的理想化，如假设纤维在预制体中处于完全伸直状态，沿纤维轴向截面形状保持不变，而在实际缠绕中由于张力不均匀使得纤维处于松弛或者挤压状态；由于本文假设纤维全部缠绕在导向套表面，纤维变换角度时过渡路径的纤维忽略不计，然而在实际缠绕中只有第1层是全部缠绕在导向套表面，连续纤维的缠绕变换织造路径时不可避免会多缠一些纤维；2) 试验过程中不可避免的人工误差。

表1  样品的织造参数与纤维体积分数

Table 1  Weaving parameter and fiber volume fraction of samples

4  结构参数对纤维体积分数的影响

合理的结构参数设计是实现复合材料工艺设计的关键工序之一，三维织造复合材料主要结构参数包括导向套中心距、导向套半径、编织方式。本文通过试验测试，研究了结构参数对三维织造复合材料纤维体积分数的影响。

本文所有实验中，纤维型号、导向套行数与列数均保持不变，图7(a)、图8(a)和图9(a)所示为表1中1~5号样品的导向套中心距与纤维体积分数的关系，这5种样品导向套的半径为1 mm；图7(b)、图8(b)和图9(b)所示为表1中6~10号样品的导向套半径与纤维体积分数的关系，这5种样品导向套中心距为10 mm。

由图7(a)可知：导向套中心距从4 mm增加到6 mm时，预制件中，导向套中的纤维体积分数变化幅度最大，从19.63%下降到10.19%，下降了大约57%，当导向套中心距在4~6 mm之间时对纤维体积分数的变化最敏感；由图7(b)可知：随着导向套半径的增大，导向套的纤维体积分数变化幅度比较均匀，呈现稳定增加。

由图8(a)可知：随着导向套中心距的增大，纤维体积分数先增大后减小，在中心距为6 mm时理论分析值与试验测试值中纤维体积分数均出现最大值分别为35.07%和34.71%，6 K纤维的几何参数在导向套半径选取1 mm，中心距选取6 mm时是最佳的匹配关系，即这时的纤维规格能够最大限度的利用此时的结构体积单元空间。但当导向套中心距继续增大，纤维体积分数直线下降，从而预制体内的纤维曲屈程度减小，导致弹性模量在一定程度上反而会增大；另外，随着导向套中心距的增大，预制件的浇注会更充分，更易获得较好性能的三维织造复合材料。由图8(b)可知：随着导向套半径的增大，纤维体积分数先小幅下降，此时导向套半径对纤维体积分数无显著影响；但当导向套半径大于2 mm时，纤维体积分数降幅非常明显，当半径从2 mm增加到2.5 mm时，所对应的实际纤维体积分数从25.47%下降到16.28%，下降了78.00%。由分析可知：通过合理的结构设计，选取最佳的纤维规格匹配，可达到满意的纤维体积分数和弹性模量。

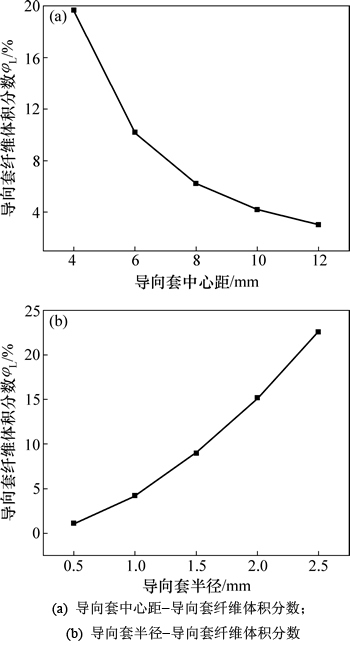
图7  导向套中心距、导向套半径与导向套纤维体积分数的关系

Fig. 7  Relationship among center distance of guide sleeves and radius of guide sleeves and guide sleeves fiber volume fraction

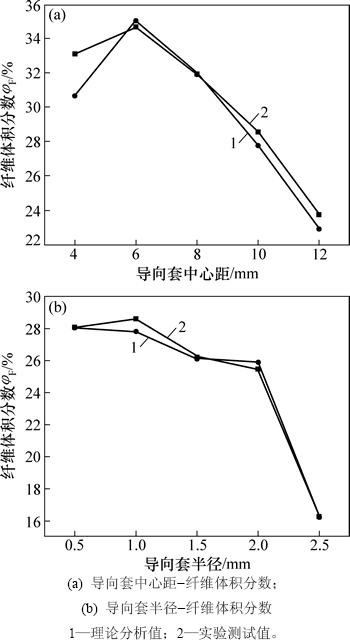
图8  导向套中心距、导向套半径与纤维体积分数的关系

Fig. 8  Relationship among center distance of guide sleeves and radius of guide sleeves and fiber volume fraction

由图9(a)可知：总的纤维体积分数随导向套中心距的增大而减小，表明导向套纤维体积分数变化趋势明显掩盖了纤维规格与导向套中心距匹配出现的最优解；图9(b)中当导向套半径小于2 mm时，总的纤维体积分数随着导向套半径的增大而增大，超过2 mm时，总的纤维体积分数下降，半径为2 mm时是导向套的1个转折点。

在设计复合材料时，需要根据设计要求考虑零部件所要求的是较强的面内力学性能还是Z向性能。若是面内力学性能，则应该选择导向套半径在2 mm以内(包含2 mm)，若更注重Z向强度则选择2 mm及以上，两者兼顾就选择2 mm。复合材料的各向异性和非均匀性，一方面使分析工作复杂化，但在另一方面也给复合材料的设计提供了契机，即人们可以根据不同方向上对材料的不同需求来设计复合材料的结构，以满足工程应用的实际需要，避免过剩和不足的强度和刚度。

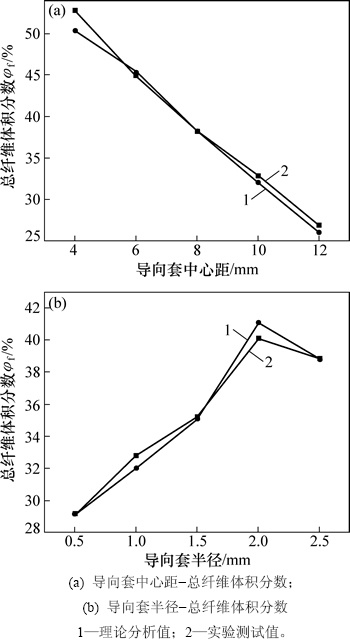
图9  导向套中心距、导向套半径与总纤维体积分数的关系

Fig. 9  Relationship among center distance of guide sleeves and radius of guide sleeves and total fiber volume fraction

5  结论

1) 根据纤维织造路径空间走向的不同，选取基元、边元两类代表性的单元胞体作为细观结构的研究对象，建立了三维织造复合材料的细观模型，并确定了纤维体积分数与细观模型结构参数的关系，其计算值与实际测量值相对一致，相对误差可控制在5%以内。

2) 研究了导向套半径、导向套中心距等结构参数对纤维体积分数的影响，通过合理的结构设计和纤维规格匹配，三维织造复合材料能得到满意的纤维体积分数和弹性模量，并给出了PAN基碳纤维T300三维织造复合材料的导向套半径、导向套中心距等合理工艺参数，以便有效提高其纤维体积分数。

参考文献：

[1] CAO J G, LIU S J, ZHANG J, et al. ASR work roll shifting strategy for schedule free rolling in hot wide strip mills[J]. Journal of Materials Processing Technology, 2011, 211(11): 1768-1775.

[2] CAO J G, XU X Z, ZHANG J, et al. Preset model of bending force for 6-high reversing cold rolling mill based on genetic algorithm[J]. Journal of Central South University (Science & Technology of Mining and Metallurgy), 2001, 18(5): 1487-1492.

[3] 李江鸿, 熊翔, 张红波, 等. 纤维体积分数对碳/碳复合材料力学性能的影响[J]. 中南大学学报(自然科学版), 2005, 36(3): 375-379.

LI Hongjiang, XIONG Xiang, ZHANG Hongbo, et al. Effect of fiber volume fraction on mechanical performances of C/C composites[J]. Journal of Central South University (Science and Technology), 2005, 36(3): 375-379.

[4] 单忠德, 刘丰, 董晓丽, 等. 一种复合材料三维织造成形方法: US8600541B2[P]. 2013-12-03.

SHAN Zhongde, LIU Feng, DONG Xiaoli, et al. A 3D weaving forming method for composites: US8600541B2[P]. 2013-12-03.

[5] SHAN Zhongde, QIN Shaoyan, LIU Qian, et al. Key manufacturing technology & emissions reduction in mechanical equipment industry, international[J]. Journal of Precision Engineering and Manufacturing, 2012, 7(13): 1095-1100.

[6] 单忠德, 陈思思, 刘丰.基于数字化导向模版的复合材料预制件及其制备方法: ZL2012105776892.0[P]. 2013-06-17.

SHAN Zhongde, CHEN Sisi, LIU Feng. The preform of composites and its method of fabrication based on digital guide plate: ZL2012105776892.0[P]. 2013-06-17.

[7] TONG L, MOURITA A P, BANNISTER M K. 3D fiber reinforced polymer composites[M]. UK: Elsevier Science, 153-161.

[8] 马文锁, 赵允岭, 冯伟. 三维编织复合材料理论研究进展[J]. 材料科学与工程学报, 2006, 24(2): 631-636.

MA Wensuo, ZHAO Yunling, FENG Wei. Progressing in the research on 3D braided composites[J]. Journal of Materials Science & Engineering, 2006, 24(2): 631-636.

[9] KO F, BRAIDING K. Engineering materials handbook[M]. Ohio: ASM International, 1987: 519-528.

[10] YANG J M, MA C L, CHOU T W. Fiber inclination model of three-dimensional textile structure composites[J]. Journal of Composite Materials, 1986, 20(5): 472-484.

[11] DU G W, KO F K. Unit cell geometry of 3-D braided structures[J]. Journal of Reinforced Plastics and Composites, 1993, 12(7): 752-768.

[12] 吴德隆, 郝照平. 五向编织结构复合材料的分析模型[J]. 宇航学报, 1993(3): 13-16.

WU Delong, HAO Zhaoping. 5D braided structural composites[J]. Journal of Astronautics, 1993(3): 13-16.

[13] WU D L. Three-cell model and 5D braided structural composites[J]. Composites Science and Technology, 1996, 56(3): 225-233.

[14] 冯伟, 马文锁. 三维编织材料几何结构群论分析[J]. 科学通报, 2005, 50(20): 118-122.

FENG Wei, MA Wensuo. Group theory analysis of 3D braided structural composites[J]. Chinese Science Bulletin 2005, 50(20): 118-122.

[15] 卢子兴, 杨振宇, 刘振国. 三维四向编织复合材料结构模型的几何特性[J]. 北京航空航天大学学报, 2006, 32 (1): 92-96.

LU Zixing, YANG Zhenyu, LIU Zhenguo. Geometrical characteristics of structural model for 3D braided composites[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(1): 92-96.

[16] 杨振宇, 卢子兴, 刘振国. 三维四向编织复合材料力学性能的有限元分析[J]. 复合材料学报, 2005, 55(22): 155-161.

YANG Zhenyu, LU Zixing, LIU Zhenguo. Finite element analysis of the mechanical properties of 3D braided composites[J]. Acta Materiae Compositae Sinica, 2005, 55(22): 155-161.

[17] LOMOV S V, IVANOV D S, VERPOEST I, et al. Meso-FE modeling of textile composites: road map, data flow and algorithms[J]. Composites Science and Technology, 2007, 67(9): 1870-1891.

[18] 杨连贺, 李姜. 三维机织复合材料纱线束截面变形研究[J]. 复合材料学报, 2008, 25(4): 198-203.

YANG Lianhe, LI Jiang. Study on cross-section in three-dimensional woven composites[J]. Acta Materiae Compositae Sinica, 2008, 25(4): 198-203.

[19] 朱元林, 催海涛, 温卫东, 等. 含纤维束截面形状变化的三维编织复合材料细观模型及刚度预报[J]. 复合材料学报, 2012, 29(6): 188-193.

ZHU Yuanlin, CUI Haitao, WEN Weidong, et al. Microstructure model and stiffness prediction of3D braided composites considering yarns’cross-section variation[J]. Acta Materiae Compositae Sinica, 2012, 29(6): 188-193.

[20] 陈林, 刘建军, 邹武. 三维编织复合材料的微结构与力学性能研究进展[J]. 材料导报, 2010, 24(4): 71-72.

CHEN Lin, LIU Jianjun, ZOU Wu. Research development of investigation into microstructure modeling and mechanical properties of three-dimensional braided composites[J]. Materials Review, 2010, 24(4): 71-72.

[21] 刘兆林, 程灿灿. 三维编织复合材料的细观结构与力学性能[J]. 纤维复合材料, 2010, 10(3): 10-12.

LIU Zhaolin, CHENG Cancan. Microstructure and mechanical properties of 3D braided composites[J]. Fiber Composites, 2010, 10(3): 10-12.

[22] 汪星明, 邢誉峰. 三维编织复合材料研究进展[J]. 航空学报, 2010, 31(5): 914-927.

WANG Xingming, XING Yufeng. Developments in research on 3D braided composites[J]. Acta Aeronaautica et Astronautica Sinica, 2010, 31(5): 914-927.

[23] 单忠德, 康怀镕, 臧勇, 等. 三维织造层间增强的纤维棒复合材料细观结构模型及力学性能有限元分析[J]. 复合材料学报, 2015, 32(1): 138-149.

SHAN Zhongde, KANG Huairong, ZANG Yong, et al. Microstructure mode and finite element analysis of mechanical properties of fiber-bar composites reinforced by three dimensional weaving[J]. 2015, 32(1): 138-149.

[24] 乔娟娟. 三维织造导向套与树脂界面结合强度研究[D]. 北京: 机械科学研究总院, 2012: 6-7.

QIAO Juanjuan. Research on interfacial bonding strength between guide-sleeve and resin in 3D weaving[D]. Beijing: China Academy of Machinery Science & Technology, 2012: 6-7.

(编辑  杨幼平)

收稿日期：2015-08-09；修回日期：2015-10-24

基金项目(Foundation item)：国家科技重大专项(2014ZX04001-181)(Project(2014ZX04001-181) supported by the National Science and Technology Major Program of China)

通信作者：单忠德，研究员，博士生导师，从事先进成形技术与装备及复合材料成形技术研究；E-mail：shanzd@cam.com.cn