
Additional transition induced by magnetoelectric interaction in ferroelectromagnet Pb(Fe1/2Nb1/2)O3
YANG Ying(杨 颖)1, HUANG Hong-bo(黄红波)2, SHEN Hong-lie(沈鸿烈)1,
LIU Jun-ming(刘俊明)2, LIU Zhi-guo(刘治国)2
1. College of Materials Science and Technology, Nanjing University of Aeronautics and Astronautics,
Nanjing 210016, China;
2. Nanjing National Laboratory of Microstructures, Nanjing University, Nanjing 210093, China
Received 14 June 2005; accepted 20 October 2005
Abstract: Besides the two phase transitions known in ferroelectromagnets, an additional transition was observed experimentally in Pb(Fe1/2Nb1/2)O3 and the possible mechanism was explored. The magnetic moment shows that anomalous increases when the temperature goes down away from the Néel temperature of 20-30 K. The existence of the hysteresis verifies the weak ferromagnetic property. This additional phase transition is considered to originate from the magnetoelectric coupling between the ferroelectric and antiferromagnetic orders in this compound. From the M?ssbauer parameter analysis, it is confirmed that the hybridization of the O 2p, Fe 3d and Nb 4d electron states makes the realization of magnetoelectric coupling possible.
Key words: Pb(Fe1/2Nb1/2)O3; ferroelectromagnet; magnetoelectric coupling; magnetoelectric interaction; orbital hybridization
I Introduction
Ferroelectromagnets are relatively new class of compounds with ferroelectric (antiferroelectric) and ferromagnetic (antiferromagnetic) orderings coexist- ing in a certain temperature range[1, 2]. The existence of the two ordered subsystems can result in the so-called magnetoelectric effect with interesting device potentials, where the dielectric properties of the ferroelectromagnets may be altered by the onset of the magnetic transition or by the application of a magnetic field, and vice versa.
Pb(Fe1/2Nb1/2)O3 (PFN) has the complex pero- vskite structure and was discovered and synthesized at the end of the 1950s[3]. Its ferroelectric(FE) Curie temperature (TC) is around 383 K and the antiferro- magnetic(AFM) order begins at a Néel temperature of TN=143 K[1, 4-14]. In order to avoid the contradi- cted results caused by the sample inhomogenity, PFN single crystals were grown with high temperature solution growth method and the study of the single crystal samples was concentrated on and powders obtained by grinding them. We have reported a jump in the dielectric constant and loss at the Néel point of PFN, which we assumed to be the result of magnetoelectric interaction[15]. We are interested in the accompanying phenomena and the underlying physics. We noticed in our experiment that besides the assured two phase transitions from paraelectric/ paramagnetic to ferroelectric-paramagnetic and then to ferroelectric-antiferromagnetic, an additional phase transition to a parasitic weak ferromagnetic when the temperature decrease and is away from the Néel point took place. This additional transition was predicted by previous theoretical analysis[1]. The M?ssbauer spectra parameters of 57Fe enriched PFN sample explained the results from the interaction of atomic nucleus and orbital electrons.
2 Experimental
The investigated samples were single crystals grown from high temperature crystal growth method described in previous papers[15, 16]. The crystals yielded were very dark red in color and showed a high degree of luster and pseudo-cube form. The typical size of the crystals was 2-3 mm edge length with the largest ones reaching an edge dimension of 5 mm.
The obtained powders by grinding the grown crystals were characterized by powder X-ray diffraction(XRD) measurement. The space group and the lattice parameters of the grown crystals are in agreement with the former electronic diffraction and neutron diffraction results. The M?ssbauer spectra were measured with a conventional transmission M?ssbauer spectrometer operating in the constant acceleration mode. Absorbers were prepared by finely ground 10% 57Fe enriched PFN crystals, in each case weighed to give optimum signal-to-noise and mixed with carbon to randomize the orientations of the microcrystals. A source of up to 25mCi of 57Co in Palladium matrix was used and the spectrometers were calibrated using α-iron at room temperature and all isomer shifts were quoted relative to the calibration. The M?ssbauer parameters at 20 K were measured with an oxford flow cryostat.
3 Results and discussion
Temperature dependence of magnetic moment (M) of Pb(Fe1/2Nb1/2)O3 was obtained in the vicinity of its Néel temperature and the result is shown in Fig.1. It is noticed that the magnetization first shows an inflexion which corresponds to the reported antiferromagnetic phase transition point at about 143 K and then goes up as temperature(T) continues to decrease at a temperature of 20-30 K below TN. BOKOV et al[3] found this behavior when they published the result of the magnetic property of PFN in 1962. They did not pay attention to the magnetoelectric coupling. They explained that the magnetic moments of some Fe3+ ions in the antiferroelectric regions are not ordered and the system can be considered paramagnetic in the first approximation. In our experiment, we assumed that the increase of magnetic moment at lower temperature may be related to the ferroelectric ordering, since there exists a prediction that the magnetoelectric coupling induces a new transition in ferroelectromagnets[1].
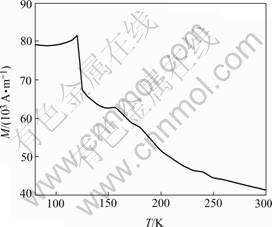
Fig.1 Temperature dependence of magnetic moment under field of 80 A/m
We proved the assumption by measuring the magnetic moment under the applied magnetic field. A magnetic field from 558 A/m to -558 A/m at the temperature of 80 K was applied to the (100)-oriented single crystal PFN sample. Fig.2 shows the hysteresis under the above-mentioned magnetic field. It confirms the existence of weak magnetic property at this temperature.
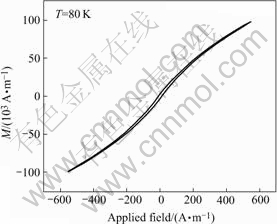
Fig.2 M-H hysteresis measured under magnetic field from -558 A/m to 558 A/m
In order to characterize this additional transition, we measured its specific heat from room temperature down to 4 K. The results are given in Fig.3 and it is found that within our measurement precision, no anomalies are found in the specific heat. There is no evidence showing first order phase transition in this temperature range.
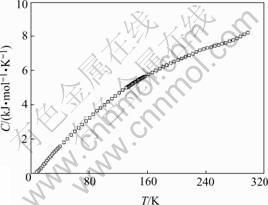
Fig.3 Specific heat of PFN from room temperature to 4 K
As a matter of fact, the perovskite structured materials with transitional metal ions in different oxidation states at their B positions have been found showing several kinds of novel functions in recent years. It was widely investigated both theoretically and experimentally. It has been noticed that the B site cations are of great importance to the physical properties of the materials. Firstly, the distribution of the B site cations in the lattice strongly affects the physical properties of perovskite compound. One B cation interacts with another through oxygen bonds and different neighbors may cause different kinds of interaction with different intensities, which has direct impact on the physical property of the material. The order or disorder of the B cations forms three different types of structure, i.e. random, rock salt and layered structures. Secondly, the different sizes of B cations produce different structure distortions, which are often the source of different behaviors. Furthermore, the subtle differences of the B site ions’ electronic and atomic structures bring forth the significant differences in materials physical properties. Anderson et al[17] obtained a relationship of B site ionic radii difference and their ionic charge difference from both calculation and experiments that if the B site ionic radii difference DR=RB-RB? (RB and RB' are the B cations’ radii) is larger than 0.2 ? and their ionic charge difference DZ=ZB-ZB? (ZB and ZB' are the charges of the B cations) is smaller than 2, the double perovskite B site cations are randomly distributed. According to Shannon radii data[18], Nb5+ with six coordinations has the ionic radius of 0.64 ?; the ionic radius of Fe3+ high spin with six coordinations is 0.645 ?. In PFN, two B site cations are Fe3+ and Nb5+, which have the ionic radii difference of 0.005 ? and their ionic charge difference is 2. Both the ionic radii difference and ionic charge difference lie in the Anderson’s random-distribution range. The B site cations in PFN were assumed to be randomly distributed both from Anderson’s predication. Another calculation method by LIU et al[19] had a different formula on the ordering of double perovskite B site ions distribution also gave the result of random distribution of the B site cations. Former experimental data also confirmed the random distribution of the B site cations[15]. Random distribution of Fe and Nb cations can lead to local fluctuations in composition. Single crystal consists of large number of domains which might have different TC value and resulting broad peaks in the temperature dependent dielectric constant at different frequencies. Fig.4 shows the e—T relations of PFN at different frequencies near its Curie point. We do find there exist broad peaks at each frequency.
Therefore, we admit that the B site cations in PFN are randomly distributed and the magnetic Fe3+ ions are also randomly distributed. Now that the magnetic iron ions (Fe3+) are also randomly distributed, there will be several kinds of indirect exchange interaction. For one Fe3+ ion in a perovskite structure, it lies in the center of an octahedron. The nearest neighbors of any iron ion are six oxygen anions (O2-). The other coordinations connected with the six O2- are possibly either Fe3+ or niobium ions (Nb5+). The O2- ions play a role of transferring the information of the next neighbors. Differences caused by the different next neighbors affect the electric field environment at the nucleus of Fe3+. Thus, there will produce interaction between iron nucleus and the electric field environment, which will cause the electric gradient at the iron nucleus to be nonzero even though the octahedra does not have distinct distortion. The nonzero electric gradient at the nucleus of Fe3+ will no doubt produce the quadrupole splitting hyperfine interaction, which proved by the existence of the doublet of M?ssbauer spectra[15].
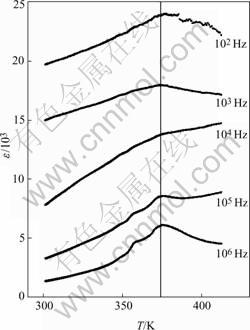
Fig.4 e—T relations of PFN at different frequencies near its Curie point
The existence of iron ions at the B sites provides the opportunity to measure the hyperfine interaction energy by M?ssbauer spectroscopy. Similar attempts have been made earlier[10-12]. We have obtained that below the Néel temperature, the M?ssbauer sextet appears and both the intensity and the position of the sextet increase when temperature decreases[15], which confirms that the magnetic order appears below the Néel temperature. The obtained M?ssbauer parameters are listed in Table 1.
Table 1 M?ssbauer parameters of Pb(Fe1/2Nb1/2)O3 at different temperatures

In Table 1, it can be seen that there is a significant difference between above and below the Néel temperature. At 300K that is above the antiferromagnetic phase transition temperature of 143 K, the quadrupole splitting is 0.42/(10-3m·s-1) and that of 80 K and 20 K are respectively 0.03/(10-3m·s-1) and 0.06/(10-3m·s-1). Pb(Fe1/2Nb1/2)O3 is confirmed to have the rhombohedral space group in the ferroelectric phase below 383 K. The distortion of structure from cubic is very small that the rhombohedral has the angel of 89.92°[3, 20]. The powder XRD result of crystal at different temperatures indicated that there is no distinct peak shift in the experimental temperature range[14]. Since no distinct structure differences below and above the Néel temperature are observed, the quadrupole splitting which comes from the interaction of nuclear moment with an asymmetric electronic charge distribution will benefit little from the structure change.
Because there is little crystal structure change in Pb(Fe1/2Nb1/2)O3 between both above and below its Néel temperature, the significant quadrupole splitting change may come from the influence of magnetic order to the orbital hybridization. At room temperature, PFN is in its paramagnetic phase and so the B site cations are all completely magnetic disordered. Therefore, the electrons in the valence band are strongly scattered. The charge transportation ability along Fe-O-Nb bond is restricted. Below the Néel temperature, the onset of the antiferromagnetic ordering brings forth the polarization of the electrons in the valence band. The spins of five 3d electrons of Fe3+ have the opposite direction with the spin of four 4d Nb5+ ions. Their hybridization through the 2p orbital of O2- is strengthened. In this way, the number of 3d electrons of Fe3+ increases and this leads to the isomer shift value as shown in Table 1. Actually, From Table 1, it can be seen that the isomer shift value of Pb(Fe1/2Nb1/2)O3 at 80 K and 20 K are 0.50, which is larger than the typical isomer shift value of the trivalence high spin state iron ions. It indicates that the valence of Fe ion is smaller than trivalence. This change of valence coming from the additional electrons appears on the 3d orbital of Fe ions. In this case, there are 5+δ electrons on the 3d orbital of Fe. The additional δ comes from the hybridization with Nb ions. At the same time, the eg orbital of iron ions in the octahedral crystal field receives extra electrons from the hybridization, which decrease the quadrupole splitting significantly.
The hybridization of the Nb 4d electron with O 2p has been confirmed in many cases. For example, DUAN et al[21] calculated the total and partial densities of states of KNbO3 and found that the bottom of the conduction band is mostly derived from Nb 4d electron states, while the O 2p electrons dominate the top of the valence band, a mixture of Nb 4d and O 2p electron states in the valence band (-5 eV to 0 eV) is also significant. They considered that the nonlinear optical behavior of KNbO3 comes from the hybridization of the O 2p and Nb 4d electron states. UHM et al[22] also found the strong hybridization between Fe 3d and O 2p orbitals in perovskite R1/3Sr2/3FeO3 (R=Pr, Sm, and Nd), which also have Fe ions on the B site of perovskite structure.
From the above discussions and examples, we considered that there exist hybridization among the Fe 3d orbital, O 2p orbital and Nb 4d orbital in Pb(Fe1/2Nb1/2)O3. It is the electronic orbital hybridization that creates possibility for the existence of magnetic and ferroelectric coupling and the induced additional transition. If there is no hybridization, the electrons in both Fe3+ and Nb5+ are localized and the indirect exchange between Fe3+-O2--Fe3+ is also randomly distributed, and the exchange interaction on the conductive band cannot carry through.
4 Conclusions
An additional transition in Pb(Fe1/2Nb1/2)O3 (PFN) single crystals grown by high temperature solution method has been found. The M-T curve shows a transition to weak magnetic property below the Néel temperature. The M-H hysteresis confirms the existence of the weak magnetic property. This additional transition is considered to originate from the magnetoelectric interaction between the ferroelectric and antiferromagnetic orders in this compound. The hybridization of the O 2p, Fe 3d and Nb 4d electron states serves as the platform for the existence of magnetoelectric coupling and the additional transition to weak ferromagnetic property.
References
[1] SMOLENSKII G A. Ferroelectromagnets[J]. Soviet Physics: Solid State, 1982, 29: 475-493.
[2] SCHMID H. Introduction to the processing of MEIPIC-2[J]. Ferroelectrics, 1994, 1: 161-164.
[3] BOKOV B A, MYLNIKOVAL I E, SMOLENSKII G A. Ferroelectric antiferromagnetics[J]. Sov Phys JETP, 1962, 15: 447-450.
[4] ASTROV D N, AL’SHIN B I, ZORIN R V. Spontaneous magnetoelectric effect[J]. Sov Phys JETP, 1969, 28: 1123-116.
[5] HOWES B, PELLIZZONE M, FISHER P. Characterization on some magnetic and magnetoelectric properties of ferroelectric Pb(Fe1/2Nb1/2)O3[J]. Ferroelectrics, 1984, 54: 217-320.
[6] WATANABLE T, KOHN K. Magnetoelectric effect and low temperature transition of Pb(Fe0.5Nb0.5)O3 single crystals[J]. Phase Transitions, 1989, 15: 57-68.
[7] RANDALL C A, BAHALLA A S. Nanostructural-property relations in complex lead perovskites[J]. Jpn J Appl Phys Part Ⅰ, 1990, 29: 327-330.
[8] YOKOSUKA M. Electrical and electromechanical properties of hot-pressed Pb(Fe1/2Nb1/2)O3 ferroelectric ceramics[J]. Jpn J Appl Phys Part Ⅰ, 1993, 32: 1142-1145.
[9] BONNY V, BONIN M, SCIAU P, SCHENK K J, CHAPUIS G. Phase transitions in disordered lead iron niobate: X-ray and synchrotron radiation diffraction experiments[J]. Solid State Commun, 1997, 102: 347-352.
[10] ANANTA S, THOMAS N W. A modified two-stage mixed oxide synthetic route to lead magnesium niobate and lead iron niobate[J]. J Euro Ceramic Soc, 1999, 19: 155-163.
[11] ANANTA S, THOMAS N W. Relationships between sintering conditions, microstructure and dielectric properties of lead iron niobate[J]. J Euro Ceramic Soc, 1999, 19: 1873-1881.
[12] ANANTA S, THOMAS N W. Fabrication of PMN and PFN ceramics by a two-stage sintering technique[J]. J Euro Ceramic Soc, 1999, 19: 2917-2930.
[13] BRUNSKILL I H, BOUTELLIER R, DEPMEIRER W, SCHMID H. High-temperature solution growth of Pb(Fe0.5Nb0.5)O3 and Pb(Mn0.5Nb0.5)O3 crystals[J]. J Cryst Growth, 1982, 56: 541-546.
[14] BRUNSKILL I H, TISSOT P, SCHMID H. Determination of the phase diagrams, PbO-Pb(Fe1/2Nb1/2)O3 and Pb-Pb(Mn1/2Nb1/2)O3 [J]. Thermochimica Acta, 1981, 49: 351-355.
[15] YANG Y, LIU J M, HUANG H B, ZOU W Q, BAO P, LIU Z G. Magnetoelectric coupling in ferroelectromagnet Pb(Fe1/2Nb1/2)O3 single crystals[J]. Phys Rev B, 2004, 70: 132101.
[16] YANG Y, HUANG H B, LIU J M, LIU Z G. Mossbauer studies on high temperature solution grown Pb(Fe1/2Nb1/2)O3 single crystals[J]. Ferroelectrics, 2002, 280: 75-82.
[17] ANDERSON M T, GREENWOOD K B, TAYLOR G A. B-cation arrangements in double perovskites[J]. Prog Solid State Chem, 1993, 22: 197-223.
[18] SHANNON R D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides[J]. Acta Crystallographica, 1976, A32: 751-767.
[19] LIU R, XUAN Y, JIA Y Q. A simple method for judging order to disorder in A(BIBI’)O3 perovskite compounds[J]. J Solid State Chem, 1997, 134: 420-422.
[20] IVANOV S A, TELLGREN R, RUNDLOF H, THOMAS N W, ANANTA S. Investigation of the structure of the relaxor ferroelectric Pb(Fe1/2Nb1/2)O3 by neutron powder diffraction[J]. J Phys: Condens Matter, 2000, 12: 2393-2397.
[21] DUAN C G, MEI W N, LIU J J, HARDY J R. First-principle study on the optical properties of KNBO3[J]. J Phys: Condens Matter, 2001, 13: 8189-8192.
[22] UHM Y R, LEE S W, PARK K T, TOMIOKA Y, TOKURA Y, KIM C S. Charge ordering and mossbauer studies of single crystal R1/3Sr2/3FeO3(R=Pr, Sm, and Nb)[J]. J Appl Phys, 2000, 87: 4873-4876.
Foundation item: Projects(50572038; 10374048) supported by the National Natural Science Foundation of China
Corresponding author: YANG Ying; Tel: +86-25-84891937; E-mail: yingyang@nuaa.edu.cn
(Edited by LI Xiang-qun)