J. Cent. South Univ. (2019) 26: 3328-3337

DOI: https://doi.org/10.1007/s11771-019-4256-7

Parameters estimate of recurrent quantum stochastic filter for time variant frequency periodic signals

ZHOU Li-chun(周丽春), JIN Fu-jiang(金福江), WU Hao-han(吴浩瀚), WANG Bo(王波)

College of Mechanical Engineering and Automation, Huaqiao University, Xiamen 361021, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: Designing optimal time and spatial difference step size is the key technology for quantum-random filtering (QSF) to realize time-varying frequency periodic signal filtering. In this paper, it was proposed to use the short-time Fourier transform (STFT) to dynamically estimate the signal to noise ratio (SNR) and relative frequency of the input time-varying frequency periodic signal. Then the model of time and space difference step size and signal to noise ratio (SNR) and relative frequency of quantum random filter is established by least square method. Finally, the parameters of the quantum filter can be determined step by step by analyzing the characteristics of the actual signal. The simulation results of single-frequency signal and frequency time-varying signal show that the proposed method can quickly and accurately design the optimal filter parameters based on the characteristics of the input signal, and achieve significant filtering effects.

Key words: quantum stochastic filter (QSF); parameters estimation; least square (LS); short-time Fourier transform (STFT)

Cite this article as: ZHOU Li-chun, JIN Fu-jiang, WU Hao-han, WANG Bo. Parameters estimate of recurrent quantum stochastic filter for time variant frequency periodic signals [J]. Journal of Central South University, 2019, 26(12): 3328-3337. DOI: https://doi.org/10.1007/s11771-019-4256-7.

1 Introduction

The quantum stochastic filter (QSF) is a new stochastic filtering algorithm, which has been used in many signal processing fields [1-5]. QSF does not need any prior knowledge of the observed signal [6-8]. The introduction of Schrodinger wave formula leads the QSF to a non-linear stochastic system [9, 10]. As for the QSF, the values of the related parameters were trained traditionally by some intelligent algorithms. The genetic algorithm (GA) based on the concept of univariate marginal distribution algorithm (UMDA) was used to select near-optimal parameters in Refs. [1, 11]. GANDHI et al [5] used a two-step inner-outer 5-fold cross- validation and a particle swarm optimization (PSO) to select the parameters. However, almost all the reported algorithms are the intelligent optimization algorithms. Up to now, little attention has been concentrated on the simplification of parameters training for the QSF.

Generally speaking, the intelligent optimization algorithms are very time-consuming and sophisticated [12]. In addition, the optimized parameters cannot be updated dynamically. What is worse, we can not use any intelligent optimization algorithms, since we cannot know the general shape of the actual signal previously in many cases [12]. Thus, it is necessary to find a new way to achieve QFS in practice which is time saving and does not need the prior knowledge of the observation.

In this paper, two functions for two parameters for single frequency input signals are established. The first one is the function time-interval of Schrodinger wave formula relying on relative frequency, and the second one is the function iterate times relying on the relative frequency and the raw signal to noise rate (SNR, R). Then, the scopes of such two functions are extended from the case of single-frequency input signal to the case of general input signal by estimating the frequency and SNR dynamically through the short-time Fourier transform (STFT). It is found that the other parameters could be fixed for all actual signals in a special architecture of QSF by analyzing frequency characteristics of the actual signal. Besides, it is worth pointing out that the architecture of QSF used in this paper, in which a new method is proposed, is an improvement of QSF in Ref. [4].

The remainder of the paper is organized into seven sections. In Section 2, a brief introduction of QSF is presented. Section 3 shows the reason why many parts of the parameters can be fixed. Section 4 gives the function formula between relative frequency and interval time of Schrodinger wave formula, and the function formula between relative frequency iterations and raw SNR for single- frequency input signal. In Section 5, the scopes of the above two formulas are extended by using the STFT. Section 6 discusses the effect of the improper non-system parameters. In Section 7, the simulation results are presented. Section 8 is a conclusion of the full paper.

2 Parameters of quantum stochastic filter

The schematic of quantum stochastic filter is presented in Figure 1. The initial state function ψ_i(x, t) is constructed by using output signal y(t) and noise ε(x, t). The signal state function influenced by time variant noise is ψ_o(x, t), and it can be got by using Schrodinger wave formula (SWF). Probability density function(PDF) and mean of y(t) are also computed, and then filtering is completed. The function of potential field is the key of SWF. In this paper, the function of potential is presented by using neural network and its model is constructed by using recurrent quantum neural network (RQNN) [1-5]. The detailed schematic diagram of the RQNN used in this paper is presented in Figure 2.

As shown in Figure 2, y(t) is an observed signal embedded with unknown noise whose statistical mean is zero. In addition, f(x, t) is a variance variable Gaussian kernel function, which is modulated by y(t) and e(t), and is expressed as:

         (1)

From Eq. (1), we know that the center of the Kernel function moves with the changing of the observed signal. This is very important to track the actual signal embedded in the observed signal. At the same time, the variance of f(x, t) would change with e(t), which could solve the contradiction between the stability and accuracy of the filter. Thus, the neural network is used to adjust the shape of the potential field as follows:

            (2)

If f(x, t) is the input of the neural network and 1+e²(t) is the output, then a variant of the Hebbian learning algorithm [10-13] can be used to update dynamically the weight of the neural network w(x, t), which is formulated as Eq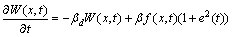. (3):

       (3)

where

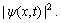
Figure 1 Schematic diagram of QSF

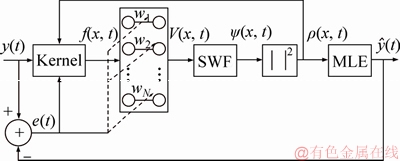
Figure 2 RQNN’s framework of function of potential field

The process of varying ψ(x, t) is described by SWF [5] as follows:

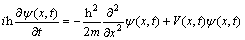      (4)

To numerically solve the SWF in Eq. (4), the following finite difference time domain (FDTD) method is exploited:

     (5)

where n=1, 2, …, and j=1, 2, …, M. In addition, is Planck’s constant divided by 2π; i is the imaginary unit m is the mass of the imaginary particle. For presentation convenience, we use ψ_nj to represent ψ(n△t, j△x). In Figure 2, the receptive fields of M neurons span the entire distance along the x-axis. Thus, the x-axis is divided into M mesh points, and each point represents a neuron lattice. Rewriting Eq. (5) yields:

                      (6)

where .

By defining the following Hamiltonian

Equation (6) is reformulated as below:

                              (7)

where

Since the primary QND cannot track the high frequency actual signal, a new parameter γ is added. Such a parameter represents the number of iterative steps that are required for the response of the SWF to reach a steady state to an instant sample of the external stimulus y(n). Thus, Eq. (7) can be modified as follows:

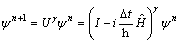              (8)

In practice, we can properly enlarge △t to decrease γ to reduce the computational complexity. This means that △t is another new parameter irrelevant with the sampling interval dt, and △x is the spatial separation between adjacent neural lattices. Thus, eight parameters, i.e., m, ζ, β, β_d, a₁, a₂, △t, γ, are needed to be fixed for an actual signal, which is time-consuming, inconvenient and even impossible with the traditional methods. Due to the in-depth researches, in a fixed architecture of RQNN, m, ζ, β, β_d, a₁, a₂, can be fixed for any input signal, which is discussed in the ensuing section.

3 System parameters of a specific RQNN

The essence of stochastic filtering is the computation of a time-varying probability density function on the state of the observed system. In RQNN, the state is assumed to be something in the mind of the observer and the conversion formula of the state is assumed to be the SWE. All we need to do is to translate the observe signal y(t) into the potential function of the SWE to control the evolution of the state ψ(x, t).

Specifically, the parameters in the cognitive process represent the cognitive ability or sensitivity of the intelligent system. Note that the cognitive ability of a special intelligent system should be fixed. Thus, the parameters m, ζ, β, β_d, a₁, a₂ can be assumed fixed for a simulated intelligent system. Since m is the mass of the imaginary particle in the mind of the observer, it should also be fixed. Therefore, the parameters m, ζ, β, β_d, a₁, a₂ and m are defined as the system parameters. When the architecture of the RQNN was fixed, the values of such system parameters could be determined by the genetic algorithm (GA). In this paper, these system parameters are set as follows:

Now we just need to find the values of the other parameters. △t and γ are defined as non- system parameters for a given different actual signal. The choices of such two non-system parameters are discussed in the ensuing section.

Figure 3 Function formula between interval and relative frequency N

4 Establishing model of non-system parameters for single-frequency input signal

Define relative frequency N as Eq.(9):

                               (9)

In this paper, both of △t and γ are used to improve/enhance the ability of tracking the actual signal. However, excessive △t may reduce the accuracy of the filter, and excessive γ may lead to the non-smoothness of the output signal. To show the filtering performance of the RQNN, the following root mean square error (RMSE) is used.

Assuming that the system parameters are fixed as described in section 3, both the theoretical analysis and experimental simulations show that △t and γ are complement each other but not interchangeable. At the same time, we do not want to use excessive γ, as it means time-consuming. Then the value of △t is determined via the following steps: 1) use GA to select an optimal △t, whose goal is to minimize the RMSE within experiential range; 2) traverse to find the optimal γ; 3) back to the first step until the RMSE does not change too much, then record the △t as the optimal △t.

By using least squares (LS) method, the relationship between △t and N is fitted as:

                       (10)

Now the LS method [14-18] is reused to establish a function formula between γ and N. Through the experiments, it is found that the relationship between γ and N can be an exponential relationship. Note that the parameters of such an exponential function are the functions relying on signal to noise ratio. Thus, the arguments of γ should be based on N and SNR. By using the LS method, the functions relying on SNR are fitted. In view of γ that is an integer, the formula of γ is presented as Eq. (11):

                          (11)

where A, B and C are defined respectively as:

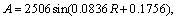
Evidently, Eq. (11) shows that γ has an exponential relationship with relative frequency N. More intuitive results can be seen from Figure 4. As shown in Figure 4, less N corresponds to greater γ with the same R, and less R means greater with the same N.

Figure 4 Function formula between γ and relative frequency N

5 Establishing model of non-system parameters for general signal

As for Eqs. (10) and (11), they are obtained with the fixed frequency as well as the fixed SNR. Note that the general signal is band pass signal, but its frequency generally does not change too much within △T, as illustrated in Figure 5. Therefore, the average frequency before the △T period can be estimated with respect to t. Then, the modified average frequency is regarded as the frequency of actual signal in moment t. Meanwhile, the average SNR estimated in the same period is also regarded as the input SNR in moment t. The values of γ and t can thus be updated dynamically.

Figure 5 Introduced schematic diagram of window function

To lay a basis for further discussion, three assumptions are given as follows:

1) The frequency of the actual signal does not change too much within △T.

2) The SNR of the raw signal does not change too much within △T.

3) The filtered signal of the RQNN is very accuracy.

Suppose that y(t) is the input (raw) signal and is the estimated signal in moment t. Then, the corresponding Fourier transforms within △T previous period with respect to t are formulated as:

                 (12)

where subscript t signifies the deadline.

5.1 Dynamically estimation of SNR

The power spectral densities of the input and output signal are expressed respectively as Eq. (13):

                      (13)

                      (14)

Thus, the corresponding input power and output power are expressed as:

                           (15)

Hence, the SNR can be estimated as Eq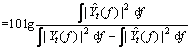.(16):

         (16)

Using Parseval theory, it could also be reformulated as:

         (17)

5.2 Estimate of center frequency within △T

As for Eq. (12), it may introduce additional high frequency component caused by direct interception. Thus, by introducing a window function the modified form of Eq. (12) is presented as follows:

            (18)

Note that there are a number of window functions that can be used. For example, the Hanning one is given as below:

 (19)

The interception process is illustrated in Figure 5.

The modified Fourier transform has changed the spectrum, but the center frequency does not change at all. Hence, the modified Fourier transform can be used to estimate the center frequency of the actual signal during [t-△T, t]. As the input (observed) signal is embedded with white noise signal, the power spectral density (PSD) of the raw signal should be considered as follows.

As the noise is supposed to be white noise and the frequency of the actual signal does not change too much during [t-△T, t], the PSD of the observed signal can thus be approximatively indicated in Figure 6. Assume that is the unilateral PSD of y(t) whose bilateral PSD isAll we need to do is to estimate the center frequency f₀. Suppose

                (20)

where L_p should neither be too great nor too small. In this paper, it is set as:

                    (21)

The average frequency can be regarded as the center frequency. If we insure then the pp_t(f) can be regarded as a probability density function of the frequency f. Thus, the center frequency could be estimated as:

 (22)

where F is a finite quantity but great enough to surpass any possible frequency of the actual signal. In this case, it should be insured that On the one hand, the introduction of F can reduce the complicity of numerical calculation. On the other hand, it can be used to stabilize both the estimated frequency and the SWE, which will be discussed in Subsection 5.4. Besides, the variance of f is used to evaluate the accuracy of △T, and the maximum likelihood estimation (MLE) is used to estimate the center frequency for colored noise.

Figure 6 Schematic diagram of PSD of observed signal

Now the Instantaneous frequency f_t(t) can be estimated byas Eq. (23):

           (23)

The reason why we use Eq. (19) to estimate f_t(t) will be analyzed in Section 6.

5.3 Numerical form of above two estimates

Based on Eq. (16), the estimate of R(t) can be expressed numerically as

      (24)

where t=i·dt, and i=1, 2, …. To insure the finite and accurate of the SNR estimate, Eq. (24) is modified as

  (25)

where

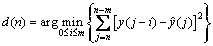         (26)

Here d(n) is the estimated delay in moment n, m is the expected delay bound in Eq. (26) and m=△T/dt.

Now let us consider the numerical form of center estimate. First, the continuous signal is sampled as Eq. (27):

             (27)

Second, its PSD is determined via the discrete Fourier transform (DFT) as Eq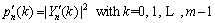. (28):

         (28)

where

with 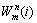being defined as Eq. (29):

(29)

Third, the bilateral power spectrum density is determined as Eq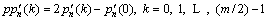. (30):

 (30)

Suppose F_s=1/dt≥F, then the range of digital frequency △f is represented as Eq. (31):

L=F/△f                    (31)

In addition, suppose Eq. (32):

                   (32)

where

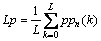                                                                    (33)

Then the estimated center frequency can be formulated as Eq. (34):

                   (34)

where

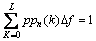                         (35)

Now the instantaneous frequency f_n(n) is estimated as Eq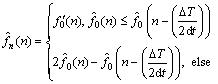. (36):

        (36)

5.4 Stability condition of Schrodinger wave formula

If the finite-difference method is used to solve the SWE, the stability condition must be insured. The stability condition is formulated as Eq. (37) [19, 20]:

                   (37)

Thus, we have

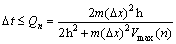              (38)

where V_max(n) is the maximum of the potential field in moment n. By considering Eqs. (9) and (10), the relative frequency in moment n must obey

                (39)

which yields

                    (40)

Note that, via Eqs. (39) and (40), we have 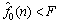andThus, the following result is obtained:

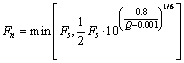             (41)

where F_n represents F in moment n. Therefore, the stability of SWE in moment (n+1) can be insured for any estimated △t if F obeys Eq. (41).

6 Steps of filtering and simulation

According to Eqs. (10), (11), (26) and (36), m, ζ, β, β_d, a₁, a₂ parameters of RQNN were estimated, the function of potential field is determined, and PDF of time-varying signal and mean is computed. The specific steps of QSF as follows:

1) According to Eqs. (10), (11), (26) and (36), estimate parameters △t, γ and of RQNN;

2) According to Eq. (2), (3), (5), construct function of potential field using RQNN;

3) According to Eq. (8), get the state function of signal by influenced time variant noise as ψ_o(x, t) and PDF;

4) Compute mean of time-varying signal using PDF, and complete filtering to get raw of signaland

5) Stop computing while the root mean square errors of and y(t) are less than △.

7 Simulation results

In this section, a sinusoid signal is filtered by two methods to show the effectiveness of Eqs. (10), (11). Then, another sinusoid signal whose time- varying frequency is filtered to show the ability of frequency estimate of approach in this paper.

In this example, the raw signal is given as Eq. (42):

   (42)

where D=0.1 s and n(t) is the nonstationary noise. In addition, the frequency is a function relying on t, which can be determined as Eq. (43):

   (43)

Estimate γ and △t dynamically by Eqs. (10), (11), (25) and (36). The corresponding filtered result is shown in Figure 7. The estimated parameters are as follows:

As seen from Eq. (36) and Figure 7, the SNR and frequency are both time-variant. In addition, the filtering result is always very well for the dynamical estimation of the frequency and the SNR from Eqs. (10) and (11). The estimated frequency is shown in Figure 8 and the estimated SNR is shown in Figure 9.

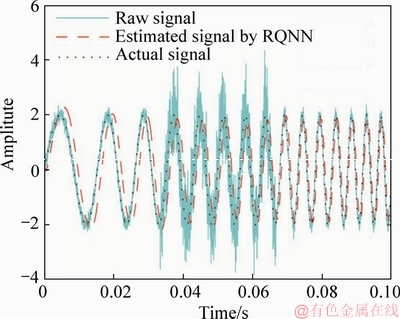
Figure 7 Filtered result of RQNN for frequency modulation signal

Figure 8 Estimated frequency change with time

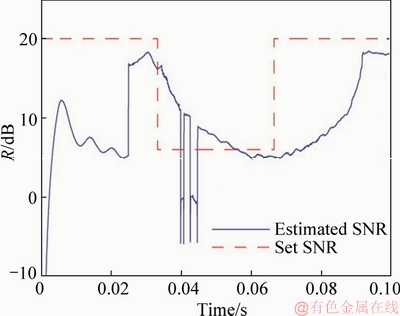
Figure 9 Estimated SNR

As seen from Figure 8, the reason why the estimated frequency in [0 0.025] s is const is that the data width for the STFT is about 0.025 s. This also means that the beginning 0.025 s is initialization period.

As seen from Figure 9, it is very interesting that the estimated SNR is almost much lower than the preset one. In fact, this is very important to make up filtering error though enhancing the track ability of the RQNN, which has been detailed in Section 6.

Now we consider the same raw signal filter by the fixed parameters to reflect the advantage of dynamical parameter estimate. In this case, we just consider the effect of the a proper frequency for the SNR that has little effect by Eq. (11).

Assuming f≡50 Hz, the corresponding filtering result is shown in Figure 10. As seen from Figure 10, the filter works very well in the beginning, but it diverges later. This is because the actual frequency is greater than 50 Hz as time goes on. Note that the frequency error causes the divergence, which has been detailed in Section 4.

Figure 10 f≡50 Hz filtering result

Assuming f≡250 Hz, the corresponding filtering result is shown in Figure 11. As seen from Figure 11, it is same as that the filtering result is very well when f≡250 Hz which is the max actual frequency. However, the smoothness of the filtering result is very bad, and over frequency.

Figure 11 f≡250 Hz filtering result

From Figures 7, 10 and 11 we can have the conclusion that the approach presented real effectiveness for the frequency modulation signal, which also means the time-consuming for the great γ by Eq. (11).

8 Conclusions

A reasonable assumption for the functional formula was proposed time interval of SWE and relative frequency, which is defined as the dividing sampling frequency by cutoff frequency of the actual signal. Time interval, relative frequency and model coefficients could be fixed by using algorithm. The efficiency of SWF is obviously improved by using parameters model compared to intelligent optimization algorithms.

A kind periodic signal of time-varying frequency and containing unknown noise can be recurrent by using QSF, which illustrates that designed RQNN parameter is reasonable.

Acknowledgment

The authors would like to thank Prof. L BEHERA for guiding this paper. Besides, the authors would also like to thank the editors and anonymous reviewers for their time and effort spent handling this paper, as well as for providing constructive comments to further improve the presentation and quality of this paper.

References

[1] MARQUEZ F P G, NIETO M R M. Recurrent neural network and genetic algorithm approaches for a dual route optimization problem: A real case study [C]// Lecture Notes in Electrical Engineering. London: Springer, 2012: 23-37. DOI:10.1007/978-1-4471-4600-1_2.

[2] GANDHI V, ARORA V, BEHERA L, PRASAD G, COYLE D H, MCGINNITY T M. A recurrent quantum neural network model enhances the EEG signal for an improved brain-computer interface [C]// IET Seminar on Assisted Living. Piscataway, NJ, USA: IEEE, 2011: 12.

[3] REBENTROST P, BROMLEY T R, WEEDBROOK C, LLOYD S. Quantum hopfield neural network [J]. Physical Review A, 2018, 98(4): 042308. DOI: 10.1103/PhysRevA. 98.042308.

[4] GANDHI V S, MCGINNITY T M. Quantum neural network based surface EMG signal filtering for control of robotic hand [C]// The 2013 International Joint Conference on Neural Networks (IJCNN). New York, USA: IEEE, 2013: 1-7.

[5] GANDHI V, PRASAD G, COYLE D, BEHERA L, MCGINNITY T M. Quantum neural network-based EEG filtering for a brain-computer interface [J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(2): 278-288. DOI: 10.1109/TNNLS.2013.2274436.

[6] FERNANDEZ E A, WILLSHAW P, PERAZZO C A, PRESEDO R J, BARRO S. Detection of abnormality in the electrocardiogram without prior knowledge by using the quantisation error of a self-organising map, tested on the European ischaemia database [J]. Medical & Biological Engineering & Computing, 2001, 39(3): 330-337. DOI: 10.1007/BF02345228.

[7] LUITEL B, VENAYAGAMOORTHY G K. Quantum inspired PSO for the optimization of simultaneous recurrent neural networks as MIMO learning systems [J]. Neural Networks, 2010, 23(5): 583-586. DOI: 10.1016/j.neunet. 2009.12.009.

[8] HYOUNG-UK H, KIM J K. An evolutionary genetic neural networks for problems without prior knowledge [C]// 2014 10th International Conference on Natural Computation (ICNC). New York, USA: IEEE, 2014: 1-6.

[9] KATZ G E, REGGIA J A. Using directional fibers to locate fixed points of recurrent neural networks [J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(8): 3636-3646. DOI: 10.1109/TNNLS.2017. 2733544.

[10] MU Yu-qiang, SHENG An-dong, GUO Zhi. Evolutionary diagonal recurrent neural network for nonlinear dynamic system identification [C]// 2008 IEEE International Conference on Networking, Sensing and Control. New York, USA: IEEE, 2008: 837-841.

[11] KUMAGAI T, WADA M, HASHIMOTO R, UTSUGI A. Dynamical control by recurrent neural networks through genetic algorithms [J]. International Journal of Adaptive Control and Signal Processing, 2015, 13(4): 261-271. DOI: 10.1002/(SICI)1099-1115(199906)13:4<261::AID-ACS546>3.0.CO;2-N.

[12] LI Zhan-ying, WANG Ke-jun, TANG Mo. Optimization of learning algorithms for chaotic diagonal recurrent neural networks [C]// 2010 International Conference on Intelligent Control and Information Processing. New York, USA: IEEE, 2010: 244-247.

[13] CHEN Sheng-tan. Signal and systems [M]. Xi’an: Xi’an University of Electronic Science and Technology Press, 2001. (in Chinese)

[14] GAO Xi-quan, DING Yu-mei. Digital signal processing [M]. Xi’an: Xi’an University of Electronic Science and Technology Press, 2016. (in Chinese)

[15] WU Hao-han, JIN Fu-jiang, LAI Lian-you, WANG Liang. A stochastic filtering algorithm using Schrodinger equation [J]. Acta Automatica Sinica, 2014, 40(10): 2370-2376. DOI: 10.1016/S1874-1029(14)60366-9.

[16] LAI Lian-you, JIN Fu-jiang, WU Hao-han. Quantum random filter denoising method for speech signal [J]. Information and Control, 2015, 44(5): 598-603. DOI: 10.13976/j.cnki. xk.2015.0598. (in Chinese)

[17] CHEN Guang, REN Zhi-liang, SUN Hai-zhu. Least-squares curve fitting and Matlab realize [J]. Ordnance Industry Automation, 2005, 24(3): 107-108. (in Chinese)

[18] LV Xi-ming, LI Ming-yuan. Least-squares curve-fitting in MATLAB [J]. Journal of Inner Mongolia University for Nationalities (Natural Sciences), 2009, 24(2): 125-127. DOI: 10.14045/j.cnki.15-1220.2009. 02.035. (in Chinese)

[19] KUANG Xiao-jing, WU Xian-liang, HUANG Zhi-xiang, WANG Dao-ping. Solving time-dependent Schrodinger formula based on FDTD method [C]// Proc National Conference on Microwave and Millimeter Wave. Xi’an, China: Publishing House of Electronics Industry, 2009: 990-993. (in Chinese)

[20] GIORDANO N J, NAKANISHI H. Computational physics [M]. 2nd ed. Beijing, China: Tsinghua University Press, 2007.

(Edited by ZHENG Yu-tong)

中文导读

时变频率周期信号的递归量子随机滤波器参数估计

摘要：设计最优时间和空间差分步长是量子随机滤波(QSF)实现时变频率周期信号滤波的关键技术。本文提出用短时傅立叶变换(STFT)动态地估计输入时变频率周期信号的信噪比(SNR)和相对频率，用最小二乘法建立量子随机滤波器时间和空间差分步长与信噪比(SNR)和相对频率的模型，通过分析实际信号的特征可以逐步确定量子滤波器的参数。针对单频信号情况和频率时变信号的仿真实验结果表明，该方法能够根据输入信号的特征，快速、准确设计出滤波器最优参数，取得显著的滤波效果。

关键词：量子随机滤波器；参数估计；最小二乘；短时傅立叶变换

Foundation item: Projects(2017H0022, 2016H6015) supported by Fujian Science and Technology Key Project, China

Received date: 2018-12-10; Accepted date: 2019-10-22

Corresponding author: ZHOU Li-chun, PhD, Lecturer; Tel: +86-592-6162364; E-mail: 13905958730@163.com; ORCID: 0000-0002- 6561-7656