J. Cent. South Univ. (2019) 26: 2878-2890

DOI: https://doi.org/10.1007/s11771-019-4221-5

An improved joint method for onset picking of acoustic emission signals with noise

ZHOU Zi-long(周子龙)¹, CHENG Rui-shan(程瑞山)¹, CHEN Lian-jun(陈连军)²,ZHOU Jing(周静)¹, CAI Xin(蔡鑫)¹

1. Faculty of Mining Engineering, School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. State Key Laboratory of Mining Disaster Prevention and Control, Shandong University of Science and Technology, Qingdao 266590, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: The onset times of acoustic signals with spikes, heavy bodies and unclear takeoffs are difficult to be picked accurately by the automatic method at present. To deal with this problem, an improved joint method based on the discrete wavelet transform (DWT), modified energy ratio (MER) and Akaike information criterion (AIC) pickers, has been proposed in this study. First, the DWT is used to decompose the signal into various components. Then, the joint application of MER and AIC pickers is carried out to pick the initial onset times of all selected components, where the minimum AIC position ahead of MER onset time is regarded as the initial onset time. Last, the average for initial onset times of all selected components is calculated as the final onset time of this signal. This improved joint method is tested and validated by the acoustic signals with different signal to noise ratios (SNRs) and waveforms. The results show that the improved joint method is not affected by the variations of SNR, and the onset times picked by this method are always accurate in different SNRs. Moreover, the onset times of all acoustic signals with spikes, heavy bodies and unclear takeoffs can be accurately picked by the improved joint method. Compared to some other methods including MER, AIC, DWT-MER and DWT-AIC, the improved joint method has better SNR stabilities and waveform adaptabilities.

Key words: Akaike information criterion (AIC); modified energy ratio (MER); discrete wavelet transform (DWT); acoustic signals with noise

Cite this article as: ZHOU Zi-long, CHENG Rui-shan, CHEN Lian-jun, ZHOU Jing, CAI Xin. An improved joint method for onset picking of acoustic emission signals with noise [J]. Journal of Central South University, 2019, 26(10): 2878-2890. DOI: https://doi.org/10.1007/s11771-019-4221-5.

1 Introduction

Accurate identifications for onset times of earthquake, micro-seismic and acoustic emission (AE) signals are of great significance for data processing, event identification, location estimation [1-13]. However, spikes, heavy bodies and unclear onset times are often encountered in the signal records. The spikes and heavy bodies change amplitudes of the spike points and variances of the whole signals, respectively. And the unclear onset times indicate that real onset times are covered by noise. These problems make it rather difficult to pick onset times accurately [14].

To enhance picking accuracies of onset time for acoustic signals with noise, various hybrid methods had been proposed, e.g., STA/LTA- polarization-AIC [15], STA/LTA and kurtosis [16], improved MER (IMER) [17]. However, the picking accuracies of onset times by those hybrid methods were unreliable for the signals with strong noise. Recently, some joint methods with the wavelet analysis or empirical mode decomposition (EMD) could be found in some literatures, which greatly improved the picking accuracies of the onset times for noisy signals. GALIANA-MERINO et al [18] applied kurtosis method with stationary wavelet transform (SWT) to pick onset times of seismic signals from three different data sets. Although the method provided good onset estimations for signals with strong noise, the problem of spikes was not researched yet. GACI [19] used STA/LTA and MER methods with wavelet de-noising respectively to identify onset times of seismic signals with noise, the results showed wavelet-STA/LTA method had a better performance in 0-3 signal to noise ratios (SNRs). However, it was worse than wavelet-MER when SNRs varied from 10 to 15. HAFEZ et al [20, 21] applied the STA/LTA on the wavelet components to determine P-phase onset times. But the method was difficult for STA/LTA picker to determine an appropriate threshold value for different waveforms. Combined with STA/LTA picker and discrete wavelet transform (DWT), an improved Kurtosis method [22] was also applied to pick the onset times of micro-seismic signals with noise. It was fine to deal with the problem of spikes. But the picking range of Kurtosis picker needed to be selected by analysts, which has not universal applicability for different frequency signals. LI et al [23, 24] used the AIC method combined with EMD to detect the P-phase onset times of 1938 micro- seismic waveforms in Yongshaba mine. This method could pick signal onset times with unclear takeoffs and spikes accurately. However, it was not accurate to pick onset times of signals with heavy bodies.

In this paper, an improved joint method based on DWT, MER and AIC has been proposed to overcome the influence of spikes, heavy bodies and unclear takeoffs on onset picking. The brief mathematical descriptions on the DWT, MER and AIC are first given. Next, the implement detail of this improved joint method is presented. Last the improved joint method is tested on acoustic signals with different SNRs and waveforms. Its performance is compared against those of MER, AIC, DWT-MER and DWT-AIC.

2 Theoretical background of improved joint method

Improved joint method in this work is based on the DWT, MER and AIC. The DWT decomposes the signal at different scales, at every scale, the approximate and detail components are both obtained. For the noisy signal, noise is high frequency compared to the valid component, which is often mainly contained in the detail component at every scale. To reduce the noise interference, the approximate components are selected for subsequent picking tasks. In addition, the primary features in the signal are retained over several resolution scales. Hence, multiple approximate components need to be applied to characterizing the original signal. MER and AIC pickers can both recognize changes of signal amplitudes in time domain, but reactions of these two pickers on onset time are different. The AIC picker is more sensitive to onset time than the MER picker. But the AIC picker is also easier to be disturbed by noise than the MER picker. Consequently, the joint application of the MER and AIC pickers after the signal decomposed by the DWT, not only overcomes the noise interference but also keeps the sensitivity of onset picking. To better clarify the improved joint method, their theoretical backgrounds are exposed as follows:

2.1 Waveform decomposition with DWT theory

A band pass function ψ named as the mother wavelet regards t=0 as the center in time domain, possessing a zero mean and localization in time and frequency domains [25, 26]. The baby wavelet ψ_a,b can be obtained by dilation and translation of the mother wavelet:

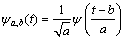                      (1)

where a and b are the scale and translation parameters, respectively; t is the time of dilation and translation. Generally, a and b are discretized by a=2^j and b=n·2^j. The resulting baby wavelet is given by

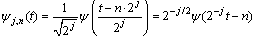    (2)

where j is the scale factor, j=0, 1, …, J-1 (J denotes the maximum decomposition level); n is the translation factor;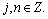According to the multi-resolution analysis [27], arbitrary function 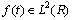can be expanded at the (j-1)th level by

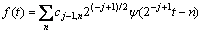           (3)

where c_j-1,n is the scale coefficient in the (j-1)th scale space. When the function f(t) is decomposed to the jth scale and wavelet spaces, the function is expressed by

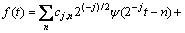
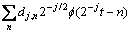                 (4)

where c_j,n is the scale coefficient in the jth scale space; d_j,n is the wavelet coefficient in the jth wavelet space; ψ(2^-jt-n) is the scale function; f(2^-jt-n) is the wavelet function. The c_j,n and d_j,n can be obtained by the convolution.

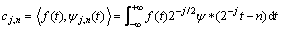 (5)

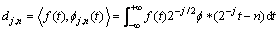 (6)

whereis the convolution symbol; ψ*(2^-jt-n) and f*(2^-jt-n) are the conjugate function of ψ(2^-jt-n) and f(2^-jt-n) respectively. Here f_j,n(t)= 2^-j/2f*(2^-jt-n). According to the two-scale equation, let t₁=2^-jt-n, ψ(2^-jt₁-n) and f(2^-jt₁-n) can be expressed by

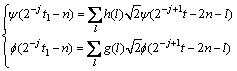       (7)

where h and g are low pass filter and high pass filter respectively. Let m=2n+l, Eq. (7) is updated by

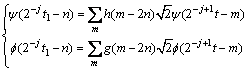     (8)

Based on Eqs. (5), (6) and (8), the c_j,n and d_j,n can be given by

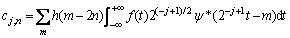
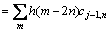                      (9)

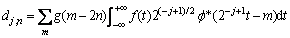
                    (10)

Within the maximum decomposition level, the approximate and detail components consist of c_j,n and d_j,n, respectively. Due to the effect of decomposition, the lengths of the c_j,n and d_j,n are compressed from the original signal, the single scale reconstruction thus must be conducted to make the lengths of c_j,n and d_j,n coherent with the original signal. The reconstructed approximate components are regarded as the following objects for onset picking.

2.2 Approximate onset picking with MER picker

The MER method [28] is an advanced energy-based method, calculating the energy density in the preceding and trailing windows of the sliding point. And the lengths of the pre-window and post-window should be equal. The energy ratio ER_(i) of the ith point for signal series x(t) (t=1, 2, …, N) is defined by

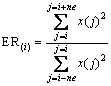                       (11)

where x(j) is the amplitude of the jth sample in signal series; ne is the number of samples in every energy window. Then the MER is calculated as follows:

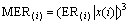                    (12)

The peak position of MER series is regarded as MER onset time and it usually appears slightly later than the real onset time for the property of the algorithm itself. Consequently, the MER picker could be applied to determining approximate onset time of acoustic signals.

2.3 Initial onset picking with AIC picker

To obtain the accurate onset time further, another picking method of onset time, the AIC picker [29-31] is also employed after the MER picker applied. The AIC picker is based on the concept that the intervals before and after onset time are two different stationary time series. Here AIC is represented as [32]:

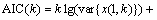
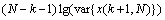            (13)

where k is the sliding point, N is the signal length, var{x(1, k)} is the variance of time series before the sliding point k, and var{x(k+1, N)} is the variance of time series after the sliding point k. To each selected component, the minimum position of AIC series before MER onset time, is regarded as initial onset time.

The whole picking process and parameter determination of the improved joint method.

3 Whole picking process and parameter determination of improved joint method

3.1 Whole picking process

The improved joint method takes advantage of the multi-scale property of the DWT, the stability of the MER picker and sensitivity of the AIC picker. First, the DWT is applied to obtaining the approximation components of the acoustic signal. Second, the MER picker is used to pick MER onset times of all selected approximate components. At the same time, the AIC series of the selected components are also obtained by the AIC picker. Then the minimum position of each AIC series before the MER onset time is regarded as the initial onset time of each selected component. Last, the average for initial onset times of all selected components is determined as the final onset time of the acoustic signal. The whole process of onset picking by the improved joint method is depicted in Figure 1 and the details are elaborated as follows:

Step 1: Import the original acoustic signal x(t) (t=1, 2, …, N), with a sampling frequency of 3 MHz.

Step 2: Decompose the acoustic signal x(t) into various components based on the DWT and then some better approximate components are selected for the subsequent onset picking. The selection details are explained in Section 3.2.

Step 3: Pick the approximate onset time of each selected component by the MER picker and obtain the AIC series of each selected component by the AIC picker, respectively.

Step 4: Determine the accurate onset time of each selected component. For each selected component, the minimum position of each AIC series between start time and the MER onset time is regarded as the accurate onset time.

Step 5: Calculate the final onset time of the acoustic signal. The average for accurate onset times of all selected components is calculated as the final onset time of the acoustic signal.

3.2 Parameter determination

In the picking process, the picking accuracies of onset times by MER picker depend on the selection of the window length. According to the previous experience, the length of MER window should be two to three times the cycle of a typical signal. To test the effect of window length on MER onset time, the window lengths with 60, 120, 180, 300, 600, 1200 samples are selected respectively to pick the onset times of 100 AE signals by MER picker. The results are displayed in Figure 2. The picking errors at horizontal axis are the difference between MER onset times and manual onset times. From Figure 2, no matter what the window lengths are, MER onset times are always later than manual onset times. With the increase of the window length, the number of events owning small picking errors reduces gradually, which indicates that the MER picker with window length of 60 samples can obtain the best picking accuracies of onset time. Hence, 60 samples are selected as the window length for MER picker.

The selection of decomposed components is also crucial to pick onset times of AE signals accurately. The selected components should not only reduce noise but also retain the onset time well. To a typical rock AE signal given in Figure 3(a), its eight approximate components are obtained. Then the onset time of each component is picked by the improved joint method, which is shown in Figure 3(b). By the results, the c6, c7 and c8 components have unclear onset times, so the higher decompositions thus do not need to be conducted. The c4 and c5 components have obvious onset times, but their valid compositions have been lost seriously compared to the original signal. At the same time, the c1, c2 and c3 components not only maintain the effective signal composition but also have the obvious onset times. Hence, the c1, c2 and c3 components are selected as subsequent picked components.

Moreover, the application of the DWT method needs the wavelet basis function. There are massive basis functions supplied for the DWT. To determine effects of wavelet basis function on picking accuracies of onset times, different wavelet basis functions are used by the improved joint method to pick onset times of the AE signal (Figure 3(a)), respectively. The picking results of onset times based on different basis functions are listed in Table 1. The onset times based on Harr, db3, db5, sym2, sym4, coif2 and coif4 wavelets are the 1002th, 1000th, 997th, 997th, 1002th, 1002th and 1002th points, respectively. The onset times based on db5 and sym2 are closest to the 966th point picked manually, which indicates that the db5 and sym2 are most suitable for the improved joint method among above basis functions. The db5 wavelet is selected in this work.

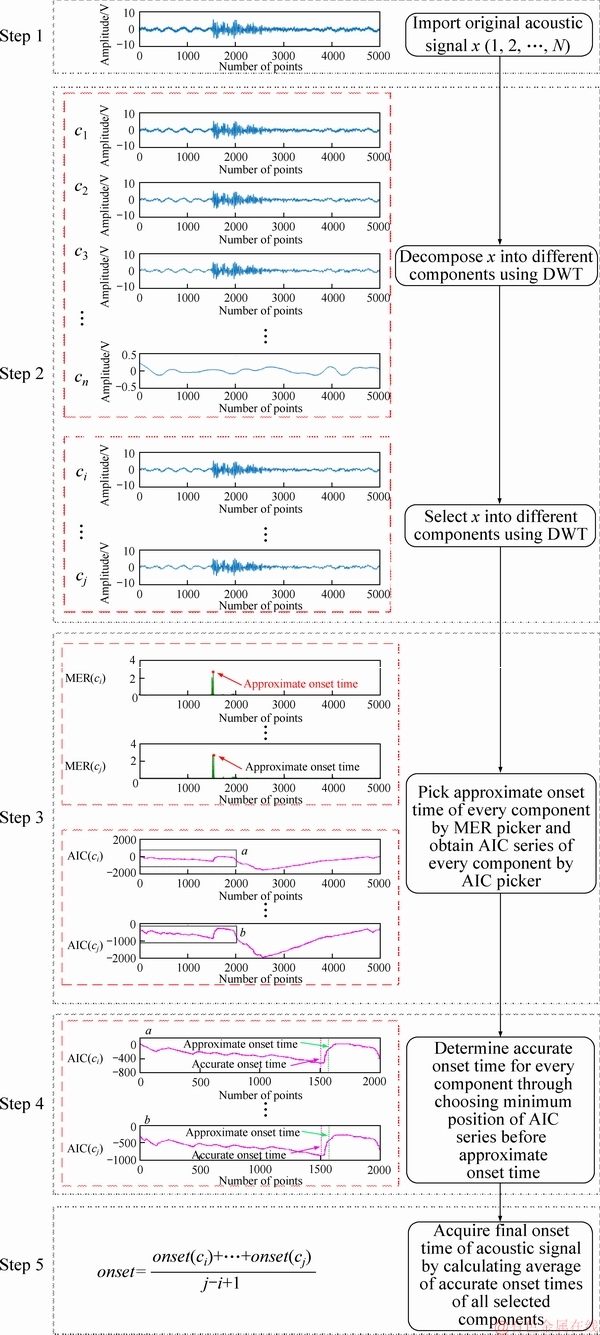
Figure 1 Onset picking process of an acoustic signal based on improved joint method

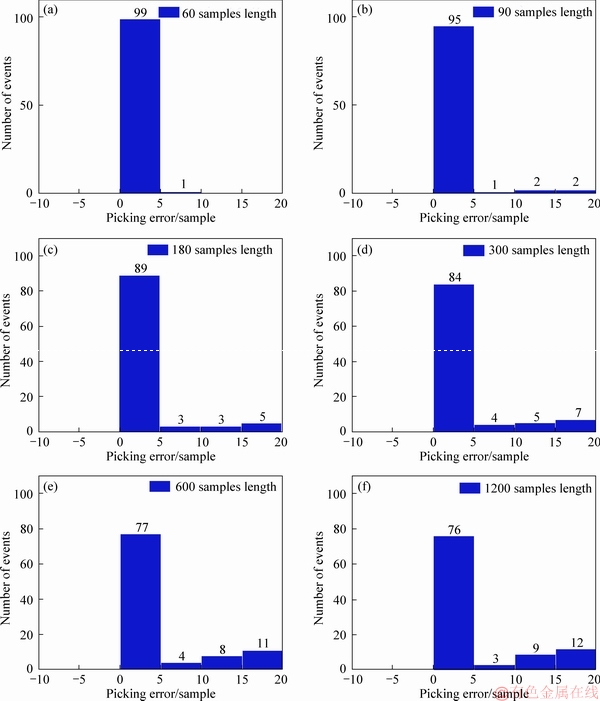
Figure 2 Number of events corresponding to different picking errors between manual onset times and MER onset times for 100 AE signals with different window lengths

4 Performance verification of improved joint method

4.1 SNR stability

SNR stability is an important index judging performance of the improved joint method, where SNR is defined as the ratio of the mean absolute amplitude after and before onset time. To obtain different SNRs, the acoustic signals are synthesized artificially through adding progressively larger amounts of random noise to a clean AE signal. Then onset times of these synthetic signals are picked by MER, AIC, DWT-AIC, DWT-MER and the improved joint methods, respectively. The results have been shown in Figure 4. It can be seen that the picking accuracies of onset times by MER picker decrease gradually with the reduction of SNR and the picking errors of onset times by AIC picker are always large no matter what SNR is. In addition,when SNR is 10, onset times of c₁, c₂ and c₃ components picked by DWT-MER method are the 935th, 936th and 934th points, respectively. Those picked by DWT-AIC method are the 935th, 936th and 934th points, respectively. Those picked by the improved joint method are the 933th, 932th and 931th points, respectively. So the final onset times by DWT-MER, DWT-AIC and the improved joint methods are the 935th, 3235th and 932th points, respectively. When SNR is 5, onset times of c₁, c₂ and c₃ components picked by DWT-MER method are the 1176th, 940th and 937th points, respectively. Those picked by DWT-AIC method are the 2694th, 2696th and 3129th points, respectively. Those picked by the improved joint method are the 933th, 931th and 929th points, respectively. The final onset times by DWT-MER, DWT-AIC and the improved joint methods thus are the 1017th, 2839th and 931th points, respectively. When SNR is 2, onset times of c₁, c₂ and c₃ components picked by DWT-MER method are the 1177th, 937th and 936th points, respectively. Those picked by DWT-AIC method are the 2701th, 2701th and 2704th points, respectively. Those picked by the improved joint method are the 936th, 935th and 934th points, respectively. Hence, the final onset times by DWT-MER, DWT-AIC and the improved joint methods are the 1016th, 2702th and 935th points, respectively. According to the picking results of onset times, when SNR is less than 10, the DWT-MER method is affected to such extent that the picking accuracies of onset times become worse. Meanwhile, the picking accuracies of onset times by DWT-AIC method are always poor no matter what SNR is. However, the picking results of onset times by the improved joint method keep always stable and are not affected by the variation of SNR. In addition, at each SNR, the picking result of onset time based on the improved joint method is always closest to the real onset time, which illustrates the improved joint method is more accurate than other methods.

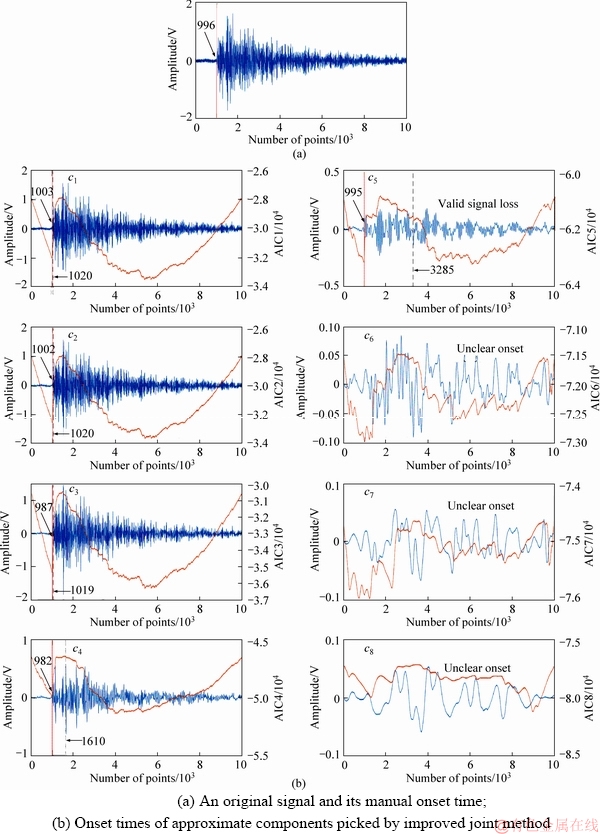
Figure 3 Onset times of an AE signal and its approximate components based on improved joint method:

Table 1 Effects of wavelet basis function for picking accuracy based on combined method

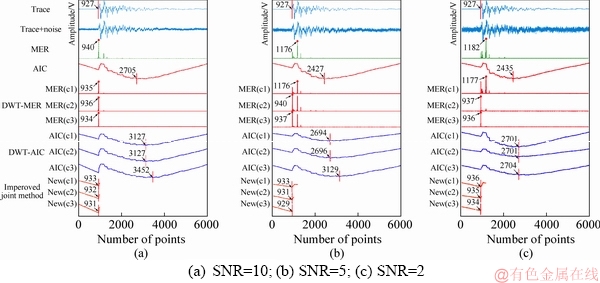
Figure 4 Results of picking onset times on synthetic trace with different SNRs by different methods:

4.2 Waveform adaptability

To test the waveform adaptability of the improved joint method, four typical AE signals with clear onset, unclear onset, spikes and heavy bodies, have been used. These AE signals are obtained from the AE monitoring system DS5-16C. At the same time, the AIC, MER, DWT-MER and DWT-AIC methods are also applied to picking the onset times of the four signals simultaneously. The picking results are depicted in Figures 5 and 6.

For a signal with clear onset time(Figure 5(a)), the onset times picked by the MER and AIC methods are the 1431th and 1429th points, respectively. The onset times of c₁, c₂ and c₃ components picked by DWT-MER method are the 1431th, 1431th and 1429th points, respectively. Taking an integer closest to average of these three onset times, the final onset time picked by this method is the 1430th point. The onset times of c₁, c₂ and c₃ components picked by DWT-AIC method are the 1429th, 1426th and 1423th points, respectively. The final onset time picked by this method is the 1426th point. The onset times of c₁, c₂ and c₃ components picked by the improved joint method are the 1429th, 1426th and 1423th points, respectively. The final onset time picked by this method is the 1426th point. Compared to the manual picking result, the five methods all obtain good picking accuracies. And the improved joint and DWT-AIC methods have best accuracies among the five methods.

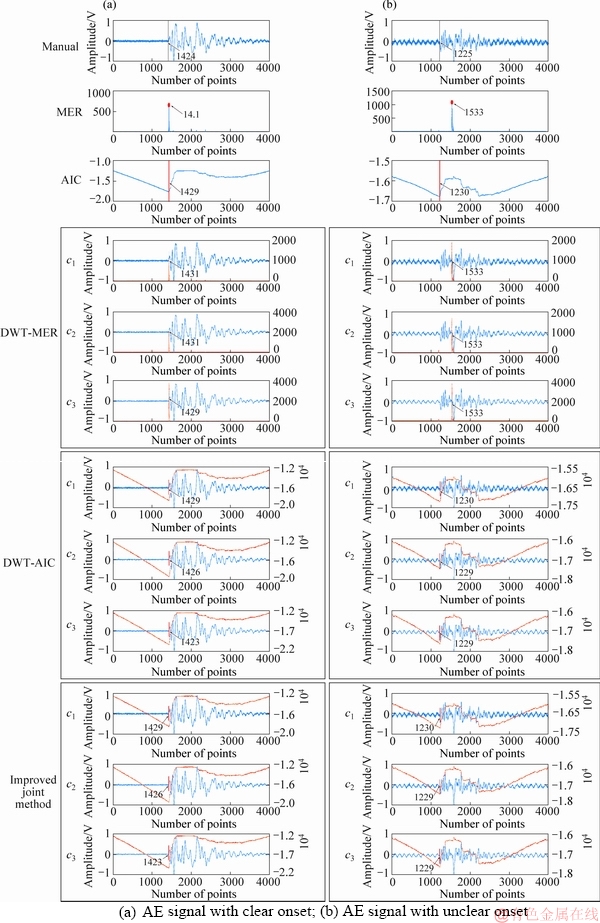
Figure 5 Onset time picked by manual, MER, AIC, DWT-MER, DWT-AIC and improved joint method for:(The dots, arrows and values in the MER picking are the onsets picked by the MER method, the lines (red and black lines), arrows and values in the other graphs are the onsets picked by the rest methods)

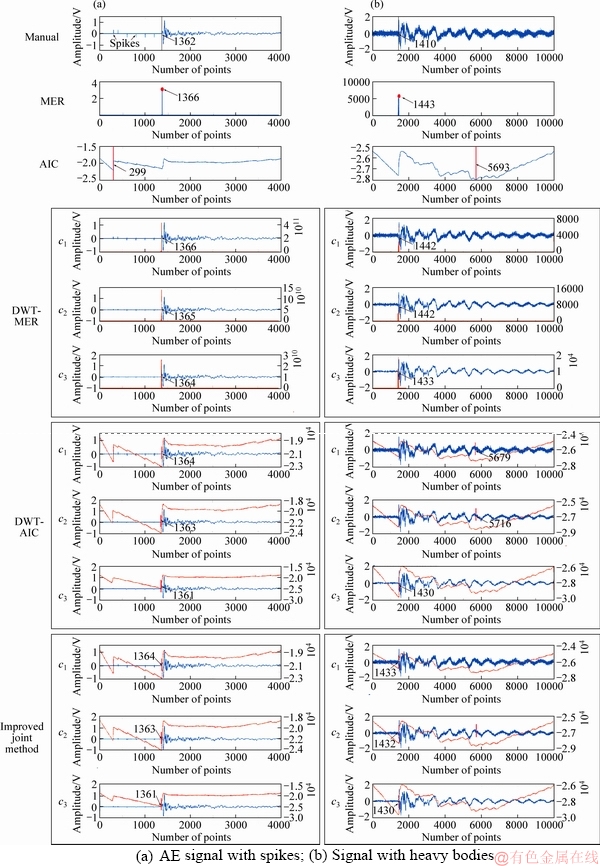
Figure 6 Onset time picked by manual, MER, AIC, DWT-MER, DWT-AIC and improved joint method for:(The dots, arrows and values in the MER picking are the onsets picked by the MER method, the lines (red and black lines), arrows and values in the other graphs are the onsets picked by the rest methods)

For a signal with unclear onset time (Figure 5(b)), the onset times picked by the MER and AIC methods are the 1533th and 1230th points, respectively. The all onset times of c₁, c₂ and c₃ components picked by DWT-MER method are the 1533th point. The final onset picked by this method is naturally the 1533th point. The onset times of c₁, c₂ and c₃ components picked by DWT-AIC method are the 1230th, 1229th and 1229th points, respectively. Taking an integer closest to average of these three onset times, the final onset time picked by this method is the 1229th point. The onset times of c₁, c₂ and c₃ components picked by the improved joint method are the 1230th, 1229th and 1229th points, respectively. The final onset time picked by this method is the 1229th point. Compared to the manual picking result, the MER and DWT-MER methods are affected by the uneven take off point. The other methods still have the ideal picking results, and the improved joint and DWT-AIC methods have best accuracies among the five methods.

For a signal with spikes (Figure 6(a)), the onset times picked by the MER and AIC methods are the 1366th and 299th points, respectively. The onset times of c₁, c₂ and c₃ components picked by DWT-MER method are the 1366th, 1365th and the 1364th points, respectively. The final onset picked by this method is the 1365th point. The onset times of c₁, c₂ and c₃ components picked by DWT-AIC method are the 1364th, 1363th and 1361th points, respectively. The final onset picked by this method is the 1363th point. The onset times of c₁, c₂ and c₃ components picked by the improved joint method are 1364th, 1363th and 1341th points, respectively. The final onset picked by this method is the 1363th point. Compared to the manual picking result, the AIC method are affected by the presence of the spikes. The other methods still have the good picking results, and the improved joint and DWT-AIC methods have best accuracies among the five methods.

For a signal with heavy bodies (Figure 6(b)), the picking times by the MER and AIC methods are the 1443th and 5663th points, respectively. The onset times of c₁, c₂ and c₃ components picked by DWT-MER method are the 1442th, 1442th and 1433th points, respectively. The final onset picked by this method is the 1439th point. The onset times of c₁, c₂ and c₃ components picked by DWT-AIC method are the 5679th, 5716th and 1430th points, respectively. The onset time picked by this method is the 4275th point. The onset times of c₁, c₂ and c₃ components picked by the improved joint method are the 1230th, 1229th and 1229th points, respectively. The final onset time picked by this method is the 1229th point. Compared to the manual picking result, the AIC and DWT-AIC methods are affected by the interference of the heavy bodies. The other methods still have the good picking results, and the improved joint method has best accuracies among the five methods.

Through the above analysis, the MER and DWT-MER methods are sometimes affected by the unclear onset time, the AIC method is easily disturbed by the spikes and heavy bodies, the DWT-AIC method is also interfered by the heavy bodies. It is satisfactory that no matter how the waveforms are, the improved joint method is always not affected, which illustrates that the improved joint method has better waveform adaptability.

5 Conclusions

An improved joint method with the DWT, MER and AIC methods has been proposed for the onset picking of acoustic signals in this paper. The improved joint method takes advantage of the multi-scale and decomposition ability of DWT, the sensitivity of AIC picker and the stability of the MER picker. To enhance the accuracies of onset picking, some parameters of the improved joint method have been discussed and determined. The c₁, c₂, c₃ components, db5 basis function and the window length of 60 samples are the best selection for this improved joint method. By the analysis of SNR stability and waveform adaptability for different methods of onset picking, the performance of the improved joint method is validated. On the SNR stability, the picking errors of onset times by AIC and DWT-AIC methods are always large no matter what SNR is. When SNR is less than 10, the MER and DWT-MER methods are affected to such extent that the picking accuracies of onset times become worse. The picking results of onset times by the improved joint method always keep stable and accurate. On the waveform adaptability, the MER and DWT-MER methods are affected by the unclear onset time, the AIC method is easily disturbed by the spikes and heavy bodies, the DWT-AIC method could be also disturbed by the heavy bodies. The improved joint method is always accurate and not affected by the spikes, heavy bodies and unclear onset. In conclusion, the improved joint method has better performance than other four methods mentioned.

References

[1] GE M. Efficient mine microseismic monitoring [J]. International Journal of Coal Geology, 2005, 64(1, 2): 44-56.

[2] ZHOU Zi-long, CHENG Rui-shan, RUI Yi-chao, ZHOU Jing, WANG Hai-quan. An improved automatic picking method for arrival time of acoustic emission signals [J]. IEEE Access, 2019, 7: 75568-75576.

[3] XU Nu-wen, DAI Feng, LI Biao, ZHU Yong-guo, ZHAO Tao, YANG Dian-sen. Comprehensive evaluation of excavation-damaged zones in the deep underground caverns of the Houziyan hydropower station, Southwest China [J]. Bulletin of Engineering Geology & the Environment, 2016, 76(1): 1-19.

[4] ZHOU Zi-long, ZHOU Jing, DONG Long-jun, CAI Xin, RUI Yi-chao, KE Chang-tao. Experimental study on the location of an acoustic emission source considering refraction in different media [J]. Scientific Reports, 2017, 7(1): 7472: 1-13.

[5] GOU Xian-tai, LI Zhi-min, QIN Na, JIA Wei-dong. Adaptive picking of microseismic event arrival using a power spectrum envelope [J]. Computers & Geosciences, 2011, 37(2): 158-164.

[6] ALVAREZ I, GARCIA L, MOTA S, CORTES G, BENITEZ C, de la ANGEL TORRE. An automatic P-phase picking algorithm based on adaptive multiband processing [J]. IEEE Geoscience & Remote Sensing Letters, 2013, 10(6): 1488-1492.

[7] ZHOU Zi-long, CHENG Rui-shan, CAI Xin, MA Dan, JIANG Chong. Discrimination of rock fracture and blast events based on signal complexity and machine learning [J]. Shock and Vibration, 2018: 9753028.

[8] MA Dan, MIAO Xie-xing, BAI Hai-bo, PU Hai, CHEN Zhan-qing, LIU Jiang-feng, HUANG Yan-hua, ZHANG Gui-ming, ZHANG Qi. Impact of particle transfer on flow properties of crushed mudstones [J]. Environmental Earth Sciences, 2016, 75(7): 593.

[9] DONG Long-jun, SUN Dao-yuan, LI Xi-bing, DU Kun. Theoretical and experimental studies of localization methodology for AE and microseismic sources without pre-measured wave velocity in mines [J]. IEEE Access, 2017, PP(99): 1-1. DOI: 10.1109/ACCESS.2017.2743115.

[10] DONG Long-jun, SHU Wei-wei, HAN Guang-jie, LI Xi-bing, WANG Jian. A multi-step source localization method with narrowing velocity interval of cyber-physical systems in buildings [J]. IEEE Access, 2017, PP(99): 1-1. DOI: 10.1109/ACCESS.2017.2756855

[11] ZHANG Zhi-zhen, GAO Feng, SHANG Xiao-ji. Rock burst proneness prediction by acoustic emission test during rock deformation [J]. Journal of Central South University, 2014, 21(1): 373-380.

[12] MA Da, WANG Jia-jun, CAI Xin, MA Xiao-tong, ZHANG Ji-xiong, ZHOU Zi-long, TAO Ming. Effects of height/ diameter ratio on failure and damage properties of granite under coupled bending and splitting deformation [J]. Engineering Fracture Mechanics, 2019, 220: 106640.

[13] MA Dan, DUAN Hong-yu, LI Xi-bing, LI Zhen-hua, ZHOU Zi-long, LI Tian-bin. Effects of seepage-induced erosion on nonlinear hydraulic properties of broken red sandstones [J]. Tunnelling and Underground Space Technology, 2019, 91: 102993.

[14] SHANG Xue-yi, LI Xi-bing, MORALES-ESTEBAN A, DONG Long-jun. Enhancing micro-seismic P-phase arrival picking: EMD-Cosine function based denoising with application to the AIC picker [J]. Journal of Applied Geophysics, 2017. DOI: https://doi.org/10.1016/j.jappgeo. 2017.09. 012.

[15] TAN Yu-yang, YU Jing, Yu, FENG Gang, HE Chuan. A combined method for automatic microseismic event detection and arrival picking [C]// SEG Annual Meeting. Denver: Society of Exploration Geophysicists, 2014: 2335-2340.

[16] LI Fang-yu, RICH, J, MARFURT, K J, ZHOU Huai-lai. Automatic event detection on noisy microseismograms [C]// SEG Annual Meeting. Denver: Society of Exploration Geophysicists, 2014: 2363-2367.

[17] LEE M, BYUN J, KIM D, CHOI J, KIM M. Improved modified energy ratio method using a multi-window approach for accurate arrival picking [J]. Journal of Applied Geophysics, 2017, 139: 117-130.

[18] GALIANA-MERINO J J, ROSA-HERRANZ J L, PAROLAI S. Seismic P-phase picking using a Kurtosis-based criterion in the stationary wavelet domain [J]. IEEE Transactions on Geoscience & Remote Sensing, 2008, 46(11): 3815-3826.

[19] GACI, S. The use of wavelet-based denoising techniques to enhance the first-arrival picking on seismic traces [J]. IEEE Transactions on Geoscience & Remote Sensing, 2014, 52(8): 4558-4563.

[20] HAFEZ A G, KHAN M T A, KOHDA T. Clear P-wave arrival of weak, events and automatic onset determination using wavelet filter banks [J]. Digital Signal Processing, 2010, 20(3): 715-723.

[21] HAFEZ A G, RABIE M, KOHDA T. Detection of precursory signals in front of impulsive p-waves [J]. Digital Signal Processing, 2013, 23(3): 1032-1039.

[22] LI Xi-bing, SAHNG Xue-yi, WANG Ze-wei, DONG Long-jun, WENG Lei. Identifying p-phase arrivals with noise: an improved kurtosis method based on DWT and STA/LTA [J]. Journal of Applied Geophysics, 2016, 133: 50-61.

[23] LI Xing-bing, SAHNG Xue-yi, MORALES- ESTEBAN A, WANG Ze-wei. Identifying P phase arrival of weak events: The akaike information criterion picking application based on the empirical mode decomposition [J]. Computers & Geosciences, 2017, 100: 57-66.

[24] LING Tong-hua, ZHANG Sheng, CHENG Qian-qian, LI Jie. Wavelet basis construction method based on separation blast vibration signal [J]. Journal of Central South University, 2015, 22(7): 2809-2815..

[25] LI Shun-ming, WANG Jin-rui, LI Xiang-lian. Theoretical analysis of adaptive harmonic window and its application in frequency extraction of vibration signal [J]. Journal of Central South University, 2018, 25(1): 241-250.

[26] GOUPILLAUD P, GROSSMANN A, MORLET J. Cycle-octave and related transforms in seismic signal analysis [J]. Geoexploration, 1984, 23(1): 85-102.

[27] MALLAT S G. A theory for multiresolution signal decomposition: The wavelet representation [J]. IEEE Computer Society, 1989, 11(7): 674-693.

[28] AKRAM J, EATON D W. A review and appraisal of arrival-time picking methods for downhole microseismic data [J]. Geophysics, 2014, 81(2): KS67-KS87.

[29] TAKANAMI T, KITAGAWA G. Estimation of the arrival times of seismic waves by multivariate time series model [J]. Annals of the Institute of Statistical Mathematics, 1991, 43(3): 407-433.

[30] SLEEMAN R, ECK T V. Robust automatic P-phase picking: an on-line implementation in the analysis of broadband seismogram recordings [J]. Physics of the Earth & Planetary Interiors, 1999, 113(1-4): 265-275.

[31] DIEHL T, DEICHMANN N, KISSLING E, HUSEN S. Automatic S-wave picker for local earthquake tomography [J]. Bulletin of the Seismological Society of America, 2009, 99(3): 1906-1920.

[32] ZHANG Hai-jiang, THURBER C, ROWE C. Automatic P-wave arrival detection and picking with multiscale wavelet analysis for single-component recordings [J]. Bulletin of the Seismological Society of America, 2003, 93(5): 1904-1912.

(Edited by HE Yun-bin)

中文导读

一种拾取含噪声发射信号到时的改进联合方法

摘要：自动方法难以精确地拾取带有突刺，重体和起跳不清晰声源信号的到时。为了解决该问题，基于离散小波变换(DWT)、修改能量比(MER)和赤池信息量准则(AIC)，提出一种改进的联合拾取方法。首先，应用DWT将信号分解成各个分量；其次，联合应用MER和AIC拾取所有被选择分量的初步到时，其中初步到时是MER到时之前的最小AIC位置；最后，计算所有初步到时的平均值并作为信号最终到时。通过不同信噪比和波形的声源信号测试验证改进的联合拾取方法，结果显示信噪比的变化不能影响改进的联合拾取方法的精度，此外，改进的联合方法能够精确地拾取带有突刺、重体和起跳不清晰声信号的到时。相比较其他四种方法，该方法有更强的信噪比稳定性和波形适应能力。

关键词：赤池信息量准则；修改能量比；离散小波变换；含噪声信号

Foundation item: Project(2015CB060200) supported by the National Basic Research Program of China; Project(41772313) supported by the National Natural Science Foundation of China; Project(2018zzts736) supported by the Independent Innovation Exploration Project of Central South University, China

Received date: 2018-04-07; Accepted date: 2018-09-05

Corresponding author: CHEN Lian-jun, PhD, Associate Professor; Tel: +86-13789870628; E-mail: creejxk@163.com; CHENG Rui- shan, PhD; Tel: +86-15364072560; E-mail: Chengruishan@csu.edu.cn