文章编号：1004-0609(2011)09-2216-07

相场法模拟强各向异性作用下二元合金枝晶生长

袁训锋, 丁雨田

(兰州理工大学 甘肃省有色金属新材料省部共建国家重点实验室 兰州 730050)

摘  要：基于Wheeler模型和Eggleston修正强界面能各向异性的方法，建立耦合溶质场和温度场的相场模型，模拟强界面能和界面动力学各向异性下Ni-Cu合金的枝晶生长过程。结果表明：两种各向异性均显著影响枝晶生长，在强界面动力学各向异性下，固相以类矩形方式沿á110?方向生长；在强界面能各向异性及同时存在两种各向异性下，固相以枝晶方式沿á100?方向生长，界面方向不连续，枝晶臂主枝尖端出现棱角。在各向异性强度取值相同情况下，仅有界面能各向异性时，á100?方向枝晶尖端温度梯度大，生长迅速，稳态生长速度比同时存在两种各向异性的大32.26%；仅有界面动力学各向异性时，á100?方向枝晶尖端温度梯度小且溶质浓度高，生长缓慢，稳态生长速度比同时存在两种各向异性的小48.92%。

关键词：二元合金；界面能各向异性；界面动力学各向异性；相场法；枝晶生长

中图分类号：TG146   文献标识码：A

Phase-field simulation of dendrite growth for

 binary alloy with strong anisotropy

YUAN Xun-feng, DING Yu-tian

(State Key Laboratory of Gansu Advanced Non-ferrous Metal Materials,

Lanzhou University of Technology, Lanzhou 730050, China)

Abstract：Based on the Wheeler model and the Eggleston regularization technique of strong anisotropy of interface energy, the phase-field model was built by coupling with the concentration field and temperature field. The dendrite growth process of Ni-Cu alloy with strong surface energy and kinetic anisotropy were simulated. The results show that the dendrite growth depends on the two kinds of anisotropies. Under the strong surface kinetic anisotropy condition, the melt solidifies grow along the á110? orientation and the crystals grow into a square-like. Under the strong surface energy anisotropy or having two kinds of anisotropies condition, the melt solidifies in a dendrite pattern grow along the á100? orientation and the variation of interface orientation discontinuity can lead to the corners form on the tip of dendrite. In the case of anisotropy strength with the same values, under the strong surface energy anisotropy condition, the thermal gradient along the á100? orientation is large, and makes the dendrite growth become fast, the tip velocity at steady state increases by about 32.26% compared with the case that having two kinds of anisotropies. Under the strong surface kinetic anisotropy condition, the thermal gradient along the á100? orientation is small and the concentration of solute is large, and makes the dendrite growth become slow, the tip velocity at steady state decreases by about 48.92% compared with the case that having two kinds of anisotropies.

Key words：binary alloy; surface energy anisotropy; surface kinetic anisotropy; phase-field; dendrite growth

过冷熔体中的枝晶生长是凝固科学中的一个基础问题，同时也是理解其它复杂凝固现象的前提^[1]。枝晶的形成过程是一个涉及到热量、质量和动量传输以及界面动力学和毛细作用效应相耦合的自由边界问题，采用理论分析方法进行研究会遇到巨大的数学困难，而传统试验方法又无法揭示枝晶结构形成的有关物理机理。随着计算科学的发展和凝固理论的完善，采用数值模拟技术研究过冷熔体中的枝晶生长已成为凝固微观组织研究的热点。

相场方法在模拟凝固过程中微观组织形成方面具有巨大的优势。相场法以Ginzburg- Landau理论为基础，通过引入序参量场把液固界面由尖锐界面拓展为弥散界面，使得在整个计算区域中所有变量都连续可微，并且可以使用统一的控制方程描述，不必区分相和界面^[2]。自LANGER^[3]第一次提出采用扩散界面模型研究凝固现象以来，经过国内外学者不懈努力，相场法模拟凝固微观组织经历了从二维到三维^[4-6]、从二元合金到多元合金^[7]、从单晶粒到多晶粒^[8-9]，从自由枝晶到定向凝固^[10]、从单相场到多相场^[11]、从无流场到包含流场^[12-15]的逐步深入的发展历程，使得模拟结果越来越接近真实凝固过程。在2001年，EGGLESTON等^[16]提出了修正强界面能各向异性的方法，从而解决晶向缺失问题，建立强界面能各向异性下的枝晶生长相场模型。KASAJIMA等^[17]和KIM等^[18]采用此相场模型研究了强各向异性强度下过冷纯Si枝晶生长特性。在国内，李俊杰等^[19]、ZHANG等^[20]和CHEN等^[21]采用修正的相场模型，对强界面能各向异性下的枝晶生长行为进行了模拟。赵达文    等^[22-23]采用有限元法求解相场方程研究了弱界面能和界面动力学各向异性下过冷熔体中的枝晶生长行为。到目前为止，很少见到有关强界面能和界面动力学各向异性下枝晶生长的报道，人们对强界面能和界面动力学各向异性作用下的枝晶生长行为仍缺乏了解。

本文作者基于Wheeler模型和Eggleston修正强界面能各向异性的方法，建立耦合溶质场和温度场的相场模型，模拟强界面能和界面动力学各向异性作用下Ni-Cu合金的枝晶生长过程。研究强界面能各向异性、强界面动力学各向异性及同时存在两种各向异性下的枝晶生长形貌、溶质和温度分布及á100?方向枝晶尖端的生长行为。

1  相场模型

1.1  相场控制方程

晶体原子按照特定对称性排列，导致固液界面能、界面动力学具有不同程度的各向异性。在枝晶生长过程中液固界面各向异性不仅决定枝晶生长方向，还在很大程度上影响枝晶生长行为^[24]。在液固界面上，通常界面能与界面动力学各向异性同时存在。在相场模型中与界面能相关的是弥散界面厚度ε(θ)，与界面动力学效应相关的是原子驰豫时间τ(θ).这里选择界面各向异性具有四重对称性，即弥散界面厚度ε(θ)=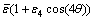、原子驰豫时间τ(θ)= τ₀(1+ε_kcos(4θ))²，其中，θ为界面法向与X正方向之间的夹角，ε₄和ε_k分别为界面能和界面动力学各向异性强度。

界面能各向异性对平衡形状的影响可以用Gibbs-Thomson方程描述：

ε(θ)+ε′′(θ)=(f ^L - f ^S)/R(θ)=1-15ε₄cos(4θ)          (1)

式中：R(θ)为固液界面的曲率半径，f ^L和f ^S分别为液相和固相的自由能密度。在弱界面能各向异性时(ε₄＜1/15)，方程的两边都为正，枝晶形貌光滑连续；在强界面能各向异性时(ε₄＞1/15)，方程左边为负，导致出现缺失方向，界面变的不连续，凹下去的部分出现耳子。

为了模拟强界面能各向异性下的枝晶生长，必须将耳子消除。采用EGGLESTON等^[16]的方法修正缺失方向得到的界面厚度，如下：

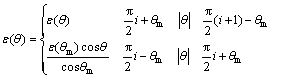  (2)

式中：i=0~3，θ_m为平衡形貌出现耳子时的角度，可以通过下式求得。

                (3)

基于WHEELER等^[15]的相场模型和EGGLESTON  等^[16]的修正方法建立了强界面能各向异性作用下枝晶生长的修正相场方程。

当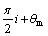≤≤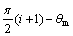，i=0~3时，

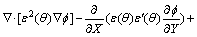
                      (4)

当＜＜，i=0，2时，

                           (5)

当＜＜，i=1，3时，

                           (6)

式中：Φ=0代表固相，Φ=1代表液相，在固/液界面上Φ在0→1之间连续变化；温度u，时间t和距离X、Y均为无量纲变量且u=(T-T_m)/(T_m-T₀)，t=t′/(ω²/κ)，X= X′/ω，Y=Y′/ω；Ω=c_p(ΔT+m_L(x-x₀))/L为无量纲过冷度；α=(ωL²)/(12c_pσT_m)为系统的物理参量；m=μσT_m/(κL)为界面动力学系数；=δ/ω为与界面层厚度有关的参量；T为热力学温度；T_m为熔点；T₀为系统初始温度；ΔT为热过冷度；X′、Y′为距离；δ为界面层厚度；ω为参考长度；t′为时间；κ为热扩散率；μ为界面迁移率；m_L为液相线斜率；c_p为定压比热容；L为单位体积的结晶潜热；σ为界面能；x₀为过冷熔体初始浓度(摩尔分数)；x为熔体实际浓度(摩尔分数)。

1.2  温度场控制方程

温度场控制方程为

                        (7)

式中：p′(Φ)为势函数p′(Φ)= Φ²(10-15Φ+6Φ²)对Φ的导数。

1.3 溶质场控制方程

溶质场控制方程为

                 (8)

式中：D′为有效溶质扩散系数。如果D_s和D_l表示固液相的溶质扩散系数；k₀为溶质平衡分配系数。D′可表示为

。

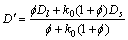2  计算方法

2.1  相场参数及材料物性参数的取值

选择Ni-Cu作为模拟对象，结合Ni-Cu的物性参数，使用相场法对过冷合金熔体中的强界面能和界面动力学各向异性作用下的枝晶过程进行模拟。本研究所需的Ni-Cu合金参数及模拟参数值如下：T_m=1 594.5 K，L=2 100 J/cm³，c_p= 4.83 J/cm³K，σ=3.38×10^-5 J/cm²，κ=0.27 cm²/s，D_s=1.0×10^{-9 cm2}/s，D_l=1.0×10^{-5 cm2}/s，μ=175.3 cm/Ks，ω=2.1×10^{-4 cm}，m_L=0.821 1，k₀=0.86，α=419，m=0.017，=0.005，τ₀=1.0，ε₄ =0.08，ΔT=0.1，θ_m=0.258，x₀=40.38%，ΔX=ΔY=0.005，Δt=2.0×10^-5。

2.2  数值计算方法

对于传输方程(7)采用交替隐式格式求解，控制方程(4)~(6)和(8)同时采用显示差分格式求解。由于温度场方程所采用的交替隐式格式具有任意的稳定性，整个计算过程的稳定性受以下条件约束：

＜                                (9)

式中：Δt为时间步长，ΔX=ΔY为空间步长， m′=max(D_l，m)，k′为考虑方程中非线性项而设计的修正系数，一般取1~2。

2.3  初始条件和边界条件

开始计算时假设网格数为R的球形初始晶核位于充满均匀过冷合金熔体的中心(X₀, Y₀)，即：

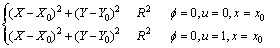  (10)

在计算区域的边界上，相场、温度场、溶质场采用Neumann条件。

3  结果与分析

3.1  强各向异性下的枝晶形貌

图1所示为Ni-Cu40.38%合金在不同各向异性作用下ΔT为0.1时的枝晶生长形貌。模拟计算网格数为800×800，图1显示为模拟中心400×400区域。从图1(a)可以看出，在强界面能各向异性作用下，固相以枝晶方式沿á100?方向生长，枝晶臂主枝细长，根部明显颈缩，并且由于某些方向的生长消失，界面方向不连续，枝晶臂主枝尖端出现棱角。在强界面动力学各向异性作用下，固相沿á110?方向生长，如图1(b)所示，主枝不发达，整体为类矩形形貌。在强界面能和界面动力学各向异性共同作用下，固相以枝晶方式沿á100?方向生长，如图1(c)所示，枝晶臂主枝发达，尖端出现棱角，根部无明显颈缩现象。

3.2  强各向异性下的枝晶溶质分布

图2所示为图1中不同各向异性作用下枝晶相场形貌对应的溶质分布。为了方便比较分析，对强界面能各向异性、强界面动力学各向异性及同时存在强界面能和界面动力学各向异性作用下的溶质分布采用统一的标尺，即相同颜色对应同一溶质浓度值。由图2可以看出，溶质分布情况与枝晶形貌是相吻合的。从图2可以看出，由于在凝固过程中存在溶质再分配，先凝固的枝晶主枝中心对应的溶质浓度最低，而液相中溶质的扩散速度小于枝晶生长速度，凝固析出的溶质不能充分扩散到液相中，从而大量溶质富集在枝晶臂前沿，其溶质浓度高。枝晶臂根部存在微观偏析，各枝晶臂的溶质扩散层分布相同。

图3所示为图2中的枝晶纵向主轴方向溶质分布情况。从图3可以看出，由于Ni-Cu合金的固液界面溶质平衡分配系数小于1，枝晶生长速度愈大，实际的固液界面溶质分配系数也越大，界面能各向异性为0.08时的枝晶生长速度比界面能和界面动力学各向异性均为0.08时的大，故在仅有界面能各向异性时的固相及固液界面前沿溶质浓度比界面能和界面动力学各向异性均存在时的要高。界面动力学各向异性为0.08时的固相及固液界面前沿溶质浓度最高，这是由于只有界面动力学各向异性时，在á110?方向原子的驰豫时间最小，固相沿á110?方向生长快，而在纵向主轴á100?方向原子驰豫时间长，其生长缓慢，溶质富集严重，溶质浓度高。总之，á100?方向的固相及固液界面前沿溶质浓度在仅有界面动力学各向异性时的最高，仅有界面能各向异性时次之，界面能和界面动力学各向异性均存在时最低。

3.3  强各向异性下的枝晶温度分布

图4所示为图1中不同各向异性作用下枝晶相场形貌对应的温度分布。为了方便比较分析，对3种情况下的温度分布采用统一的标尺，即相同颜色对应同一温度值。从图4中可以看出，枝晶周围由等温线包围，枝晶臂尖端等温线紧实，温度梯度大，其生长速度快；枝晶臂之间的区域等温线稀疏，温度梯度小，其生长缓慢。在界面能各向异性为0.08时，枝晶的4个尖端生长迅速，枝晶臂发达，等温线为类星形；在界面动力学各向异性为0.08时，4个优先生长方向的生长优势不明显，各向异性程度较弱，等温线为类球形；在界面能和界面动力学各向异性均为0.08时，4个优先生长方向上枝晶臂优先生长，等温线为类矩形。 图5所示为图4中的枝晶纵向主轴方向温度分布情况。从图5中可以看出，曲线中心平坦部分对应已凝固的枝晶固相，温度较高，温度梯度小；固相两侧为固液界面及液相，在固液界面上，曲线斜率最大，温度梯度最大，随后温度梯度减小。在仅有界面能各向异性时，á100?方向枝晶尖端固液界面温度梯度最大，枝晶生长最快；在仅有界面动力学各向异性时，á100?方向枝晶尖端固液界面温度梯度最小，枝晶生长最慢；在界面能和界面动力学各向异性均存在时，á100?方向枝晶尖端固液界面温度梯度和枝晶生长速度位于二者 之间。

图1   Ni-40.38%Cu合金在不同各向异性下ΔT为0.1时的枝晶生长形貌

Fig.1  Simulated dendrite morphologies of Ni-40.38%Cu alloy with different anisotropy at melt undercooling of ΔT=0.1:        (a) ε₄=0.08; (b) ε_k=0.08; (c) ε₄=ε_k=0.08

图2  Ni-40.38%Cu合金在不同各向异性下ΔT为0.1时的枝晶溶质分布

Fig.2  Dendrite distribution of solvend of Ni-40.38%Cu alloy with different anisotropy at melt undercooling of ΔT=0.1: (a) ε₄=0.08; (b) ε_k=0.08; (c) ε₄=ε_k=0.08

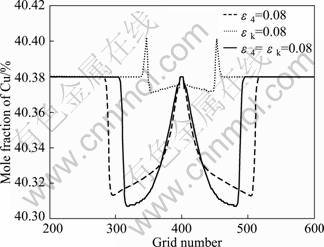
图3 不同各向异性下枝晶纵向主轴方向的溶质分布曲线

Fig.3  Solute distribution of dendrite along longitudinal principal axis at different anisotropy

图4  Ni-40.38%Cu合金在不同各向异性下ΔT=0.1时的枝晶温度分布

Fig.4  Temperature distribution of dendrite of Ni-40.38%Cu alloy with different anisotropy at melt undercooling of ΔT=0.1: (a) ε₄=0.08; (b) ε_k=0.08; (c) ε₄=ε_k=0.08

图5  不同各向异性下枝晶纵向主轴方向温度分布曲线

Fig.5  Temperature distribution of dendrite along longitudinal principal axis at different anisotropy

3.4 强各向异性作用下枝晶的尖端行为

为了定量分析强各向异性对枝晶生长行为的影响，本文作者计算了在仅有界面能各向异性和仅有界面动力学各向异性情况下，á100?方向枝晶尖端生长速度，尖端溶质摩尔分数和尖端温度随时间的变化关系，并与界面能和界面动力学各向异性均存在情况下进行了对比，结果见图6。

从图6可以看出，在凝固初始阶段，驱动枝晶生长的过冷度为初始过冷度，在枝晶尖端附近的初始温度梯度大，结晶潜热向过冷熔体中扩散速度大，枝晶尖端以较快的速度生长。随着生长过程的进行，热量在凝固前沿不断积累，热扩散边界层厚度逐渐增加，温度梯度不断减小，使得热扩散速度降低，枝晶尖端生长速度逐渐降低^[22]。同时，由于枝晶尖端生长速度降低，实际的固液界面溶质分配系数减小，导致仅有界面能各向异性及界面能和界面动力学各向异性均存在的á100?方向枝晶尖端溶质浓度降低。而仅有界面动力学各向异性时á100?方向枝晶尖端溶质浓度不断增加，这是由于á100?方向原子驰豫时间长，该方向生长缓慢，随着枝晶生长，溶质的富集越来越严重。经过一段时间后，溶质和潜热在界面前沿的释放与通过扩散的迁移基本达到动态平衡，枝晶尖端生长速度、溶质浓度和温度逐渐趋于稳定。在仅有界面能各向异性时的á100?方向枝晶尖端稳态生长速度和溶质摩尔分数分别比界面能和界面动力学各向异性均存在时的大32.26%和0.01%，稳态温度比界面能和界面动力学各向异性均存在时的低13.35%；在仅有界面动力学各向异性时的稳态生长速度比界面能和界面动力学各向异性均存在时的小48.92%，稳态溶质摩尔分数和稳态温度分别比界面能和界面动力学各向异性均存在时的高0.1%和35.17%。

图6  枝晶尖端生长速度、尖端温度和尖端溶质浓度与凝固时间的关系

Fig.6  Relationship among tip velocity (a), tip solute concentration (b) and tip temperature (c) and time for dendrite growth

4  结论

1)基于Wheeler模型和Eggleston修正强界面能各向异性的方法，建立耦合溶质场和温度场的相场模型，再现Ni-Cu合金强界面能和界面动力学各向异性下的枝晶生长过程。

2)在强界面动力学各向异性作用下，固相沿á110?方向生长，整体为类矩形形貌；在强界面能各向异性及同时存在强界面能和界面动力学各向异性作用下，固相以枝晶方式沿á100?方向生长，界面方向不连续，枝晶臂主枝尖端出现棱角。

3) 在各向异性强度取值相同的情况下，仅有界面动力学各向异性时的á100?方向枝晶尖端溶质浓度最高；仅有界面能各向异性时的á100?方向枝晶尖端溶质浓度次之；界面能和界面动力学各向异性均存在时的á100?方向枝晶尖端溶质浓度最低。

4) 在界面能各向异性强度为0.08时，á100?方向枝晶尖端枝晶温度梯度大，生长迅速，稳态生长速度比界面能和界面动力学各向异性强度均为0.08的大32.26%；在界面动力学各向异性强度为0.08时，á100?方向枝晶尖端温度梯度小，生长缓慢，稳态生长速度比界面能和界面动力学各向异性强度均为0.08的小48.92%。

REFERENCES

[1] KURZ W, FISHER D J. Fundamentals of solidification [M]. Switzerland: Trans Tech, 1998: 45.

[2] CAGINALP G, FIFE P. Higher-order phase field models and detailed anisotropy[J]. Phys Rev B, 1986, 34(7): 4940-4943.

[3] LANGER J S. Direction in condensed matter physics[M]. Singapore: World Science, 1986: 164.

[4] KARMA A, RAPPEL W J. Quantitative phase-field modeling of dendritic growth in two and three dimensions[J]. Phys Rev E, 1998, 57(4): 4323-4349.

[5] 赵红兆, 荆 涛, 柳百成. 铝合金三维枝晶生长相场模拟[J]. 金属学报, 2005, 41(5): 491-495.
ZHAO Hong-zhao, JING Tao, LIU Bai-cheng. Simulation of 3D dendritic growth of aluminum alloy by phase field model[J]. Acta Metall Sin, 2005, 41(5): 491-495.

[6] 朱昌盛, 冯 力, 王智平, 肖荣振. 三维枝晶生长的相场法数值模拟研究[J]. 物理学报, 2009, 58(11): 8055-8061.
ZHU Chang-sheng, FENG Li, WANG Zhi-ping, XIAO Rong-zhen. Numerical simulation of three-dimensional dendritic growth using phase-field method[J]. Acta Phys Sin, 2009, 58(11): 8055-8061.

[7] ODE M, LEE J S, KIM W T. Phase-field model for solidification of ternary alloys[J]. ISIJ International, 2000, 40(9): 870-876.

[8] SUN Q, ZHANG Y T, CUI H X, WANG C Z. Phase field modeling of multiple dendrite growth of Al-Si binary alloy under isothermal solidification[J]. China foundry, 2008, 5(4): 265-267.

[9] FENG L, WANG Z P, ZHU C S, LU Y. Phase-field model of isothermal solidification with multiple grain growth[J]. Chin Phys B, 2009, 18(5): 1985-1990.

[10] TAKAKI T, FUKUOKA T, TOMITA Y. Phase-field simulation during directional solidification of a binary alloy using adaptive finite element method[J]. J Cryst Growth, 2005, 283(1/2): 263-278.

[11] TIADEN J, NESTLER B, DIEPERS H J, STEINBACH I. The multiphase-field model with an integrated concept for modeling solute diffusion[J]. Physica D, 1998, 115(1/2): 73-86.

[12] TONG X, BECKERMANN C, KARMA A. Velocity and shape selection of dendritic crystals in a forced flow[J]. Phys Rev E, 2000, 61(1): 49-52.

[13] CHEN Z, CHEN C L, HAO L M. Numerical simulation of succinonitrite dendritic growth in a forced flow[J]. Acta Metall Sin (Engl Lett), 2008, 21(6): 444-450.

[14] 龙文元, 吕冬兰, 夏 春, 潘美满, 蔡启舟, 陈立亮. 强迫对流影响二元合金非等温凝固枝晶生长的相场法模拟[J]. 物理学报, 2009, 58(11): 7802-7808.
LONG Wen-yuan, L? Dong-lan, XIA Chun, PAN Mei-man, CAI Qi-zhou, CHEN Li-liang. Phase field simulation of non-isothermal solidification dendrite growth of binary alloy under the force flow[J]. Acta Phys Sin, 2009, 58(11): 7802-7808.

[15] WHEELER A A, MURRAY B T, SCHAEFER R J. Computation of dendrites using a phase field model [J]. Physica D, 1993, 66(1/2): 243-262.

[16] EGGLESTON J J, MCFADDEN G B, VOORHEES P W. A phase-field model for highly anisotropic interfacial energy[J]. Physica D, 2001, 150(1/2): 91-103.

[17] KASAJIMA H, NAGANO E, SUZUKI T, KIM S G, KIM W T. Phase-field modeling for facet dendrite growth of silicon[J]. Science and Technology of Advanced Materials, 2003, 4(6): 553-557.

[18] KIM S G, KIM W T. Phase field modeling of dendrite growth with high anisotropy[J]. Journal of Crystal Growth, 2005, 275(1/2): 355-360.

[19] 李俊杰, 王锦程, 杨根仓. 相场法模拟界面能各向异性对枝晶生长行为的影响[J], 自然科学进展, 2005, 15(11): 1312-1317.
LI Jun-jie, WANG Jin-cheng, YANG Gen-cang. Phase field modeling of dendritic growth with high interfacial energy anisotropy[J]. Progress in Natural Science, 2005, 15(11): 1312-1317.

[20] ZHANG G W, HOU H , CHENG J. Phase field model for strong anisotropy of kinetic and highly anisotropic interfacial energy[J]. Transactions of Nonferrous Metals Society of China, 2006, 16(Z2): 307-313.

[21] CHEN Z, CHEN C L, HAO L M. Numerical simulation of facet dendrite growth[J]. Transactions of Nonferrous Metals Society of China, 2008, 18(4): 938-943.

[22] 赵达文, 李金富. 相场模型模拟液固界面各向异性作用下自由枝晶生长[J]. 物理学报, 2009, 58(10): 7094-7100.
ZHAO Da-wen, LI Jin-fu. Phase-field modeling of the effect of liquid-solid interface anisotropies on free dendritic growth[J]. Acta Phys Sin, 2009, 58(10): 7094-7100.

[23] 赵达文, 李金富. 相场法模拟动力学各向异性对过冷熔体中晶体生长的影响[J]. 金属学报, 2009, 45(10): 1237-1241.
ZHAO Da-wen, LI Jin-fu. Phase-field simulation of the effect of kinetic anisotropy on crystal growth in undercooled melts[J]. Acta Metall Sin, 2009, 45(10): 1237-1241.

[24] LANGER J S. Existence of needle crystals in local models of solidification[J]. Phys Rev A, 1986, 33(1): 435-441.

(编辑 何学锋)

基金项目：兰州市科技局资助项目(2009-1-9)；兰州理工大学博士基金资助项目(SB01200606)

收稿日期：2010-08-04；修订日期：2011-01-15

通信作者：丁雨田，教授，博士；电话：0931-2757285；E-mail: dingyt @lut.cn