
DOI: 10.11817/j.issn.1672-7207.2021.03.016
针对网级评估的区域桥梁退化建模与演绎应用
夏烨1,雷晓鸣1,王鹏1, 2,孙利民1, 3
(1. 同济大学 桥梁工程系,上海,200092;
2. 上海临港经济发展(集团)有限公司,上海,201306;
3. 同济大学 土木工程防灾减灾国家重点实验室,上海,200092)
摘要:针对区域桥梁网级评估和管养策略优化的问题,系统地提出网级状态评估与管养策略优化框架,建立区域桥梁状态退化预测方法,实现桥梁状态在不同维修策略下的动态预测,解决路网桥梁管养策略的多目标优化问题。首先,从路网数据库中提炼得到用于桥梁状态预测的特征子集,选用合适的二次转码技术以适应人工神经网络的训练;然后,引入代价敏感型训练误差,通过模型选择得到最优桥梁退化模型,并用实测数据进行了效果验证;最后,通过控制各部位维修记录的输入,借助已有退化模型对单体桥梁在不同维修策略下的状态变化进行动态预测,进而拓展至整个桥梁路网。为统筹考虑区域路网的安全指标和费用指标,采用带精英策略的非支配排序遗传算法对网级评估结果进行分析和提炼,研究结果表明:该方法可建立基于神经网络的退化模型,可实现考虑维修的桥梁状态评估及预测。
关键词:桥梁工程;网级评估;神经网络;区域桥梁;退化模型;遗传算法
中图分类号:TU997 文献标志码:A
文章编号:1672-7207(2021)03-0828-11
Degradation modeling and application of regional bridges for network-level assessment
XIA Ye1, LEI Xiaoming1, WANG Peng1, 2, SUN Limin1, 3
(1. Department of Bridge Engineering, Tongji University, Shanghai 200092, China;
2. Shanghai Lingang Economic Development (Group) Co. Ltd, Shanghai 201306, China;
3. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China)
Abstract: To effectively assess the bridge condition, predict the degradation and optimize the management and maintenance strategy at the regional level, the framework of network-level condition assessment and optimization of management and maintenance strategy was proposed. The regional bridge condition degradation prediction methods and network-level management and maintenance optimization strategy were established, and multi-objective management strategy was optimized. Firstly, the selected features were extracted from road network database, and the appropriate transcoding technology was selected to adapt to artificial neural network. Then, the cost-sensitive training error was introduced, and the optimal bridge degradation model was obtained by model selection. After that, the condition of each bridge in the road network using different maintenance strategies were predicted with the proposed degradation models. In order to consider the structural safety and total cost of the road network, the genetic algorithm to analyze and refine the road network management and maintenance strategy was selected.
Key words: bridge engineering; network-level assessment; neural network; regional bridges; degradation model; genetic algorithm
桥梁是交通路网的枢纽。路网中,中小跨径桥梁占据了主体地位。截至2017年,全国公路桥梁超过80万座,其中,近90%的桥梁为中小跨径桥梁[1],大批老旧桥梁的结构受损和退化趋于显著,安全隐患与日俱增,针对运营桥梁的性能评价、退化预测及维修管养策略的合理制定迫在眉睫。在长年运营过程中,传统的桥梁检测手段为管养单位和科研机构积累了丰富而宝贵的资料,其对揭示结构的退化机理,挖掘退化共性特征及制定预防性管养策略等具有重要的指导意义[2]。然而,现行的检测评估方式大多仅限于对单体桥梁的分析和管养,未形成路网中时空的联通[3]。如果能以蕴含时空关系的检测数据为基础,借助数据挖掘技术提炼区域中小跨径桥梁的退化规律,开发路网级桥梁的管理和评估方法,则可较清晰地预测桥梁运营状态,明确桥梁状态的影响因素及程度,显著提高桥梁管理水平[4-5]。在运营管养中,面对桥梁路网产生的大量原始数据,从中提炼出桥梁退化模型来计算未来结构行为及状态是一个有效的预测途径。依据模型的种类可以分为3种:确定性模型、随机模型和机器学习模型。确定性模型使用较简单的数学公式描述桥梁退化行为,成为早期主要的退化模型[6]。虽然面向大规模路网预测与评估时具有较高的效率,但缺陷亦十分明显,如欠缺不确定性、仅能预测总体平均结果等[7]。随机模型则将随机过程的相关理论应用于上述问题,其中Markov模型的应用最为广泛,它通过定义结构状态的转移概率来模拟退化[8]。虽然该模型考虑了退化中的不确定性及当前状态对未来的影响,但仍依然存在局限[9]:1) 假定的转移时间间隔离散、样本数恒定、转移概率固定等往往是不科学的;2) 一阶Markov模型认为结构未来状态仅与当前状态有关,而与历史无关,这与实际不符。此外,上述2类模型均难以考虑加固、维修等过程对退化模式的影响,同时,也难以考虑不同构件在退化期间的相互作用。机器学习模型可采用事例推理、决策树、神经网络等方法描述桥梁退化行为,相比前述模型,其更具优势,且局限更少。MORCOUS[10]率先利用事例推理法建立基础设施的退化模型,表征了桥面板的未来状态与其物理特性、运营状况、养护记录等方面的关系。KIM等[11]又加入了桥龄、交通量等参数补充了结构特性预测模型。李龙祥等[12]基于密歇根州桥梁数据库,综合对比了神经网络、模糊推理、支持向量机等多种算法对桥墩构件的预测效率。ALIPOUR等[13]采用决策树和随机森林对桥梁群体的荷载评级进行了学习和预测,取得了较高的准确度,对工程实践也有一定参考。在以往的研究中,虽然在建立退化模型时考虑了结构特性、环境因素、交通信息等相关变量,但大部分研究主要着眼于桥梁构件或单体,并还存在以下不足:1) 桥梁路网作为多层次研究主体,未考虑构件或单体间的逻辑关系;2) 区域内各属性的相互作用和耦合的非线性关系还不充分;3) 维修与养护等可以对结构性能产生较大影响的作用未能在模型中明确量化;4) 网级评估的结论如何在区域内有效演绎并转化为决策依据,也未能有效实现。在区域桥梁管养策略优化中,绝大多数只能提供单体的优化方案,未能实现区域内桥梁管养的统筹规划。FRANGOPOL等[14]首先建立了仅考虑桥梁损伤的区域网级评估分析框架,将系统与结构的多层次性能包含在内,为区域策略指定提供了参考。在提高策略优化效率上,两阶段随机动态规划法(DPM)[15]利用单体权重系数有效平衡了单体维修与总体性能之间的关系,但权重的合理取值制约了该方法的应用。而带精英策略的非支配排序遗传算法(NSGA-II)[16]能在根据管养者偏好给出各类最优方案的同时进一步提高策略优化的效率。但在以往文献在桥梁管养策略优化中,对结构性能退化尤其是维修行为对桥梁状态的影响欠考虑。为此,本文作者融合人工神经网络(ANN)预测模型及NSGA-II优化算法,提出网级状态评估与管养策略优化框架,以量化桥梁状态与各特征属性间的关系并解决路网桥梁管养策略的优化问题。基于河北省交通路网信息数据库,提取数据库中的关键属性及数据集进行神经网络训练与验证,建立目标区域内桥梁状态的退化模型。采用该模型演绎子路网的桥梁,对桥梁未来状态和发展趋势进行预测,采用NSGA-II进行机器寻优,生成满足限定目标的备选维修方案集,为管养决策的优化提供参考。
1 网级状态评估与管养策略优化框架
区域内的多源信息和桥梁结构性能存在一定的关联性和延续性。具体而言,属于同一交通路网的桥梁群体在相似的环境因素(车流量、温湿度等)作用下,总是倾向于呈现类似的结构退化模式;此外,同一路段采用的桥梁设计规范和施工水平、质量也往往趋同[9]。基于此,本文提出图1所示的总体技术框架。该框架由数据集成模块、退化预测模块和管养决策模块组成。
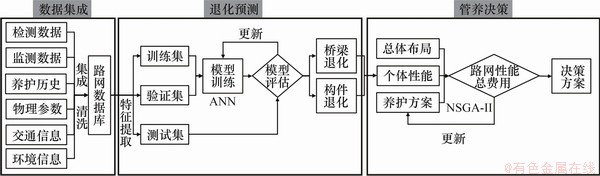
图1 网级评估与管养策略优化框架
Fig.1 Framework of network-level assessment and maintenance strategy
数据集成模块主要完成区域内桥梁状态数据的集成和清洗,形成合理有效的数据库。数据库的可靠性将直接决定后续分析的准确性和有效性。虽然原始数据经清洗和规整后,质量会有明显提升,但大部分数据仍存在难以消除的主观误差或噪声。
在退化预测模块中,主要进行特征提炼和退化模型训练,以完成对区域桥梁未来状态的精准预测。将数据库中筛选提取样本状态的主要特征,采用人工神经网络建立、训练、优化适用于桥梁结构及其组成部位的退化模型。退化模型作为桥梁退化规律的具现形式,提供了预测桥梁未来性能的有效手段。鉴于维修行为对结构性能有显著影响,本文提出将样本的维修历史作为影响因子之一,以精确模拟模型在不同维修方案下结构性能的变化。在管养决策模块中,基于退化模型生成的未来桥梁状态,结合区域总体桥梁布局和预设的管养目标,开展管养决策层面的优化分析。在指定路网场景中,考虑总维修成本、桥梁结构性能和路网安全状态等多目标函数,采用NSGA-II遗传算法进行机器寻优,生成特定约束条件下的帕累托最优解集,以指导实践工作和提升桥梁网级管理水平。优化的管养方案克服了现有被动管养策略的不足,可为不同目标提供各自最优桥梁管养方案。
2 针对桥梁状态退化模型的神经网络
2.1 退化模型的表达
在退化模型中,一般认为结构状态的量度与一系列自变量之间存在某种联系或规律。具体而言,该模型可表达为
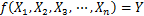 (1)
(1)
式中:结构状态的量度Y为考虑结构损伤程度的量化评估参数,可采用技术状况进行表征;而各类自变量Xn反映影响结构退化且具有可观测性的属性,如桥龄、桥梁跨径、车流量等。
已集成多源信息的路网数据库为桥梁退化特征的提取和建模提供了数据基础,但构建1个可以挖掘海量数据中参数内在联系的模型仍是核心问题。由于传统方法(确定性模型/随机性模型)存在局限性,而ANN对复杂逻辑运算和非线性关系具有较强的刻画能力,本文基于该算法建立区域桥梁的退化模型,通过选择合理的样本属性和对数据样本的合理训练,最终获得较高的预测准确率和置信度。
神经网络属于机器学习方法,主要由神经元、连接与权重、激活函数与阈值3部分构成。网络由众多基本计算单元(M-P神经元,图2)组成,单个神经元可连接n个输入参数和m个输出参数,且不同连接存在不同权重。神经元接收到总输入值后,由激活函数计算相应输出参数,并与设定阈值比对进行参数调整。其中,常用激活函数有Sigmoid,Tanh和ReLU等。
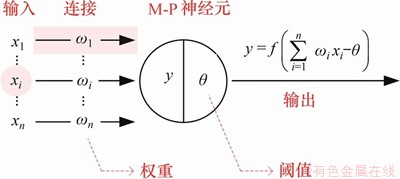
图2 M-P神经元
Fig.2 M-P neuron
2.2 网络架构与特征选择
当上一层神经元与下一层各神经元全互连时,即形成全连接神经网络。网络中除第一层(输入层)和最后一层(输出层)外,中间层(隐层)主要完成信号的加工与运算工作,网络架构如图3所示。为合理确定神经网络内各神经元的参数,采用误差逆传播(BP)算法进行计算。该算法可根据结果的反馈逐层前传,各神经元沿负梯度方向调整权重。为提高网络精度,可采用增加隐层数或/和增加神经元个数等来完成[17],但最合理的网络架构需经过模型比较来确定。
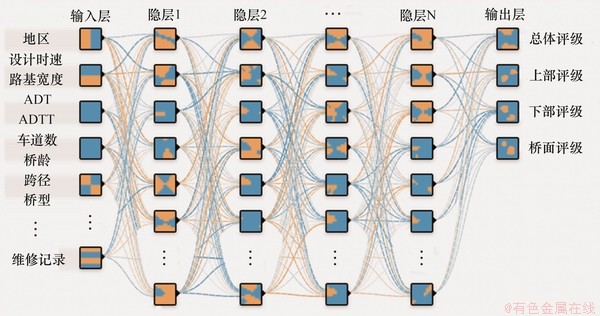
图3 神经网络的架构
Fig. 3 Structure of artificial neural network
经过数据预处理得到合适的特征子集(输入集)是另一个核心问题。过小的子集无法充分体现特征间的相关性,而过大的子集会因无关特征的加入使计算时间大幅度增加,甚至导致计算无法收敛。理论上,遍历属性集的任意组合并对比得出最优特征子集是最可靠的方法,但在计算上显然不可行。
为此,本文提出综合主观知识和客观统计的准则以确定特征子集。在第一步基于知识的准则中,借助领域知识、专家判断和工程经验等手段初选特征。本文根据对桥梁退化的主观认识及相关文献调研[10, 13],初步选取了可能的特征组合。在第二步基于统计的准则中,利用统计工具如频率统计、相关分析等对主观判断形成的子集进一步优化调整。最终形成的特征子集为地区、设计时速、路基宽度、平均日交通量(ADT)、年平均日货车交通量(ADTT)、车道数、桥龄、桥长、桥型、跨径及各部位维修记录。相应地,输出设置为总体评级、上部评级、下部评级和桥面评级。
3 基于NSGA-II的网级管养策略优化
3.1 NSGA-II算法寻优
遗传算法是一种模拟生物进化和自然选择方式来寻找最优解的算法。该算法中,每个染色体对应一个可行解,选用合适的适应度以评价解的好坏。种群中包含多组染色体,通过繁衍和进化更新种群世代以寻找到最优解集。在遗传算法中,NSGA-Ⅱ算法[16, 18]是带有精英保留策略的快速非支配多目标优化算法,对于多目标优化问题可以给出一组满足条件的最优解集(帕累托解集),其具有运行速度快、解集的收敛性好等优点。NSGA-Ⅱ算法与第一代相比有以下提升:引入快速非支配排序算法,在降低计算复杂度的同时将父代种群与子代种群进行融合,使下一代种群可以从双倍空间中选取保留所有最优秀的个体;引入精英策略,降低了优秀种群个体在进化时被丢弃的概率,从而提高了计算精度;引入拥挤度和拥挤度比较算子,不但克服了第一代算法中需人工干预的缺陷,并且将种群中的个体比较均匀地扩展到整个Pareto域,从而保证了种群多样性。
本文基于NSGA-Ⅱ算法提出了针对路网管养策略优化框架(图4)。本问题中,染色体为该路网可用的维修方案,即维修作用的桥梁对象和时间节点。在多目标优化中,为实现维修方案在多个维度上的权衡,本文设立2个目标函数:函数1为路网总体状态的安全指标;函数2为路网管养投入的费用指标。
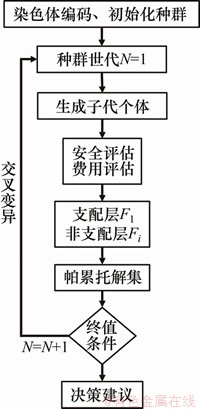
图4 路网管养策略的NSGA-II寻优方法
Fig.4 NSGA-II optimization for road network maintenance strategy
具体而言,针对某备选方案P,若种群中方案Q的2个目标均比方案P的好,则称Q支配P,且称P为支配解,反之P是非支配解。遍历整个种群,将所有支配解划入支配层F1,非支配解分别划入非支配层Fi(i=2,3,…,N-1)中,其中i为该非支配解被支配次数。引入拥挤距离以保证种群多样性,使染色体能在解的空间内均匀分布。对于同一支配层内个体j,按下式计算其与相邻2个体j-1和j+1的拥挤距离Dj:
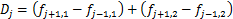 (2)
(2)
式中: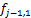 为第j-1个个体经目标函数1计算后所得的结果,其他类似。综合支配层和拥挤距离可实现多目标下的适应度排序,世代进化后得到最优解集,称为帕累托前沿(Pareto front)[19]。算法寻优后得到的最优解集中,每个解都是在各自条件下的相对最优,均不具备相互替代的作用。
为第j-1个个体经目标函数1计算后所得的结果,其他类似。综合支配层和拥挤距离可实现多目标下的适应度排序,世代进化后得到最优解集,称为帕累托前沿(Pareto front)[19]。算法寻优后得到的最优解集中,每个解都是在各自条件下的相对最优,均不具备相互替代的作用。
3.2 安全与费用指标
对于目标函数中的桥梁路网安全指标,根据KIM等的研究[11],路网的退化速率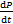 可按:
可按:
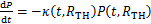 (3)
(3)
式中: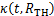 为退化因子;
为退化因子;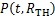 为路网在第
为路网在第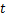 年的总体性能表达式,其本质为区域内任意桥梁的总体评级超过阈值
年的总体性能表达式,其本质为区域内任意桥梁的总体评级超过阈值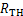 的概率,即
的概率,即
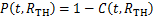 (4)
(4)
式中: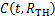 为第
为第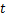 年区域内桥梁评级的累积分布函数在
年区域内桥梁评级的累积分布函数在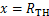 时的取值。
时的取值。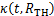 又可表达为
又可表达为
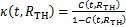 (5)
(5)
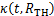 综合了退化过程的时变特性和统计分布特征,能够较好地表征目标路网在给定时刻的安全储备,且随着数值的增加,路网逐渐趋近于不安全。因此,本文建议采用
综合了退化过程的时变特性和统计分布特征,能够较好地表征目标路网在给定时刻的安全储备,且随着数值的增加,路网逐渐趋近于不安全。因此,本文建议采用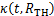 作为安全指标。
作为安全指标。
在桥梁路网的费用指标计算中,评估某一维修方案造成的总费用十分复杂。在全寿命理念中,不仅包括维修的直接成本和间接成本,而且需考虑全寿命周期内的运营成本[14, 20-21]。FABER等[20]提出,混凝土结构的全寿命成本由检测成本、维修成本、失效成本组成,且都受管养策略影响。而FRANGOPOL等[14]认为,桥梁结构的全寿命成本还应包括初始成本与例行维护成本。上述成本分量在寿命周期内随管养策略的变化使总费用更难预测,但鉴于准确的成本估算和费用计算并非本文重点,本文将费用指标简化为区域内所有桥梁维修次数,以粗略表征总体费用投入情况。
4 网级评估与管养策略优化在区域内的实现
4.1 样本筛选与数据处理
本文集成河北省内若干主线高速公路的多源数据(桥梁历史检测报告、监测评估报告、设计图纸等)得到河北省路网数据库。根据筛选出的特征类别和图3所示的网络结构,从路网数据库中筛选并生成神经网络训练所需的样本。综合考虑数据的完整性和时间的连续性,排除异常数值的部分记录,共得到由1 362座桥梁组成的7 225组总体样本,使本文训练得到的退化模型具有较强的泛化能力(可表达桥梁退化普遍规律),且不出现“欠拟合”或“过拟合”现象,将样本数据随机划分为训练集(80%)、验证集(10%)和测试集(10%)。训练集通过使预测误差最小化调整神经网络内各神经元之间的权重;验证集用来确定最优权重;测试集用来估计神经网络的桥梁退化评估效果。
本文输入变量具有多种数据类型,包括数值型(如桥龄、ADT)、标称型(如地区、桥型)、布尔型(如维修记录)。对于各类输入变量需进行二次编码以适应神经网络的训练,见表1。
表1 神经网络的输入与输出
Table 1 Input and output of neural network
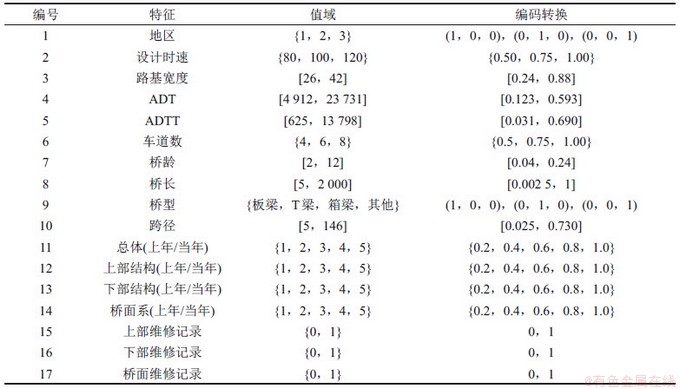
对于数值型特征,由于特征值域相差较大易导致值域窄的特征出现特征稀释现象,本文利用最小-最大规范化法(min-max normalization)将所有特征值映射到[0,1]区间上,按
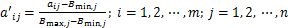 (6)
(6)
式中: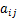 为第
为第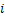 个样本的第
个样本的第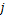 个原始特征对应的变量;
个原始特征对应的变量;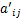 为规范化处理后对应的变量;
为规范化处理后对应的变量;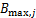 为特征
为特征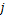 的上界取值;
的上界取值;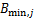 为特征
为特征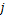 的下界取值。
的下界取值。
对于标称型,按独热编码(one-hot encoding)处理为1×N的向量,其中N为类别数。以地区为例,在路网数据库中预设的值域为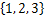 ,则可分别编码为
,则可分别编码为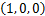 ,
,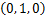 ,
,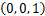 ,且分别对应3个输入神经元。特别地,布尔型包含本文所提出的新增特征维修记录,代表该部位在上一年是否存在维修,输入时以1(有维修)或0(未维修)表示。
,且分别对应3个输入神经元。特别地,布尔型包含本文所提出的新增特征维修记录,代表该部位在上一年是否存在维修,输入时以1(有维修)或0(未维修)表示。
本文建立的神经网络输出采用结构的评级,原因在于:评分数据(数值型)变异性过大,易导致模型精度降低。参考公路桥梁技术状况评定[22]及维归约思想,将[80,100]的总体评分区间重新划分为5个状况级别:
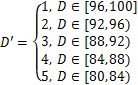 (7)
(7)
式中: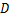 为原始总体评分;
为原始总体评分;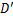 为对应总体评级。此转换可保证结构技术状况不变。
为对应总体评级。此转换可保证结构技术状况不变。
转换后的结构评级在神经网络中如何表达,不同研究者对此看法不一。MORCOUS[10]认为,桥梁结构或构件的MCR(material condition rating)虽是用序数等级进行标度的,但实际上是通过多个子结构的MCR加权得到,因此建议按数值型使用。与之相反,HUANG[23]倾向于将结构评级视为标称型,按独热编码向量化处理;李龙祥等[12]的观点与之类似。事实上,这代表研究者对学习任务的不同定义,即神经网络是一个分类器还是一个回归器。考虑到本文所使用的结构评级虽具有一定的类别含义,但其更侧重于用数值表征结构的变化,故将其作为数值特征处理。相应地,本文将神经网络定义为一个回归器。
4.2 不平衡数据的代价敏感误差
由于本文的总体样本数据分布具有显著的不平衡性,即大部分样本的结构评级集中在式(3)定义的1~3级,而4~5级桥梁占比不足10%。该不平衡特性易导致神经网络在训练过程中对高评级样本过拟合,而对低评级样本欠拟合。若不在误差模型中加权处理,此类神经网络易引起桥梁管理的安全隐患,即将一个存在明显缺陷的桥梁判断为高评级桥梁而错失维修时机造成期望外的损失甚至重大事故。为降低此类“非均等代价”,充分考虑各类评级的相对重要性,本文选用代价敏感型训练误差以评估模型的精准性[24],即
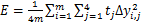 (8)
(8)
式中:E为模型预测的最终误差;m为样本数量;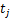 为输出层第j个分量对应的代价参数;
为输出层第j个分量对应的代价参数;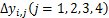 为样本i在输出j上与真值的偏差。由于输出层有4个神经元,故进行加权处理。
为样本i在输出j上与真值的偏差。由于输出层有4个神经元,故进行加权处理。
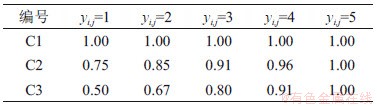
本文在确定各类代价的权重时,先设定不同代价系数,再通过验证集的对比和调整,确定最适宜的代价系数。本文设立的各类代价取值如表2所示(yi,j=1,代表评级为1时的输出),其中,C1为均等代价情况,而C2和C3中低评级样本的代价逐渐提高。
表2 tj(j=1,2,3,4)的取值
Table 2 Values of tj(j=1, 2, 3, 4)
4.3 模型的训练与评估
模型内除了代价参数需要确定外,还需确定隐层的数量。本文对比考虑3种隐层数量(2,3和4层),结合3类代价取值,共产生3×3=9个候选神经网络。各模型在训练时的误差-迭代曲线如图5所示。
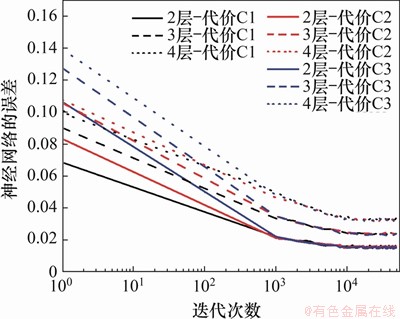
图5 各类模型的误差-迭代曲线
Fig. 5 Error-iteration curves of each models
在图5中,黑线、红线和蓝线分别代表代价C1,C2和C3代价组合;实线、虚线和点线分别代表2,3和4层神经网络。所有神经网络的误差(训练结果与真值的差值)在训练初期均表现出快速下降并最终达到稳定,但对比代价C1,C2和C3,各模型收敛时机虽保持一致,但初始误差依次增大,而收敛速度亦加快。并且隐层数的增加也会加快模型的收敛速度。为比较候选模型的预测性能差异,进一步在验证集上选取准确率(A)统一衡量,定义如下:
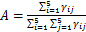 (9)
(9)
式中:γij为属于第i类的样本被预测为第j类的数目。
每个模型的4个输出特征对应的A见图6。由图6可见:C1模型的A上比C2和C3模型的A稍低,且隐层数量增多,预测结果更好。综合比较9个候选模型,认为模型(隐层=4,C2)最稳定、可靠,表3也表明该模型具有良好的泛化性能。
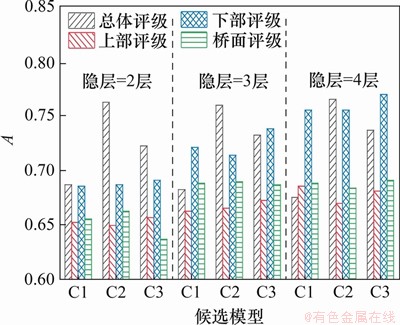
图6 候选模型总体/部位评级A
Fig. 6 Accuracy of candidate rating models
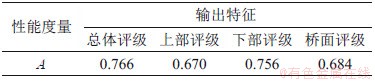
表3 模型(隐层=4,C2)的泛化性能测试
Table 3 Generalization performance testing of model(hidden layer=4, C2)
4.4 桥梁管养策略分析
由于路网安全状态与路网内的各个桥梁的状态密切相关,桥梁的退化程度不同会明显影响路网的安全状态,且维修时机不同也同样会影响桥梁最终的状态,为此,本节将量化显示维修方案对桥梁状态的影响。
利用本文已得到的最优模型(隐层为4层,C2),共设定3种对比方案,其中方案A为无任何维修,方案B为在第4年及第7年对全桥进行维修,方案C为在第5年对全桥进行维修。图7给出了各模型关于总体评级的预测结果。由图7可见:在方案A中,未来10 a该桥梁总体评级将从1退化至4;方案B中,由于维修的改善作用,10 a后仅退化至评级2;方案C中仅发生1次维修,故维修的改善作用较小,10 a后将退化至评级3。由此可见,具体的维修行为对桥梁的退化过程有着重要影响,然而,维修方案的差异同样会造成总费用发生变化。在区域内,路网桥梁数目众多,为平衡总费用和路网状态的关系并满足相应初始条件,区域桥梁的网级管养方案决策可以转化为1个优化问题,并通过数值算法进行求解。
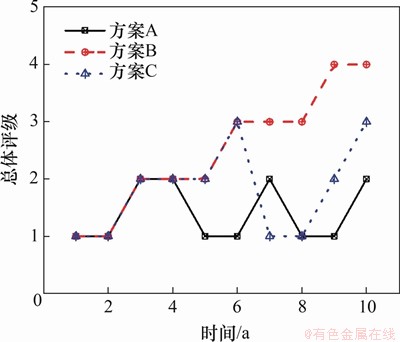
图7 基于网级评估的维修方案控制
Fig. 7 Maintenance scheme using network-level assessment
4.5 网级管养策略的优化
本节选用河北省邢临高速的某主干路段内的小型路网进行管养策略优化分析,其中包含50座公路桥梁。基于本文提出的NSGA-II遗传算法,设定染色体x是一个50×3维矩阵,其中每个分量xit(t=1,…,50;t=1,2,3)存放1个1×3维的二值向量,代表第i座桥梁在第t年采取的具体维修行为。例如,[1,1,0]表示该桥在这一年中将对上部结构和下部结构进行维修,而桥面系不采取相应措施。同时,设定种群数为1 000(即每代种群包含1 000个最优染色体),设定世代数为1 000(种群的选择和进化过程将迭代1 000次),设定交换概率为90%,突变概率为10%。根据本文分别定义2个目标函数,即
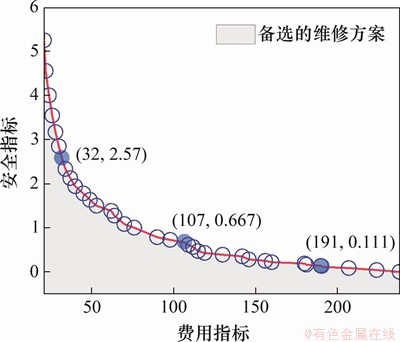
图8 未来3 a的备选维修方案集
Fig. 8 Maintenance scheme set for the next 3 years
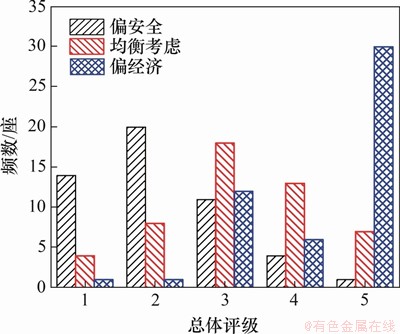
图9 3个方案的管养效果对比
Fig. 9 Comparison on maintenance effects of three schemes
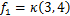 (10)
(10)
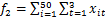 (11)
(11)
式中:f1与f2分别为前述安全指标与费用指标,且t=3,RTH=4。则所求解问题可进一步表述为
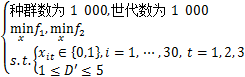 (12)
(12)
图8所示为求解给出的未来3 a该路网的备选维修方案集,图中每个点代表符合给定约束条件的1种可行解,且各自均具有相对优势。图8中左上方的经济偏好可行解(32,2.57)、位于中部的均衡方案(107,0.667)和右下方安全偏好可行解(191,0.111)的最终效果如图9所示。由图9可知:相比之下,“经济偏好中”要求更少的经费投入,在此管养方案下路网的桥梁状态评分会偏低,且桥梁总体评级分布呈现双峰形态,即状态劣化的桥梁维修较少,而状态良好的桥梁改善效果与保持状态良好,虽然其符合问题中的限定约束和目标函数,但不太适合实际应用;而“安全偏好中”则呈现单峰形态,且向评级2以上聚集,状态保持良好的桥梁明显增多,但所消耗的总经费亦是所有备选方案中最高的。在均衡方案中,分布呈现单峰形态且在评级3左右聚集,状态极好或极差的桥梁均较少。由此可见,此算法可以为桥梁管理者提供满足需求的多种方案,实际选取中可根据工程需求、区域差异、工作侧重点等方面,从备选方案中选取最适合方案。
5 结论
1) 利用人工神经网络构建了区域内桥梁状态与各特征属性之间的关系,建立了桥梁状态退化模型,并泛化至时间维度实现了桥梁和构件的状态预测。综合主观知识和客观统计信息,从集成的路网数据库中提炼出表征桥梁状态的特征子集作为神经网络的可靠输入。针对各特征属性的数据类型,建立了各自的二次编码规则以适应神经网络的训练。由于区域内桥梁结构状态的分布不均匀,神经网络内选用代价敏感型训练误差以提高模型的预测精度。
2) 采用带精英策略的非支配排序遗传算法,结合路网安全和费用指标,实现了路网级桥梁管养策略的机器寻优。算法借助模拟生物进化和自然选择的方式,选取合适的评价适应度,寻找得到符合目标函数和限定条件的最优路网桥梁管养策略解集。安全指标考虑了桥梁退化的时变特性和统计分布特征,用于表征目标路网在给定时刻的安全储备。
3) 借助集成河北省若干高速公路多源数据的路网数据库,训练并验证了基于人工神经网络的省内高速公路桥梁退化模型。在模型比选中,综合模型的收敛特性和预测准确率,确定了神经网络的最优架构层数和代价敏感型训练误差的权重。通过控制各部位维修记录的输入,借助建立好的退化模型实现了对单体桥梁在不同维修策略下状态变化的动态预测,量化了维修方案对单体桥梁状态的影响。
4) 以河北省内小型路网为例进行管养策略优化分析,结合本文提出的非支配排序遗传算法及路网安全和费用指标,为桥梁管理者提供了满足多设定需求的管养方案集。每个方案都具有各自的相对优势,例如经济偏好方案、安全偏好方案,及均衡考虑方案。经济偏好方案中经费投入少,但路网状态也会适当降低;安全偏好方案中桥梁状态极好,但总经费偏高;在均衡方案中,桥梁状态良好且经费投入适中。管理者可以根据实际需求从中选择最优者作为决策参考。
参考文献:
[1] 夏烨, 王鹏, 孙利民. 基于多源信息的桥梁网级评估方法[J]. 同济大学学报(自然科学版), 2019, 47(11): 1574-1584.
XIA Ye, WANG Peng, SUN Limin. A condition assessment method for bridges at network level based on multi-source information[J]. Journal of Tongji University(Natural Science), 2019, 47(11): 1574-1584.
[2] 孙利民, 尚志强, 夏烨. 大数据背景下的桥梁结构健康监测研究现状与展望[J]. 中国公路学报, 2019, 32(11): 1-20.
SUN Limin, SHANG Zhiqiang, XIA Ye. Development and prospect of bridge structural health monitoring in the context of big data[J]. China Journal of Highway and Transport, 2019, 32(11): 1-20.
[3] XIA Ye, WANG Peng, SUN Limin. Neutral axis-based health monitoring and condition assessment techniques for concrete box girder bridges[J]. International Journal of Structural Stability and Dynamics, 2019, 19(1): 1940015.
[4] 宗周红, 钟儒勉, 郑沛娟, 等. 基于健康监测的桥梁结构损伤预后和安全预后研究进展及挑战[J]. 中国公路学报, 2014, 27(12): 46-57.
ZONG Zhouhong, ZHONG Rumian, ZHENG Peijuan, et al. Damage and safety prognosis of bridge structures based on structural health monitoring: progress and challenges[J]. China Journal of Highway and Transport, 2014, 27(12): 46-57.
[5] 聂功武, 孙利民. 桥梁养护巡检与健康监测系统信息的融合[J]. 上海交通大学学报, 2011, 45(S1): 104-108.
NIE Gongwu, SUN Limin. Integration of inspection and structural health monitoring system for bridge management[J]. Journal of Shanghai Jiao Tong University, 2011, 45(S1): 104-108.
[6] 黄侨, 任远, 许翔, 等. 大跨径缆索承重桥梁状态评估的研究现状与发展[J]. 哈尔滨工业大学学报, 2017, 49(9): 1-9.
HUANG Qiao, REN Yuan, XU Xiang, et al. Research progress of condition evaluation for large span cable supported bridges[J]. Journal of Harbin Institute of Technology, 2017, 49(9): 1-9.
[7] 贺拴海, 赵祥模, 马建, 等. 公路桥梁检测及评价技术综述[J]. 中国公路学报, 2017, 30(11): 63-80.
HE Shuanhai, ZHAO Xiangmo, MA Jian, et al. Review of highway bridge inspection and condition assessment[J]. China Journal of Highway and Transport, 2017, 30(11): 63-80.
[8] 梁鹏, 王秀兰, 楼灿洪, 等. 基于裂缝特征库的混凝土梁桥承载能力快速评定[J]. 中国公路学报, 2014, 27(8): 32-41.
LIANG Peng, WANG Xiulan, LOU Canhong, et al. Rapid evaluation of load-bearing capacity of concrete beam bridge based on crack feature library[J]. China Journal of Highway and Transport, 2014, 27(8): 32-41.
[9] BOCCHINI P, FRANGOPOL D M. A probabilistic computational framework for bridge network optimal maintenance scheduling[J]. Reliability Engineering & System Safety, 2011, 96(2): 332-349.
[10] MORCOUS G. Performance prediction of bridge deck systems using Markov chains[J]. Journal of Performance of Constructed Facilities, 2006, 20(2): 146-155.
[11] KIM J I, KIM D K, FENG M Q, et al. Application of neural networks for estimation of concrete strength[J]. Journal of Materials in Civil Engineering, 2004, 16(3): 257-264.
[12] 李龙祥, 周凌宇, 黄戡, 等. 循环荷载下无砟轨道-桥梁结构体系刚度退化性能[J]. 中南大学学报(自然科学版), 2019, 50(10): 2481-2490.
LI Longxiang, ZHOU Lingyu, HUANG Kan, et al. Performance of stiffness degradation of structure system in ballastless track-bridge under cyclic load[J]. Journal of Central South University(Science and Technology), 2019, 50(10): 2481-2490.
[13] ALIPOUR M, HARRIS D K, BARNES L E, et al. Load-capacity rating of bridge populations through machine learning: application of decision trees and random forests[J]. Journal of Bridge Engineering, 2017, 22(10): 04017076.
[14] FRANGOPOL D M, DONG You, SABATINO S. Bridge life-cycle performance and cost: analysis, prediction, optimisation and decision-making[J]. Structure and Infrastructure Engineering, 2017, 13(10): 1239-1257.
[15] FRANGOPOL D M, LIU M. Bridge network maintenance optimization using stochastic dynamic programming[J]. Journal of Structural Engineering, 2007, 133(12): 1772-1782.
[16] 王晓明, 贺耀北, 李瑜, 等. 基于并行NSGA-Ⅱ算法的桥梁网络养护策略优化[J]. 土木工程学报, 2012, 45(1): 86-91.
WANG Xiaoming, HE Yaobei, LI Yu, et al. Optimization of maintenance strategy for bridge networks using parallel NSGA-Ⅱ algorithm[J]. China Civil Engineering Journal, 2012, 45(1): 86-91.
[17] 李惠, 鲍跃全, 李顺龙, 等. 结构健康监测数据科学与工程[J]. 工程力学, 2015, 32(8): 1-7.
LI Hui, BAO Yuequan, LI Shunlong, et al. Data science and engineering for structural health monitoring[J]. Engineering Mechanics, 2015, 32(8): 1-7.
[18] 夏烨, 雷晓鸣, 王鹏, 等. 针对网级评估的区域桥梁信息集成与数据挖掘[J]. 哈尔滨工业大学学报, 2020, 53(3): 66-74.
XIA Ye, LEI Xiaoming, WANG Peng, et al. Regional bridge information integration and data mining for network-level assessment[J]. Journal of Harbin Institute of Technology, 2020, 53(3): 66-74.
[19] 李爱群, 丁幼亮, 王浩, 等. 桥梁健康监测海量数据分析与评估: “结构健康监测”研究进展[J]. 中国科学: 技术科学, 2012, 42(8): 972-984.
LI Aiqun, DING Youliang, WANG Hao, et al. Analysis and assessment of bridge health monitoring mass data-progress in research/development of "Structural Health Monitoring"[J]. Scientia Sinica(Technologica), 2012, 42(8): 972-984.
[20] FABER M H, MIRAGLIA S, QIN Jianjun, et al. Bridging resilience and sustainability-decision analysis for design and management of infrastructure systems[J]. Sustainable and Resilient Infrastructure, 2020, 5(1/2): 102-124.
[21] 夏烨, 王鹏, 雷伟, 等. 基于中性轴的混凝土梁桥监测方法与指标研究[J]. 华南理工大学学报(自然科学版), 2019, 47(12): 62-71.
XIA Ye, WANG Peng, LEI Wei, et al. Neutral axis position-based monitoring method and indicator for structural evaluation of concrete girder bridges[J]. Journal of South China University of Technology(Natural Science Edition), 2019, 47(12): 62-71.
[22] 鲍跃全, 李惠. 人工智能时代的土木工程[J]. 土木工程学报, 2019, 52(5): 1-11.
BAO Yuequan, LI Hui. Artificial intelligence for civil engineering[J]. China Civil Engineering Journal, 2019, 52(5): 1-11.
[23] HUANG Yinghua. Artificial neural network model of bridge deterioration[J]. Journal of Performance of Constructed Facilities, 2010, 24(6): 597-602.
[24] 吴雨茜, 王俊丽, 杨丽, 等. 代价敏感深度学习方法研究综述[J]. 计算机科学, 2019, 46(5): 1-12.
WU Yuxi, WANG Junli, YANG Li, et al. Survey on cost-sensitive deep learning methods[J]. Computer Science, 2019, 46(5): 1-12.
(编辑 刘锦伟)
收稿日期: 2020 -07 -13; 修回日期: 2020 -08 -20
基金项目(Foundation item):国家重点研发计划项目(2019YFB1600702);国家自然科学基金资助项目(51978508);上海市科学技术委员会资助项目(19DZ1203004) (Project(2019YFB1600702) supported by the National Key Research and Development Program of China; Project(51978508) supported by the National Natural Science Foundation of China; Project(19DZ1203004) supported by the Science and Technology Commission of Shanghai Municipality)
通信作者:孙利民,博士,教授,从事桥梁健康监测、桥梁振动控制、桥梁抗震研究; E-mail: lmsun@tongji.edu.cn
引用格式: 夏烨, 雷晓鸣, 王鹏, 等. 针对网级评估的区域桥梁退化建模与演绎应用[J]. 中南大学学报(自然科学版), 2021, 52(3): 828-838.
Citation: XIA Ye, LEI Xiaoming, WANG Peng, et al. Degradation modeling and application of regional bridges for network-level assessment[J]. Journal of Central South University(Science and Technology), 2021, 52(3): 828-838.