Trans. Nonferrous Met. Soc. China 22(2012) 1738-1743

FEM analysis of workpiece curvature influence on groove deformation during plough process

LU Long-sheng, LIU Xiao-chen, TANG Yong, YUAN Dong

Key Laboratory of Advanced Manufacturing Technology of Surface Functional Structure of

Guangdong Higher Education Institutes, South China University of Technology, Guangzhou 510640, China

Received 13 September 2011; accepted 29 April 2012

Abstract: To investigate the workpiece curvature influence on groove deformation, numerical studies with curvature varying from negative to positive were conducted on copper material. Groove deformations were analyzed, including groove geometry, effective stress distribution and plough force. The curled groove shape whose workpiece curvature was 0.133 mm^-1 was validated by experiments. Moreover, a series of geometry models with various curvatures were introduced to analyze the change of groove deformation. The results show that positive curvatures influence groove deformation more intensively than negative or zero curvature. It is mainly due to the action of the tool forming face during plough process.

Key words: plough; workpiece curvature; microgroove; microchannel; finite element method

1 Introduction

Microchannels whose dimensions are in micrometer scale are always used for enhancing heat and mass transfer in electronic, chemical and cryogenic industries [1]. LIU et al [2] investigated the effect of microstructure on heat transfer capability of microchannels. Compared with ridge-shaped groove, shield-shaped groove, straight slot groove and plain surface, the V-shaped grooved microchannel possessed the highest heat transfer capability. Therefore, the manufacturing technology of V-shaped grooved microchannel attracts lots of researchers’ attention.

Plough is a chipless metal cutting technology to fabricate V-shaped grooved microchannel on copper materials. Since invented by TANG et al [3], plough technology has been applied in finned tube or grooved plate/sheet production for chemical, mechanical, electronic and photovoltaic industries. Different from the previous microchannel manufacturing technologies, such as molding replication [4] and electroforming [5], TANG et al [6] reported that the V-shaped grooves by plough possessed a tiny layer occupied by minor grooves, which was very useful to enhance heat and mass transfer [7]. Hence, the plough technology needs to be studied.

Generally, workpiece curvature is an important factor that influences the formation of metal cutting technologies. For machining workpiece with variable curvatures, the cutting condition is process-dependent [8]. Compared with the straight surfaces machining, machining the curved surfaces is variable in feed direction, actual cutting federate and cutter engagement [9]. DESAI and RAO [10] found that the variations of workpiece geometries resulted in variable cutting forces and surface errors during machining curved geometries. Furthermore, compared with convex geometries, the effect of cutter diameter was predominant in concave geometries. RAO et al [11] investigated the peripheral milling process for variable curvature surfaces. They found that significant errors in calculation of machining parameters and cutting forces appeared while the variable workpiece curvature was instead by locally constant one. In another paper, RAO et al [12] reported that under identical cutting conditions, normal cutting forces increased from convex geometries to concave geometries, and straight surface (zero curvature) was in the middle of the two. BOUD [13] discovered that bar diameter which affected curvature had influence on tool temperature and tool wear. Therefore, to study a metal cutting technology, the influence of workpiece curvature on processing procedure is important.

Lots of studies about plough have been done, including groove formation mechanism [14], and optimal processing parameters [15], etc. However, the influence of workpiece curvature on the groove formation and process design has never been reported. Furthermore, most of the studies about plough technology were done with experimental method. Therefore, several numerical experiments with seven different curvatures during ploughing were carried out.

2 Experimental model and procedure

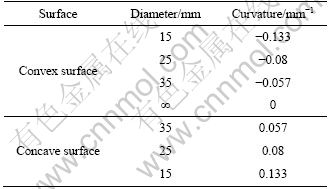
Experiments were conducted on copper material with seven different curvatures (ξ). To distinguish the curvature, the curvature of concave surface was defined as positive, the curvature of convex surface was defined as negative, and the curvature of flat surface was 0. The conversions between diameters and curvatures are illustrated in Table 1. The wall thickness and width of workpiece are 1 mm and 4 mm, respectively.

Table 1 Conversions between diameter and curvature

Numerical simulations were carried out by using DEFORM ver. 2001 with rigid-plastic principle. Figure 1 shows the schematic diagram of plough process under different surfaces, in which Z is the axial direction, R is the radial direction, and θ is the circumferential direction. The parameters of plough tool are: plough angle (γ_e) 30°, forming angle (β) 25°, plough clearance angel (α) 70°, inclination angle (λ_s) -40°. And the parameters of plough process are: plough depth (α_p) 0.4 mm, rotation speed 50 r/min.

To simplify the finite element method(FEM), the main motion was achieved by the movement of plough tool, while the workpiece was set to be statistic. To speed up the simulation process, the dimensions of workpiece were minimized. Due to its axisymmetric, the workpiece could be selected with any dimension which was large enough to steady the plough process. With the selected plough parameters, an 8 mm-length of arc or plate was enough for FEM studies.

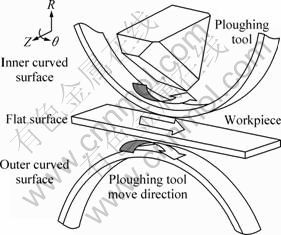
Fig. 1 Schematic diagram of plough process under different surfaces

During simulating process, the workpiece was set as plastic body, and the plough tool was set as rigid body because of its high hardness; the elastic modulus of copper was set as 115 GPa, Poisson ratio was set as 0.33, and coefficient of linear expansion was set as 1.7×10^-5 K^-1. Furthermore, a simplified friction model applied was F_s=μ[τ]A_f, where F_s is the frictional force, [τ] is the shear yield stress, μ=0.12 is the friction factor, and A_f is the contact area between tool and workpiece. Relative meshing technique was adopted. Furthermore, the other detailed FEM establishments were the same as those in Ref. [14].

3 Results and discussion

As a kind of microchannel, the performance of V-shaped groove is mainly affected by groove geometries, including groove width and depth. Furthermore, as a metal cutting technology, the effective stress distribution and cutting force are vital to analyze plough process.

3.1 Groove geometry analysis

Figure 2 shows the relationship between groove geometry and workpiece curvature during ploughing. While ξ<0, the groove depth and width are almost in  constant values. However, while ξ>0, the groove depth and width increase quickly, and the growth rates of both groove depth and width are speeded up as curvature increases. Besides, the growth rate of groove width is larger than that of groove depth. Especially, while the curvature overflows 0.08 mm^-1, the growth rate is speeded up quickly. Moreover, the zero curvature is the transformation point of the groove geometry change.

To investigate the reason of these phenomena, groove shape in cross section was observed, as shown in Fig. 3. The groove shape changes a little while ξ≤0, but it changes obviously while ξ>0. While ξ=0.133, groove width increases sharply and the groove appears to be in a totally different shape compared with others. It exhibits curled shape instead of triangular shape where normal groove exhibits. Therefore, a large growth rate of groove width occurs at this curvature.

Fig. 2 Influence of workpiece curvature on groove geometry dimensions

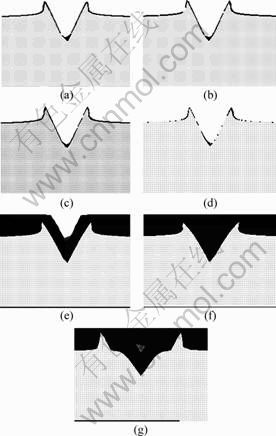
Fig. 3 Influence of workpiece curvature on groove shape:    (a) ξ=-0.133 mm^-1; (b) ξ=-0.08 mm^-1; (c) ξ=-0.057 mm^-1;  (d) ξ=0 mm^-1; (e) ξ=0.057 mm^-1; (f) ξ=0.08 mm^-1; (g) ξ=0.133 mm^-1

3.2 Effective stress distribution analysis

Because the tool rake face was symmetric, the effective stress analysis was done in two cross sections, which were cutting edge plane and main section plane on tool tip. Figures 4 and 5 show the effective stress distribution with different curvatures in cutting edge plane and main section plane, respectively.

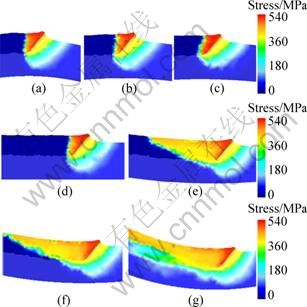
Fig. 4 Effective stress distribution of workpiece with different curvatures in cutting edge plane: (a) ξ=-0.133 mm^-1; (b) ξ= -0.08 mm^-1; (c) ξ=-0.057 mm^-1; (d) ξ=0 mm^-1; (e) ξ=0.057 mm^-1; (f) ξ=0.08 mm^-1; (g) ξ=0.133 mm^-1

At a certain curvature, the effective stress decreases with the metal far away from the tool rake face. However, the volume and location of the metal which is in stress state differ as curvature changes. As the same as groove shape, the zero curvature is the transformation point of the effective stress changes.

While ξ<0, the stress influence area differs a little except only a tiny decease of the depth in cutting edge plane. It locates nearby the interfaces between the tool rake face and workpiece. Besides, it also locates ahead of the minor cutting edge at the feed direction. While ξ=0, the shape of effective stress influence area is similar to that of ξ<0, but its volume is a little smaller than that of ξ<0.

While ξ>0, the effective stress influence area increases quickly. It extends to the entire tool forming face-workpiece interface at the groove wall. And its volume increases as the curvature increases. These indicate that the tool forming face plays an important role in groove deformation besides tool rake face. As ξ ranges from 0 to 0.08 mm^-1, the effective stress at groove bottom which faces the tool clearance face is nearly 0, which indicates that the tool clearance face does not contact workpiece at this moment. As ξ increases to 0.133 mm^-1, the stress influence area increases a lot. It is due to the metal at the groove bottom also in stress state. This indicates that the clearance face comes to compress the metal at this moment.

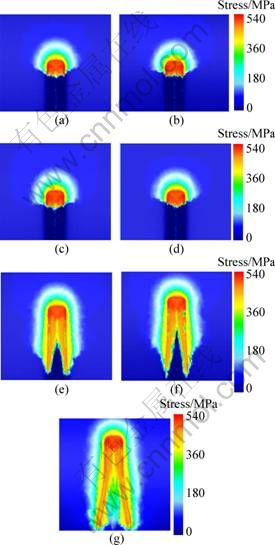
Fig. 5 Effective stress distribution of workpiece with different curvatures in main section plane: (a) ξ=-0.133 mm^-1; (b) ξ= -0.08 mm^-1; (c) ξ=-0.057 mm^-1; (d) ξ=0 mm^-1; (e) ξ=0.057 mm^-1; (f) ξ=0.08 mm^-1; (g) ξ=0.133 mm^-1

3.3 Plough force analysis

The plough forces at variable workpiece curvatures are shown in Fig. 6. While ξ<0, both radial plough force (F_R) and circumferential force (F_θ) increase very slowly, and F_θ is larger than F_R. While ξ>0, both radial plough force and circumferential force increase as curvature increases. Furthermore, the growth rate of F_R is larger than F_θ, which finally results in F_R larger than F_θ. Generally, the plough force of positive curvature is larger than that of negative one. These phenomena are consistent with the effective stress distribution very well. Therefore, the stiffness of the plough system should be carefully designed while plough on workpiece with positive curvature.

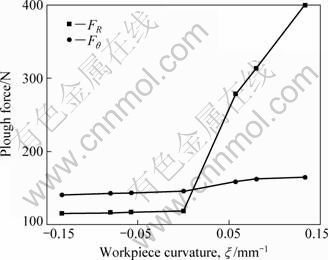
Fig. 6 Cutting force curves of workpiece with different curvatures during plough

3.4 Experimental validation

Numerical simulations indicate that the workpiece curvature in negative or zero range influences the groove deformation a little. However, the positive curvature will influence the groove deformation obviously, especially while ξ=0.133 mm^-1. Because the experimental results of groove deformation on workpiece with curvature less than 0.133 mm^-1 can be easily found in Refs. [3,6,14], to validate the numerical results, experiments were carried out only on workpiece with ξ=0.133 mm^-1. Figure 7 shows the groove image in cross section after ploughing. Compared with the grooves fabricated by ploughing reported before [3,6,14], the groove is curled on the top, just as predicted by the simulations. Furthermore, some copper materials are observed to adhere to the tool clearance face, which can be used as an evidence of the formation mechanism of the curled groove.

Fig. 7 Groove image as ξ=0.133 mm^-1 by plough method

3.5 Geometry analysis

To investigate the reason of the workpiece curvature influence on groove deformation, a series of geometry models with various curvatures were introduced, as shown in Fig. 8. They were presented in main section tool system, including reference plane (P_r), cutting edge plane (P_s) and main section plane (P_o). After feeding a plough depth (α_p), the plough tool compresses the original metal to form a bulge [3] ahead of the cutting edge area. Then the metal in bulge will be split off by the cutting edge and squeezed out by the tool rake face. While passed through the rake face, the groove shape will be further influenced by tool forming face. Finally, a groove is fabricated.

While ξ≤0, the influence of tool forming face on groove width is relatively small. For the contact surface between workpiece and tool forming face, which is illustrated as surface AJC, the maximum distance between groove top and main section plane (P_o) locates at the reference plane (P_r). Therefore, the groove width is equal to the width of tool forming face at point B, which means that the groove width will keep a constant value at a certain plough depth while ξ≤0. This can be used as an explanation that the groove shape changes little as the curvature changes. Furthermore, only a partial forming face, which is identified as surface AJB, takes part in the groove formation. Because the area of surface AJB increases slowly as curvature increases, the plough force increases slowly as curvature increases.

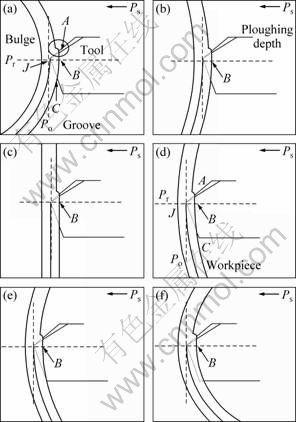
Fig. 8 Geometry model of plough process in cutting edge plane with different curvatures: (a) ξ=-0.133 mm^-1; (b) ξ=-0.057 mm^-1; (c) ξ=0 mm^-1; (d) ξ=0.057 mm^-1; (e) ξ=0.08 mm^-1;    (f) ξ=0.133 mm^-1

While ξ>0, the location of the maximum distance between groove top and main section plane (P_o) will migrate from point B to point C, which means that other partial surface JCB of tool forming face will compress the groove surface. Because the distance between groove top and main section plane (P_o) on surface JCB is larger than that in reference plane (P_r), and the groove dimensions will increase further. Furthermore, the area of surface JCB increases as curvature increases, which results in the increase of plough force. As ξ increases to 0.133 mm^-1, where tool clearance face totally immerges into groove, the tool clearance face will forge the groove curled. And an obvious increase of groove geometry and plough force will occur because of the extensive friction action between workpiece and tool. Generally, the plough parameters which result in curled groove generation should be avoided.

To sum up, positive curvatures influence the groove deformation more intensively than negative or zero ones. And the tool parameters and plough depth should be carefully selected while ploughing the workpiece with positive curvature.

Figure 9 shows a detailed geometry model of plough process on concave surface, in which J is the nose of plough tool; Δh is the height of plough bulge; r is the radius of workpiece curvature; H_IJ is the height of cutting edge; H_JK is the height of clearance face; line IJ is the cutting edge; surface IJM is the rake face; surface MJK is the forming face; line JK is the clearance face projected on cutting edge plane. As the curvature increases, the cross point (A) at cutting edge between workpiece and tool will migrate from point J toward point I. As a chipless cutting method, the point A should never pass through point I. Therefore, the radius of curvature (r=1/ξ) should be selected as:

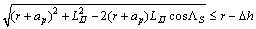     (1)

where L_IJ is the length of cutting edge, and it can be calculated as:

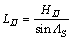                                (2)

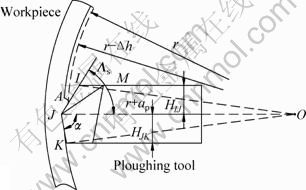
Fig. 9 Geometry model of plough process in cutting edge plane

Moreover, to avoid the clearance face compressing the grooves as the curvature increases, the clearance angle should be selected as:

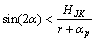                             (3)

4 Conclusions

1) Based on the analysis of groove geometry, effective stress distribution and plough force, the positive curvature of workpiece affects the groove deformation more intensively than negative or zero curvature ones.

2) The action of tool forming face results in the changes of groove deformation with different curvatures. For ploughing on workpiece with positive curvature, the increase of contact area between tool forming face and workpiece will result in the increases of groove geometry and plough force.

3) To avoid the generation of grooves with curled shape, the tool parameters and plough depth should be carefully selected while ploughing the workpiece with positive curvature.

References

[1] EDEL Z J, MUKHERJEE A. Experimental investigation of vapor bubble growth during flow boiling in a microchannel [J]. International Journal of Multiphase Flow, 2011, 37(10): 1257-1265.

[2] LIU Yang, CUI Jing, LI Wei-zhong, ZHANG Ning. Effect of surface microstructure on microchannel heat transfer performance [J]. Journal of Heat Transfer, 2011, 133(12): 124501.

[3] TANG Yong, ZHANG Fa-ying, CHEN Cheng-zhou, LUO De-wei. Study on the mechanism of extrusion-ploughing during manufacturing copper outside fin tube [J]. Tool Engineering, 1997, 31(1): 7-10. (in Chinese)

[4] MEI F H, PARIDA P R, JIANG J, MENG W J, EKKAD S V. Fabrication, assembly, and testing of Cu- and Al-based microchannel heat exchangers [J]. Journal of Microelectronic Systems, 2008, 17(4): 869-881.

[5] YU W, DESMULLIEZ M P Y, DRUFKE A, LEONARD M, DHARIWAL R S, FLYNN D, BOGN?R G, POPPE A, HORVATH G., KOHARI Z, RENCZ M. High-aspect ratiometal microchannel plates for microelectronic cooling application [J]. Journal of Micromechanics and Microengineering, 2010, 20(2): 25004-25011.

[6] TANG Yong, LU Long-sheng, PAN Min-qiang, LIU Xiao-kang, LIU Xiao-qing. Formation mechanism of external finned tubes by extrusion-plough method [J]. Transaction of Nonferrous Metals Society of China, 2006, 16(s1): s283-s288.

[7] WANG J L, CATTON I. Enhanced evaporation heat transfer in triangular grooves covered with a thin fine porous layer [J]. Applied Thermal Engineering, 2001, 21(17): 1721-1737.

[8] YANG Yun, ZHANG Wei-hong, WAN Min. Effect of cutter run out on process geometry and forces in peripheral milling of curved surfaces with variable curvature [J]. International Journal of Machine Tools & Manufacture, 2011, 51(5): 420-427.

[9] WEI Zhao-cheng, WANG Min-jie, MA Ri-guang, WANG Le. Modeling of process geometry in peripheral milling of curved surfaces [J]. Journal of Materials Processing Technology, 2010, 210(5): 799-806.

[10] DESAI K A, RAO P V M. Effect of direction of parameterization on cutting forces and surface error in machining curved geometries [J]. International Journal of Machine Tools & Manufacture, 2008, 48(2): 249-259.

[11] RAO V S, RAO P V M. Modelling of tooth trajectory and process geometry in peripheral milling of curved surfaces [J]. International Journal of Machine Tools & Manufacture, 2005, 45(6): 617-630.

[12] RAO V S, RAO P V M. Effect of workpiece curvature on cutting forces and surface error in peripheral milling [J]. Journal of Engineering Manufacture, 2006, 220(9): 1399-1407.

[13] BOUD F. Bar diameter as an influencing factor on temperature in turning [J]. International Journal of Machine Tools & Manufacture, 2007, 47(2): 223-228.

[14] LU Long-sheng, TANG Yong, YUAN Dong, DENG Da-xiang. Groove deformation analysis of a single plough on inner copper tube [J]. Journal of Materials Processing Technology, 2011, 211(11): 1669-1677.

[15] WAN Zhen-ping, TANG Yong. Production of integral serrated outside finned tube using a combined method of rolling and wedging/extruding [J]. International Journal of Machine Tools and Manufacture, 2010, 50(5): 487-490.

工件曲率对沟槽犁切成形影响的有限元研究

陆龙生，刘晓辰，汤 勇，袁 冬

华南理工大学 表面功能结构先进制造广东普通高校重点实验室，广州 510640

摘  要：为了研究工件曲率对犁切过程中沟槽成形的影响，以软件DEFORM为工具，利用有限元法分析不同曲率下犁切沟槽的成形过程。分别比较不同曲率条件下成形的沟槽几何尺寸、有效应力分布和犁切力。采用实验验证了曲率在0.133 mm^-1条件下卷曲沟槽的成形。此外，为了分析沟槽成形变化的原因，建立了不同曲率工件的犁切过程系列几何模型。相比于负曲率或平面，正曲率对沟槽成形的影响最为显著。这主要是由犁切刀成形面对沟槽成形过程的影响而造成的。

关键词：犁切；工件曲率；微沟槽；微通道；有限元法

(Edited by YANG Hua)

Foundation item: Project (U0834002) supported by the Key Program of NSFC-Guangdong Joint Funds of China; Project (51005079) supported by the National Natural Science Foundation of China; Project (20100172120001) supported by Specialized Research Fund for the Doctoral Program of Higher Education, China; Project (10451064101005146) supported by the Natural Science Foundation of Guangdong Province, China

Corresponding author: LU Long-sheng; Tel: +86-20-87114634; E-mail: meluls@scut.edu.cn

DOI: 10.1016/S1003-6326(11)61381-2