基于数值计算与遗传神经网络热熔钻研究

温继伟，陈晨

(1. 吉林大学 建设工程学院，吉林 长春，130026；

2. 吉林大学 超硬材料国家重点实验室，吉林 长春，130012；

3. 国土资源部复杂条件钻采技术重点实验室，吉林 长春，130026)

摘要：对热熔钻进过程中热熔体的相关问题展开研究，建立相应的数学模型，结合热熔钻进实验过程中的相关参数进行计算，得到了相应的解析解，并分析其规律与产生的原因，计算结果的变化规律与实际过程基本相符，表明所构建的数学模型是可靠的。此外，对热熔钻进过程中孔壁周围玻璃状硬壳的形成展开研究并给出了可靠的硬壳厚度计算的经验公式。将遗传算法与BP算法相融合构建GA-BP神经网络分别对有关热熔体与施加在热熔器上的有效热功率及钻压对热熔钻进速度的影响的数据进行预测。研究结果表明：基于GA-BP神经网络对热熔体在环空间隙中流速的分布，热熔体作用在热熔器外表面上的压力，热熔体作用在热熔器上的摩擦力，热熔器有效热功率在不同地层中对热熔钻进速度的影响和热熔器施加不同钻压在不同地层中对热熔速度影响的预测得到数据的均方误差比基于BP神经网络预测得到数据的均方误差分别小0.449×10^-6，0.005 6，0.001 1，0.104和0.136，且GA-BP网络比BP网络的计算时间分别短7，15， 2， 9，和15 s。

关键词：热熔钻；热熔体；玻璃状硬壳；数值计算；神经网络

中图分类号：TP183          文献标志码：A         文章编号：1672-7207(2013)12-5051-09

Study on hot melt drilling based on numerical computation and genetic neural network

WEN Jiwei, CHEN Chen

(1. College of Construction and Engineering, Jilin University, Changchun 130026, China;

2. State Key Laboratory of Superhard Materials, Jilin University, Changchun 130026, China;

3. The Key Laboratory of Complex Condition Drilling and Mining Technology of Ministry of Land and Resources, Changchun 130026, China)

Abstract: Through the study on the series of problems of hot melt in the drilling process, the mathematical models were established, and by calculating the relevant parameters in hot melt drilling experiment, the corresponding analytical solutions was obtained, and its own laws and the produced reasons was analysed, the variation of the calculation results were basically the same with the actual process. It is shown that the constructed mathematical model is reliable. In addition, the study on the glassy crust formation around the hole wall in the process of the hot melt drilling was conducted and the hard shell thickness calculated reliable empirical formula was given. Genetic algorithm and BP algorithm integration were used to build the GA-BP neural network to predict the data of the hot melt and the influence on hot melt drilling speed of the effective thermal power and the WOB applied to the subterrene. The results show that the mean square errors based on GA-BP neural network to predict the velocity distribution of hot melt in annular clearance, the role of the hot melt pressure on the outer surface of the subterrene, the friction of the hot melt in the subterrene, the influence on the hot melt drilling speed of the effective thermal power on the subterrene, the influence on the hot melt drilling speed of the impose different WOB on the subterrene in different stratas are 0.449×10^-6, 0.005 6, 0.001 1, 0.104, 0.136, respectively, which are lower than those based on BP neural network. And the computing time of GA-BP network are 7, 15, 2, 9 and 15 s, which are shorter than BP network.

Key words: hot melt drilling; hot melt; glassy hard shell; numerical calculation; neural network

热熔钻进是通过电加热器产生的集中于孔底的高温使井底及周围孔壁的岩土成分的团聚状态发生改变，导致其处于熔融状态，经过挤密或取心使钻孔延伸，同时冷凝后的热熔体还能在孔壁周围形成一层致密、高强度的玻璃状硬壳，完全可以取代套管进行护壁，随着热熔钻进地层深度的不断增加，地温逐渐升高，热熔钻进的效率也会相应地提高。热熔碎岩方法简单，附属设备及机具少，且不受岩石性质变化的限制，是一种前沿性的且极其富有前景的“广谱式”非常规碎岩新技术。热熔钻可应用于复杂地层地质勘探孔施工、水文水井施工、地热井施工、非开挖施工、冻土层勘探孔与天然气水合物勘探孔施工、石油勘探与开采井施工、盐井施工、土木工程施工(如：滑坡、露天矿与采石场的边坡加固、桩基孔施工等)、极地冰层钻探、超深科学钻探施工等领域^[1-6]。目前在国内热熔钻进方法尚处于实验室研究阶段，为了尽快将热熔钻推向实际生产应用中去，就需要对热熔钻进过程中的一系列相关问题展开研究，掌握热熔钻进碎岩的规律。本文作者在对热熔钻的研究中引入了遗传神经网络，将数值计算与人工神经网络相结合，综合运用这2种手段展开对热熔钻的研究。

1  热熔钻进实验

图1所示为热熔钻进实验台。热熔钻进实验时主要的配套设备有：钻机(低转速、能够加压到5~10 kN的钻机均可采用)；调压器(型号为TSGC2J-20，将高电压(380 V)调整为低电压(10 V))；整流器(型号为GDL-A，将交流电调整为直流电)。附属机具：热熔器、具有隔热环的特制钻杆。

理论分析及实验表明，热熔器外表面轮廓的最好形式为悬链线旋转体。若热熔器外表面的悬链线下部顶点距所钻进地层底面的距离为 a，热熔器的轴截面取决于其高度h和半径r，则热熔器的高度为：

图1  热熔钻进实验台

Fig. 1  Hot melt drilling experimental table

               (1)

热熔器外表面悬链线的剖面弧长为：

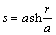                 (2)

热熔器工作面积为：

         (3)

     (4)

图2所示为热熔器外表面悬链线轮廓图。热熔器的横截面为圆形，纵向截面为悬链线旋转体或与其有类似形状的四次方抛物线时，可以最大限度地减少热熔器在热熔体中流动时的阻力，在热熔钻进时易于挤压岩土体，加快成孔速度，有利于热量向土体中扩散而不是仅仅积聚在固定的几个区域，热熔区应为下小上大。当单位体积中的热功率固定时，增加热熔器的高度对钻速的影响趋于稳定，对于直径为50~60 mm热熔器的热熔区高度应在100~200 mm。在热熔器结构上应设置保径装置，保证热熔器升降通畅。热熔器的壳体应为耐高温材料，且具有良好的导热性能，能够在高温下不与熔融的热熔体产生化学反应，即高温下不易氧化。热熔器外壳材料应在不同温度值下保持绝缘性能和抗氧化性能，各部件应有相同或相近的热膨胀系数。热熔器采用电流通过具有一定电阻值的电阻产生高温作为热源，该电阻材料在空气中高温下不氧化。热熔器内正负电极在高温下应能保持其工作性能，且各部件抗热抗震性能好。热解石墨和高强石墨都可作为热熔器的发热电阻。

图2  热熔器外表面悬链线轮廓图

Fig. 2  Contour of subterrene outer surface catenary

在图1所示的热熔钻进实验台上使用挤密式热熔钻头，钻压保持5 kN不变时，改变热熔器上热功率的值，在玄武岩、凝灰岩和岩盐等致密、多孔隙的岩层中进行热熔钻进实验。

图3所示为热功率对热熔钻进速度的影响。由图3可以看出：热熔钻进速度与施加在热熔器上的热功率成正比，因为施加在热熔器上的热功率越大，则热熔钻头的温度就越高，从而对岩土体的热熔破碎效果就明显，热熔钻进速度也就越大，这一点是显而易见的，但是对于不同性质的岩土体而言其影响的程度有所不同。在本实验中，对于松散、多孔隙的凝灰岩与岩盐来说，热功率对热熔钻进速度的影响较大，而对于致密的玄武岩而言，热功率的增加对热熔钻进速度的影响较小。热功率的大小对两类不同性质岩石热熔钻进速度的影响差别较大，究其根本原因是：在凝灰岩与岩盐等松散、多孔隙岩层中进行热熔钻进时，由于施加在热熔器上的钻压的作用，使得热熔钻头是向下挤密钻进的，因此已经产生的热熔体不会集聚在孔内某处固定不动，而是能够流入到松散、多孔隙岩层的空隙中去，此时能够有效避免热熔钻头上的高温使所钻进岩层中已经热融化部分所产生的热熔体过热，需要说明的是，对于已经产生的热熔体而言，再对其继续加热的意义是不大的，只能是造成热量的白白浪费，随着热熔钻进的进行，若能够使已经产生的热熔体及时排出或远离热熔钻头作用的周遭区域(比如使已经产生的热熔体进入到松散、多孔隙岩层的空隙中)，使热熔钻头上的热能能够始终作用于未被融化的岩层上，则钻进速度自然就提高了，所以说挤压热熔体是提高热熔钻进速度的有效途径之一。实验结果表明：将土体作为热熔对象时热熔器表面的比热功率以2~3 W/cm²为宜，而将岩石作为热熔对象时，则比热功率应为40~50 W/cm²。

图3  热功率对热熔钻进速度的影响

Fig. 3  Influence of thermal power on hot melt drilling speed

使用挤密式热熔钻头，以玄武岩、凝灰岩、岩盐、散盐作为实验用地层，保持热熔器的热功率5 kW不变，改变施加在热熔器上的钻压进行热熔钻进实验，每次热熔钻进的时间是10 min。

图4所示为钻压对热熔钻进速度的影响。由图4可以看出：热熔钻进速度与钻压成正比，尤其对松散、多孔隙的凝灰岩、盐岩和散盐而言，钻压对钻进速度的影响更大些，但对于相对致密的玄武岩，钻压在0~4 kN范围内对钻速的影响较大，继续加大钻压对钻速的影响不是十分明显。资料表明：热熔钻进速度与钻压的三次开方成正比，由于热熔钻进过程中所钻成的钻孔空间大小是有限的，随着钻压的增大，热熔钻头对热熔体的挤压程度也就越强，则热熔体的厚度随之减少，但由于传热效率不变则热熔速度的提高必然使单位时间内热熔体的体积增加，其结果是更多的压力消耗在克服热熔体的水力损失上，对于一般非松散性的岩层，钻压与钻速的关系曲线变化趋缓；但对于松散、多孔隙的岩土层，钻压对钻速的影响范围更大些，实验中所采用的比钻压以0.2~1 kN/cm²为宜。

通过实验及理论分析发现：热熔器的高度越小，则热熔钻进的速度就越高，但是热熔器的高度小则热熔器内部的加热电阻元件的高度就小，产生的热功就少，有可能比热功率达不到岩土层熔化所必须的值，热熔器的高度与加热电阻元件的高度值应有一优化关系，热熔器的有效高度以180~200 mm为宜，如果加热电阻元件能够进一步改进，提高单位长度上的阻值，则这个值还可能降低。此外，随着岩土体的热导率增加，热熔钻进速度降低，原因是岩土体的热导率越强，则热能便不能积聚在热熔器周围，大量的热能会很快地传到远处，消耗在对大体积的岩土体的加热上，但是在实际中岩土体的热导率值及其变化都非常小，所以岩土体的热导率对热熔钻进速度的影响不大。

图4  钻压对热熔钻进速度的影响

Fig. 4  Influence of WOB on hot melt drilling speed

2  热熔体流动方程与遗传神经网络预测

2.1  热熔体流动方程

热熔体的流动遵循质量守恒、动量守恒和能量守恒三大定律，它们的数学描述就是热熔过程的基本方程组。热熔体流动方程的通用形式为：

    (5)

式中：ρ为热熔体的密度，与温度和压力有关；F为通用变量，它可以表示速度分量(u，v，w)、焓(h)或化学成分的浓度(c₁，c₂，c₃，…，c_n)等；Γ_F为交换系数，层流动量方程中是分子黏度，热传导方程中是热导率；S_F为产生F的源(或汇)，如动量方程中它包括压力梯度、重力及其他体积力项。

图5所示为热熔钻进及热熔体流动示意图。由图5可见：以热熔器的前端点O为原点，沿流动方向的热熔器轮廓线取作x轴，沿着热熔器表面的法线自壁面算起的距离取作y轴，以u和v表示坐标系中的x和y轴方向的速度分量。若不计重力影响，由于热熔器以等速U运动，则热熔体的运动是定常的。在单位宽度环状间隙δ上热熔体的平均流速为：

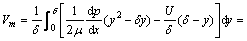
         (6)

图5  热熔钻进及热熔体流动示意图

Fig. 5  Schematic diagram of hot melt drilling and hot melt flow

由于v=0，所以热熔器与地层环状间隙中的连续性方程为：，其中Q为单位宽度的热熔体流量。

热熔器周围热熔体流动时的速度分布为：

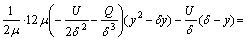
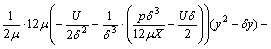
   (7)

热熔体作用在热熔器外表面上的压力为：

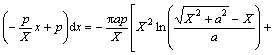
  (8)

热熔体作用在热熔器上的摩擦阻力为：

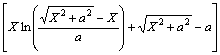    (9)

上述各热熔体流动计算方程中所采用的具体参数为：a=7.3×10^-3 m，r₀=0.025 m，H=0.075 m；U=0.000 6 m/s，γ=18 kN/m³，μ=3 550 N·s/m²，岩石密度ρ_r=2 500 kg/m³，X=a·sh(r₀/a)=0.112 m，P=γ·a·ch(r₀/a)= 279 N/m²，平均温度为1 250 ℃时的热熔体密度ρ_p=2 650 kg/m³，υ=0.002 8 m/s²，热熔体的平均厚度δ分别取1，2和3 mm，计算半径R分别取0，0.005，0.01，0.015，0.02和0.025 m。

运用上述热熔体的相关公式进行计算，得到的结果如图4 ~6所示。图7所示为热熔器表面弧长与压力的关系，图8所示为热熔器表面弧长上的热熔体对热熔器的摩擦力。

通过上述计算热熔体的相关公式及图6~8可知：在环空间隙中热熔体的流速从孔壁到热熔器表面非线性增加，在热熔器表面处的速度最大，这是由于热熔钻进时，热熔器是逐渐向下给进的，热熔钻进过程中所产生的热熔体一般来讲其黏度相对较大，当然热熔体的黏度等性质取决于具体的热熔对象的性质，热熔体的流动实际上主要是由于热熔器的向下给进对热熔体的挤压所造成的，因此热熔器的对热熔体的挤压程度对热熔体的流速影响较大，而热熔器对热熔体的挤压程度必然是距离热熔器表面越近则越强烈；由于热熔体的流动过程是蠕动，因此其流速的绝对值很小，尽管如此，但为了减少热熔钻进时热熔器运动的阻力，仍应该对热熔器的表面形状进行优化。热熔体对热熔器的压力从热熔器底部到上部也是呈一种由小到大的非线性变化规律，这是由于热熔器的表面形状采用的是悬链线形，因此所产生的环状间隙从钻孔底部至上部应呈由大到小的变化趋势，随着热熔钻进过程中热熔器的向下给进，热熔器不断挤压热熔体，则热熔体必然也会反作用于热熔器，当环状间隙越小时这种作用力也就越大；此外压力这种平滑的曲线变化，主要取决于热熔器的表面轮廓线是平滑的曲线，这对于热熔钻进时热熔器的平稳给进是非常必要的。热熔体对热熔器摩擦力的变化及产生原因同上，需要指出的是，热熔体的黏度对热熔器摩擦力的影响是相当大的。

图6  热熔体在环空间隙中的流速分布

Fig. 6  Hot melt flow rate distribution in annular gap

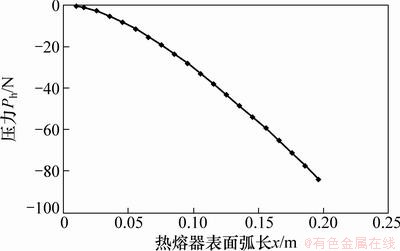
图7  热熔器表面弧长与压力的关系

Fig. 7  Relationship between surface arc length of subterrene and pressure

图8  热熔器表面弧长上的热熔体对热熔器的摩擦力

Fig. 8  Relationship between surface arc length of subterrene and friction

2.2  基于遗传神经网络的热熔体流速、热熔体对热熔器的压力及摩擦力与施加在热熔器上的热功率、钻压对热熔钻进速度影响的预测

遗传算法(genetic algorithm，GA)是一种基于自然选择与基因遗传学原理，模拟生物在自然环境下的遗传与进化过程而形成的具有自适应全局优化能力的概率搜索算法，通常用于优化神经网络的结构和学习神经网络的权值。本文将遗传算法与BP算法相融合，充分利用遗传算法的全局搜索能力和BP算法的局部搜索能力，利用遗传算法对BP神经网络进行优化。所构建的GA-BP神经网络先运用遗传算法全局搜索网络权值作为网络的初始权值，再通过神经网络训练进一步修改权值以达到精确求解的目的。GA-BP算法可分为3步：首先固定网络结构及编码生成初始种群；其次进行遗传算法进化，对个体进行选择、交叉和变异操作，并结合适应度函数求出最优个体；最后进行神经网络训练，从最优个体中提取权值和阈值作为网络初始权值和阈值，再通过网络训练更改权值直到满足系统误差要求^[7-17]。

根据参考文献[1]中论述的基于BP神经网络对热熔体在环空间隙中流速分布，热熔体对热熔器外表面压力，热熔体对热熔器摩擦力，施加在热熔器上的有效热功率及钻压在不同地层中对热熔钻进速度影响的预测，构建具有双隐含层结构的GA-BP神经网络，具体的GA-BP网络结构依据参考文献[1]中所提及的改进后具有双隐含层结构的BP网络进行设置。

将遗传算法与BP算法相融合构建了GA-BP神经网络分别对热熔体的相关数据和施加在热熔器上的有效热功率及钻压对热熔钻进速度的影响进行预测，结果表明，基于GA-BP神经网络对热熔体在环空间隙中流速的分布，热熔体作用在热熔器外表面上的压力，热熔体作用在热熔器上的摩擦力，热熔器有效热功率在不同地层中对热熔钻进速度的影响和热熔器施加不同钻压在不同地层中对热熔速度的影响的预测得到数据的均方误差比基于BP神经网络预测得到数据的均方误差分别小0.449×10^-6，0.005 6，0.001 1，0.104和0.136，且GA-BP网络比BP网络的计算时间分别短7，15， 2， 9和15 s。

图9  GA-BP算法流程图

Fig. 9  GA-BP algorithm flow chart

表1  基于BP与GA-BP神经网络的热熔体在环空间隙中流速分布的预测

Table 1  Based on BP and GA-BP neural network to predict velocity distribution of hot melt in annular clearance

表2  基于BP与GA-BP神经网络的热熔器表面弧长与热熔体对热熔器外表面压力变化的预测

Table 2  Based on BP and GA-BP neural network to predict change of arc length on subterrene surface and hot melt to outer surface of subterrene

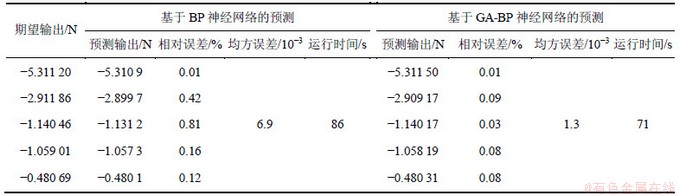
表3  基于BP与GA-BP神经网络的热熔器表面弧长与热熔体对热熔器摩擦力变化的预测

Table 3  Based on BP and GA-BP neural network to predict change of arc length on subterrene surface and friction force of hot melt on subterrene

表4  基于BP与GA-BP神经网络的热熔器有效热功率在不同地层中对热熔钻进速度影响的预测

Table 4  Based on BP and GA-BP neural network to predict impact on hot melt drilling speed of effective thermal power on subterrene

表5  基于BP与GA-BP神经网络的热熔器施加不同钻压在不同地层中对热熔钻进速度影响的预测

Table 5  Based on BP and GA-BP neural network to predict impact on hot melt drilling speed of impose different WOB on subterrene in different stratas

3  热熔钻进过程中玻璃状外壳形成研究

热熔钻进过程既有强烈的高温熔化岩土体过程，同时也伴有常规的机械挤密过程。在初始阶段是对原位岩土体的烘干、脱水(结合水的蒸发)与有机质成分燃烧等，当钻遇松散、弱胶结、多孔隙地层以及人工填土层时，不取心热熔钻具将钻孔中的岩土挤向孔壁，并在孔壁附近将其挤密，进而形成玻璃状的外壳(硬壳)，即环保型无套管孔壁。

孔壁周围形成硬壳厚度为：

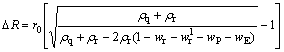 (10)

式中：r₀为钻孔最大半径，m；ρ_q为石英密度，2 650 kg/m³；ρ_r为原位(天然)岩土体的密度，1 800 kg/m³；w_r为原位岩土重力水含水率，0.15 kg/kg；w¹_r为原位岩土结合水含水率，0.05 kg/kg；w_P为原位岩土中有机质和其他可燃成分质量分数，0.03 kg/kg；w_E为在相应高温下原位岩土挥发成分质量分数，0.02 kg/kg，由式(10)可以看出：孔壁周围形成的硬壳厚度与钻孔的最大半径成正比，这完全相当于一个物理过程，即热力作用弱化、松动了一部分岩土体，另一部分岩土体被迫挤向孔壁，还有一部分岩土体形成硬壳。一般情况下采用的热功率和钻压正比于钻孔直径的平方。当采用直径为50，76，93及120 mm的热熔器进行热熔钻进实验时，通过计算，其孔壁周围所形成的硬壳厚度ΔR依次为14.9，22.6，27.7及35.7 mm，这与实测结果是基本相符的。

通常来说，热力作用岩石不同温度下的稳定性可分为3类，即小于1 000 ℃时的低温区、处于1 000~1 500 ℃时的中等温度区以及大于1 500 ℃时的高温区，这一点同样适用于热熔钻进过程。热熔钻进过程中，伴随着温度场的变化，需要考虑岩土体的2个变化过程，既有渐进过程，也有衰退过程。渐进过程指高温度和高钻压，衰退过程温度和钻压变化正好相反。岩土体在热力作用下状态变化形成光晕的过程明显伴随着温度渐进和衰退，而在实际热熔钻进中最终岩土体变化的产物积聚在孔壁周围，也是由这2个过程形成第1阶段的热熔器的平移与紧随其后的第2阶段的冷却结晶成型。渐进和衰退的温度场变化参数确定了热熔器的工作温度、钻压及其移动速度。矿物质将进一步随着温度场的提高而形成，不同温度形成的物质也将不同。分析热熔钻进过程中孔壁周围玻璃状外壳(硬壳)的形成机制时，必须要考虑钻孔周围岩土体状态的变化情况，确定不均质硬壳中的物质成分及其结构特点，应将中等温度区岩土体的变化情况作为研究的重点，对整个热熔钻进过程中岩土体变化规律的研究可以借鉴制造陶瓷或耐火材料的工艺原理，同时还可以借鉴矿物学或岩石学的已有成果，使热熔钻进工艺日臻完善。

4  结论

(1) 横截面为圆形，纵向截面为悬链线旋转体或与其有类似形状的四次方抛物线是热熔器设计中较为优良的结构形式，给出了有关热熔器结构方面计算的一系列经验公式；探讨了制作热熔器时所采用的壳体与电阻材料及其所应具备的性能。使用挤密式热熔钻头进行的热熔钻进实验表明，热熔钻进速度与施加在热熔器上的热功率及钻压均成正比，且这种影响规律在松散、多孔隙地层中表现的更为明显。实际热熔钻进时，热熔器的有效高度以180~200 mm为宜，此外岩土体的热导率对热熔钻进速度的影响不大。

(2) 建立了热熔器周围环空中的热熔体流动时的速度分布，热熔体作用在热熔器外表面上的压力，热熔体作用在热熔器上的摩擦力的数学模型，结合实验过程中的具体条件计算得出了上述热熔体相关问题数学模型的解析解，并绘制出了相应的关系曲线图，揭示了有关热熔体在环空中流动时的速度分布、热熔体对热熔器的压力及热熔体对热熔器的摩擦力的规律，并分析了产生这些现象的原因。事实表明，运用所构建的数学模型计算得到的有关热熔体一系列相应参数值的变化规律与实际情况是一致的，说明所建立的数学模型是可靠的。通过对热熔体的相关数据和施加在热熔器上的有效热功率及钻压对热熔钻进速度影响的实验数据运用神经网络模型进行预测，其预测精度在研究所能接受的范围之内，表明将该方法用于热熔钻的研究是可行的。对比分析基于GA-BP神经网络与基于BP神经网络的预测结果可以发现，基于GA-BP神经网络所得结果的预测精度比基于BP神经网络的高，且GA-BP神经网络的运行计算时间短。

(3) 对热熔钻进过程中玻璃状外壳(硬壳)的形成进行了探讨，并给出了孔壁周围形成硬壳厚度的经验公式，结合实验过程中具体的相关参数，采用该公式计算得到的硬壳厚度与实测结果基本一致，说明该经验公式是可靠的。此外，对于热熔钻进过程中孔壁周围玻璃状外壳(硬壳)的形成，应着重研究中等温度区岩土体的变化情况。

参考文献：

[1] 温继伟, 陈晨. 神经网络及数值模拟技术在热熔钻中的应用[J]. 金属矿山, 2012(5): 21-26.

WEN Jiwei, CHEN Chen. Application of neural network and numerical simulation technology in hot melt drilling[J]. Metal Mine, 2012(5): 21-26.

[2] 陈晨, 张祖培, 刘宝林, 等. 热熔钻进过程中温度在土体中传递规律的研究[J]. 探矿工程: 岩土钻掘工程, 2001(增刊): 172-174.

CHEN Chen, ZHANG Zupei, LIU Baolin, et al. Study of the temperature transfer law in the soil of the hot melt drilling[J]. Exploration Engineering, 2001(Suppl): 172-174.

[3] 陈晨, 张祖培, 卢文阁, 等. 工程陶瓷及特种石墨在热熔器结构设计中的应用[J]. 吉林大学学报: 地球科学版, 2004, 34(4): 643-647.

CHEN Chen, ZHANG Zupei, LU Wenge, et al. The application of engineering ceramics and special graphite in construction design of sub terrene drills[J]. Journal of Jilin University: Earth Science Edition, 2004, 34(4): 643-647.

[4] 汪晓锋, 张祖培, 陈晨. 热熔钻进新技术[J]. 岩土工程技术, 2002, 2: 123-125.

WANG Xiaofeng, ZHANG Zupei, CHEN Chen. New technology of hot melt drilling[J]. Geotechnical Engineering Technique, 2002, 2: 123-125.

[5] 张祖培, 殷琨, 蒋荣庆, 等. 岩土钻掘工程新技术[M]. 北京: 地质出版社, 2003: 9-15.

ZHANG Zhupei, YIN Kun, JIANG Rongqing, et al. The technology of drilling & tunneling[M]. Beijing: Geological Publishing House, 2003: 9-15.

[6] 汤凤林, Kudriashov B B. 热熔钻进方法及其在工程施工中的应用[J]. 地质科技情报, 2000, 19(2): 64-66.

TANG Fenglin, Kudriashov B B. Hot melt drilling method and its application in engineering installation[J]. Geological Science and Technology Information, 2000, 19(2): 64-66.

[7] 刘立鹏, 王伟, 董培欣, 等. 基于遗传神经网络的焊接接头力学性能预测系统[J]. 焊接学报, 2011, 32(7): 105-108.

LIU Lipeng, WANG Wei, DONG Peixin, et al. Mechanical properties predication system for welded joints based on neural network optimized by genetic algorithm[J]. Transactions of the China Welding Institution, 2011, 32(7): 105-108.

[8] 单永志, 尹健, 许河川, 等. 基于遗传神经网络的反跑道子弹药落点散布研究[J]. 弹道学报, 2012, 24(2): 56-57.

SHAN Yongzhi, YIN Jian, XU Hechuan, et al. Study on distribution of anti-runway submunition based on artificial neural network[J]. Journal of Ballistics, 2012, 24(2): 56-57.

[9] 李满峰, 李素萍, 范波. 基于遗传神经网络的太阳能集热器仿真研究[J]. 中国电机工程学报, 2012, 32(5): 126-130.

LI Manfeng, LI Suping, FAN Bo. Research on solar collector simulation based on Genetic-BP algorithm[J]. Proceedings of the CSEE, 2012, 32(5): 126-130.

[10] 陈海燕, 蔡嗣经, 郑明贵. 中国能源可持续发展的遗传神经网络评价[J]. 太阳能学报, 2010, 31(9): 1220-1224.

CHEN Haiyan, CAI Sijing, ZHENG Minggui. Evaluation of China’s sustainable development of energy based on GA-BP model[J]. ACTA Energiae Solaris Sinica, 2010, 31(9): 1220-1224.

[11] 吴令, 姜周华, 龚伟, 等. 基于遗传神经网络的多元渣系活度预测模型[J]. 东北大学学报: 自然科学版, 2008, 29(12): 1725-1728.

WU Ling, JIANG Zhouhua, GONG Wei, et al. GA-NN-Based predicting model of activity of multiple slag system[J]. Journal of Northeastern University: Natural Science, 2008, 29(12): 1725-1728.

[12] 付天亮, 王昭东, 王国栋, 等. 修正遗传神经网络预测中厚板轧机轧制力[J]. 东北大学学报: 自然科学版, 2008, 29(10): 1438-1442.

FU Tianliang, WANG Zhaodong, WANG Guodong, et al. Application of modified GA-ANN network to rolling force prediction[J]. Journal of Northeastern University: Natural Science, 2008, 29(10): 1438-1442.

[13] 韩飞, 莫健华, 龚攀. 基于遗传神经网络的数字化渐进成形回弹预测[J]. 华中科技大学学报: 自然科学版, 2008, 36(1): 121-124.

HAN Fei, MO Jianhua, GONG Pan. Incremental sheet NC forming springback prediction using genetic neural network[J]. J Huazhong Univ of Sci & Tech: Natural Science Edition, 2008, 36(1): 121-124.

[14] 朱凯, 王正林. 精通MATLAB神经网络[M]. 北京: 电子工业出版社, 2010: 193-199.

ZHU Kai, WANG Zhenglin. Proficient in MATLAB neural network[M]. Beijing: Electronic Industry Press, 2010: 193-199.

[15] 傅荟璇, 赵红. MATLAB神经网络应用设计[M]. 北京: 机械工业出版社, 2010: 83-92.

FU Huixuan, ZHAO Hong. MATLAB neural network application design[M]. Beijing: China Machine Press, 2010: 83-92.

[16] 史峰, 王小川, 郁磊, 等. MATLAB神经网络30个案例分析[M]. 北京: 北京航空航天大学出版社, 2010: 1-18.

SHI Feng, WANG Xiaochuan, YU Lei, et al. MATLAB neural network analysis of 30 cases[M]. Beijing: Beijing Aeronautics and Astronautics Press, 2010: 1-18.

[17] 施彦, 韩力群, 廉小亲. 神经网络设计方法与实例分析[M]. 北京: 北京邮电大学出版社, 2009: 23-36.

SHI Yan, HAN Liqun, LIAN Xiaoqin. Neural network design and case analysis[M]. Beijing: Beijing University of Posts and Telecommunications Press, 2009: 23-36.

(编辑  陈爱华)

收稿日期：2013-03-15；修回日期：2013-05-25

基金项目：科技部中俄科技合作专项(3G0085364424)

通信作者：陈晨(1965-)，男，四川资中人，教授，博士生导师，从事岩土工程钻凿技术与计算机模拟，基础工程设计、施工与数值模拟研究；电话：0431-88502337；E-mail：chenchen@jlu.edu.cn