钛合金中α片层球化分数敏感性分析
来源期刊:中国有色金属学报(英文版)2019年第2期
论文作者:罗皎 王博哲 王林风 李莲 李淼泉
文章页码:305 - 312
关键词:钛合金;敏感性分析;球化分数;遗传算法
Key words:titanium alloys; sensitivity analysis; globularized fraction; genetic algorithm
摘 要:基于机理型微观组织模型与梯度算法建立钛合金中α片层球化分数敏感性分析函数,将该函数应用于TC17合金中片层组织球化分数的敏感性分析。基于扫描电镜观测结果定量分析TC17合金等温压缩过程中工艺参数对球化分数的影响规律,并采用遗传算法优化其敏感性分析函数的材料参数。结果表明:当变形温度为1083 K、应变速率为0.01 s-1、应变为1.2时,TC17合金片层α组织几乎完全转变为等轴α晶粒;随着应变速率的增加,片层α球化分数减少,这主要因为较低的应变速率为动态球化提供了足够的时间;而变形温度对片层α球化分数的影响受应变速率控制。此外,TC17合金片层α球化分数关于应变、变形温度和对数应变速率微分的预测结果与试验结果相吻合。
Abstract: The sensitivity analysis functions on globularized fraction of α lamellae were established using a physically-based microstructure model and gradient method. These functions were applied to the sensitivity analysis on globularized fraction of α lamellae in TC17 alloy. The material constants in these functions are determined using the genetic algorithm-based objective optimization technique. The globularized fraction of α lamellae during isothermal compression of TC17 alloy was quantitatively analyzed based on scanning electron microscopy (SEM) observation. The results show that α lamellae mostly change to equiaxed α grains at a deformation temperature of 1083 K, a strain rate of 0.01 s-1 and a strain of 1.2. The globularized fraction decreases with increasing strain rate because lower strain rate provides enough time for the spheroidization. The effect of deformation temperature on the globularized fraction is controlled by the strain rate. And, the predicted derivations of globularized fraction with respect to processing parameters show good agreement with the experimental values.
Trans. Nonferrous Met. Soc. China 29(2019) 305-312
Jiao LUO, Bo-zhe WANG, Lin-feng WANG, Lian LI, Miao-quan LI
School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China
Received 20 November 2017; accepted 11 April 2018
Abstract: The sensitivity analysis functions on globularized fraction of α lamellae were established using a physically-based microstructure model and gradient method. These functions were applied to the sensitivity analysis on globularized fraction of α lamellae in TC17 alloy. The material constants in these functions are determined using the genetic algorithm-based objective optimization technique. The globularized fraction of α lamellae during isothermal compression of TC17 alloy was quantitatively analyzed based on scanning electron microscopy (SEM) observation. The results show that α lamellae mostly change to equiaxed α grains at a deformation temperature of 1083 K, a strain rate of 0.01 s-1 and a strain of 1.2. The globularized fraction decreases with increasing strain rate because lower strain rate provides enough time for the spheroidization. The effect of deformation temperature on the globularized fraction is controlled by the strain rate. And, the predicted derivations of globularized fraction with respect to processing parameters show good agreement with the experimental values.
Key words: titanium alloys; sensitivity analysis; globularized fraction; genetic algorithm
1 Introduction
It is well known that the mechanical properties of titanium alloys are strongly affected by the microstructural characteristics (e.g., the volume fraction of various phases, grain size, and grain misorientation). During high temperature deformation, the alloys undergo significant microstructural changes including dynamic recrystallization or recovery and grain growth. The microstructural evolution is very sensitive to the processing parameters, and strongly affects the mechanical properties [1-4]. Therefore, it is very important to obtain the law of the microstructural evolution, and make the sensitivity analysis of microstructure with respect to processing parameters so as to control the microstructure.
In recent years, extensive efforts were paid to simulating the microstructural evolution and making the sensitivity analysis of microstructure for a wide range of metals and alloys [5]. KOHAR et al [6] established a new multi-scale framework which incorporated the microstructural evolution, and stimulated texture evolution in single crystal and polycrystal FCC material. FULLWOOD et al [7] got the microstructure-property relations in Fourier form, leading to an efficient spectral framework of sensitive analysis and designing for microstructure. McDOWELL and DUNNE [8] developed the microstructure-sensitive model and facilitated parametric design exploration in searching for morphologies and/or compositions that modified fatigue resistance. Much prior work showed that the sensitivity analysis of microstructure was made based on the empirical microstructure model and finite element simulation. Although these sensitivity analyses could provide a optimization scheme to control the microstructure and design the processing parameters during deformation, the empirical microstructure model cannot reveal the plastic deformation mechanisms of metals and alloys. It is well known that the physically-based microstructure model is not only highly reliable in predicting microstructure, but it can also reveal the plastic deformation mechanisms.
Therefore, the object of the present work is to make the sensitivity analysis of microstructure with respect to processing parameters with the aid of physically-based microstructure model of titanium alloys. For this purpose, the gradient functions are expressed as the sensitivities of strain, deformation temperature and strain rate with respect to globularized fraction of α lamellae. Applying the sensitivity analysis to high temperature deformation process of TC17 alloy, the sensitivity domains of the globularized fraction are confirmed to control the microstructure in the present work.
2 Experimental
The 50 mm-in-diameter billets of TC17 alloy had chemical composition (wt.%) of 5.12 Al, 2.03 Sn, 2.10 Zr, 4.04 Mo, 3.94 Cr, 0.10 Fe, 0.12 C, 0.007 N, 0.007 H, 0.12 O, and balanced Ti. TC17 alloy containing lamellar α microstructure was compressed at the deformation temperatures of 1043, 1063, 1083, 1103 and 1123 K, the strain rates of 0.01, 0.1, 1.0 and 5.0 s-1, and the strains of 0.2, 0.5, 0.7, 0.9 and 1.2. A thermocouple was welded on the surface of the specimens to measure the temperature during deformation, and graphite powder was put between the specimens and the anvils to reduce die friction. After isothermal compression, the specimens were water-quenched to room temperature. To observe deformed microstructure, the specimens were mechanically polished and chemically etched in a solution of 10 mL HF, 15 mL HNO3 and 75 mL H2O. A Zeiss SUPRA 55 SEM operating at 20 kV was used to examine the microstructural evolution of lamellar α microstructure in TC17 alloy. The SEM micrographs were taken along the direction perpendicular to the compression axis. The globularized fraction of lamellar α microstructure in TC17 alloy was measured using quantitative metallography image analysis software (Image-Pro Plus 6.0), and it was calculated by the average value of twenty visual fields.
3 Sensitivity analysis of globularized fraction
In the present work, it is assumed that the globularized fraction follows an Avrami type equation [9,10]:
 (1)
(1)
where X(t) is the globularized fraction at time t; G is the growth rate of globular grain (m/s); NV is the number of globular grain per unit volume, and it is given by [10,11]
 (2)
(2)
where S0 is the initial surface area per unit volume (μm-1), t is the time (s), 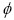 is the material constant (s-1), and d is the size of globular grain (μm).
is the material constant (s-1), and d is the size of globular grain (μm).
G is expressed as [12,13]
 (3)
(3)
where Mgb is the grain boundary mobility (m4·J-1·s-1), σsurf is the grain boundary energy per unit area (J/m2), b is the magnitude of Burgers vector (2.86×10-10 m), δ is the characteristic grain boundary thickness (m), D0 is the self-diffusion constant, k is Boltzmann’s constant (1.381×10-23 J/K), and Qpd is the boundary diffusion activation energy (kJ/mol).
If the deformation is performed at a constant strain rate, there is
 (4)
(4)
where ε is the strain, and  is the strain rate (s-1).
is the strain rate (s-1).
By substituting Eqs. (2)-(4) into Eq. (1), the globularized fraction X is written as
 (5)
(5)


According to the transformation kinetics law, the globularized fraction X is modified by
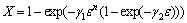 (6)
(6)
where n is the kinetics exponent; γ1 and γ2 are the material constants.
In addition, the Zener-Hollomon parameter is introduced into Eq. (6) to describe the effect of deformation temperature and strain rate on the globularized fraction X. Finally, the globularized fraction X is written in the following form:
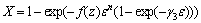 (7)
(7)
where f(z)=pZm;  ; p, m and γ3 are the material constants; Q is the apparent activation energy for deformation (kJ/mol), R is the gas constant (8.3145 J·mol-1·K-1); T is the absolute deformation temperature (K).
; p, m and γ3 are the material constants; Q is the apparent activation energy for deformation (kJ/mol), R is the gas constant (8.3145 J·mol-1·K-1); T is the absolute deformation temperature (K).
By differentiating Eq. (7), the gradients of the globularized fraction X with respect to the strain, the deformation temperature and the lg(strain rate) are calculated as

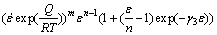 (8)
(8)

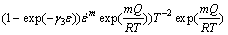 (9)
(9)
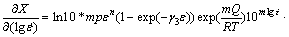
 (10)
(10)
From Eqs. (8)-(10), it is seen that these gradient functions can be used for the sensitivity analysis of globularized fraction during high temperature deformation of titanium alloys.
4 Applying functions of sensitivity analysis to lamellar α microstructure in TC17 alloy
4.1 Effect of processing parameters on globularized fraction

Fig. 1 Effect of processing parameters on globularized fraction of lamellar α microstructure in TC17 alloy (a, b) and SEM micrographs with different processing parameters (c-h)
The globularization behavior of lamellar α microstructure in TC17 alloy is quantified with the aid of SEM observations and quantitative metallography image analysis software. Figure 1 shows the globularized fraction as a function of strain, deformation temperature and strain rate. At a deformation temperature of 1083 K and a strain rate of 0.01 s-1, the globularized fraction significantly increases from 0.07 to 0.68 when the strain increases from 0.2 to 1.2. The SEM micrographs at the strains of 0.2 and 1.2 are shown in Fig. 1(c) and Fig. 1(d), respectively. In Fig. 1(c), the parallel α lamellae are present in this alloy, without the formation of significant equiaxed α grains. At a strain of 1.2, almost fully equiaxed microstructure that contains only a small amount of unglobularized α lamellae is provided in Fig. 1(d), suggesting the fragmentation and globula- rization of α lamellae via groove/boundary splitting under this condition [14-16]. At the strain rates of 1.0 and 5.0 s-1, the globularized fraction of TC17 alloy also shows a similar increase with increasing strain, but the increasing extent at the strain rates of 1.0 and 5.0 s-1 decreases, as illustrated in Fig. 1(a).
Figure 1(b) shows the effect of deformation temperature on the globularized fraction of lamellar α microstructure in TC17 alloy. At a strain rate of 0.01 s-1 and a strain of 0.9, the globularized fraction significantly increases from 0.12 to 0.62 when the deformation temperature increases from 1043 to 1103 K. Figures 1(e) and (f) show the SEM micrographs at the deformation temperatures of 1043 and 1103 K, respectively. At 1043 K (Fig. 1(e)), the microstructure is comprised of the parallel α lamellae and β phase. When the deformation temperature is up to 1103 K (Fig. 1(f)), the microstructure is comprised of equiaxed α grains, a small amount of unglobularized α lamellae and β phase, consistent with the quantitative results above. This phenomenon demonstrates that the deformation temperature has a significant effect on the globularized fraction of TC17 alloy at a strain rate of 0.01 s-1 and a strain of 0.9. However, the quantitative results of the globularized fraction reveal a weak dependence on the deformation temperature at the strain rate of 1.0 and 5.0 s-1. Main reason is that lower strain rate provides enough time for the spheroidization of lamellar α microstructure in TC17 alloy, and higher deformation temperature is beneficial for the diffusion of solutes. So, enough time and high solute diffusion promote a significant increase in globularized fraction of lamellar α microstructure in TC17 alloy.
In addition, it is seen that the globularized fraction of lamellar α microstructure in TC17 alloy decreases with increasing strain rate, as illustrated in Figs. 1(a) and (b). This phenomenon can also be confirmed by the SEM micrographs in Figs. 1(f)-(h). It is seen in Figs. 1(f)-(h) that equiaxed α grains decrease with increasing strain rate. Figure 1(h) shows that a few bent and kinked α lamellae are present under this condition, and α lamellae are parallel along the direction perpendicular to the compression axis. At a strain rate of 5.0 s-1 (Fig. 1(h)), only parallel α lamellae are observed. This is possibly due to lower strain rate providing enough time for the spheroidization. The above results and analyses indicate that the globularization behavior of lamellar α microstructure in TC17 alloy is highly dependent on the strain and strain rate during deformation. However, the effect of deformation temperature on the globularization behavior of lamellar α microstructure in TC17 alloy is controlled by the strain rate.
4.2 Identification of material constants in gradient functions
The measurements of the globularized fraction as a function of strain, deformation temperature and strain rate of lamellar α microstructure in TC17 alloy are shown in Fig. 1. Based on these measured values, the derivatives of the fraction globularized with respect to processing parameters (strain, deformation temperature, lg(strain rate)) can be obtained as the experimental data. Using conventional optimization method, it is difficult to determine the material constants in the gradient functions (Eqs. (8)-(10)). The material constants in these gradient functions are determined using the GA-based objective optimization technique [17,18]. The objective functions are expressed as
 (11)
(11)
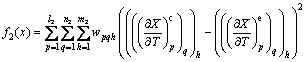 (12)
(12)

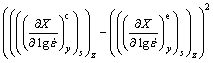 (13)
(13)
where ε is the strain; T is the deformation temperature (K);  is the strain rate (s-1); f1(x), f2(x) and f3(x) are the residuals for the derivatives of the globularized fraction with respect to strain, deformation temperature and lg(strain rate), respectively; X is the globularized fraction;
is the strain rate (s-1); f1(x), f2(x) and f3(x) are the residuals for the derivatives of the globularized fraction with respect to strain, deformation temperature and lg(strain rate), respectively; X is the globularized fraction; 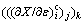 and
and  are the predicted and experimental derivatives of the globularized fraction with respect to strain at strain i, strain rate j and deformation temperature k; m1 is the number of strain; n1 is the number of strain rate; l1 is the number of deformation temperature; wijk is the weight coefficient. Similarly,
are the predicted and experimental derivatives of the globularized fraction with respect to strain at strain i, strain rate j and deformation temperature k; m1 is the number of strain; n1 is the number of strain rate; l1 is the number of deformation temperature; wijk is the weight coefficient. Similarly,  and
and 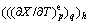 are the predicted and experimental derivatives of the globularized fraction with respect to deformation temperature at time p, strain rate q and deformation temperature h; m2 is the number of strain; n2 is the number of strain rate; l2 is the number of deformation temperature; wpqh is the weight coefficient.
are the predicted and experimental derivatives of the globularized fraction with respect to deformation temperature at time p, strain rate q and deformation temperature h; m2 is the number of strain; n2 is the number of strain rate; l2 is the number of deformation temperature; wpqh is the weight coefficient. 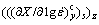 and
and  are the predicted and experimental derivatives of the globularized fraction with respect to lg(strain rate) at time y, strain rate s and deformation temperature z; m3 is the number of strain; n3 is the number of strain rate; l3 is the number of deformation temperature; wysz is the weight coefficient. Finally, the material constants in Eqs. (8)-(10) are listed in Table 1.
are the predicted and experimental derivatives of the globularized fraction with respect to lg(strain rate) at time y, strain rate s and deformation temperature z; m3 is the number of strain; n3 is the number of strain rate; l3 is the number of deformation temperature; wysz is the weight coefficient. Finally, the material constants in Eqs. (8)-(10) are listed in Table 1.
Table 1 Material constants in gradient functions of lamellar α microstructure in TC17 alloy

4.3 Comparison of predicted data with experimental data
Using the material constants in Table 1, the derivatives of the globularized fraction with respect to processing parameters (strain, deformation temperature, and lg(strain rate)) are predicted. Figure 2 shows the comparison of the predicted with the experimental  X/
X/ ε. It is seen that the average relative differences for the sample data and the non-sample data are 8.8% and 11.8%, respectively. Figure 3 shows the comparison of the predicted with the experimental
ε. It is seen that the average relative differences for the sample data and the non-sample data are 8.8% and 11.8%, respectively. Figure 3 shows the comparison of the predicted with the experimental  X/
X/ T. It is seen that the average relative differences for the sample data and the non-sample data are 9.2% and 10.4%, respectively. Figure 4 shows the comparison of the predicted with the experimental
T. It is seen that the average relative differences for the sample data and the non-sample data are 9.2% and 10.4%, respectively. Figure 4 shows the comparison of the predicted with the experimental  . It is seen that the average relative differences for sample data and non-sample data are 8.1% and 11.3%, respectively. The above results indicate that these gradient functions with a high prediction precision can be used to predict the derivatives of the globularized fraction with respect to processing parameters in TC17 alloy containing lamellar α microstructure.
. It is seen that the average relative differences for sample data and non-sample data are 8.1% and 11.3%, respectively. The above results indicate that these gradient functions with a high prediction precision can be used to predict the derivatives of the globularized fraction with respect to processing parameters in TC17 alloy containing lamellar α microstructure.
4.4 Sensitivity domains of globularized fraction in TC17 alloy
Based on the predicted derivatives of the globularized fraction with respect to processing parameters, the sensitivity domains of lamellar α microstructure in TC17 alloy are confirmed. Figure 5 shows the predicted curves for the derivatives of globularized fraction with respect to processing parameters, implying that the predicted values show good agreement with the experimental results. In Fig. 5(a), it is seen that the derivative of globularized fraction with respect to strain decreases with increasing strain after a peak value. The possible reason is that large strain produces very high dislocation accumulation and local dislocation tangles in early stage of deformation, which promotes the formation of low-angle boundaries (LABs) in α lamella interiors and finally results in the occurrence of the fragmentation and globularization of α lamellae via groove/boundary splitting. Thus, the derivative of globularized fraction with respect to strain firstly increases with increasing strain. However, continuous fragmentation and globularization of α lamellae become more difficult after a certain globularized degree due to the fact that most plastic deformation energy is used for the grain boundary sliding of equiaxed α grains in the late stage of deformation [19]. So, the derivative of globularized fraction with respect to strain decreases with increasing strain after a peak value. In addition, it is seen that the derivative value of globularized fraction with respect to strain at a deformation temperature of 1083 K and a strain rate of 0.01 s-1 is the largest when the strain is in the range of 0.7-1.2, implying that the globularized fraction of lamellar α microstructure in TC17 alloy is the most sensitive to the strain at this deformation temperature and strain rate. The above analysis indicates that the globularization behavior of lamellar α microstructure in TC17 alloy is very noticeable if the deformation is performed in these sensitivity domains.

Fig. 2 Comparison of predicted with experimental  X/
X/ ε
ε

Fig. 3 Comparison of predicted with experimental  X/
X/ T
T

Fig. 4 Comparison of predicted with experimental 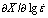
In Fig. 5(b), it is seen that the derivative of globularized fraction with respect to deformation temperature has a general increasing tendency. This is possibly attributed to the fact that the globularization process is greatly affected by the diffusion-controlled interface migration. The interface migration that is a thermally-activated process is influenced by the deformation temperature. Thus, the derivative of globularized fraction with respect to deformation temperature has a general increasing tendency with increasing deformation temperature. In addition, the derivative value of globularized fraction with respect to deformation temperature at a strain of 0.9 and a strain rate of 0.1 s-1 is the largest when the deformation temperature is in the range of 1063-1103 K, implying that the globularized fraction of lamellar α microstructure in TC17 alloy is the most sensitive to the deformation temperature at this strain and strain rate. The above analysis indicates that the globularization behavior of lamellar α microstructure in TC17 alloy is very noticeable if the deformation is performed in these sensitivity domains.
In Fig. 5(c), it is seen that the absolute derivative of globularized fraction with respect to lg(strain rate) decreases with increasing strain rate. Main reason is that lower strain rate provides enough time for the spheroidization of lamellar α microstructure in TC17 alloy. In addition, the absolute derivative value of globularized fraction with respect to lg(strain rate) at a strain of 0.9 and a deformation temperature of 1083-1103 K is the largest when the strain rate is in the range of 0.01-0.1 s-1, implying that the globularized fraction of lamellar α microstructure in TC17 alloy is the most sensitive to the strain rate at this strain and in this deformation temperature range. The above analysis indicates that the globularization behavior of TC17 alloy containing lamellar α microstructure is very noticeable if the deformation is performed in these sensitivity domains.
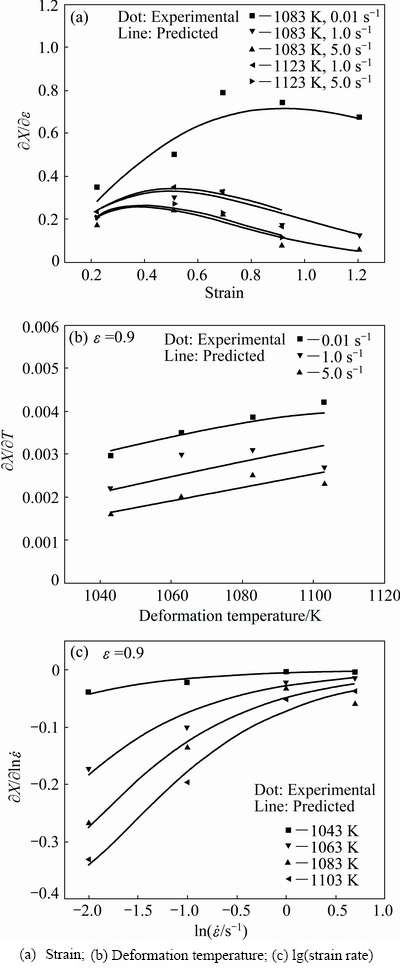
Fig. 5 Predicted curves for derivatives of globularized fraction with respect to processing parameters
5 Conclusions
(1) When the strain increases to 1.2, the α lamellae mostly change to equiaxed α grains at 1083 K and 0.01 s-1, suggesting the fragmentation and globulari- zation of α lamellae via groove/boundary splitting.
(2) The globularized fraction decreases with increasing strain rate because lower strain rate provides enough time for the spheroidization. The effect of deformation temperature on the fraction globularized is controlled by strain rate.
(3) The gradient functions of the globularized fraction with respect to the strain, the deformation temperature and the lg(strain rate) are obtained. The results indicate that these gradient functions with a high prediction precision can be used to predict the derivatives of the globularized fraction with respect to processing parameters in TC17 alloy containing lamellar α microstructure.
References
[1] GAO Peng-fei, YANG He, FAN Xiao-guang, LEI Zhen-ni, CAI Yang. Prediction of tri-modal microstructure under complex thermomechanical processing history in isothermal local loading forming of titanium alloy [J]. Transactions of Nonferrous Metals Society of China, 2017, 27: 2423-2433.
[2] LAN Chun-bo, LI Guo, WU Yu, GUO Li-li, CHEN Feng. Effects of cold deformation on microstructure and mechanical properties of Ti-35Nb-2Zr-0.3O alloy for biomedical applications [J]. Transactions of Nonferrous Metals Society of China, 2017, 27: 1537-1542.
[3] TARZIMOGHADAM Z, SANDLOBES S, PRADEEP K G, RAABE D. Microstructure design and mechanical properties in a near-α Ti-4Mo alloy [J]. Acta Materialia, 2015, 97: 291-304.
[4] LI Hui-min, LI Miao-quan, LUO Jiao, WANG Ke. Microstructure and mechanical properties of heat-treated Ti-5Al-2Sn-2Zr-4Mo- 4Cr [J]. Transactions of Nonferrous Metals Society of China, 2015, 25: 2893-2900.
[5] GUAN Jing, WANG Guang-chun, ZHAO Guo-qun. The microstructure optimal design using sensitivity analysis methods in forging process [J]. Journal of Plasticity Engineering, 2007, 14: 6-10.
[6] KOHAR C P, BASSANI J L, BRAHME A, MUHAMMAD W, MISHRA R K, INAL K. A new multi-scale framework to incorporate microstructure evolution in phenomenological plasticity: Theory, explicit finite element formulation, implementation and validation [J]. International Journal of Plasticity, Available Online, DOI: http://doi.org/10.1016/j.ijplas.2017.08.006.
[7] FULLWOOD D T, NIEZGODA S R, ADAMS B L, KALIDINDI S R. Microstructure sensitive design for performance optimization [J]. Progress in Materials Science, 2010, 55: 477-562.
[8] McDOWELL D L, DUNNE F P E. Microstructure-sensitive computational modeling of fatigue crack formation [J]. International Journal of Fatigue, 2010, 32: 1521-1542.
[9] SONG Hong-wu, ZHANG Shi-hong, CHENG Ming. Dynamic globularization kinetics during hot working of a two phase titanium alloy with a colony alpha microstructure [J]. Journal of Alloys and Compounds, 2009, 480: 922-927.
[10] SELLARS C M, ZHU Q. Microstructural modelling of aluminium alloys during thermomechanical processing [J]. Materials Science and Engineering A, 2000, 280: 1-7.
[11] ROBERTS W, BODEN H, AHLBLOM B. Dynamic recrystallization kinetics [J]. Metal Science Journal, 2013, 13: 195-205.
[12] SHEWMON P G. Transformation in metals [M]. New York: McGraw-Hill, 1969.
[13] DING R, GUO Z X. Microstructural modelling of dynamic recrystallisation using an extended cellular automaton approach [J]. Computational Materials Science, 2002, 23: 209-218.
[14] FAN Xiao-guang, YANG He, GAO Peng-fei, ZUO Rui, LEI Peng-hui, JI Zhe. Morphology transformation of primary strip α phase in hot working of two-phase titanium alloy [J]. Transactions of Nonferrous Metals Society of China, 2017, 27: 1294-1305.
[15] MIRONOV S, MURZINOVA M, ZHEREBTSOV S, SALISHCHEV G A, SEMIATIN S L. Microstructure evolution during warm working of Ti-6Al-4V with a colony-α microstructure [J]. Acta Materialia, 2009, 57: 2470-2481.
[16] WEISS I, FROES F H, EYLON D, WELSCH G E. Modification of alpha morphology in Ti-6Al-4V by thermomechanical processing [J]. Metallurgical Transactions A, 1986, 17: 1935-1947.
[17] LUO Jiao, LI Miao-quan, LI Xiao-li, SHI Yan-pei. Constitutive model for high temperature deformation of titanium alloys using internal state variables [J]. Mechanics of Materials, 2010, 42: 157-165.
[18] LIN J, YANG J B. GA-based multiple objective optimisation for determining viscoplastic constitutive equations for superplastic alloys [J]. International Journal of Plasticity, 1999, 15: 1181-1196.
[19] KIM J H, SEMIATIN S L, LEE C S. Constitutive analysis of the high-temperature deformation of Ti-6Al-4V with a transformed microstructure [J]. Acta Materialia, 2003, 51: 5613-5626.
罗 皎,王博哲,王林风,李 莲,李淼泉
西北工业大学 材料学院,西安 710072
摘 要:基于机理型微观组织模型与梯度算法建立钛合金中α片层球化分数敏感性分析函数,将该函数应用于TC17合金中片层组织球化分数的敏感性分析。基于扫描电镜观测结果定量分析TC17合金等温压缩过程中工艺参数对球化分数的影响规律,并采用遗传算法优化其敏感性分析函数的材料参数。结果表明:当变形温度为1083 K、应变速率为0.01 s-1、应变为1.2时,TC17合金片层α组织几乎完全转变为等轴α晶粒;随着应变速率的增加,片层α球化分数减少,这主要因为较低的应变速率为动态球化提供了足够的时间;而变形温度对片层α球化分数的影响受应变速率控制。此外,TC17合金片层α球化分数关于应变、变形温度和对数应变速率微分的预测结果与试验结果相吻合。
关键词:钛合金;敏感性分析;球化分数;遗传算法
(Edited by Bing YANG)
Foundation item: Project (51575446) supported by the National Natural Science Foundation of China; Project (2016JQ5070) supported by the Natural Science Basis Research Plan of Shaanxi Province, China; Project (2017KJXX-27) supported by the Youth Science and Technology New Star Plan of Shaanxi Province, China; Project (3102017AX003) supported by the Fundamental Research Funds for the Central Universities, China
Corresponding author: Jiao LUO; Tel: +86-29-88460465; E-mail: luojiao@nwpu.edu.cn
DOI: 10.1016/S1003-6326(19)64940-X

