J. Cent. South Univ. Technol. (2011) 18: 1018-1023
DOI: 10.1007/s11771-011-0797-0
Analysis of complete plasticity assumption for solid circular shaft under pure torsion and calculation of shear stress
LIU Guang-lian(刘光连)1, HUANG Ming-hui(黄明辉)1, TAN Qing(谭青)1,
LI Xian-fang(李显方)2, LIU Zhen(刘振)1
1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;
2. School of Civil Engineering and Architecture, Central South University, Changsha 410083, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2011
Abstract: The distribution of shear stress on the cross-section of plastic metal solid circular shaft under pure torsion yielding, the applicability of complete plastic model assumption and the shear stress formula were researched. Based on the shear stress formula of circular shaft under pure torsion in elastic stage, the formula of torque in elastic stage and the definition of yield, it is obtained that the yielding stage of plastic metal shaft under pure torsion is only a surface phenomenon of torque-torsion angle relationship, and the distribution of shear stress is essentially different from that of tensile stress when yielding under uniaxial tension. The pure torsion platform-torsion angle and the shape of torque-torsion angle curve cannot change the distribution of shear stress on the shaft cross-section. The distribution of shear stress is still linear with the maximum shear stress τs. The complete plasticity model assumption is not in accordance with the actual situation of shaft under torsion. The experimental strength data of nine plastic metals are consistent with the calculated results of the new limiting strain energy strength theory (LSEST). The traditional yield stress formula for plastic shaft under torsion is reasonable. The shear stress formula based on the plane assumption in material mechanics is applicable for all loaded stages of torsion shaft.
Key words: pure torsion; yield; complete plastic model assumption; shear stress calculation; limiting strain energy strength theory
1 Introduction
For plastic metals in uniaxial tension or compression, the phenomenon that the strain on a cross-section increases with the relative stress in a constant state is defined as the yielding of materials in tension or compression. Some plastic metals also yield under pure torsion. According to the “ideal elastic-plastic model” and the “complete plastic model” assumption, the formula of relationship between the ultimate plastic torque and the maximum elastic torque of plastic metal shafts can be obtained [1-3]. In this work, based on the analysis and calculation of the yield torque and shear stress of shaft under pure torsion, it is proved that the “complete plastic model” assumption, with plastic metal shafts under pure torsion and yielding, is not reasonable; however, the distribution of yield shear stress on a cross-section subjects to the “ideal elastic-plastic model” and the distribution of shear stress is approximately the same as that in elastic stage. The shear stress formula of circular shaft during all the loaded stages based on material mechanics is applicable.
2 Calculation of torsion shear stress and torque of solid circular shaft
2.1 Formula of shear stress and torque in elastic stage
The shear stress formula in elastic stage was obtained according to the rigid plane assumption based on the geometric deformation relationship of circular shaft in torsion, the Hooke law of shear, and its static condition. The rigid plane assumption assumes that after deformation, the cross-section of the shaft stays in the same circle as before with radical linearity, and the distance between the two cross-sections keeps invariant. According to the static condition, the resultant torque of the shear stress on the cross-section of the shaft is equal to the external torque. The formula of the shear stress at point ρ away from the axis under pure torsion can be expressed as
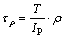 (1)
(1)
where τρ is the shear stress at point ρ from the axis of the cross-section, T is the torque, ρ is the distance between the acted point and the axis, IP=πR4/2 is the polar moment of inertia (R is the radius of the shaft).
When ρ=R, the maximum shear stress on the surface of the shaft can be expressed as
 (2)
(2)
where WP denotes the torsion cross section coefficient:
 (3)
(3)
According to Eqs.(1), (2) and (3), another formula of the shear stress can be obtained as
 (4)
(4)
Equations (1) and (4) are the formulas of shear stress on the cross-section of shaft during elastic stage under pure torsion. According to Eq.(4), and as shown in Fig.1(a), the distribution of shear stress on the cross-section of shaft is linear, the shear stress on the surface of the shaft is the maximum, and the shear stress on the axial centre is zero.
When the shear stress reaches the upper shear yield limitation, the torque loaded on the shaft is the elastic limiting torque. According to Eqs.(2) and (3), the elastic limiting torque TE can be obtained as
 (5)
(5)
where τsu is the upper shear yield.
2.2 Calculation of shear stress during elastic-plastic stage and strengthen stage
When the external torque exceeds the limitation of elastic torque, the plane assumption and the Hooke law are still assumed applicable [4]. HE et al [5] states “For circular shaft under torsion, the deformation law according to the plane assumption in material mechanics exists during the whole loading process, which has been fully validated by experiments and universally used in elastic plastic mechanics.” This result has been used universally in calculation of large deformation for plastic materials and torque for brittle materials [6-13]. In the national standards of Metallic Materials-Test at Room Temperature [14], the torsion strength of materials is calculated with Eq.(2); however, the experimental maximum torque is used in Eq.(2).
Based on the above results, under pure torsion, Eq.(2) can still be used to calculate the maximum shear stress of shaft in strengthening stage; Eq.(4) can still be used to calculate the relative distribution of shear stress.
2.3 Calculation of torque with two models in elastic- plastic stage
After the shaft reaches the elastic-plastic stage under torsion, it is assumed that the material of the shaft is ideal elastic-plastic. There are generally two assumptions of the distribution of shear stress in the elastic-plastic stage.
2.3.1 Formula of torque with ideal elastic-plastic model
As shown in Fig.1(b), the ideal elastic-plastic model assumes that the shear stress on a cross-section is a combination of linear distribution of shear stress and yield shear stress [1-3]. Take ρE as the radius of elastic region and τs as the yield shear stress, the resultant torque loaded on the cross-section of the shaft can be expressed as [1-2]
 (6)
(6)
2.3.2 Formula of torque with complete plasticity model
As shown in Fig.1(c), the complete plasticity model assumes that the shear stress on a cross-section is of uniform distribution of yield shear stress [1-4, 6]. When the radius of elastic region ρE=0 under ideal elastic-plastic assumption, it becomes the complete plasticity model.
From Eq.(6), the limiting plastic torque TP can be obtained as [1-2, 4, 6]
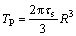 (7)
(7)
From Eqs.(5) and (7), the following equation can be obtained:
 (8)
(8)
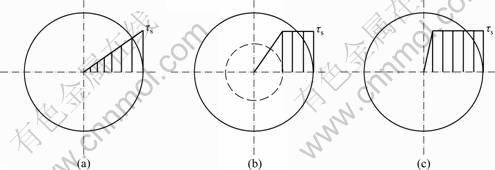
Fig.1 Three models of shear stress in plastic metal shaft under pure torsion: (a) Linear model; (b) Ideal elastic-plastic model; (c) Complete plasticity model
It can be obtained from experiment that the upper shear yield strength is approximately equal to the shear yield strength
 (9)
(9)
Substituting Eq.(9) into Eq.(8), the relationship between the limiting plastic torque TP and the maximum elastic torque TE can be obtained as [1-4, 6]
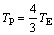 (10)
(10)
In another way as
 (11)
(11)
From Eq.(10), if the shear stress on the cross-section of solid shaft is equal to the yield shear stress and of uniform distribution with complete plasticity model, the loaded limiting plastic torque TP on the cross-section is 4/3 times of the maximum elastic torque that the shaft can bear. That is to say, considering the plasticity of materials, the bearing capacity of solid shaft rises by 33% under pure torsion [1]; or, the limiting plastic torque TP is 33% larger than the maximum elastic torque TE [2].
3 Analysis on shear stress and torque of solid shaft in elastic-plastic stage
3.1 Radius of elastic region and distribution of shear stress in pure torsion yielding stage of solid metal shaft
The phenomena of the deformation of the specimen increase notably with the external load on the specimen constant or approximately constant states when the load decreases is called yield. A typical yield torque-torsion angle curve of plastic metal shaft under pure torsion is shown in Fig.2, where OA denotes the elastic stage, and AB denotes the yield stage. From the torque-torsion angle curve based on experiment, after the torque has reached the yield stage AB, the exerted torque on shaft keeps at a constant approximately.
Assuming that the torsion yield stage of solid metal shaft obeys the ideal elastic-plastic model, according to Eqs.(5)-(6) and (9), the radius of the elastic region ρE can be obtained as
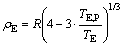 (12)
(12)
The elastic-plastic torque of plastic metal shaft during yielding stage under pure torsion is equal to the yield torque and also approximately equal to the maximum elastic torque:
 (13)
(13)

Fig.2 Torque-torsion curve of plastic metal shaft under pure torsion
Substituting Eq.(13) into Eq.(12), one can obtain
 (14)
(14)
According to Eq.(14), the radius of the elastic region is equal to the radius of the shaft theoretically under the ideal elastic-plastic model and the radical thickness of the surface plastic region is zero, which indicates that the shear stress on the cross section of the plastic metal is still linear distribution of the maximum shear stress τs, as shown in Fig.1(a).
Assuming that the shear stress on the cross section of shaft is uniform distribution of τa, as the acted torque on the shaft is the yield torque TS, the uniformly distributed shear stress τa can be obtained as
 (15)
(15)
According to Eq.(15), with the ideal elastic-plastic model, the shear stress on the cross section of the shaft becomes 3/4 times of the shear yield strength. The decrease of the shear stress will make the shaft detached from the yield condition. So, the shear stress on the cross section of the shaft cannot be uniformly distributed.
For a plastic metal with relatively long yield platform, the torque almost does not change even at the end of yield stage. From the above analysis, the shear stress on the cross-section of shaft is still approximately of linear distribution, and both formulas of shear stress in the elastic stage Eqs.(2) and (4) are also applicable. This also indicates that after entering the yielding stage under pure torsion, the distribution of shear stress on the cross-section of shaft is different from that of the torque-torsion angle. The torque-torsion curve reflects the changing of torque load and torsion angle during the torsion stage, the changing of torque load and torsion angle during the whole stage from the starting moment to the loading moment. Obviously, the torque-torsion curve from the starting moment to the loading moment is different from the shear stress distribution curve at the moment. The assumption by HE et al [11-13] that the distribution of shear stress at a certain loading moment is similar to the torque-torsion curve from the starting moment to the loading moment is worthwhile for further discussion.
3.2 Yield stress of plastic metal solid shaft under pure torsion
WANG and MA [15] proposed the experimental torsion yield stress formula of plastic shaft as τs=TE/WP, where TE denotes the maximum torque in the elastic stage, and the measured value of the yield torque in experiment is the limiting (plastic) torque TP. According to Eq.(11), the yield stress can be expressed as [15-16]
 (16)
(16)
The premise by WANG and MA [15] is that “the radius of the elastic region decreases with the increase of torque, and in limited condition, all the shear stress on the whole cross-section reaches the shear yield limitation”. According to the definition of yield, the increase of torque means that the shaft is not in yield condition. The measured yield torque in the experiment is the torque that keeps constant during a certain time, which reflects the actual value of yield torque. The experimental torsion device used now generally obtained the torque-torsion angle curve through data collection of computer and it is relatively easy to obtain the value of yield torque. During the experiment process with torsion loading, when the torque exceeds 4TE/3, there will not be yield platform, as shown in Fig.2. So, the premise by WANG and MA [15] that “the measured yield torque in experiment is the limiting (plastic) torque TP” is not reasonable, and their conclusion that “the coefficient in the experimental torsion yield stress formula of plastic shaft is 3/4” is also not reasonable.
3.3 Rationality analysis of complete plasticity model for shaft under pure torsion
According to Eq.(10), the limiting plastic torque of the shaft based on the complete plasticity model is 4/3 times of the maximum elastic torque. So, the shaft only obeys the complete plasticity model when the torque that the shaft bears is reached and is equal to 4TE/3.
From the sketch torque-torsion angle curve in Fig.2, assume that the axial of the shaft is ideal plastic material. When the torque exceeds TS, the distribution of shear stress on the cross-section of the shaft is of “ideal elastic-plastic model”. As the torque increases, the distribution of the yield stress on the direction of the radius on the cross-section of the shaft increases too. When the torque reaches 4TE/3, the shear stress on the whole cross-section is approximately of uniform distribution of the yield stress τs on the complete plasticity mode. Obviously, when the acted torque on shaft is larger than 4TE/3, the distribution of shear stress on the cross-section of shaft will certainly change, and it cannot still be uniform distribution.
From the previous analysis, the shear stress on the cross-section of the shaft in the yield stage is linearly distributed rather than equally distributed, which indicates that the shear stress at point B on the cross-section of the shaft is not uniformly distributed, so it is at point C. Based on the complete plasticity model, when the load under pure torsion exceeds TE and reaches 4TE/3, the distribution of shear stress on the cross-section turns gradually from linear distribution at point B to uniform distribution at point C, and will change after point C, which is obviously illogic and impossible. It is also in conflict with the assumption from other literatures that the shear stress on the cross-section of the shaft during the whole loading process under pure torsion is linearly distributed. Based on the above analysis, when the load reaches 4TE/3, the shear stress on the cross-section of the shaft is not equally distributed.
Under uniaxial tension, from the elastic stage to the yielding stage and before the necking stage, due to the equal transmission law of uniaxial tensile stress, the distribution of normal stress on the cross-section of the specimen at any constant is equal except for the neighborhood of the loading end. Under uniaxial tension, the external load and stress on the cross-section of the plastic metal specimen is nearly invariant when yielding; however, the strain changes when yielding. This is also a characteristic of uniaxial tensile yielding. From Eq.(4), in the elastic stage, the shear stress on the cross-section of shaft is of linear distribution proportional to the distance to the circle center rather than equal distribution. The previous analysis indicates however long the yielding platform is, the shear stress on the cross-section of shaft is still of linear distribution rather than uniform distribution when yielding, which is essentially from the phenomena that the stress on the cross-section of shaft is of equal distribution at any constant before the necking stage under uniaxial tension.
The torque cannot realize the equal distribution of shear stress in the shaft, and it cannot transform the linear distribution of shear stress into equal distribution even after entering the yielding stage. The limiting plastic torque formula Eq.(7) of solid shaft under pure torsion according to the complete plasticity model is just based on ideal assumption. From the above analysis, the assumption of complete plasticity model for shaft under pure torsion that “ the shear stress on a cross-section is equal to the yield shear stress and is of uniform distribution” is not consistent with the actual situation and completely different from the fact that the yield stress is of equal distribution under uniaxial tension, which is not practical in pure torsion. But the complete plasticity model is practically applicable in tension and compression.
4 Strength experiments of plastic metals and analysis of results
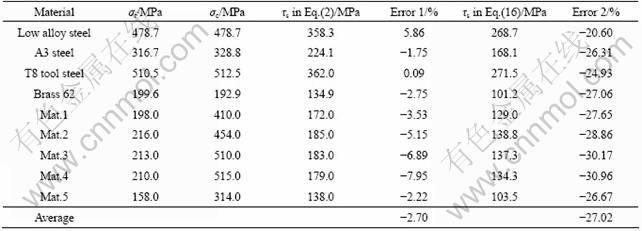
The values of tensile yield strength σt, compressive yield strength σc and torsion shear yield strength τs according to Eq.(2) of a low-alloy steel [16], A3 steel, T8 tool steel and brass 62 [17] are listed in Table 1. Assume that the tensile yield strength of the normal low alloying steel is equal to its compressive yield strength, as σt=|σc|. As early as 1955, KONJUSHKO conducted similar experiment with tool steel (Mat.1—Mat.5 in Table 1), and the experimental results are also listed in Table 1 [18].
LIU [17] proposed the limiting strain energy strength theory (LSEST), and the failure function can be expressed as
 (17)
(17)
where σt and σc denote the uniaxial tensile yield strength and uniaxial compressive yield strength for plastic materials and the uniaxial tensile limiting strength and uniaxial compressive limiting strength for brittle
materials, respectively. For convenience, we assume σt>0 and σc<0.
Theoretically, materials will fail when the value of failure function is equal to or larger than 1. The theoretical failure condition can be expressed as
fe(σ)≥1 (18)
The relative error of LSEST, according to Eqs.(17) and (18), is
 (19)
(19)
Based on the shear yield strength calculated according to Eqs.(2) and (16), respectively, relative error 1, relative error 2 and the average value according to the relative error equation of LSEST Eq.(19) are listed in Table 1. From Table 1, according to the traditional formula for torsion shear yield strength, the relative errors of nine plastic materials according to the new LSEST are all less than 10%, with an average relative error of -2.7%; and the relative error based on the calculated shear strength of WANG and MA [15], WANG et al [16] are -27.02%, which indicates the traditional method for calculating the yield shear stress of plastic metal shaft is consistent with the experimental results.
Under pure torsion, the failure of plastic materials is caused by the shear stress. The pure torsion stress is in a tensile-compressive principal stress state where the absolute value of the tensile stress and the compressive stress are equal. Based on LSEST, the relationship among the tensile yield strength σt, compressive yield strength σc, shear yield strength τs according to Eqs.(17) and (18) can be expressed as
 (20)
(20)
Table 1 Relative error of two methods calculating torsion yield stress
Equation (20) is the shear yield strength of LSEST according to the tensile yield strength and compressive yield strength.
Using Eq.(2), based on the experimental strength data of eight plastic metals (except low-alloying steel in Table 1 ), LIU [17] calculated the relative error between the theoretical shear yield strength and the torsion shear yield strength with LSEST, Mises strength theory, Tresca strength theory, respectively. The obtained average relative errors are 3.99%, -36.85%, and -27.08%, respectively. The LSEST demonstrates very good results. So, the traditional formula for calculating the yield shear stress of plastic metal shaft is reasonable. LSEST has also been applied to biaxial and triaxial strength calculation of concrete under various principal stress states [19].
5 Conclusions
1) When the torque loaded on the shaft exceeds the limiting elastic torque, the plane assumption and the Hooke law are still applicable.
2) Only a very thin layer of metal enters the plastic state in the yielding stage of plastic metal shaft under pure torsion. The platform-torsion angle cannot change the distribution of shear stress on the shaft cross-section and the distribution of shear stress is still linear with the maximum shear stress τs.
3) The torque-torsion angle curve cannot change the distribution of shear stress on the shaft cross-section. The traditional yield stress formula for plastic materials under torsion is still reasonable.
4) The complete plasticity model does not meet with the actual situation in pure torsion analysis of shaft and it is not practical.
References
[1] BI Ji-hong, WANG Hui. Engineering plastoelasticity [M]. Tianjin: Tianjin University Press, 2008: 143-146. (in Chinese)
[2] HIBBELER R C. Mechanics of materials [M]. 5th ed. New Jersey: Prentice Hall, 2003: 237-241.
[3] DING Da-jun. Engineering plastoelasticity [M]. Nanjing: Southeast Press, 2007: 78-80. (in Chinese)
[4] TIMOSHENKO S. Strength of materials (Part II): Advanced theory and problems [M]. 3rd ed. New York: Van Nostran Reinhold Company, 1978: 381-386.
[5] HE Yun-zeng, PAN Xin-ji. A method of testing the true stress-strain relationship of plastic materials through torsion test of solid circular shaft [J]. Technology Applications, 1987, 4: 40-47. (in Chinese)
[6] TIMOSHENKO S P, GERE J M. Mechanics of materials [M]. New York: Van Nostrand Reinhold Company, 1978: 100-103.
[7] WU P D,VAN DERGIESSEN E. Analysis of elastic-plastic torsion of circular bars at large strains [J]. Archive of Applied Mechanics, 1991, 61: 89-103.
[8] VAN DERGIESSEN E, WU P D,NEALE K W. On the effect of plastic spin on large strain elastic-plastic torsion of solid bars [J]. International Journal of Plasticity, 1992, 8: 773-801.
[9] HUANG S, KHAN AS, YAN H. Shear measurement using strain gages under large deformation and rotation [J]. Experimental Mechanics, 1993, 33: 55-58.
[10] LEE C S, HWANG W, PARK H C, HAN K S. Failure of carbon/epoxy composite tubes under combined axial and torsional loading: 1. Experimental results and prediction of biaxial strength by the use of neural networks [J]. Composites Science and Technology, 1999, 59: 1779-1788.
[11] HE Yun-zeng, ZOU Guang-ping. Determine finite-strain stress-strain relationship by torson test with cylindrical specimens [J]. Acta Mechanica Sinica, 2001, 33(6): 828-833. (in Chinese)
[12] HE Yun-zeng, ZOU Guang-ping. The concept and method for determining the constitutive law of materials by torson test with cylindrical specimens [J]. Journal of Experimental Mechanics, 2001, 6: 820-833. (in Chinese)
[13] YANG Li-hong, HE Yun-zeng, WU Guo-hui, ZOU Guang-ping. Analysis of large strain constitutive relationship based on torsion test [J]. Journal of Harbin Engineering University, 2006, 27(6): 816-820. (in Chinese)
[14] National Standards of the People’s Republic of China. Metallic Materials-Test at Room Temperature [S]. GB10128—88. 1989. (in Chinese)
[15] WANG Jun, MA Qing-jie. Analysis of stress to elastic and plastic torsion of element [J]. Journal of Jilin Institute of Chemical Technology, 2004, 21(2): 85-87. (in Chinese)
[16] WANG Mei-rong, FEN Wan-Li, LIU Rui-tang, LU Ying. Discussion on determination for torsion yield stress [J]. Journal of Mechanical Strength, 2007, 29(5): 870-872. (in Chinese)
[17] LIU Guang-lian. A novel limiting strain energy strength theory [J]. Trans Nonferrous Met Soc China, 2009, 19(6): 1651-1662.
[18] GOKHFELD D A, SADAKOV O S, KONONOV K M. On the ultimate strain criterion for fracture prediction at normal and elevated temperatures [J]. Dynamics, Strength & Wear-resistance of Machines, 1997, 3: 12-18.
[19] LIU Guang-lian, LIU Zhen, LI Xian-fang. Application research of limiting strain energy theory in strength calculation of concrete [C]// Proceeding of 2009 National Ph.D. Student Symposium on Civil Engineering. Changsha, 2009: 533-541. (in Chinese)
(Edited by PENG Chao-qun)
Received date: 2010-04-01; Accepted date: 2010-12-15
Corresponding author: LIU Guang-lian, PhD candidate; Tel: +86-731-88836906: E-mail: glliu@mail.csu.edu.cn