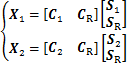DOI： 10.11817/j.issn.1672-7207.2020.06.010

基于CSP-PSO-SVM的运动想象EEG信号特征提取与分类算法

刘宝¹,唐雨琦^{1, 2},蔡梦迪¹,薄迎春¹,张月¹

（1. 中国石油大学（华东）信息与控制工程学院，山东 青岛,266580；

2. 中国电波传播研究所，山东 青岛,266109）

摘要:为了解决EEG信号特征提取困难及识别率低等问题，提出一种基于CSP-PSO-SVM的脑电(EEG)信号特征提取与分类算法。该算法首先通过小波包变换实现EEG信号的预处理，提取出EEG信号中的特定频段信号，然后通过构建“一对一”共空间滤波器对EEG信号进行特征提取，最后通过粒子群优化的支持向量机算法实现EEG信号分类识别，并选用2008BCI竞赛2A数据集进行算法分类效果校验。研究结果表明：改进型CSP-PSO-SVM算法的分类准确率最高可达到93.07%，且其平均准确率比其他算法的高。其特征能很好地反映EEG信号的特点，可明显提高分类识别的准确率，可为脑机接口的发展与应用提供参考。

关键词:运动想象；共空间模式；支持向量机；粒子群优化

中图分类号:TP241      文献标志码:A             开放科学(资源服务)标识码(OSID)

文章编号:1672-7207（2020）06-1551-14

EEG signal motion imagination feature extraction and classification algorithm based on CSP-PSO-SVM

LIU　Bao¹, TANG　Yuqi^{1, 2}, CAI　Mengdi¹, BO　Yingchun¹, ZHANG　Yue¹

(1. College of Information and Control Engineering, China University of Petroleum, Qingdao 266580, China；

2. China Research Institute of Radiowave Propagation, Qingdao 266109, China)

Abstract: In order to solve the problems of EEG signal feature extraction difficulty and low recognition rate, an EEG signal feature extraction and classification algorithm based on CSP-PSO-SVM was proposed. Firstly, the preprocessing and specific frequency band signal extraction of EEG signal was realized through wavelet packet transformation. Then, the feature of EEG signal was extracted by constructing a "one-to-one" common space filter. Finally, EEG signal classification and recognition were realized by the support vector machine algorithm optimized by particle swarm. The 2008BCI competition 2A data set was selected for algorithm classification effect verification. The results show that the improved CSP-PSO-SVM algorithm can achieve a classification accuracy of up to 93.07%, and the average accuracy is higher than that from other algorithms. The characteristics of EEG signals are well reflected by the proposed algorithm, the accuracy of classification and recognition is significantly improved, and it can provide a reference for the development and application of brain-computer interfaces.

Key words: motion imagining; common spatial pattern; support vector machine; particle swarm optimization

脑机接口(brain-computer interface，BCI)是一种直接通过外部设备与大脑建立连接通路的新型人机接口方式，包括信号采集，信号分析与外部设备控制3个部分^[1]。BCI分为植入式和非植入式，其中非植入式BCI采集的是大脑头皮的脑电信号(electro-encephalogram，EEG)，并且非植入式的采集方式有无损伤、使用便捷和成本低等优点^[2]，因此，基于EEG信号采集的BCI技术具有很好的研究价值，在医疗领域、人工智能领域和娱乐领域都具有广阔的应用前景。BCI技术中的核心环节就是对EEG信号进行分析处理，主要包括对于EEG信号的特征提取和识别分类^[3]。常用的EEG信号特征提取方法主要有时域分析法^[4]、频域分析法、时频混合分析法^[5]以及共空间模式(common spatial pattern，CSP)，其中以CSP的应用最广，效果也最好。CSP主要是利用矩阵对角化原理构建空间滤波器，然后通过滤波器提取信号中方差最优的特征。传统的CSP主要用于解决二分类问题，难以满足对EEG信号多分类的需求，因此，衍生了“一对一”CSP(pair-wise CSP，PW-CSP)^[6]以及“一对多”CSP(over versus rest CSP，OVR-CSP)^[7]。WU等^[7]在对OVR-CSP应用时得到了80%的平均准确率。除此之外，CHENG等^[8]提出了一种正则化CSP算法，并取得了较好效果。不过，虽然CSP具有良好的特征提取性能，但其在实际应用过程中仍存在对伪迹敏感度较高等问题，因此，依然无法满足现实中对EEG信号分类快速性与准确率的双重要求。常用的EEG信号分类算法主要有线性判别式(linear discriminant analysis，LDA)、神经网络算法(neural networks，NN)和支持向量机(support vector machine，SVM)。其中，LDA因为其判别函数是线性的，因此，对于不可分的特征向量线达不到理想的分类效果^[9]；神经网络算法可用于解决非线性问题，但其存在学习速率低、网络结构调整困难等问题；而SVM既能解决线性问题又可以解决非线性问题，对噪声具有鲁棒性，能很好解决非线性分类及小样本问题，并且在EEG分类问题中有较好的效果^[10]。SCHLOGL等^[11]基于EEG分类问题，将SVM与其他分类算法进行对比，发现其有较好的分类效果。但是，SVM参数调整的自适应性与快速性还有待进一步提高，以满足EEG信号分类识别中对实时性的要求。目前，对多类别EEG信号的特征提取依然十分困难，并且对EEG信号的分类识别也存在准确性较低等问题。为此，本文作者对EEG信号特征进行研究分析，提出一种基于CSP-PSO-SVM算法的EEG信号特征提取与分类算法，以提高EEG信号的特征提取准确性和分类效果；最后，采用2008年BCI竞赛的数据集2A对该算法进行验证。

1 EEG信号生理学基础

EEG信号图是指以从人的头皮表层采集到的电信号以电位作为纵轴，以时间作为横轴，所得到的电位与时间的相互关系平面图。由于人的大脑活动十分复杂，并且大脑各神经细胞的分布也不是均匀的，所以，由单个电极采集的EEG信号其实是大脑不同分区和各种类型的脑电波所叠加而成的信号。EEG信号具有频率、波幅和位相3个基本特征^[12]。在大脑进行不同的思维活动时，EEG信号的基本特征会产生相应变化。EEG信号是通过非植入式的BCI系统采集得到的，由于需要采集电极与头皮进行有效接触以采集EEG信号，因此电极的导联组合十分重要^[13]。目前，在EEG研究中电极安放通常采用国际脑电图学会标定的10-20电极导联定位标准，其中，10-20表示每个电极与邻近电极的距离为大脑垂直中心线(鼻根至枕外粗隆的前后连线)或水平中心线(左右耳廓UI高点之间的连线)的10%或20%。电极名称用电极位置所在的头部分区的英文单词首字母加上国际通用的阿拉伯数字来表示，如表1所示。表1中，以中心线为基准，左侧部位电极名称中的数字为奇数，右侧为偶数，正中位为零点(zero)，如A1和A2分别为左、右耳垂电极名称。接近中线用较小数字，较外侧用较大数字。10-20电极导联定位方法示意图如图1所示。

对不同刺激所产生的EEG信号的分析处理是目前的研究热点，不同的刺激也会产生不同的EEG信号特征，其中以对运动想象刺激所产生的EEG信号特征研究居多。由于通过人本身的运动想象刺激，诱发大脑感觉运动皮层的脑电发生节律性变化的特征较明显，可以通过对不同运动想象刺激下的EEG特征进行判别，以实现不依赖外部刺激的自发的外部设备控制，这具有一定的实际意义和研究价值，因此，运动想象EEG信号的分析研究及应用也成为了研究热点。本文对EEG信号特征提取与分类算法的研究也建立在对运动想象EEG信号特征的研究基础之上。

图1　10-20电极导联定位方法示意图

Fig. 1　Schematic diagram of 10-20 electrode lead positioning method

表1　10-20电极导联标准中不同部位的电极名称

Table 1　Electrode name for different parts in the 10-20 electrode lead standard

研究表明，当人主动进行肢体动作以及运动想象时，会激活大脑皮层EEG对应区域并改变EEG频带能量。与运动想象相关的频段为波、中间快波及波，即8~30 Hz，其中以8~12 Hz的节律以及18~26 Hz的节律为主。在大脑做单侧的运动或运动想象时，大脑同侧运动感知区节律和节律幅度会升高，即产生事件相关同步(event-related synchronization，ERS)现象，而对侧/节律幅度会降低，即出现事件相关去同步(event-related synchronization，ERD)现象^[14]。因此，ERD/ERS现象可以作为对运动想象信号进行识别的有效依据。本文主要针对想象左手、想象右手、想象舌头和想象脚这4类EEG信号进行分析和研究。

2 基于CSP-PSO-SVM的运动想象EEG信号特征提取与分类算法

为提高多类EEG信号识别准确率，通过对EEG信号特征的研究，提出一种基于CSP-PSO-SVM的特征提取与分类算法，该算法主要包括预处理、特征提取与分类3个部分，整体结构如图2所示。

图2　EEG信号特征提取及分类算法整体结构图

Fig. 2　Overall structure of EEG signal feature extraction and classification algorithm

该算法各部分的具体组成及处理流程如下。

1) 预处理部分。该部分首先提取EEG信号中的刺激反应区间信号，剔除数据中明显的干扰，然后利用小波包变换进行伪迹滤波以及EEG特征频段信号提取，最后按照一定的比例将实验数据分成测试数据与训练数据。

2) 特征提取部分。该部分首先利用训练数据构造多类“一对一”的CSP空间滤波器即“PW-CSP”滤波器。然后，将测试数据与训练数据通过“PW-CSP”滤波器进行滤波处理；最后，经过Hilbert变换和归一化处理得到最终的EEG数据特征。

3) 特征分类部分。该部分首先用训练数据对应的特征值输入SVM进行训练，且SVM的参数值由粒子群算法(particle swarm optimization，PSO)进行全局优化得到，然后用测试集的特征值对训练好的分类器进行精度测试。

2.1　基于小波包变换的EEG信号预处理

因为EEG信号很微弱且易受眼电、心电的伪迹干扰，需要对其进行预处理以去除伪迹与噪声。由于小波包变换具有无冗余、无疏漏优势，能实现对信号的局部时频分析，可以满足对包含大量细节成分的EEG信号的分析需求，并且无需考虑额外的眼电信号采集通道，因此，在对比各类预处理算法后，本文最终选择用小波包变换来实现特征频段的提取。

对EEG信号进行小波包变换其实可以视为通过选择一个形状可变且能做平移的信号分析窗即小波基函数对EEG信号进行扫描分析。小波包函数的表达式如下^[15]：

(1)

式中：u_n(t)为t时刻的信号在分解后的节点n处的表达式；为位移；和为1对共轭正交的小波包滤波器，满足。且当时，可得到尺度函数，小波基函数。

小波包变换是一个类似二叉树的结构。若将小波包分解中的节点标注为(其中为小波包分解的深度或者层数，为节点的频带顺序)，则在进行层小波包分解之后，第个节点所对应的频带范围为，其中，为采样频率。

对EEG信号进行小波包变换时，首先需要根据EEG信号的特征选择合适的小波基函数，然后需要确定EEG信号的特征频段，以确定小波包分解的层数与重构节点。

2.2　基于CSP-Hilbert变换的4类运动想象EEG信号特征提取

在对EEG信号进行预处理之后，需要对其进行特征提取。基于对EEG信号本身特征的研究与分析，本文提出基于CSP-Hilbert变换的特征提取算法，以提取出数据中归属于某一类别的特征分量。该算法主要包括一级特征提取单元、二级特征提取单元和终极特征提取单元3个部分。其中，一级特征提取单元由共空间模式算法构成，二级特征提取单元由Hilbert变换构成，终极特征提取单元由归一化和算数求和处理构成，具体流程如图3所示。

2.2.1　一级特征提取单元的算法原理　

此部分主要是利用CSP算法得到不同类别EEG信号的空间特征。CSP算法的主要思想是利用矩阵的对角化特征找到1个最优的空间因子，使得2类数据的方差值差异最大化，且类内的方差最小，该算法多用于EEG信号特征处理^[16-17]。假设X₁和X₂分别为2类N×T维的EEG数据(N为通道数，T为每通道的采样点数，且有N

(2)

式中：S₁和S₂分别为2类相互线性独立的源信号幅值；S_R为2种类型任务下所共同拥有的源信号幅值，C_R为与S_R相应的共有的空间模式；假设S₁和S₂分别由m₁和m₂个源所构成，则C₁和C₂便由S₁和S₂相关的m₁和m₂个共同空间模式组成。

由于每个空间模式都是1个N×1维的向量，下面用这个向量来表示单个的源信号所引起的信号在N个源即N个通道上的分布权重。CSP算法的目标是设计空间滤波器F₁和F₂得到空间因子W。经过CSP空间滤波的EEG数据可以表示为

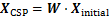(3)

式中：X_CSP为CSP空间滤波后所得到的EEG特征数据；X_initial为EEG原始信号幅值。

由原理可知CSP只能解决2类数据的分类问题，为了将多分类问题转化为二分类问题，多采用构建“一对一”或者“一对多”共空间滤波器即PW-CSP或者OVR-CSP滤波器，其中，PW-CSP滤波器效果相对较好，因此，本文中采用构建PW-CSP滤波器的方式进行特征提取。对于d类EEG数据，则需要建立[d(d-1)/2]组PW-CSP滤波器，每类对应其中(d－1)组滤波器。以4类EEG数据为例，需要分别构建6组PW-CSP滤波器，每一类对应其中的3组滤波器，如图4所示，其中， W₁~W₆为6个空间滤波器。

先以训练数据为数据输入，对4类EEG数据构建PW-CSP滤波器后，将训练数据和测试数据统一进行滤波处理即可分别得到训练数据和测试数据的一级空间特征。

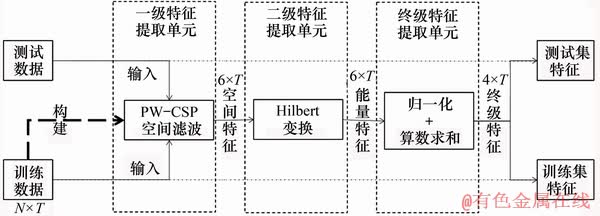
图3　EEG信号特征提取算法

Fig. 3　EEG signal feature extraction algorithm

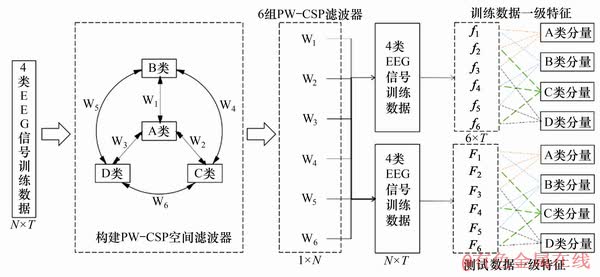
图4　一级特征提取单元示意图

Fig. 4　Schematic diagram of the 1st-level feature extraction unit

2.2.2　二级特征提取单元的算法原理　

一级特征提取单元提取到的是不同类别EEG信号的空间特征，但这些特征不能完全满足EEG信号的分类要求，因此，需要再进行下一步处理。根据帕斯维尔定理，信号时域总能量与频域总能量存在相等的关系，因此，可以通过Hilbert变换求取信号包络，即通过Hilbert变换将信号频域能量的变化转化为时域能量变化，将ERD\ERS现象映射到时域特征上。Hilbert变换可理解为将一个原始信号和另一个信号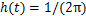做卷积的结果，其本质上是1个转向器，即将信号相位推迟90°。Hilbert变换也是研究ERD/ERS现象的重要手段，其表达式为

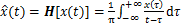(4)

式中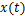：为原始信号幅值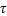；为时移变量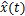；为原始信号的Hilbert变换结果。将经过第1部分处理之后的信号进行Hilbert变换，得到如式(4)所示的Hilbert变换输出，进而得到EEG信号在时域的二级能量特征。同样以4类EEG数据为例，其Hilbert变换过程如图5所示。

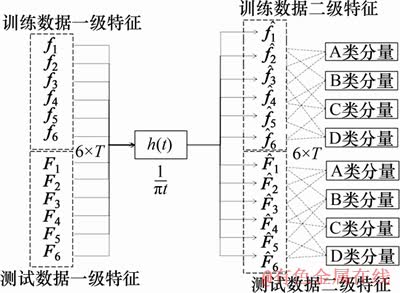
图5　二级特征提取单元示意图

Fig. 5　Schematic diagram of the 2nd-level feature extraction unit

2.2.3　终极特征提取单元的算法原理　

在经过前2个特征提取单元的处理之后，还需要进行归一化处理，以降低基线不稳、危机干扰对信号特征的影响。归一化处理是将信号以时间序列为基准，将信号幅值转化为0~1之间。同样以4类EEG数据为例，若某一时刻一组训练数据经过二级特征提取单元的处理之后得到的二级能量特征为6组向量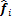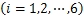，则其归一化处理为

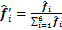(5)

式中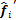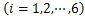：为归一化之后的最终特征。在归一化之后，对归属每一类的特征分量进行求和，即可得到最终的特征，如图6所示。

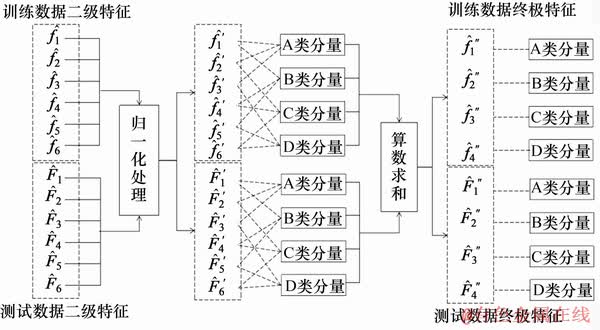
图6　终级特征提取单元示意图

Fig. 6　Schematic diagram of the final-level feature extraction unit

2.3　基于PSO-SVM的4类运动想象EEG信号分类算法

在获得EEG信号的特征之后，需要利用分类器进行分类识别。由于SVM能够解决机器学习中普遍存在的局部极值问题和高维度问题，并具有很强的泛化能力，同时，在解决小样本问题、非线性问题和模式识别问题等方面也有很好的效果，因此，本文采用SVM作为非线性EEG信号分类器。实践表明，SVM的性能与核函数类型及其参数选择以及支持向量机算法中的容忍度因子密切相关，因此，核函数的选择以及容忍度因子的参数调整十分重要。本文采用粒子群优化(particle swarm optimization，PSO)的方式对支持向量机中的参数选择进行优化调整并以交叉验证(cross validation，CV)的方式衡量算法的泛化能力，以提高算法的自适应性与快速性。

以SVM实现EEG信号特征分类识别的基本思想如下：首先通过1个核函数构成的非线性映射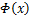将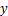类EEG信号特征映射到高维空间，然后找到1个超平面使得所有点到超平面的距离大于一定值^[18]，对最优超平面的构造归结为凸二次规划问题：

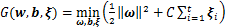
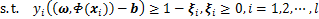(6)

式中：C为容忍度因子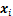；为EEG信号的特征向量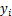；为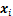所对应的类别；为构造的超平面的法向量；为超平面的偏置向量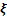；为松弛向量。

该凸二次规划问题可转换为对其对偶规划问题进行求解：

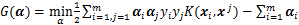
(7)

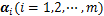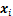式中：为核函数；为拉格朗日向量，若，则称对应EEG信号的特征向量为支持向量。对式(7)求解可得到最终的超平面和决策函数分别如式(8)和式(9)所示：

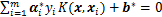(8)

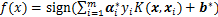(9)

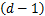由SVM原理可知，最后得到的决策函数为1个符号函数，因此，只能解决二分类的问题。而对于EEG信号识别这类多分类问题，通常采用直接法和间接法2种方法来求解。本文采用间接法中的“一对一”法(one-versus-one，OVO-SVMs)。OVO-SVMs通过在任意2类样本之间设计1个SVM分类器，对于d类EEG数据，则需要建立个SVM分类器，每类对应其中个SVM分类器，然后以投票法来确定样本最终类别，例如对于第1类和第2类的SVM分类器，若将信号输入判定为第1类，则第1类的票数加1，反之则第2类的票数加1。以44类EEG信号为例，SVM的设计与投票过程如图7所示，图7中SVM_i-j代表第i类和第j类之间的分类器。

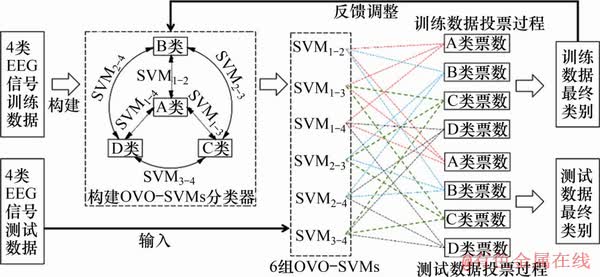
图7　SVM分类过程示意图

Fig. 7　Schematic diagram of SVM classification process

由于EEG信号具有非线性、高维度等特征，因此，本文选择映射维度不受限制的径向基函数(radial basis function，RBF)作为核函数，其表达式为

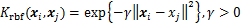(10)

由式(7)和式(10)可知：RBF核函数中的函数宽度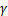以及SVM算法中的容错率因子C对于最终的模型建立极为重要，其直接决定SVM的性能。因此，需要找到(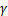，C)的最优参数以得到最佳SVM分类模型。对于参数(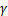，C)的优化确定，一般采用网格搜索或者经验法选取，但在算法训练速率上还有待提高，因此，本文采用PSO实现全局搜索优化。

PSO主要是来源于鸟类觅食的最优策略^[18]，对于SVM参数优化来说，鸟类觅食可以类比为对参数(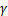，C)最优参数的寻找。首先将鸟抽象为没有质量和体积的粒子，并延伸到多维空间，即初始化一群随机粒子作为随机解。假设延伸至D维，某个粒子I在D维空间的位置表示为矢量X_i=(x₁,x₂,，x_D)，飞行速度表示为矢量V_i=(v₁，v₂，，v_D)。每个粒子都有一个目标函数决定的适应值(fitness value)，在每次迭代的飞行过程中积累自己的飞行经验来确定下一步运动。本文中的目标函数为以k-CV(k-folder cross-validation )方法进行交叉验证下的平均识别率。k-CV是将数据集分为k个子集，每个子集轮流作为一次验证集，其余作为训练集，进行k次训练验证，将k次验证的平均识别率作为最终的交叉验证识别率。

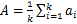(11)

式中：A为最终的交叉验证识别率；k为子集的数量；a_i为第i次的验证识别率。

可见，在由PSO优化的SVM参数选择中，是通过粒子跟踪发现的最佳参数(，C_best,m)和现在的位置X_m，计算出交叉验证识别率，然后更新找寻方向，如式(12)和式(13)所示。

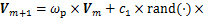
(12)

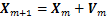(13)

式中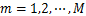：；M为算法迭代的次数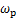；为惯性因子且非负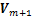；为粒子更新后的速度；V_m为粒子当前的速度；rand(·)为介于(0,1)之间的随机数；X_m+1为粒子更新后的位置；X_m为粒子的当前位置；c₁和c₂为学习因子。

整体的算法流程图如图8所示。由图8可知，算法可分为5步：

1) 读取样本数据，随机产生1组(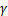，C)作为初始位置；

2) 把整个样本平均分割为k个互补包含的子集；

3) 根据当前的(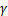，C)训练SVM计算识别交叉验证下的平均识别率，即计算k个子集轮流作为训练集，其余子集作为验证集时，依据所得到的k次验证识别率的平均值以及式(12)和式(13)更新位置。

① 初始化i=1；

② 子集留作检验集，其余子集合并起来作为训练集，训练SVM；

③ 计算i子集的准确率，直到i=k+1；

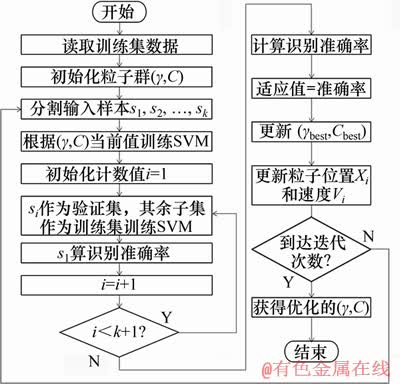
图8　PSO优化SVM参数算法流程图

Fig. 8　PSO optimized SVM parameter algorithm flow chart

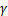4) 以交叉验证的平均识别率作为适应值，并记忆个体与群体所对应的最佳位置为(，C_best)，根据式(12)和式(13)搜寻更好的(，C)；

5) 重复步骤2)~4)，直到满足最大迭代次数为止。

3 实验结果对比分析

3.1　实验条件与数据来源

本文采用离线数据集对所提出的算法进行实验验证，包括3个步骤：EEG数据预处理、特征提取与识别分类。仿真计算机配置条件为：CPU，Intel(R) Core(TM) i5-5200U(2.20GHz)；RAM，8.0 GB；操作系统，Windows 10；仿真环境为MATLABR2018b。

采用2008年BCI竞赛中的标准4类运动想象EEG数据集2A^[19]来验证本文所设计的算法效果。该数据集EEG信号由22路Ag/AgCl电极测量，电极分布参照国际10-20导联标准。采集时以左乳头作为参考电位，右乳头作为地，采样频率为 250 Hz。共对9名被试(T01，T02，，T09)进行4类运动想象的试验，每个人进行2个独立周期的试验，每个周期记录288组数据，各类别72组。在仿真实验时，用其中一个周期的采集数据作为训练集，另一个周期的数据作为测试集。实验范例如图9所示，被试在每次试验的3~6 s的时间内进行运动想象。

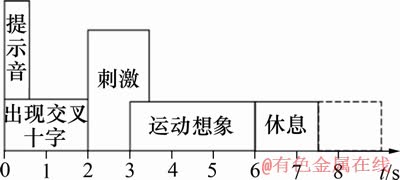
图9　试验范例定时方案

Fig. 9　Timing scheme of paradigm

3.2　4类运动想象EEG信号特征

当人进行运动想象时会出现ERD/ERS现象^[20]，因此，ERD/ERS可作为运动想象EEG信号的识别依据。但是，ERD/ERS现象并非出现在所有的频段。为了便于后期实验的特征提取，需要对ERD/ERS现象出现的频段进行研究。为此，本文绘制出被试T01的一组4类运动想象的对数功率谱密度以及其在频率为6.6，13.2，19.7和26.3 Hz的脑地形图，如图10所示。

由图10可见：ERD/ERS现象在频率为13.2，19.7和26.3 Hz时较明显。所以，ERD/ERS现象主要出现在波和波，并且由文献[21]可知EEG信号的频谱在9~13 Hz的变化最大。因此，在预处理时选择提取EEG中9~13 Hz频段的成分。

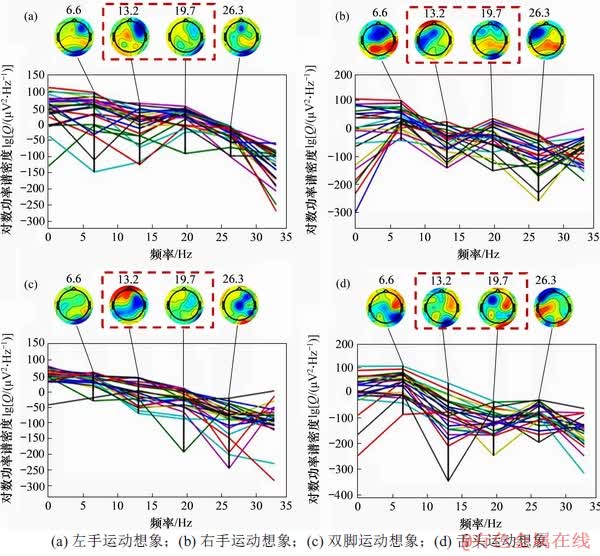
图10　4类运动想象对数功率谱密度

Fig. 10　Four types of motion imaginary logarithmic power spectral density

3.3　预处理结果与分析

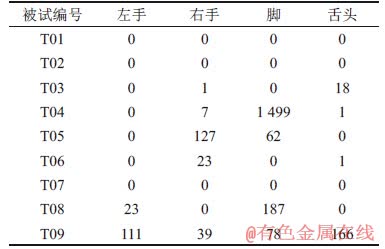
由于该实验数据为连续采集，因此，要先根据实验范例提取出刺激之后3 s反应时间内的EEG信号，在提取出之后发现实验数据中存在部分缺失值。9名被试的缺失值数量见表2，其中被试T04和被试T09的缺失值数量最多。由于缺失值会影响最后算法的实现效果，因此，本文采取均值插补的方式对缺失值进行处理。

表2　每名被试的4类运动想象EEG数据中的缺失值(NaN)数量

Table 2　Number of NaN values in EEG data for each subjects with four types of exercise imaginary    个

在处理EEG信号中的明显伪迹之后，可以依据提出的基于小波包变换预处理算法对EEG信号进行预处理。此处以被试T09的1组左手的运动想象EEG数据中C3通道的数据为例，首先采用快速傅里叶变换求取信号频率分布的方式对原始数据进行频谱分析。图11所示为该通道的原始信号时域波形与单边频谱图。由图11可见：原始信号时域波形杂乱无章，无法直观地看出信号特征，在频域中频率范围主要集中在30 Hz以内，而本文所需求的信号频段为9~13 Hz。因此，需要对其进行下一步处理。

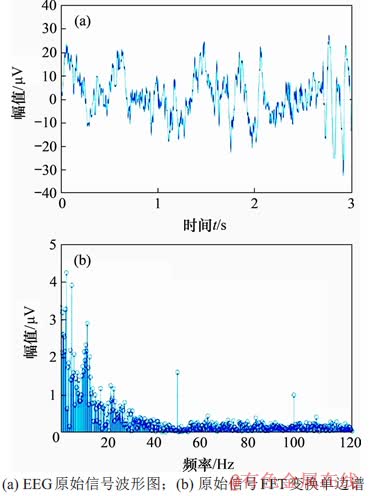
图11　原始信号时域波形与单边频谱图

Fig. 11　Original signal time domain waveform and unilateral spectrum

由于实验数据的采样频率均为250 Hz，且目标频率段为9~13 Hz。因此，本文采用较为常用的Daubechies小波基中的db6小波基函数对EEG信号进行6层分解，分解过程如图12所示。

图12　6层小波包分解示意图

Fig. 12　Diagram of 6-layer wavelet packet decomposition

为简化表达，假设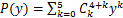，其中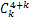，为二项式的系数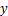，为转换函数，则db6的转换函数的平方为

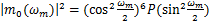(14)

式中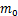：为转换函数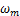；为转换值。可以发现，在经过6层分解之后所得到的第(6,4)和(6,7)这2个节点的频段分别为11.718 8~13.671 9 Hz和9.578 2~ 11.718 8 Hz，已满足对目标频段范围的要求。因此，选取第(6,4)和(6,7)这2个节点进行信号重构之后，再合成最终的信号。

重构信号时域波形与单边频谱图如图13所示。由图13可见：经过小波包变换后，可得到原始EEG信号中所需频段范围信号特征，并且所得信号在时域上的波形更光滑。

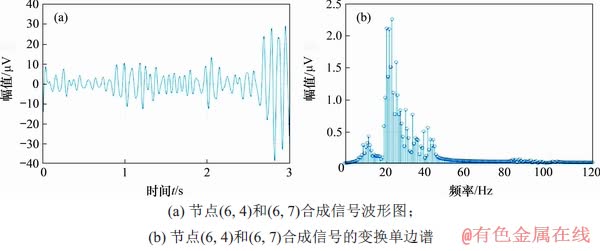
图13　节点(6, 4)和节点(6, 7)合成信号的时域波形图与单边频谱

Fig. 13　Time domain waveform and unilateral spectrum of composite signal of node (6, 4) and node (6, 7)

3.4　特征提取结果与分析

对预处理之后的数据，利用CSP-Hilbert变换进行特征提取实验，得到每一组EEG信号的终极EEG信号特征。并且由算法原理可知，终极特征向量是由该组EEG信号中归属于每一类的特征成分所构成。以被试T03的特征提取过程为例，在经过3层特征提取之后，得到了4×750维的特征向量，每一行即代表每一类的特征成分。表3所示为均等分布的8个采样点对应的特征值以及每一类特征分量之和。

表3　被试T03的部分特征值及其特征分量之和

Table 3　Some eigenvalues and the sum of characteristic components of subject T03

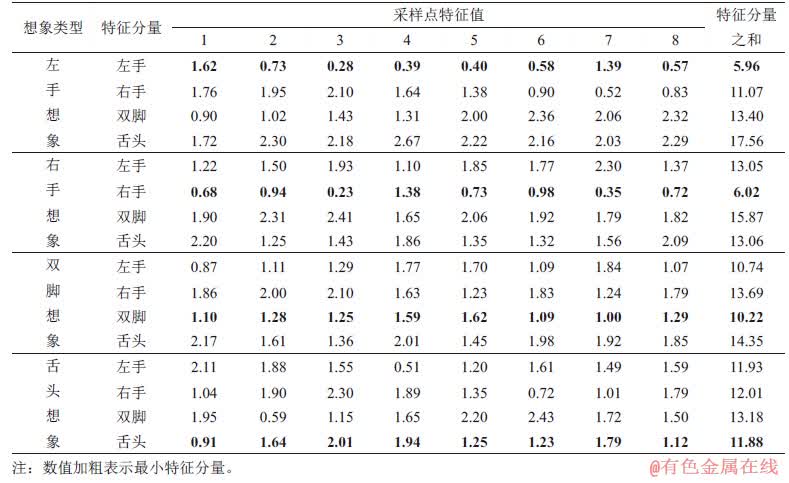
将被试T03的4类运动想象EEG信号特征以时间为横轴，相对幅值为纵轴，得到了被试T03特征分布图，如图14所示。由图14可以更直观地看出特征成分的分布关系。由表3和图14可知：信号特征中某类的特征分量中最小的分量与信号类别相对应。但是在具体应用时，会存在特征分量不足以进行区分的情况，比如有的信号存在最小的特征分量并不对应所属类别，因为其余特征分量在某一点存在远小于其他特征分量的极值点。因此，还需要引入分类器加以判别区分，进一步提高EEG信号分类识别的准确率。

3.5　分类结果与分析

本文采用基于PSO优化的SVM分类器进行分类识别。首先将4×750维的特征向量中的每一行进行算术求和，即得到一组4×1维的特征向量作为最终的输入特征。然后将训练集输入分类器中进行训练，得到每名被试的(，C_best)。PSO参数设置如表4所示。最终优化得到的每名被试的(，C_best)以及交叉验证识别率，如表5所示。图15所示为被试T03和T09训练时PSO的平均适应度。

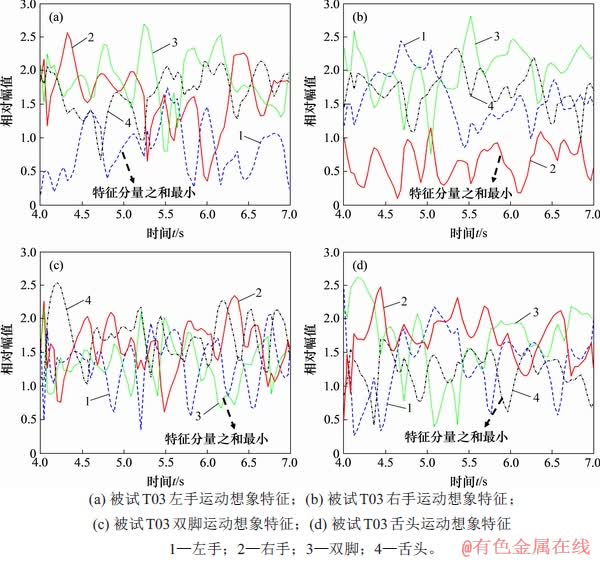
图14　被试T03的4类运动想象EEG信号特征

Fig. 14　Characteristics of four types of motion imagnation EEG signals of subject T03

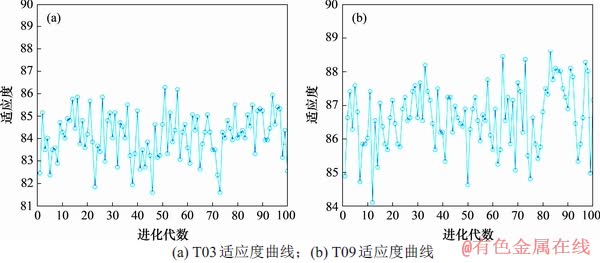
图15　PSO迭代优化适应度曲线

Fig. 15　PSO iterative optimization fitness curves

表4　PSO参数设置

Table 4　PSO parameter setting

表5　每名被试经PSO优化得到的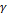_best和C_best

Table 5　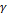_best and C_best optimized by PSO for each subject

在完成训练之后，将测试数据的特征向量输入SVM分类器进行分类。分类结果采用目前通用的Kappa系数K进行衡量：

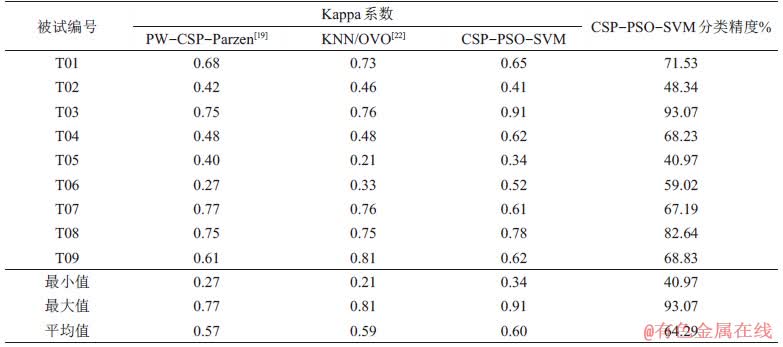
表6　本文算法与其他算法分类结果对比

Table 6　Comparison of classification results from the proposed algorithm and other algorithms

(15)

式中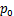：为准确率。Kappa系数越高，则对应的识别率越高。将本文提出的算法分类结果与BCI竞赛第1名算法分类结果^[19]及文献[22]中算法分类结果进行对比，结果如表6所示。由表6可知：在BCI竞赛中，第1名使用带通滤波器去除伪记进行预处理，再通过构建PW-CSP滤波提取特征，最后通过朴素贝叶斯Parzen窗口分类器进行分类，其分类结果的Kappa系数平均值为0.57，最大值为0.77，最小值为0.27；文献[22]采用KNN进行分类，其Kappa系数平均值为0.59，最大值为0.76，最小值为0.21；而本文采用的CSP-PSO-SVM方法所得Kappa系数平均值为0.60，最大值为0.91，最小值为0.34。由此可见，基于CSP-PSO-SVM的算法具有一定的优势。

4 结论

1) 提出了一种基于CSP-PSO-SVM的分类算法，该算法包括基于CSP-Hilbert变换的特征提取以及基于PSO优化的SVM算法的分类识别2部分。

2) 与其他算法相比，本文方法提高了EEG信号分类识别的准确率，最高可达到93.07%。

参考文献：

[1] CHEN Xiaogang, WANG Yijun, NAKANISHI M, et al. High-speed spelling with a noninvasive brain–computer interface[J]. Proceedings of the National Academy of Sciences of the United States of America, 2015, 112(44): 6058-6067.

[2] SHIN J W, KWON S B, BAK Y, et al. BCI induces apoptosis via generation of reactive oxygen species and activation of intrinsic mitochondrial pathway in H1299 lung cancer cells[J]. Science China Life Sciences, 2018, 61(10): 1243-1253.

[3] PFURTSCHELLER G, NEUPER C, GUGER C. Current trends in Graz brain-computer interface (BCI) research[J]. IEEE Transactions on Rehabilitation Engineering, 2000, 8(2): 216-219.

[4] 李松, 伏云发, 杨秋红, 等. 基于左右手运动想象单通道脑电信号的预处理研究[J]. 生物医学工程学杂志, 2016, 33(5): 862-866.

LI Song, FU Yunfa, YANG Qiuhong, et al. Pretreatment research based on left and right hand motor imagery for single-channel electroencephalogram[J]. Journal of Biomedical Engineering, 2016, 33(5): 862-866.

[5] 徐宝国, 宋爱国. 基于小波包变换和聚类分析的脑电信号识别方法[J]. 仪器仪表学报, 2009, 30(1): 25-28.

XU Baoguo, SONG Aiguo. EEG signal recognition method based on wavelet packet transform and clustering analysis[J]. Chinese Journal of Scientific Instrument, 2009, 30(1): 25-28.

[6] 徐鲁强, 肖光灿, 黎茂锋. 脑电信号共空间模式模糊融合的研究[J]. 生物医学工程学杂志, 2015, 32(6): 1173-1178.

XU Luqiang, XIAO Guangcan, LI Maofeng. Study on electroencephalogram recognition framework by common spatial pattern and fuzzy fusion[J]. Journal of Biomedical Engineering, 2015, 32(6): 1173-1178.

[7] WU Wei, GAO Xiaorong, GAO Shangkai. One-versus-the-rest(OVR) algorithm: an extension of common spatial patterns(CSP) algorithm to multi-class case[C]//2005 IEEE Engineering in Medicine and Biology 27th Annual Conference. Shanghai, China: IEEE, 2005: 2387-2390.

[8] CHENG Minmin, LU Zuhong, WANG Haixian. Regularized common spatial patterns with subject-to-subject transfer of EEG signals[J]. Cognitive Neurodynamics, 2017, 11(2): 173-181.

[9] TREDER M S, PORBADNIGK A K, SHAHBAZI AVARVAND F, et al. The LDA beamformer: optimal estimation of ERP source time series using linear discriminant analysis[J]. NeuroImage, 2016, 129: 279-291.

[10] CHEN Minyou, TAN Xuemin, LI Zhang. An iterative self-training support vector machine algorithm in brain-computer interfaces[J]. Intelligent Data Analysis, 2016, 20(1): 67-82.

[11] SCHLOGL A, LEE F, BISCHOF H, et al. Characterization of four-class motor imagery EEG data for the BCI-competition 2005[J]. Journal of Neural Engineering, 2005, 2(4): 14-22.

[12] SHARMA R, PACHORI R B. Classification of epileptic seizures in EEG signals based on phase space representation of intrinsic mode functions[J]. Expert Systems With Applications, 2015, 42(3): 1106-1117.

[13] ZHANG Yu, ZHOU Guoxu, JIN Jing, et al. Optimizing spatial patterns with sparse filter bands for motor-imagery based brain–computer interface[J]. Journal of Neuroscience Methods, 2015, 255: 85-91.

[14] 谢平, 齐孟松, 张园园, 等. 基于多生理信息及迁移学习的驾驶疲劳评估[J]. 仪器仪表学报, 2018, 39(10): 223-231.

XIE Ping, QI Mengsong, ZHANG Yuanyuan, et al. Driver fatigue assessment based on multi-physiological signals and transfer learning[J]. Chinese Journal of Scientific Instrument, 2018, 39(10): 223-231.

[15] 杨帮华, 颜国正, 严荣国. 脑机接口中基于小波包最优基的特征抽取[J]. 上海交通大学学报, 2005, 39(11): 1879-1882.

YANG Banghua, YAN Guozheng, YAN Rongguo. The feature extraction in brain-computer interface based on best basis of wavelet packet[J]. Journal of Shanghai Jiao Tong University, 2005, 39(11): 1879-1882.

[16] 张毅, 尹春林, 蔡军, 等. Bagging RCSP脑电特征提取算法[J]. 自动化学报, 2017, 43(11): 2044-2050.

ZHANG Yi, YIN Chunlin, CAI Jun, et al. Bagging RCSP algorithm for extracting EEG feature[J]. Acta Automatica Sinica, 2017, 43(11): 2044-2050.

[17] 徐鲁强, 肖光灿, 黎茂锋. 脑电信号共空间模式模糊融合的研究[J]. 生物医学工程学杂志, 2015, 32(6): 1173-1178.

XU Luqiang, XIAO Guangcan, LI Maofeng. Study on electroencephalogram recognition framework by common spatial pattern and fuzzy fusion[J]. Journal of Biomedical Engineering, 2015, 32(6): 1173-1178.

[18] XIAO Yancai, KANG Na, HONG Yi, et al. Misalignment fault diagnosis of DFWT based on IEMD energy entropy and PSO-SVM[J]. Entropy, 2017, 19(1): 6.

[19] BCI competition: download area[EB/OL]. [2008-07-03].http: //bbci.de/competition/iv/download.html.

[20] 赵丽, 李小芹, 边琰, 等. 多模式刺激下运动想象脑电信号的特征调制研究[J]. 生物医学工程学杂志, 2018, 35(3): 343-349.

ZHAO Li, LI Xiaoqin, BIAN Yan, et al. Study on feature modulation of electroencephalogram induced by motor imagery under multi-modal stimulation[J]. Journal of Biomedical Engineering, 2018, 35(3): 343-349.

[21] 施锦河, 沈继忠, 王攀. 四类运动想象脑电信号特征提取与分类算法[J]. 浙江大学学报(工学版), 2012, 46(2): 338-344.

SHI Jinhe, SHEN Jizhong, WANG Pan. Feature extraction and classification of four-class motor imagery EEG data[J]. Journal of Zhejiang University(Engineering Science), 2012, 46(2): 338-344.

[22] 刘冲, 颜世玉, 赵海滨, 等. 多类运动想象任务脑电信号的KNN分类研究[J]. 仪器仪表学报, 2012, 33(8): 1714-1720.

LIU Chong, YAN Shiyu, ZHAO Haibin, et al. Study on multi-class motor imagery EEG classification based on KNN[J]. Chinese Journal of Scientific Instrument, 2012, 33(8): 1714-1720.

（编辑 伍锦花）

收稿日期： 2019 -12 -21; 修回日期： 2020 -03 -28

基金项目(Foundation item)：中央高校基本科研业务费专项资金资助项目(20CX05006A)；国家自然科学基金资助项目(60775052)；中石油重大科技项目(ZD2019-183-007) (Project(20CX05006A) supported by the Fundamental Research Funds for the Central Universities; Project(60775052) supported by the National Natural Science Foundation of China; Project(ZD2019-183-007) supported by the Major Scientific and Technological Program of CNPC)

通信作者：刘宝，博士，教授，从事油气田智能检测和控制技术研究；E-mail：liubao@upc.edu.cn