一种改进的支持向量机增量学习算法
秦亮,唐静,史贤俊,肖支才
(海军航空工程学院 控制工程系,山东 烟台,264001)
摘要:为了解决支持向量机在处理大规模样本时存在的不足,研究了支持向量的性质;根据样本的空间分布规律,提出一种改进的支持向量机增量学习算法。这种学习方法以密度法为基础,结合距离判据,获得了样本向量的选拔因子。以选拔因子为基础设计一种增量学习算法,在减少重复学习样本的同时,尽可能保留样本空间信息,从而得到较高的训练精度和较快的训练速度。仿真实验验证该方法的有效性。
关键词:支持向量机;增量学习;支持向量
中图分类号:TP181 文献标志码:A 文章编号:1672-7207(2011)S1-0708-04
Improved incremental training algorithm of support vector machines
QIN Liang, TANG Jing, SHI Xian-jun, XIAO Zhi-cai
(Department of Control Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China)
Abstract: In order to figure out the deficiency of the SVM on extensive sample, the nature of SV was studied. An improved incremental training algorithm was put forward based on the dimensional of samples. A chosen gene factor gotten by density and distance criterion was used in this method. In this method the number of training samples is decreased and the space information is kept. So, the training speed is improved while the precision is not reduced. And the simulation proves the efficiency of this method.
Key words: support vector machine; incremental training; support vector
支持向量机是一种在统计学习理论基础上发展而成的一种新的机器学习方法,它遵循结构风险最小化的基本原则,具有很强的泛化能力,能较好地解决小样本、非线性、高维数及局部极小点等实际问题[1]。在故障诊断、模式识别及信号处理等领域得到了广泛的应用。但是,支持向量机也存在着不足与局限,其本身具有较高的时间复杂度和空间复杂度,并且在传统SVM中,所有的训练样本都是同等对待的,这样就增加了样本的训练复杂度,所以,支持向量机在处理大规模样本时会遇到一定困难。为解决这一问题,近年来,增量学习技术的引入逐渐成为一个研究的 热点。
增量学习技术是一种得到广泛应用的智能化数据挖掘与知识发现技术,可以分解支持向量机的空间复杂度,而且,在样本的训练过程中,通过支持向量的选择,降低核矩阵的复杂度,从而降低训练复杂度。Syed等[2]于1999年提出了这一思想。经过不断的研究,目前,发展比较成熟的增量学习算法主要包括基于分块的方法[3]和基于KKT条件的方法[4]。在此基础上,人们提出了许多改进方法,如在文献[5-6]中使用分层次的SVM分类器的方法,利用初级SVM的分类结果对新增样本进行划分。但这些算法必须保存全部历史样本,计算所需存储空间大大增加。文献[4,7]中提出的类似时间窗的算法,丢弃非SV样本以提高SVM的在线学习速度并减少对历史样本的存储,但这些丢弃方法缺乏新增样本对SV集影响的考虑,在丢弃的同时也导致分类知识的丢失,因为被丢弃的样本同样含有分类知识,甚至在后续学习过程中可能成为SV。
1 支持向量机的基本原理
设二分类问题的训练集为
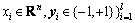 。其中,xi是第i个输入向量,yi是相应与xi的类标,l是样本数目。分类问题的目标是确定决策函数y(x)=sign(f(x)),函数f(x)具有如下的形式:
。其中,xi是第i个输入向量,yi是相应与xi的类标,l是样本数目。分类问题的目标是确定决策函数y(x)=sign(f(x)),函数f(x)具有如下的形式:
 (1)
(1)
式中: 为输入空间到特征空间的映射,系数向量w和偏差项b为待求量。未知量通过求解以下二次规划问题得到。
为输入空间到特征空间的映射,系数向量w和偏差项b为待求量。未知量通过求解以下二次规划问题得到。
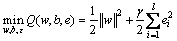 (2)
(2)
s.t

其拉格朗日函数为:
 (3)
(3)
其中: 为Lagrange乘子,式(3)的K-K-T条件为:
为Lagrange乘子,式(3)的K-K-T条件为:
 (4)
(4)
i=1,2,…,l
写成矩阵的形式为:
 (5)
(5)
其中: ,
, ,
, ,
, ,
,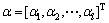 。
。
消去变量w和e,并结合Mercer条件,式(5)可写成
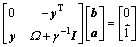 (6)
(6)
其中: 。令
。令 ,求解式(2),可得
,求解式(2),可得
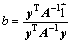 (7)
(7)
 (8)
(8)
由式(1)可知 ,分类函数可从下式得到
,分类函数可从下式得到
 。
。
2 改进的支持向量机增量学习算法
2.1 增量学习算法基本原理
新的增量学习算法基于以下2个基本原理。
原理1:设f(x)为SVM分类决策函数,{xi,yi}为新增样本。满足判别条件的新增样本将不会增加到SV集,违背判别条件的新增样本将使SV集发生变化。
违背KKT条件的样本可以分为3类:(1) 位于分类间隔中,与本类在分类边界同侧,可以被原分类器正确分类的样本,满足0≤yif(xi)<1;(2) 位于分类间隔中,与本类在分类边界异侧,被原分类器分类错误的样本,满足-1≤yif(xi)≤0;(3) 位于分类间隔外,与本类在分类间隔异侧,被原分类器分类错误的样本,满足yif(xi)≤-1。
原理2:新增样本违背KKT条件,则原样本集中非SV可能转化为SV。
此原理的证明可参见文献[8-9]。在增量学习中,只考虑新增样本和原来的SV集,虽然符合第一个基本原理,但是这样可能会丢失原来训练集中的信息,而且也不能十分有效地淘汰无用样本。
SVM增量学习中支持向量的变化是SVM从线性可分情况的最优分类面发展而来的。最优分类决策函数为:
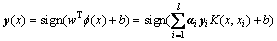 (9)
(9)
2.2 算法思想
在增量学习算法的研究中,已经提出了多种新增样本的筛选方法,但在这些方法中,对于原样本的非SV,大都是简单地抛弃,从而忽视了非SV在新的分类函数下转化为SV的可能性,造成分类信息的丢失。包括新增样本集中满足KKT条件和原样本集中非SV的样本,必须采取有效的方法淘汰无用样本,保留重要信息。SV从几何意义上来说,就是两类样本中距离最优分类面最近的样本。本文作者采用密度聚类与距离判别相结合的方法确定要保留的样本,与增量样本组合成新的样本集重新进行训练。
考虑到在一般情况下普通样本集中,支持向量或潜在的支持向量的数目要远小于非支持向量的数目,所以,可以认为,支持向量距离类中心比较远,且周围一定范围内的同类样本数量比较小。因此,如果将一个样本周围一定范围内同类样本的数量定义为样本密度,则样本密度从一定程度上反映了此样本在整个样本集合中的相对位置情况。在此基础上,廖东平等[9]提出从样本密度的角度选取边界向量,这种方法可以提取边界向量,但是与最优分类面距离较远的边界向量,即数据群另一面的边界向量也被提取出来。所以,应该应用距离判据进行区分。
本文作者将以样本密度和距离判别相结合,根据模糊数学的相关理论,定义了一种选拔因子,并以此为基础确定边界向量,进入新的学习样本集,在不显著增加计算复杂度的前提下,最大限度地保留了原始样本的特征。
定义样本点的密度度量为不超过距离阈值的样本数量:
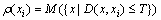 (10)
(10)
其中,距离使用Minkowsky定义,即
 (11)
(11)
式中:l为样本的位数;λ为正整数,λ=2时的距离为Euclidean距离。
选拔因子为:
 (12)
(12)
其中:
 (13)
(13)
式中: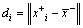 为样本到另一类的中心向量的距离,
为样本到另一类的中心向量的距离, 为两类中心的距离。
为两类中心的距离。
3 算法描述
输入:初始训练样本集A,增量样本集B。
输出: 上的分类器ψ和支持向量SV。
上的分类器ψ和支持向量SV。
(1) 使用标准的支持向量机学习算法在样本集A上进行学习,得到分类器ψA,支持向量集SVA;
(2) 计算样本集A中向量的选拔因子;
(3) 构造工作集B′,B′为B中所有违反ψA所定义的KKT条件的样本;
(4) 如果B′=Φ,转至步骤(7);
(5) 如果B′≠Φ,以B′与A中选拔因子大于ε的样本组成新的样本集,得到分类器ψA,支持向量机SVA;
(6) 返回步骤(1),重复执行;
(7) 输出 上的分类器ψ和支持向量SV。
上的分类器ψ和支持向量SV。
需要说明的是,如果初始分类大于两个,也就是说样本集不仅有A和B,本学习算法可以继续学习下去,直至得到整个样本集上的最终分类器。
4 仿真分析
依据上面提出的算法,针对某型导弹测试数据集进行实验,共有1 325个样本,样本维数为26,样本类型包括故障和正常两种,其中初始训练样本取450个,并将剩余样本随机分为3组,构成3个增量学习样本集,仿真结果如表1所示。
从表1中可以看出,在初始训练阶段,2种算法速度和训练样本数相等,但是,在增量样本阶段,由于改进算法减少了迭代次数和训练样本的存储,训练速度大幅增加,同时因为采用了选拔机制,保持了分类精度的稳定。
表1 测试数据增量学习结果
Table 1 Results of incremental learning on test data

参考文献:
[1] 郭振凯, 宋召青, 毛剑琴. 一种改进的在线最小二乘支持向量机回归算法[J]. 控制与决策, 2009, 24(1): 145-148.
GUO Zhen-kai, SONG Zhao-qing, MAO Jian-qin. An improved online least squares support vector machines regression algorithm[J]. Control and Decision, 2009, 24(1): 145-148.
[2] Syed N A, Liu H, Sung K K. Incremental learning with support vector machines[C]//Proceedings of Workshop on Support Vector Machines at the International Joint Conference on Artificial Intelligence. Stockholm, 1999: 272-276.
[3] Syed N, Liu H, Sung K. Incremental learning with support vector machines[C]//Proceeding of IJCAI Conference. Sweden, 1999.
[4] 周伟达, 张莉, 焦李成. 支持向量机推广能力分析[J]. 电子学报, 2001, 29(5): 590-594.
ZHOU Wei-da, ZHANG Li, JIAO Li-chen. An analysis of SVMs generalization performance[J]. Acta Electronica Sinica, 2001, 29(5): 590-594.
[5] An J L, Wang Z G, Ma Z P. An incremental learning algorithm for support vector machine[C]//Proceedings of the 2nd International Conference on Machine Learning and Cybernetics. Xi’an, 2003: 1153-1156.
[6] Li Z W, Zhang J P, Yang J. A heuristic algorithm to incremental support vector machine learning[C]//Proceedings of the 3rd International Conference on Machine Learning and Cybernetics. Shanghai, 2004: 1764-1767.
[7] 张浩然, 汪晓东. 回归最小二乘支持向量机的增量和在线式学习算法[J]. 计算机学报, 2006, 29(3): 400-406.
ZHANG Hao-ran, WANG Xiao-dong. Incremental and on line learning algorithm for regression least squares support vector machine[J]. Chinese Journal of Computers, 2006, 29(3): 400-406.
[8] 曾文华, 马健. 一种新的支持向量机增量学习算法[J]. 厦门大学学报: 自然科学版, 2002, 41(6): 687-691.
ZENG Wen-hua, MA Jian. A novel approach to incremental SVM learning algorithm[J]. Journal of Xiamen University: Natural Science, 2002, 41(6): 687-691.
[9] 廖东平, 魏玺章, 黎湘, 等. 一种支持向量机增量学习淘汰算法[J]. 国防科技大学学报, 2007, 29(3): 65-68.
LIAO Dong-ping, WEI Xi-zhang, LI Xiang, et al. A removing for incremental support vector machine learning[J]. Journal of National University of Defense Technology, 2007, 29(3): 65-68.
(编辑 陈卫萍)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:国家自然科学基金资助项目(61074053)
通信作者:秦亮(1984-),男,山东潍坊人,博士研究生,从事自动测试技术及故障诊断方法研究;电话:13583552300;E-mail: qinliang982@163.com