Trans. Nonferrous Met. Soc. China 24(2014) 2964-2968

Evaluation of effect of viscosity changes on bubble size in a mechanical flotation cell

Wei ZHANG^1,2

1. Mining & Mineral Resources Division, Department of Business Administration, Chinalco China Copper Corporation Limited, Beijing 100082, China;

2. Department of Mining and Materials Engineering, McGill University, Montreal, QC, H3A 0C5, Canada

Received 9 September 2013; accepted 20 January 2014

Abstract: In operating flotation plants, the viscosity of the pulp can vary significantly. Consequently, the resulting impact on bubble size is of interest as many plants experience seasonal changes in water temperature, or particle size changes as ore hardness, mineralogy and throughput fluctuate. However, given its importance in flotation, there existed no mathematical relationship linking bubble size created in flotation machines to the key process variable of fluid viscosity. In this study, a program of investigation to develop such a model was utilizing a pilot-scale mechanical flotation machine, to investigate the effect of water viscosity due to temperature on bubble size distribution. The bubble sizes were determined using a specific bubble viewer and imaging technology. The temperature itself was varied as a method for introducing significant viscosity change. The viscosity-temperature effect introduced a correspondingly significant change in the water viscosity (1619 to 641 μPa·s). It is suggested that a considerably stronger relationship may exist, yielding D₃₂ versus (μ/μ₂₀)^0.776, and hence viscosity becomes an important design consideration for plants operating where pulp temperature fluctuations, very small particles or high solid fractions are present.

Key words: flotation; bubble size; viscosity; surface tension; frother

1 Introduction

Froth flotation widely utilises differences in physicochemical surface properties of various minerals to achieve specific separation [1]. The efficiency of this separation process is dependent on the size of the bubbles [1-5]. Therefore, the ability to control the generation of bubbles in order to produce an optimum size range in flotation cells is attractive. Towards this purpose, bubble size measurements and modelling in flotation cells are clearly required. There has been some work on bubble size measurements and modelling in flotation [6,7]; however, neither of them have been adequate in accounting for the effect of the key variables such as fluid viscosity affecting the flotation process.

Plants also operate in conditions where the pulp temperatures can vary from near 0 °C to near 70 °C, and particle size and solid content are in a wide range, which will impact pulp viscosity. As a result, the effective viscosity of the liquid/solid phase can vary greatly. Testing for the effect of viscosity change is not straightforward, and early experiments are focused on finding a suitable additive to alter the water viscosity without impacting the other properties [8]. Two materials were tried: sucrose (sugar) solution and polyacrylamide (PAM), a well-know thickening and flocculating agent [9-11]. The sucrose was proved to have some frothing properties and so was rejected on the basis that it could impact bubble size apart from viscosity effects. The PAM seemed to promise initially having a wide range in viscosity possible ((1-5)×10³ μPa·s), until at higher concentrations (0.15% in mass fraction and above) its impact on the D₃₂ was proved to be inversely dependent on time and concentration [5]. It is speculated that the long, cross-linked acrylamide chains were broken apart by the high shear in the impeller region of the Denver cell where the initial testing occurred. An attempt was therefore made to include the effect of viscosity on bubble size, by varying water temperature between 3 °C and 40 °C. The plan of work did not involve solids so the reference here to the effect of viscosity must be strictly that resulting from changes in water temperature. The ranges selected for all the variables can be considered representative of industrial practice, with some extension above and below typical operating range for frother concentration, and below normal for gas rate (J_g), in order to more fully define relationships. The initial work reported here was performed using the two phase water-gas (air) system in the laboratory environment. Once developed, the approach calls for an additional stage of experimentation by introducing solids as well.

2 Apparatus and method

2.1 Viscosity measurement

The viscosity measurement involved measuring liquid viscosity at different temperatures, as described in Fig. 1, in order to provide practical viscosity ranges (viscosity–temperature curve) for testing in the flotation machines. The setup consisted of a Canon-Fenske Routine (CFR) viscometer (size 100), a 6 L beaker, a thermometer, a magnetic stirrer, and a heating element connected to a thermocouple with a temperature sensor.

Fig. 1 Setup of viscosity measurement apparatus

The heating element was connected to the thermocouple which was set at the desired temperature. Based on the signal from the temperature sensor, the thermocouple regulates the heating of the element. If the set temperature is reached, the thermocouple will turn the heater off. The magnetic stirrer served to distribute the heat from the element evenly throughout the bath.

2.2 Bubble size determination

An AutoCAD sketch of the set-up to measure bubble size is shown in Fig. 2. The nominal volume of the Metso RCS^TM 0.8 m³ mechanical flotation cell is 800 L, with a standard test volume of 700 L employed. The impeller diameter is 21 cm and that of the outside diffuser is 33 cm. A feature of the design is the baffle ring at 40 cm from the bottom of the tank (32 cm below water surface) which divides the turbulent zone around the impeller from the quiescent zone above where bubble size is determined. The cell was forced-air and air supply was from a compressed air system and manipulated via a 400 LPM KMS^TM mass flow meter. The sampling tube of the MBSA was positioned 33 cm from the central shaft (19 cm from the wall) and 52 cm from the bottom of the tank (20 cm below the water surface). This location inside the quiescent zone had been established previously as both being representative of the average air rate in the cell and giving reproducible data [5,12,13]. All experiments were run under the following conditions: air superficial velocity (J_g, i.e., volumetric air rate divided by cell cross-sectional area) 1 cm/s and impeller speed 1500 r/min (equivalent to 5.73 m/s tip speed). The cell was filled with Montreal tap water and frother DF250 was added at 5×10^-6 (CCCx of 59%). The CCCx was set at a level where changes to D₃₂ would be evident [14].

Fig. 2 Side view of Metso RCS^TM 0.8 m³ mechanical cell and MBSA (CAD drawing)

In order to vary water temperature in the Metso cell as a mean of altering viscosity, the testing period was in winter and a test range of 3 °C to 40 °C was possible by varying proportions of cold and warmer water and by running the cell at the highest possible speed to generate additional heating. A total of five test series (i.e. 32 tests) were run to cover the full temperature range. Bubble sizes were determined using a specific bubble viewing chamber and sampling-for-imaging technique [15,16]. Further details were given in Refs. [13,17].

3 Results and discussion

Varying only viscosity without significantly affecting the many other factors that could influence bubble size is not straightforward. The point could be argued that other properties of water that are temperature-dependent could impacting the bubble size distribution, such as surface tension, density or contained enthalpy. The trends in Fig. 3 suggest that water temperature was selected as the first situational variable to test as a large change in viscosity occurs relative to the small changes in water surface tension and water density across the range of interest (3 °C to 40 °C). Inverse enthalpy appears overly sensitive to temperature and could be a variable affecting viscosity through molecular excitation. The relative change in viscosity does seem to tend well with relative D₃₂. It is proposed that one can reasonably conclude that viscosity is the water property most closely corrected with D₃₂ with changing temperature.

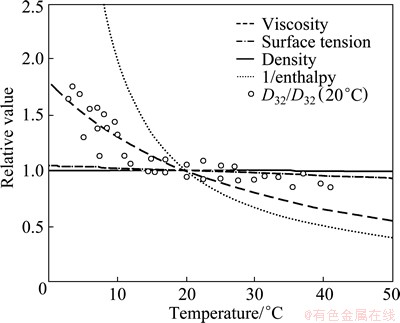
Fig. 3 Relative values for water of density, surface tension, viscosity and inverse enthalpy to their values at 20 °C as a function of temperature [5] (relative D₃₂ test data also were plotted)

The experiments were carried out in the Metso 0.8 m³ RCS pilot cell. Tests were run in 3 temperature ranges on separate days. Ice water was used from 3 °C to 9.5 °C (water warming over time); available tap water temperature ranged from 7 °C to 30 °C (temperature rise due to the liquid agitation by the impeller); hot water temperature ranged from 41 °C to 31.5 °C (water cooling over time). The results for D₃₂ and D₁₀ are shown in Figs. 4(a) and (b), respectively. Figure 4 shows that the D₃₂ and D₁₀ values increase markedly below about 10 °C, followed by a slower decline at higher temperatures.

The question then naturally arises as to how these relationships are compared to the change in water viscosity with temperature. Figure 5 shows the relationship between water temperature and viscosity (where μ is the viscosity at the temperature of interest and μ₂₀ is the viscosity at 20 °C). These measurements were made using the setup including Canon-Fenske Routine (CFR) viscometer, as described in Fig. 1. The similarity of this calibration curve with the bubble size-temperature curves of Figs. 4(a) and (b) is immediately obvious.

According to the relationship in Fig. 5, μ can be determined for temperature (t, °C) from (fitted from standard reference data)

      (1)

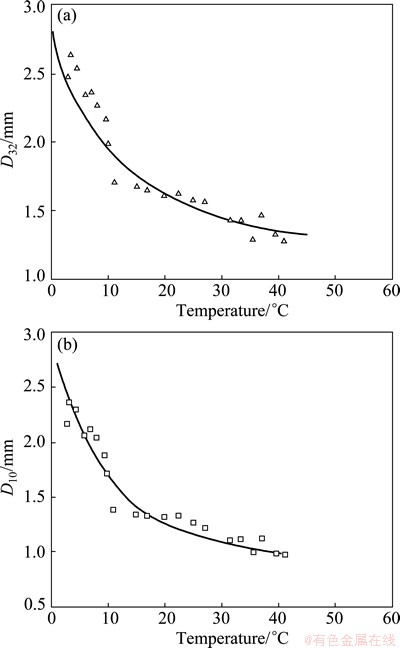
Fig. 4 Effect of water temperature on D₃₂ (a) and D₁₀ (b) at J_g =1.0 cm/s and 5×10^-6 DF250

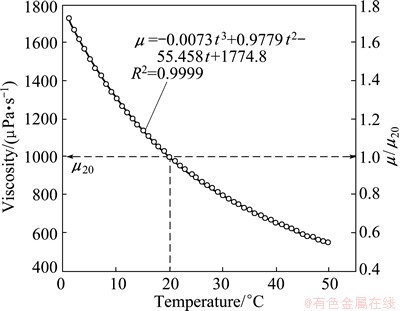
Fig. 5 Water viscosity versus temperature

Combining the data of Figs. 4(a) and 5, one obtains the comparison shown in Fig. 6. Noting the similarity of the curves, as noted earlier (Fig. 3), the variation in surface tension and density are very minor in comparison, so the inescapable conclusion must be that it is viscosity that affects the change in bubble size as no other property of the water is changed.

This observation, as seen in Fig. 6, has results in the following equation to characterize the D₃₂-viscosity relationship:

                        (2)

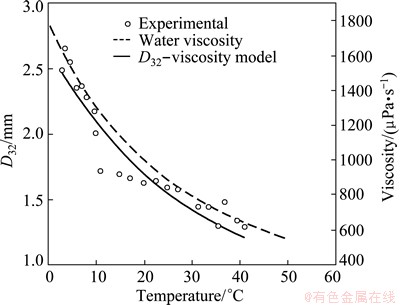
Fig. 6 Effect of water temperature on viscosity and D₃₂ for Metso cell

where D₃₂ is the Sauter mean diameter, μ is the viscosity at the temperature of interest, and μ₂₀ is the viscosity at 20 °C.

Table 1 indicates the measures of precision and goodness-of-fit for Eq. (2). An 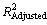 of 0.880 is acceptable for model-fitting; however, the 95% confident interval of ±0.27 mm is higher than the precision for the other variables tested [18]. The data and equation (Eq. (2)) along with upper and lower 95% confidence limits are shown in Fig. 7. Overall, Eq. (2) for D₃₂ mirrors the viscosity change with temperature reasonably well. However, the data do flatten in the range of 10-20 °C, contributing to the poorer overall precision of the data fit. Note that two data points well outside the 95% confidence limits were excluded from the data analysis. The effect of higher temperature (i.e. >50 °C) on frother activity is not known and it could well be that some effectiveness is lost due to volatilization as temperatures climb into 30 °C and above. The 1.662 mm value in Eq. (2) represents the data-fit value for D₃₂ at 20 °C. The viscosity-ratio term and exponent can be used in building the overall D₃₂ model to account for viscosity effects on D₃₂ in other than 20 °C conditions.

As noted, no specific references quantifying viscosity effects on the flotation performance of forced-air mechanical flotation cells could be located. However, the model can be used to investigate the impact on flotation performance of typical changes by assuming that a change in bubble size will produce a proportional (inverse) effect on S_b and hence mineral flotation rate constant k. The viscosity effect of interest is that for water viscosity at 5 °C representative of a typical summer-winter fluctuation (a 15 °C change) in plant process, water temperature is in a Canadian or non-tropical location. The bubble size model predicts, using Eq. (2), that water viscosity increases at 5 °C, and the D₃₂ increases to 1.38 mm, resulting in a rate constant decrease to 0.109 min^-1, and a corresponding recovery loss of 2.4%. Therefore, the D₃₂ model has been used to demonstrate that the impact of pulp (i.e. water) viscosity changes (for example, to summer-winter temperature fluctuations) can be substantial, and needs to be accounted for during plant operation and at the circuit design stage.

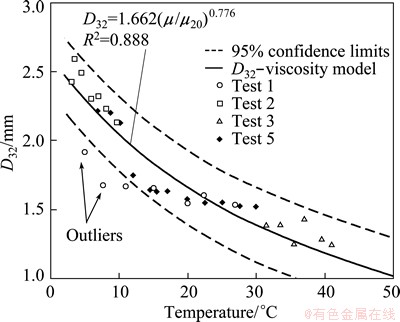
Fig. 7 Corresponding best-fit equation for D₃₂-viscosity model

Table 1 Measure of precision and goodness-of-fit for D₃₂-viscosity model presented in Fig. 7 and Eq. (2)

4 Conclusions

1) A detailed methodology was successfully developed for the measurement of viscosity and the establishment of viscosity-temperature curve for liquid.

2) The effect of viscosity was established by temperature variation of the water in the test flotation cell, covering the range of 3-40 °C, and showed that liquid viscosity has a significant impact on bubble size. The D₃₂ increases proportionally as (μ/μ₂₀)^0.776 developed here has been shown to be robust across a wide range of operating conditions, indicating that viscosity becomes an important design consideration for plants operating where pulp temperature fluctuations, very small particles or high solid fractions are present.

3) This work concerned itself with identifying the viscosity effect in the two-phase system, recognizing that increasing solid content and decreasing particle size will also impact fluid viscosity in a three-phase system. Some additional validation and calibration work for confirming that the two-phase model is an appropriate model for three-phase systems will be on the agenda.

Acknowledgments

Funding was through the Chair in Mineral Processing at McGill University, under the Collaborative Research and Development Program of NSERC (Natural Sciences and Engineering Research Council of Canada) with industrial sponsorship from Vale, Teck Cominco, Xstrata Process Support, Agnico-Eagle, Shell Canada, Barrick Gold, COREM, SGS Lakefield Research and Flottec.

References

[1] RAO S R, LEJA J. Surface chemistry of froth flotation [M]. 2nd ed. New York/London: Kluwer Academic Publication/Plenum Publishers, 2004.

[2] ZHANG W, ZHOU X, FINCH J A. Determining independent control of dual-frother systems–gas holdup, bubble size and water overflow rate [J]. Minerals Engineering, 2012, 39: 106-116.

[3] DOBBY G S, FINCH J A. Particle collection in columns-gas rate and bubble size effects [J]. Canadian Metallurgy Quarterly, 1986, 25(1): 9-13.

[4] YANG C, XU C, MU X, ZHOU K. Bubble size estimation using interfacial morphological information for mineral flotation process monitoring [J]. Transactions of Nonferrous Metals Society of China, 2009, 19: 694-699.

[5] NESSET J E, ZHANG W, FINCH J A. A benchmarking tool for assessing flotation cell performance [C]//Proceedings of 44th Annual Meeting of the Canadian Mineral Processors (CIM). Ottawa, ON, Canada: Canada Institute of Mining, Metallurgy and Petroleum, 2012: 183-209.

[6] LIZAMA H M, CARRION J, ESTRELLA D. Improvements in column flotation through the use of microcell spargers at Antamina [C]//Proceedings of 40th Annual Meeting of Canadian Mineral Processors (CIM). Ottawa, ON, Canada: Canada Institute of Mining, Metallurgy and Petroleum, 2008: 363-376.

[7] KRACHT W, FINCH J A. Bubble break-up and the role of frother and salt [J]. International Journal of Mineral Processing, 2009, 92 (3-4): 153-161.

[8] JAMES C J, MULCAHY D E, STEEL B J. Viscometer calibration standards: Viscosities of water between 0 °C and 60 °C and of selected aqueous sucrose solutions at 25 °C from measurements with a flared capillary viscometer [J]. Journal of Physics D: Applied Physics, 1984, 17: 225-230.

[9] TOSHIYUKI S, WATANABE M, FUKANO T. Effects of viscosity on coalescence of a bubble upon impact with a free surface [J]. Chemical Engineering Science, 2005, 60: 5372-5384.

[10] BEATTIE D A, HUYNH L, KAGGWA G B N, RALSTON J. The effect of polysaccharides and polyacrylamides on the depression of talc and flotation of sulphide minerals [j]. Minerals Engineering, 2006, 19: 598-608.

[11] CHAGAS B S, MACHADO D L P, HAAG R B, SOUZA C R, LUCAS E F. Evaluation of hydrophobically associated polyacrylamide-containing aqueous fluids and their potential use in petroleum recovery [J]. Journal of Applied Polymer Science, 2004, 91: 3686-3692.

[12] NESSET J E, FINCH J A, GOMEZ C O. Operating variables affecting the bubble size in forced-air mechanical flotation machines [C]//Proceedings of Ninth Mill Operators’ Conference. Fremantle, WA: The Australasian Institute of Mining and Metallurgy, 2007: 19-21.

[13] ZHANG W, NESSET J E, RAO S R, FINCH J A. Characterizing frothers through critical coalescence concentration (CCC95)- hydrophilic-lipophilic balance (HLB) [J]. Minerals, 2012, 2(3): 208-227.

[14] ZHANG W, ZHU S, FINCH J A. Frother partitioning in dual-frother systems: development of analytical technique [J]. International Journal of Mineral Processing, 2013, 119: 75-82.

[15] ZHANG W, KOLAHDOOZAN M, NESSET J E, FINCH J A. Use of frother with sampling-for-imaging bubble sizing technique [J]. Minerals Engineering, 2009, 22(5): 513-515.

[16] ZHANG W, NESSET J E, FINCH J A. Water recovery and bubble surface area flux in flotation [J]. Canadian Metallurgical Quarterly, 2010, 49(4): 353-362.

[17] ZHANG W, NESSET J E, FINCH J A. A novel approach to prevent bubble coalescence during measurement of bubble size in flotation [J]. Journal of Central South University, 2014, 21: 338-343.

[18] NESSET J E. Modeling the Sauther mean bubble diameter in mechanical, forced-air flotation machines [D]. Montreal: McGill University, 2011.

使用半工业化机械浮选机评估矿浆黏度变化对浮选气泡大小的影响

张 炜^1,2

1. 中铝中国铜业有限公司 企业管理部 矿产资源处，北京 100082；

2. 加拿大麦吉尔大学 采矿与材料工程系，蒙特利尔 H3A 0C5

摘  要：浮选过程中矿浆的黏稠度是由矿浆温度、矿粒浓度、矿粒细度等决定，它对浮选效率的影响一直受到工业界的极大重视。在实际生产中，一些自然因素和操作参数的变化，如季节性温度的浮动，矿石硬度、矿石性质的变化等产生的矿浆黏稠度的浮动，导致气泡尺寸和分布规律产生浮动，进而使选矿回收率等经济指标下滑。即便如此，在科研中矿浆黏稠度的相关研究并未受到重视。本研究的重点是黏稠度和气泡尺寸在浮选过程中的关系。试验采用半工业化美卓700 L机械浮选机和McGill大学独有的气泡观测仓，通过调整液体温度来改变黏稠度，在充分屏蔽其他浮选操作条件的情况下形成了气泡-黏稠度的关系图。结果显示了气泡尺寸D₃₂和黏稠度(μ/μ₂₀)之间呈现0.776的指数关系，有较强的关联性。本研究结果对实际生产中通过控制黏稠度来优化气泡尺寸，乃至浮选经济指标具有借鉴意义。

关键词：浮选；气泡尺寸；黏度；表面张力；起泡剂

(Edited by Hua YANG)

Corresponding author: Wei ZHANG; Tel: +86-13521508736; E-mail: zhang_wei@chalco.com.cn

DOI: 10.1016/S1003-6326(14)63432-4