基于免疫遗传算法改进DFNN模型及其应用

李彦斌¹，李存斌¹，杨尚东²

(1. 华北电力大学 工商管理学院，北京，102206；

2. 国网北京经济技术研究院，北京，100761)

摘  要：针对动态模糊神经网络(DFNN)在进行预测应用时容易陷入“局部极值”的缺陷，提出一种改进方案。综合人工免疫算法和遗传算法的优点，用免疫选择优化遗传算法的进化策略，提出一种新的免疫遗传算法。将免疫遗传算法对模糊神经网络的学习算法进行改进，增强其学习能力和算法的稳定性。结合复杂性强的短期电价预测问题，采集美国PJM电力市场的实际数据作为样本数据，对免疫遗传算法改进DFNN进行实证研究。研究结果表明：与DFNN的预测结果相比，改进后的方法在同样的运算条件下，预测精度提高4.5%，而运算时间仅增加6.4 s，说明基于免疫遗传算法对DFNN模型的改进效果较好。

关键词：免疫算法；遗传算法；动态模糊神经网络

中图分类号：TP18; TM74        文献标识码：A         文章编号：1672-7207(2008)02-0345-05

A new DFNN improved by artificial immune-genetic hybrid algorithm and its application

LI Yan-bin¹, LI Cun-bin¹, YANG Shang-dong²

(1. School of Business Administration, North China Electric Power University, Beijing 102206, China;

2. State Power Economic Research Institute, Beijing 100761, China)

Abstract: An improvement for dynamic fuzzy neural network (DFNN) was presented to avoid its running into the local extreme. By integrating the excellence of the artificial immune algorithm and the genetic algorithm, an new artificial immune-genetic hybrid algorithm was proposed, and its evolution game of the genetic algorithm was optimized by the immune algorithm. The artificial immune-genetic hybrid algorithm was used to improve the learning tactic and the steadiness of the DFNN. Based on the actual electricity price data of the American PJM power market, the proposed algorithm and the DFNN were applied in the complex problem of short-term electricity price forecasting. The comparison results indicate that the precision of the proposed algorithm is enhanced by 4.5% and the time is only increased by 6.4 s, so the improved effect of the proposed method is obvious.

Key words: artificial immune algorithm; genetic algorithm; DFNN

随着计算机科学的发展，人工神经网络方法得到了广泛应用。对于复杂、非线性系统预测问题，顾庆雯等^[1-2]将神经网络方法应用于电价预测问题，取得了较好的预测效果。与普通的人工神经网络相比，DFNN网络能够处理更多的影响因素^[3]。然而，DFNN网络的学习算法大多是基于BP学习算法，因而也存在容易陷入“局部极值”的结构性缺陷^[4]。为此，一些研究者提出了模糊神经网络的改进方法^[5-6]，通过优化模糊神经网络的网络参数或者改进模糊神经网络的学习算法。实践结果表明，改进模糊神经网络的学习算法效果更明显^[5-6]。在此，提出一种改进模糊预测方法，即先通过免疫选择提高遗传算法的全局搜索能力，再将改进后的遗传算法优化动态模糊神经网络的BP学习算法，得到基于免疫遗传算法优化的模糊神经网络短期电价预测模型。用该模型编制的Matlab仿真程序应用于波动性强、影响因素复杂的短期电价预测，结合美国PJM电力市场实际数据对该算法进行研究。

1  动态模糊神经网络(DFNN)模型

现有模糊神经网络的主要缺点是多数不具备反馈结构而使应用范围限于静态问题，对暂态问题控制无效^[7-9]。在实际生产过程中，对象常常具有动态特性，过程的变量是时间的函数，因此，研究具有动态特性的模糊神经网络更具有实际意义。通过在模糊神经网络内部引入递归环节，构成DFNN，DFNN的各个参数具有明确的物理意义，可以根据所计算的输入参数及对应的数据对DFNN网络进行有导师学习，完成模糊系统的参数辨识任务。它是一个动态映射网络，比普通神经网络更适于描述动态系统。

DFNN的拓扑结构如图1所示，它由5个部分组成：输入层L₁，模糊化层L₂，规则层L₃，归一化层L₄，输出层L₅。在第2层引入了递归神经元，由于递归神经元有内部反馈连接，因而可以获得系统的动态响应，能简化网络模型。在以下描述中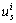，表示第s层的第i个节点的输入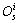，表示第s层的第i个节点的输出，s为网络的层数。

图1  DFNN神经网络结构

Fig.1  Structure of DFNN

第1层为输入层L₁，各个节点直接与输入向量各分量x_i相连，并将各输入值传到下一层。

其中：n为输入变量的个数；i=1, 2, …, n。

第2层为模糊化加递归层，每个节点代表1个语言变量值，如负大、零、正小等。它计算各输入分量属于各语言变量模糊集合的隶属函数(采用高斯    函数)：

此层中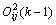记录了网络第(k-1)时刻的信息，因而可实现动态映射。

第3层为规则层L₃，每个节点代表1条模糊规则，用来匹配模糊规则的前件，完成模糊与操作计算出每条规则的适用度。

第4层为归一化层，节点与第3层的相同，实现归一化运算，为：

第5层为输出层，实现清晰化计算，得到输出值：

2 免疫选择遗传算法

遗传算法(GA)是一种模拟自然选择和进化过程的寻优算法，传统遗传算法在显示其巨大优越性的同时，也暴露出一些局限性，如传统遗传算法在接近全局最优解时搜索速度变慢，甚至陷入局部最优解^[10-12]。利用免疫系统的抗体多样性的遗传机理和细胞选择机理，可以有效改进和提高遗传算法的能力。在遗传算法中引入免疫的概念，用局部信息来介入全局寻优过程，抑制搜索过程中的重复现象，从而克服交叉和变异操作中的退化现象。

可用2个免疫操作来优化遗传算法：免疫接种；免疫选择^[13]。

2.1  免疫接种

假设个体P，免疫接种的意思是基于先前的信息在某些位上修改基因来最大限度地获得较高适应度。假设一个群体为C=(P₁, P₂, …, P_n)，在群体C上的免疫接种操作个体是从先前知识按比例选择而来的，即。这个操作是从先前的知识中抽象出来的。

2.2  免疫选择

这个操作由2步完成：

a. 检查抗生物。若后代比父辈的适应度小，则表示在交叉变异时出现了严重的基因损坏，这样就将父辈进行下一次竞争。

b. 退火选择^[10]：从先前的后代中选择个体时引入概率：

其中：f(P_i)为个体P_i的适应度；{T_k}为温度控制序列，趋于0。

2.3  免疫遗传算法(IG)具体步骤

免疫遗传算法的基本步骤如下：

a. 种群初始化。

b. 计算适应度，若满足迭代终止条件，则算法停止，输出最优结果。否则执行步骤c.。

c. 根据适应度以一定方式执行选择操作(这里采用轮盘赌选择)，并使用最佳个体保留策略。

d. 对种群实行交叉和变异操作。

e. 对种群进行疫苗接种。

f. 免疫选择操作，得到新一代父本。

g. 判断算法终止条件是否满足，若满足，则停止并输出最优结果；否则，返回执行步骤c.。

3  基于免疫遗传改进模糊神经网络的模型

DFNN的学习算法是基于BP方法的梯度方法，其偏重于局部搜索，缺乏全局搜索能力，通常容易陷入局部极值。这样，在训练后得到的往往是局部极值，而不是全局极值，而且网络训练的效果与网络的初始设置关系紧密。而免疫遗传算法算法则是在结合了遗传算法和免疫选择的优点基础上形成的全局性更强的优化算法，因而更能够搜索到全局最小值。本文设计的改进模糊神经网络，结合免疫遗传算法和BP算法的优点，全局参数通过免疫遗传算法来获得，局部的则通过BP算法来实现。这样，免疫遗传算法算法被当作模糊神经系统的离线训练控制器，BP算法则被当作在线训练控制器。通过整合这2种方法提出的新算法在学习能力和算法的稳定性方面都比其他算法有明显提高。所提出的免疫遗传算法改进模糊神经网络模型结构示意图见图2。

图2  IGDFNN模型结构示意图

Fig.2  Structure of IGDFNN

4  免疫遗传模糊神经网络用于短期电价预测的实验验证

4.1  环境设定

将提出的免疫遗传模糊神经网络应用于波动性强、受复杂规律影响的短期电价预测问题，其中预测模型和指标参考文献[14-15]。运用2007-08-15至2007-09-30美国PJM电力市场24 h真实电价数据为样本数据，其中用2007-08-15至2007-09-10的数据用作训练数据，2007-09-10至2007-09-28的数据用作检验数据，预测2007-09-29和2007-09-30当天  24 h节点电价。

算法实现预测的计算机软件平台为Windows XP2系统，硬件环境为Intel Core(TM)2 1.83 GHz，物理内存为1,024.00 MB。基于以上实证研究环境设定，将本文提出的免疫遗传算法改进DFNN预测模型(IGDFNN)与遗传算法改进DFNN预测模型(GDFNN)和DFNN预测模型进行实例分析，并对其实验结果进行比较。

4.2 结果比较

图3所示为免疫遗传算法改进DFNN算法(IGDFNN)，遗传算法改进DFNN算法(GDFNN)和DFNN的学习误差曲线对比结果。由图3可见，IGDFNN算法的误差曲线平缓，并且当训练结束时，误差较低，说明通过引入免疫遗传算法，提高了神经网络模型的学习能力，从而使训练误差更低。

1—IGDFNN; 2—GDFNN; 3—DFNN

图3  IGDFNN, GDFNN和DFNNＹ网络训练误差对比

Fig.3  Training error curves comparison among IGDFNN, GDFNN and DFNN

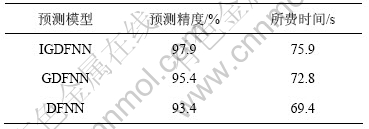
图4和表1所示为IGDFNN，GDFNN和DFNN预测电价与真实民价的对比结果。由图4可以看出，IGDFNN预测曲线比GDFNN预测曲线更加接近真实电价曲线，说明通过引入免疫遗传算法，改进了DFNN模型预测效果。由表1可以看出，改进前、后预测的时间成本大致相同，说明引入免疫遗传算法改进后的DFNN模型在提高预测精度的同时保证了预测效率。

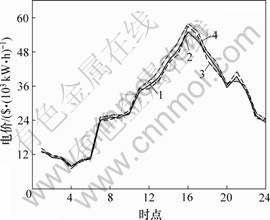
1—真实电价; 2—IGDFNN预测电价;

3—GDFNN预测电价; 4—DFNN预测电价

图4  IGDFNN, GDFNN和DFNN预测电价与真实电价对比

Fig.4  Comparison between forecasting results with IGDFNN, GDFNN and DFNN and real electricity price

表1  IGDFNN, GDFNN 和 DFNN预测结果对比

Table 1  Forecasting results comparison among IGDFNN, GDFNN and DFNN

5  结 论

a. 与单纯的遗传算法相比，引入免疫选择提高了遗传算法的全局优化能力。

b. 改进后的模糊神经网络预测效果得到较大提高，能够更好地适应波动性强、具有复杂影响因素的非线性预测问题。

c. 对电价的预测模型需考虑更多的相关因素，并且针对这些因素对电价波动产生的影响进行综合和比较，在此基础上，建立更客观、合理的电价预测模型。

参考文献：

[1] 顾庆雯, 陈 刚, 朱蕾蕾, 等. 基于遗传算法和径向基函数神经网络的短期边际电价预测[J]. 电网技术, 2006, 30(7): 18-21.
GU Qing-wen, CHEN Gang, ZHU Lei-lei, et al. Short-term marginal price forecasting based on genetic algorithm and radial basis function neural network[J]. Power System Technology, 2006, 30(7): 18-21.

[2] 张春辉, 闵 勇, 丁仁杰, 等. 级联相关的神经网络模型在边际电价预测中的应用[J]. 电力系统自动化, 2003, 27(3): 28-30.
ZHANG Chun-hui, MIN Yong, DING Ren-jie, et al. Application of the cascaded correlation network to forecast the marginal clearing price in power market[J]. Automation of Electric Power Systems, 2003, 27(3): 28-30.

[3] 彭春华. 电力市场短期边际电价的分时重构混沌相空间预测[J]. 中国电机工程学报, 2005, 25(23): 80-85.
PENG Chun-hua. Electricity market short-term marginal price forecasting based on period clustering restructure chaotic’s phase space[J]. Proceeding of the CSEE, 2005, 25(23): 80-85.

[4] TANG Shao-cheng, LI Han-xiong, CHEN Guan-rong. Adaptive fuzzy decentralized control for a class of large scale nonlinear systems[J]. IEEE Trans on Systems, Man and Cybernetics, 2004, 34(1): 770-775.

[5] 达飞鹏, 宋文忠. 基于模糊神经网络滑模控制器的一类非线性系统自适应控制[J]. 中国电机工程学报, 2002, 22(5): 78-83.
DA Fei-peng, SONG Wen-zhong. Adaptive control for a class of nonlinear system based on FNNSMC[J]. Proceedings of the CSEE, 2002, 22(5): 78-83.

[6] Yam H Y, ShahidehPour S M, Li Z. Adaptive short-term electricity price forecasting using artificial neural networks in the restructured power markets[J]. Electrical Power and Energy Systems, 2004, 26(8): 571-581.

[7] YANG Shang-dong, LI Xiang. A new ANN optimized by improved PSO algorithm combined with chaos and its application in short-term load forecasting[C]//Proceeding of the 2006 International Conference on Computational Intelligence and Security. Guangzhou, 2006: 945-949.

[8] 于金霞, 蔡自兴, 邹小兵, 等. 基于神经网络辨识的移动机器人航向误差校准方法[J]. 中南大学学报: 自然科学版, 2005, 36(5): 745-750.
YU Jin-xia, CAI Zi-xing, ZOU Xiao-bing, et al. Calibration method for heading error of mobile robot based on neural networks identification[J]. Journal of Central South University: Natural Science, 2005, 36(5): 745-750.

[9] 周富强, 曹建国, 张 杰, 等. 基于神经网络的冷连轧机轧制力预报模型[J]. 中南大学学报: 自然科学版, 2006, 37(6): 1155-1160.
ZHOU Fu-qiang, CAO Jian-guo, ZHANG Jie, et al. Prediction model of rolling force for tandem cold rolling mill based on neural networks and mathematical models[J]. Journal of Central South University: Natural Science, 2006, 37(6): 1155-1160.

[10] 刘美俊. 基于改进学习算法的模糊神经网络控制系统[J]. 中国电机工程学报, 2007, 27(19): 87-92.
LIU Mei-jun. A fuzzy neural network control system based on improved learning algorithms[J]. Proceedings of the CSEE, 2007, 27(19): 87-92.

[11] 敖 磊, 刘旭东, 吴耀武, 等. 基于改进DFNN的短期电价预测新方法[J]. 继电器, 2006, 34(6): 34-38.
AO Lei, LIU Xu-dong, WU Yao-wu, et al. A new approach to short-term price forecasting based on improved DFNN[J]. Relay, 2006, 34(6): 34-38.

[12] LI Cai, YANG Jie-lin, WANG De-wei, et al. Dynamic route guidance algorithm based on artificial immune system[J]. Journal of Control Theory and Applications, 2007, 5(4): 385-390.

[13] Tarakanov A, Dasgupta D. A formal model of an artificial immune system[J]. Biosystems, 2000, 55(13): 151-158.

[14] LI Ying, Flynn P C. Deregulated power prices: Comparison of volatility[J]. Energy Journal, 2004, 32(14): 1591-1601.

收稿日期：2007-09-10；修回日期：2007-11-21

基金项目：国家自然科学基金资助项目(70572090)；美国能源基金会项目(G-0601-08211)

通信作者：杨尚东(1981-)，男，湖南宁远人，博士，从事电力技术经济、需求管理、智能工程等研究；电话：13910516658；E-mail: yangshangdongbj@126.com