高强度钢板在双向等曲率模中的成形回弹研究
廖娟,周驰,阮锋
(华南理工大学 机械与汽车工程学院,广东 广州,510640)
摘要:针对高强板在双向等曲率模具中的冲压回弹问题进行理论预测及实验研究。在基于塑性膜理论的能量法回弹预测模型中增加考虑弯曲效应对回弹的影响,并采用Khan-Huan本构模型描述高强板的材料应力应变曲线。该解析算法能以较少的计算量获得较为准确的回弹后零件形状。研究结果表明:综合考虑膜效应及弯曲效应后预测的结果比仅考虑膜效应预测模型的预测结果更接近实验值,由该模型预测的2种高强板回弹形状与实际形状的法向平均偏差均小于0.15 mm。
关键词:高强钢;回弹;双曲率;能量法;K-H本构模型
中图分类号:TG386 文献标志码:A 文章编号:1672-7207(2011)06-1629-07
Study on springback of high strength steels deformed
in equal doubly-curved die
LIAO Juan, ZHOU Chi, RUAN Feng
(School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, China)
Abstract: The theoretical prediction and experimental study of springback of high strength steel parts deformed in equal doubly-curved die set were investigated. By incorporating Khan-Huan constitutive model into an energy method based on membrane theory of shells, and taking the bending effect into account, the profiles of the parts after springback was predicted with a relatively minor effort of calculation in the design stage. The experiment results show that the profiles predicted by new model agree better with the experimental results than that predicted by the previous model based on membrane theory. The average normal difference between the predicted profiles and the experimental profiles are less than 0.15 mm.
Key words: high strenth steel; springback; doubly curved; energy approach; K-H constitutive model
随着节能与环保逐渐成为汽车行业的主要需求,汽车轻量化概念应运而生[1]。为了在减少汽车质量的同时,不降低汽车的安全性能,高强板在汽车工业中的应用越来越普遍[2],但是,由于高强板具有较高的屈强比,其回弹问题相对于普通钢板更为严重,因此,也限制了高强板的进一步推广应用[3-7]。冲压回弹是由于卸载后冲压件内部的弹性应变能释放而产生的一个弹性回复过程。对于一个复杂的冲压件,如果将其离散成多个四边形曲面片,回弹问题就转换为各个曲面片单独的弹性应变能释放以及它们之间的互相影响问题。当曲面片足够小时,每个曲面片可以近似地认为是一个双曲率的曲面片。因此,研究双曲率形状冲压件的一些成形特性及规律可以为复杂冲压件回弹的预测及控制奠定一定的基础。对于板料的回弹问题,国内外已经进行了大量的研究工作,但是,大部分的研究主要是针对二维弯曲回弹问题。对于三维板料冲压回弹问题,由于成形的曲面大多数是不可展面,板料在成形过程中不可避免会同时受到膜力和弯矩的作用,两者共同决定板内应力分布和变形模式[8],因此,在成形及回弹的计算过程中需要综合考虑膜力和弯矩的作用。双曲率面是比较典型的不可展面,其变形过程中同样受到膜力和弯矩的共同作用,其力学模型比单纯的二维弯曲变形要复杂许多,回弹的预测及控制也较困难。这方面的研究受到了国内外一些研究者的关注。如:Yu等[9]研究了铜、铝、软钢在双向曲模中的冲压变形过程,得出了不同阶段的变形模型; Parsa等[10]通过物理实验得出了板料厚度及模具曲率对双曲率零件回弹的影响。但是,目前这些研究工作大多是针对普通钢板的,对于高强板在双曲模中的成形特性及回弹规律的研究还比较少。在回弹预测方面,由于有限元方法能处理复杂的几何形状及边界条件,因而在回弹问题的处理上具有不可替代的优势;但 是,有限元方法处理回弹问题时包括成形和预测两部分,成形部分的计算精度对回弹计算的精度产生重要影响,而影响成形精度的因素又非常多,计算所需时间较长,系统开销大[11]。Xue等[12]提出的基于塑性膜理论的能量法预测模型简单易行,具有计算速度快的优点,但其仅能够对膜力占绝对优势的双曲率形状的零件进行快速地回弹预测,并不具有普遍性。本文作者在文献[12]的基础上进一步改进算法,综合考虑弯矩和膜力对回弹的影响,并采用Khan-Huang本构模型[13]来表征高强度钢板的应力应变曲线,建立了方形高强板在双向等曲率模具中的冲压回弹预测模型。最后,进行高强度板在双向等曲率模具中成形的实验研究,探讨其回弹规律,并验证了该预测模型的有效性。
1 能量法预测回弹的理论计算模型
下面的理论分析模型主要针对方形毛坯在双向等曲模冲压下的变形及回弹过程,如图1所示。分析之前,先引入一些基本假设。
1.1 基本假设
(1) 材料是不可压缩的,即变形过程中体积不变。
(2) 忽略横向剪应力。
(3) 材料是非线性硬化的,应力-应变关系采用Khan-Huang本构模型描述。
1.2 能量法求解应变
图1所示为1/4方形毛坯及其成形后的形状(中心层),方板的边长为2a,毛坯以边长为半径分为圆内OAC和圆外ABC 2个部分。在OAC以内,假设沿经线方向将a均分成n段,每段的径向应变设为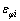 , i=1,2,…,n。当n足够大时,可认为每段内
, i=1,2,…,n。当n足够大时,可认为每段内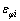 为常量。
为常量。
设成形后球的曲率半径为R。由成形前后的几何与应变关系可以推导出如下第i段周向应变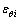 与径向应变的关系[7]。
与径向应变的关系[7]。
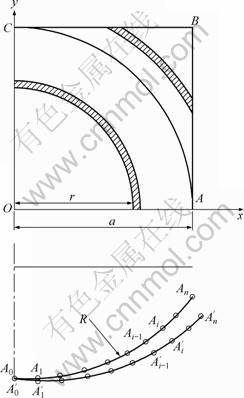
图1 方形板及其离散示意图
Fig.1 Schematic illustration of square plate and its discretization
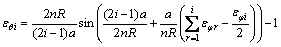 (1)
(1)
由体积不变的假设可知:
 (2)
(2)
其中:εφ,εθ和εz分别为径向、周向及法向的应变。而由塑性形变理论可知:


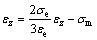 (3)
(3)
式中:σm为平均应力。
设σφ,σθ和σz分别为径向、周向及法向的应力,根据塑性成形原理可知,等效塑性应力σe、等效塑性应变εe分别为:
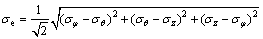 (4)
(4)
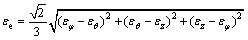 (5)
(5)
平均应力σm为:
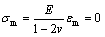 (6)
(6)
式中:E为材料的弹性模量;v为泊松比;εm为平均应变。
由式(2)和(4)可以推出:
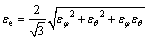 (7)
(7)
由假设(3)及文献[13]得等效应力σe与等效应变εe的表达式:
 (8)
(8)
其中:k1,k2,m1和m2为材料参数。
因此,单位体积内的应变能u为:
 (9)
(9)
由于本文的研究对象为方形板,因此,除了圆形毛坯内部的应变能外,还应加上外围四边角部的应变能,如图1所示,将ABC部分沿径向按相同的宽度继续等分成n′段,假设这部分的周向应变沿半径方向呈线性变化递减,到B点时应变为0。则ABC部分第i段径向应变εφi与周向应变εθi分别为[12]:
εφi,i=n+1,…,n+n′
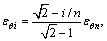 n<i≤n+ n′ (10)
n<i≤n+ n′ (10)
设OAC部分的总应变能为U1,ABC部分的总应变能为U2,ui为第i段的单位体积应变能,h为板料的初始厚度,则在2个区域分别取式(8)体积分可得:

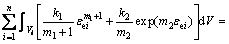
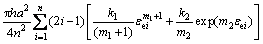 (11)
(11)

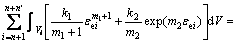

 (12)
(12)
因此,仅考虑膜应变时方形板总应变能为:
U=4(U1+U2) (13)
进一步考虑弯曲的影响,则板沿厚度方向划分的各层纤维中有部分将被拉伸,部分将被压缩,各层应变值不能单由中心层应变来代替。
考虑弯曲效应时需增加2个假设:
(1) 弯曲变形前后板料厚度变化可以忽略;
(2) 弯曲变形前后截面满足平截面假设。
如图2所示,将厚度为h的板划分成2n1+1层,每层的厚度为h1=h/(2n1+1),则从中心层算起的第q层第i段的径向应变εφiq和周向应变εθiq分别为[14]:
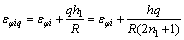
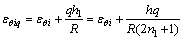 (14)
(14)
其中: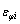 和
和 为第i段中心层的膜应变,其表达式见式(1)。由式(13)计算时,q的符号如此规定:q为压缩层时为负,为拉伸层则为正。
为第i段中心层的膜应变,其表达式见式(1)。由式(13)计算时,q的符号如此规定:q为压缩层时为负,为拉伸层则为正。

图2 板弯曲示意图
Fig.2 Schematic illustration of a bent plate
将式(13)代入式(6)可得第q层的等效应变εeiq为:
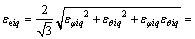
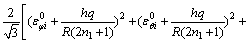
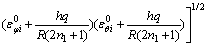 (15)
(15)
将式(14)的εeiq代替式(10)和(11)中的εei,可得第q层的应变能U1q和U2q的表达式,再对各层的应变能求和,则可得考虑膜效应及弯曲效应的整个壳的总应变能为:
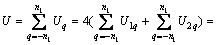

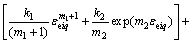

 (16)
(16)
根据最小能量原理,在一切满足条件的应变场中,只有使系统总能量为最小的应变,才是真实的应变,因此,有:
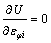 ,i=1,2,…,n+n′ (17)
,i=1,2,…,n+n′ (17)
由此可以得到n+n′个非线性方程组,从而可以解出沿经线方向的各段应变,再由式(1)和(9)可以分别算出OAC及ABC部分圆周方向中心层的应变εθi。
1.3 回弹预测
1.3.1 膜效应引起的回弹
当卸除外加冲压力后,工件由于弹性应变的释放而产生回弹。根据广义虎克定律,可知卸载引起的中心层第i小段径向弹性应变ε′φi及周向弹性应变ε′θi分别为:
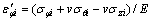
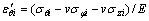 (18)
(18)
结合式(3)和(5),式(17)可简化为:
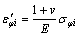
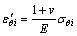 (19)
(19)
工件卸载后,由于弹性应变的释放从而产生回弹,零件几何形状的变化如图1所示。由应变与几何关系可以推导出中心层回弹后第A′i点的坐标(xi,yi)[12]:
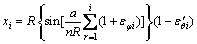
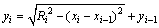 (20)
(20)
其中:
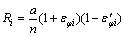 (21)
(21)
由式(20)即可求得膜效应引起的工件的回弹后各点坐标xi和yi。
1.3.2 弯曲效应引起的回弹
根据弯矩定义可知,施加在板横截面上的径向弯矩Mφi、周向弯矩Mθi(单位宽度)分别为:
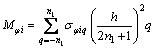
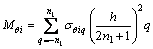 (22)
(22)
由式(3)和(7)得σφiq及σθiq,再代入式(21)可得:
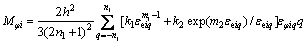
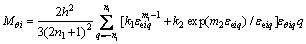 (23)
(23)
根据板壳弯曲理论,弯矩卸载后所引起的径向曲率变化量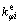 和周向曲率变化量
和周向曲率变化量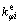 为:
为:
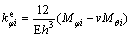
 (24)
(24)
回弹后中心层的径向曲率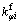 应该满足下式:
应该满足下式:
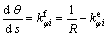 (25)
(25)
已知回弹后曲线的曲率求回弹后的曲线形状,这里采用文献[15]所提出的分段近似求解,当段距足够小时,可以将任意小段的曲率看成是沿弧长线性变化的,即
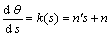 (26)
(26)
其中:s为弧长;θ为曲线的切线方向角;k为曲率;m和n为参数。然后,根据曲线的微分几何理论推导可求得下式(推导过程见文献[10]):
 (27)
(27)
根据每段的曲率弧长可以分段求出参数mi和ni,而参数ci则由每段的边界条件决定。
第i段的弧长计算公式为:
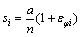 (28)
(28)
采用数值方法求解式(26),可以求得第i点由弯矩卸载引起的回弹后零件各坐标x′i和y′i。
将膜效应及弯曲效应引起的回弹进行叠加,可预测出工件最终的回弹后零件各点最终坐标位置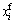 ,
,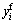 分别为[9]:
分别为[9]:

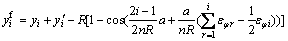 (29)
(29)
得到各点坐标后,采用样条曲线进行拟合,即可得回弹后零件最终形状。
2 实例研究
为了验证上述理论,下面对1个实例进行预测。零件尺寸如图3所示,其中R1=R2=180 mm,2a=150 mm。
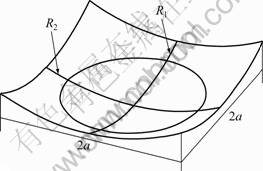
图3 实验模具尺寸示意图
Fig.3 Dimensions of the experimental die
为了便于对比,实验采用5种厚度均为1 mm的材料进行冲压,其中包括2种高强度板Docal 1000DP和Docal 1200M。5种材料的应力-应变曲线如图4 所示。
2.1 计算与实验结果的比较
根据1.2节的算法对2种高强度板在上述双曲模中成形后的应力应变进行求解,计算中2种高强板的K-H本构模型中的参数取值,如表1所示。计算后可得出试件成形末端的应力和应变。图5所示是当n取30时计算出的高强板Docal 1000DP各小段的径向、周向及等效应力。
求得各应力后根据1.3节中的算法进行回弹预测。图6所示为Docal 1000DP与Docal 1200M 2种试件的预测回弹形状。其中:预测形状1表示的是仅考虑膜效应预测所得回弹形状,预测形状2为综合考虑膜效应及弯曲效应所得回弹形状。表2所示为2种预测形状与实验所得形状的最大法向偏差及平均法向偏差。由表2可知:预测模型2预测的高强板Docal 1000DP与Docal 1200M的平均法向偏差比预测模型1分别减少了82%及71%。同时,由表2及图6可以看出:膜效应对回弹的影响不可忽略,但是,综合考虑膜效应及弯曲效应后预测的形状更接近实验所得回弹形状。改进后预测模型的最大法向偏差均小于0.35 mm,平均法向偏差均小于0.15 mm。

图4 5种材料的真应力-真应变曲线
Fig.4 Stress-strain curves of five materials
表1 2种高强板的K-H本构模型拟合参数
Table 1 Parameters in K-H constitutive model of two AHSS

图5 Docal 1000DP 板成形后各段的径向、周向及等效应力
Fig.5 Stress in meridional, circumferential direction and effect stress of deformed plates made of Docal 1000DP
表2 理论预测形状与实验所得形状偏差对比
Table 2 Difference comparison between prediction profiles and experiments
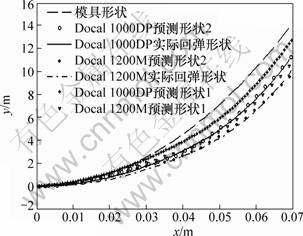
图6 Docal 1000DP与Docal 1200M 的理论预测回弹形状与实验结果对比
Fig.6 Comparison of profiles of sheets made of Docal 1000DP and Docal 1200M obtained by theoretical prediction and stamping
2.2 结果讨论
2.2.1 最终曲率的分布
图7所示为高强板Docal 1000DP在冲压力分别为320 kN和640 kN下的最终曲率k1和k2为弧长的关系对比。由图7可见:k1和k2均表现为中间部分曲率波动较均匀,靠外缘部分曲率波动较大,临界点位于弧长比例s约0.25及0.75处,这一现象在其他几种材料上也有发现,不过高强板的曲率突变更为明显。与试件比照可知,曲率的高峰值对应板边缘轻微起皱的 部分。
由图5可知:该曲率突变点刚好与周向应力为零(约第15段处)的临界点对应,当0.25<s<0.75时,板处于双向受拉的状态;而当s<0.25或s>0.75时,板处于径向受拉,周向受压的状态,因而更容易起皱。
2.2.2 回弹影响因素分析
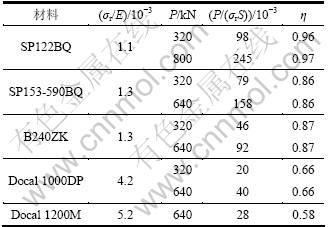
根据Yu等[9]的研究发现:当无量纲冲压力P/(σrS)满足P/(σrS)>h/(2R),平均回弹比η几乎趋于常数。其中,P为冲压力;σr为屈服强度;S为零件横截面积;h为板料厚度;R为双向等曲率零件的曲率半径。对于本例这个临界值为2.8×10-3,实验对不同材料设置了不同的无量纲冲压力,所设置的各冲压力均远大于该临界值。
表3所示为本次冲压实验的方案及所得结果。由表3可以看出:在超过临界值之后,冲压力的改变对平均回弹比的影响非常小。材料参数对平均回弹比的影响比较大。从整体看,随着材料屈弹比σr/E的增大,η减小,回弹增大。2种高强板的回弹明显比前3种材料要大很多,Docal 1200M的回弹最大,回弹比达到了0.58。
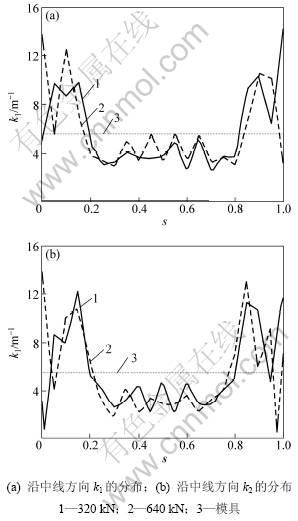
图7 Docal 1000 DP板在冲压力分别为320 kN和640 kN作用下k1和k2的分布
Fig.7 Distribution of final curvature of Docal 1000DP plates after being pressed by pressures of 320 kN and 640 kN
表3 不同材料在不同冲压力下试件的回弹比
Table 3 Ratios of springback for different materials under different stamping forces
3 结论
(1) 在双曲率零件的成形回弹过程中,膜效应与弯曲效应对回弹的影响需要同时考虑,综合考虑2种效应的预测模型所得结果更加接近实验结果。2种高强板预测形状与实际的平均法向偏差均小于 0.15 mm。
(2) 当冲压力满足P/(σrS)>h/(2R)的情况下,进一步增大冲压力对试件回弹的影响不明显;而材料的屈弹比对试件的回弹影响很大;随着屈弹比的增加,回弹增大,特别是高强板,其回弹量甚至比一些普通钢板的回弹量高约40%。
参考文献:
[1] ZHANG Yan, LAI Xin-min. Lightweight design of automobile component using high strength steel based on dent resistance[J]. Materials & Design, 2006, 27(1): 64-68.
[2] CHEN Peng, Muammer K, Wenner-Michael L. Experimental investigation of springback variation in forming of high strength steels[J]. Journal of Manufacturing Science and Engineering, 2008, 130(4): 61-69.
[3] Mori K, Akita K, Abe Y. Springback behaviour in bending of ultra-high-strength steel sheets using CNC servo press[J]. International Journal of Machine Tools and Manufacture, February, 2007, 47(2): 321-325.
[4] Merklein M, Kaupper M. Manufacturing of innovative car seat components by forming of advanced high strength steels—Fundamental research and application[J]. Key Engineering Materials, 2009, 410/411: 3-11.
[5] CHEN Ke, LIN Jian-ping, L? Mao-kang. Advanced high strength steel sheet forming and springback simulation[J]. Advanced Materials Research, 2010, 97/101: 200-203.
[6] GUO Chao-qun, CHEN Jun, Jie-shi. Numerical simulation and experimental validation of distortional springback of advanced high-strength steel sheet metal forming[J]. Journal of Shanghai Jiaotong University, 2010, 44(4): 468-482.
[7] Zhang X K, Zheng G J. Compensation factor method for modeling springback of auto parts constructed with high-strength steel[J]. International Journal of Automotive Technology, 2010, 119(5): 721-727.
[8] Ventsel E, Krauthammer T, Krauthammer T. Thin plates and shells: theory, analysis, and applications[M]. New York: The Chemical Rubber Company Press, 2001: 3-4.
[9] Yu T X, Johnson W. Stamping rectangular plates into doubly-curved dies[J]. Proc Instn Mech Engrs, 1984, 198(8): 709-125.
[10] Parsa M H, Kazemi M. Study the effect of curvature on springback of double curved steel sheet using new method[C]// Proceedings of the 9th International Conference on Numerical Methods in Industrial Forming Processes. Porto: American Institute of Physics, 2007: 901-906.
[11] 周驰, 刘强, 阮锋, 等. 一种基于能量法的冲压回弹预测补偿算法[J]. 塑性工程学报, 2008, 15(2): 131-135.
ZHOU Chi, LIU Qiang, RUAN Feng. An energy approach for stamping springback prediction and compensation[J]. Journal of Plasticity Engineering, 2008, 15(2): 131-135.
[12] Xue P, Yu T X. Theoretical prediction of the springback of metal sheets after a double-curvature forming operation[J]. Journal of Material Processing Technology, 1999, 89/90: 65-71.
[13] LIANG Ri-qiang, Khan A S. A critical review of experimental results and constitutive models for BCC and FCC metals over a wide range of strain rates and temperatures[J]. International Journal of Plasticity, 1999, 15(9): 963-980.
[14] Xue P, Yu T X. An energy approach for predicting springback of metal sheets after double-curvature forming (Part I): Axisymmetric stamping[J]. International Journal of Mechanical Sciences, 2001, 43(8): 1893-1914.
[15] LIAO Juan, ZHOU Chi. A new springback compensation method for sheet metal bending based on curvature correction[J]. Advanced Materials Research, 2010, 97/101: 130-134.
(编辑 陈爱华)
收稿日期:2010-05-08;修回日期:2010-07-08
基金项目:国家自然科学基金资助项目(50805050);广东高校优秀青年创新人才培育项目(2009N9090180)
通信作者:阮锋(1946-),男,广东潮州人,教授,博士生导师,从事塑性加工与模具计算机技术研究;电话:020-22236388;E-mail:mefruan@scut.edu.cn