模具入口几何形状对弯曲模挤压四叶草形状坏料的影响:上限分析和实验验证
来源期刊:中国有色金属学报(英文版)2013年第4期
论文作者:Tahir ALTINBALIK Onder AYER
文章页码:1098 - 1107
关键词:挤压;四叶草形状;上限分析法;最佳模具形状
Key words:extrusion; clover section; upper bound; optimal die profile
摘 要:对模具入口、过渡区几何形状对挤压载荷和材料流动的影响进行了理论和实验研究。选取的模具形状有4种,分别为截面为圆形、四叶草形的直锥模,截面为圆形、四叶草形的余弦弯模。工业纯铅因其室温热变形能力强而被选作实验材料。根据上限分析法,提出一个新的运动许可速度场来分析四叶草形模具挤压圆坏得到的压件形状。理论分析得到的不同模具入口、过渡区几何形状挤压载荷与实验结果一致。以挤压件的轴向偏差来衡量产品质量尺寸方面的好坏。
Abstract: The effect of die inlet and transition geometry on the extrusion loads and material flow for extrusion of clover sections were investigated and presented both theoretically and experimentally. For this purpose, four different die geometries including straight tapered and cosine transition profile and each of them having round and clover inlet geometries were chosen. In the experimental study, commercially pure lead was used because of its hot forming characteristic at room temperature. A newly kinematical admissible velocity field to analyze different profiles of extrusion dies of clover section from round bars was proposed by upper bound analysis. It is clear that the extrusion loads obtained from the theoretical analysis for various die inlet-die transition geometry combinations are in good agreement with the experimental results. Axis deviations of the parts which define the dimensional quality of the products were also investigated.
Trans. Nonferrous Met. Soc. China 23(2013) 1098-1107
Tahir ALTINBALIK, Onder AYER
Department of Mechanical Engineering, Faculty of Engineering and Architecture, Trakya University, 22180 Edirne, Turkey
Received 20 April 2012; accepted 3 March 2013
Abstract: The effect of die inlet and transition geometry on the extrusion loads and material flow for extrusion of clover sections were investigated and presented both theoretically and experimentally. For this purpose, four different die geometries including straight tapered and cosine transition profile and each of them having round and clover inlet geometries were chosen. In the experimental study, commercially pure lead was used because of its hot forming characteristic at room temperature. A newly kinematical admissible velocity field to analyze different profiles of extrusion dies of clover section from round bars was proposed by upper bound analysis. It is clear that the extrusion loads obtained from the theoretical analysis for various die inlet-die transition geometry combinations are in good agreement with the experimental results. Axis deviations of the parts which define the dimensional quality of the products were also investigated.
Key words: extrusion; clover section; upper bound; optimal die profile
1 Introduction
Extrusion is a plastic deformation process in which a workpiece is reduced in cross-section by forcing it through the die opening of a small cross-sectional area than that of the original billet. The direct extrusion of rods and solid shapes is the simplest production method in use for high production rate and accuracy. Extrusion technology is developing rapidly to meet the cost of production in the recently competitive market. The most important factor that affects the quality of extrudate is the material flow. The optimum die surface design will produce a smooth material flow during the extrusion process and, therefore, a high quality extrusion. The design of the tooling is a decisive factor in rod and solid shape extrusion [1]. The metal flow in extrusion is influenced by many factors such as type and speed of extrusion, billet material properties at extrusion temperature, frictional conditions, type-layout and design of die and extrusion ratio.
In the past, conical dies were preferred to curved dies because of easy manufacture. Nowadays, the manufacture of curved dies has become an easy operation process using CNC machines. Thus, researchers have easily developed techniques to design curved die profiles for the forward extrusion. Especially during the last two decades, researchers have paid attention to curved dies such as linearly converging die profile and cosine die profile. Curved dies cover an area of application from simple axisymmetric products to complicated sections such as gears and splines [2].
A number of analytical studies have been performed during the past few decades to compute the forming load for the extrusion of metal through a variety of die shapes such as curved or conical. In the mentioned studies, researchers analyzed extrusion processes of different sections by slab method, finite element method and upper bound approach [3,4]. Formerly, CHEN and LING [5] developed a velocity field for axisymmetric extrusions through cosine, elliptic and hyperbolic dies. JUNEJA and PRAKASH [6] made upper bound solutions for the extrusion of polygonal sections from polygonal billets by means of the spherical velocity field. To eliminate the restriction of cross-sectional shape of sections, YANG and LEE [7] performed the conformal mapping approach to obtain a kinematically admissible velocity field for extrusion through concave and convex shaped dies. GUNASEKERA and HOSHINO [8] obtained an upper-bound solution for the extrusion of polygonal sections from round billet through converging dies formed by a smooth curved streamlines. Surface of dead metal zone was assumed as a die profile and given by radius function. The authors also asserted that the present analysis was applicable to other curved dies such as parabolic, convex or concave shapes by changing the profile function of f(z). A kinematically admissible velocity field for a generalized three-dimensional extrusion of arbitrarily shaped sections was derived, in which all the velocity components were expressed in general function forms by HAN et al [9]. Die surface representation was proposed, by which there was a smooth transition of die contour from the entrance to exit. Extrusion of clover section from round billets was chosen as a computational example. YANG et al [10] performed a new die design method using surface blending and Fourier series for three-dimensional extrusion of arbitrarily shaped sections in the light of their previous work done by HAN et al [9]. LEE et al [11] used a general surface model to express the die geometry R(θ, z). The die surface was optimized by using the upper bound analysis to minimize the extrusion pressure required. SHEU and LEE [12] adopted the kinematically admissible velocity field proposed by HAN et al [9] and die surface was expressed by an analytical function R(θ, z). Then, they performed extrusion tests for straight-sided gear splines from round bars to obtain the extrusion load and compared with those obtained from upper bound analysis. A theoretical analysis was performed by MAITY et al [13] for the extrusion of square sections from using curved dies by means of the upper bound analysis. Nine different die geometries used by the authors and the cosine, elliptic, circular, parabolic and hyperbolic dies were given in die-profile functions. An incremental slab method to calculate the extrusion pressure for arbitrarily curved dies was implemented by WIFI et al [14]. They suggested that the slab method could be used to obtain the extrusion pressure for curved dies as well as for conical dies, and offered that the incremental slab technique should be used to extrusion ratios below 34.6. SAHOO et al [15] applied the reformulated spatial elementary rigid region (SERR) technique to extrude from round billets to polygon sections through linearly converging die. SHEU [16] used a CAD/CAM/CAE integration system for the design and manufacturing of die surface for cold extrusion and die surface was optimized to give a lower power consumption by the upper bound method.
Recently, ONUH et al [17] carried out a number of experiments by choosing a gear-like section to obtain the effect of the die geometry and extrusion speed on the cold extrusion of aluminum and lead alloys. The optimum die profile in cold-rod extrusion of aluminum with work-hardening was obtained by NOORANI et al [18]. They also performed serious experiments for optimum curved die and optimum conical die. AJIBOYE and ADEYEMI [19] made an experimental and theoretical study to obtain the effect of die land length on the quality of extruded product. A combined upper bound and slab method was developed by JOOYBARI et al [20] to obtain the deformation load in forward rod extrusion. The authors performed study for the two dies, optimum conical die and optimum curved die. GORDON et al [21-23] performed a series of studies to develop the flexible velocity fields that could be used in an upper bound model for flow of a perfectly plastic material during extrusion through dies of any shape. For this purpose, six flexible velocity fields for axisymmetric extrusion were derived in the first part of the studies. In the second paper, the results for extrusion through a spherical die shape using the six velocity fields which were derived in the first paper were compared to determine which velocity field is the most suitable. The results demonstrated that the sine-based velocity field is better than the angular-based or area-based velocity fields. In the last part of the studies, the results of the upper bound model using the sine-based velocity field were compared with the model on an arbitrarily curved streamlined die which had previously been done and published by YANG et al [10]. ALTINBALIK and AYER [24,25] performed a series studies for the extrusion of clover sections which are used for trochoidal gears of external gear pumps. The clover section is also a preform of the spur gears. In these studies, new kinematically admissible velocity fields for three dimensional extrusion were suggested for both obtaining the optimum die length of shaped inlet dies and determining the extrusion load. Four kinds of die profiles including cosine, conic, elliptic and hyperbolic dies were investigated both theoretically and experimentally by HUANG et al [26]. The analytical studies were performed by the upper bound method.
In the presented study, the extrusion of clover section, as an example, from round billets was chosen, which was often used for cams and trochoidal gears of external gear pumps. Such a section, on the other hand, is also a preform of the spur gear. Four different extrusion die geometries, including straight tapered transition and cosine transition die profile with round and clover inlet geometries, were chosen for the experiments to obtain the clover shaped product. Then, a new kinematical velocity field was proposed for the four different situations and determined the best die profile by means of the optimal extrusion load.
2 Theoretical analysis
The metal flow in the extrusion process is an important factor controlling the mechanical property of the extruded products. It is difficult to predict the metal flow in three-dimensional extrusion of complicated sections due to the difficulty in representing the geometry of the die surface and in expressing the corresponding velocity field. Upper bound analysis has been chosen for mathematically modelling of the process. Upper bound analysis is the most practical method and involves the construction of a kinematically admissible velocity field for a given deformation process. An important step in upper bound analysis is to propose a velocity field, which minimises the power dissipated during the deformation. To simplify the calculations, the following assumptions are made: 1) the punch and container are considered rigid body and the material is assumed to be isotropic, incompressible, rigid-plastic and obeys von Mises flow rule; 2) the friction factor between die-material contact surface is constant. It is well known that the kinematically admissible velocity field of the workpiece should satisfy the volume constancy and boundary condition.
The upper bound formulation for total rate of energy dissipation during the deformation is given as follows:
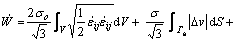
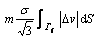 (1)
(1)
The first right hand term of Eq. (1) represents the internal power dissipated over the volume V; the second term represents the shear losses; and the third term represents the frictional losses on the tool-workpiece interface; Гs represents the area of the velocity discontinuity; Гf defines frictional surfaces. s0 is the flow stress of material; eij the derived strain rate tensor, |Dv| is the velocity discontinuity over the shear surfaces; m is the friction factor.
3 Mathematical modelling of dies
Clover extrusion is the complex section, and in the case of a smooth product section which can be expressed by an analytical function, a surface die can be easily designed and manufactured. So, in this study, extrusion of the clover section was chosen from round billets. Then, four different situations were investigated with two different die inlet geometries such as round inlet and clover inlet; and each of them has two pre-defined die transition profiles such as straight tapered and cosine curved as seen clearly in Figs. 1 and 2 with the tool assembly. Cylindrical coordinate system (r, θ, z) was used to define the geometrical expressions of the die profiles. Figure 3 shows the generalized shape and dimensions of the die surfaces used for numerical calculations. Shape functions were defined according to inlet and outlet geometries. These shape functions not only model the material flow but also define the die profile in which the material flows. These shape functions were used to model the metal flow and help to determine the better die profile.
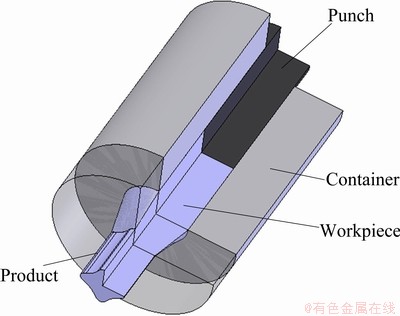
Fig. 1 Schematic illustration of die assembly
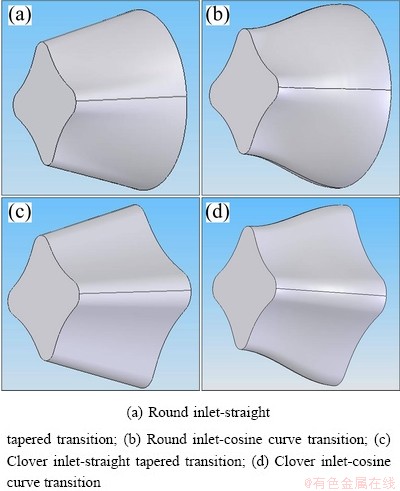
Fig. 2 Profiles of various curved dies
Die profiles of deformation zone in terms of inlet and outlet dimensions can be given for straight tapered and cosine curved, respectively, as follows:
 (2)
(2)
 (3)
(3)
where L is the length of the dies and constant for all types of dies; R0 and Rf help to obtain the radius function given in Eqs. (2)-(3) and can be described as follows:
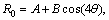
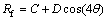 (4)
(4)
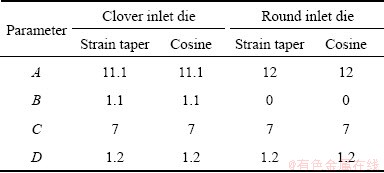
where parameters A, B, C and D are related with the inlet and outlet geometries and dimensions of the dies. Countless inlet and outlet die geometry can be defined by changing these parameters A, B, C and D. For example, B should be chosen as 0 to convert the inlet profile to round shape and for 0<B<A it can obtain smooth clover section inlet profile. The values of these parameters are given in Table1 for die sets used in the presented study.
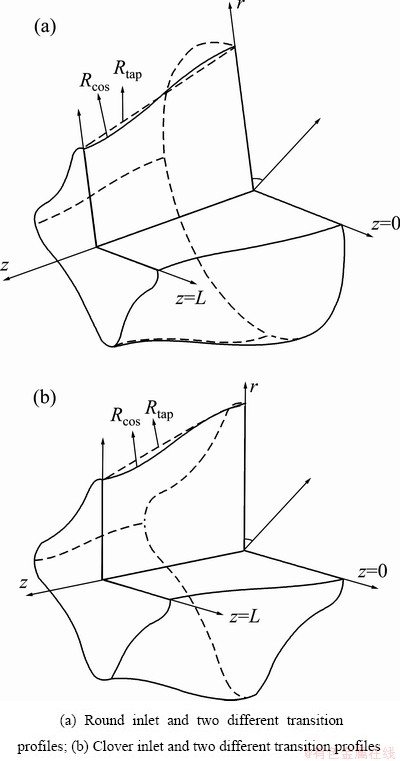
Fig. 3 Proposed kinematically admissible velocity fields for clover section
Table 1 Specific die parameters for mathematical expression of die types
4 Generalized velocity fields and UB solutions
In Table 2 it can be seen that the proposed kinematically admissible velocity fields are used for two different die profiles. As it is known these velocity fields must satisfy the boundary conditions.
Table 2 Proposed kinematically velocity fields
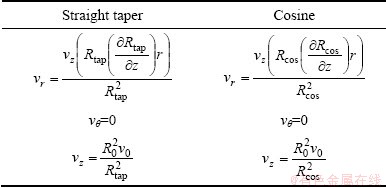
For cylindrical coordinates, strain rates can be derived from velocity fields given in Table 2 by the equations as follows:
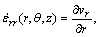
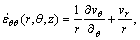
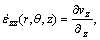

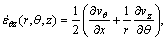
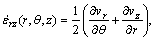
 (5)
(5)
For cosine curved profile die, strain rates are calculated according to proposed velocity fields as follows:
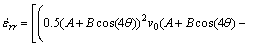
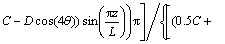
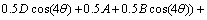
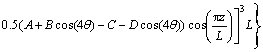 (6)
(6)
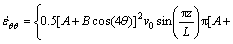
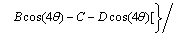
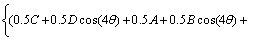
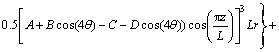
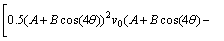
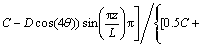
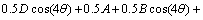
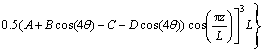 (7)
(7)
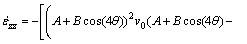
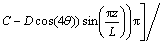


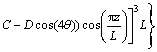 (8)
(8)
and for straight tapered die, strain rates are calculated according to proposed velocity fields as follows:
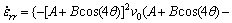
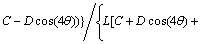
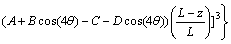 (9)
(9)


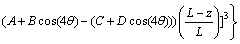 (10)
(10)

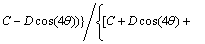
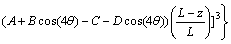 (11)
(11)
Rest of strain rates such as εrz can be derived from Eq. (5).
The rate of internal deformation energy dissipation can be calculated as follows:
 (12)
(12)
The rate of shear loss over shear surfaces is determined from the velocity fields given in Table 1 as follows:
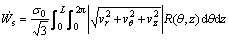 (13)
(13)
Frictional power loss in the extrusion die wall/material interface is given as follows:

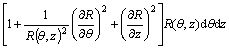 (14)
(14)
Total power consumption required to extrude the billet to clover section over the profiled dies is obtained by summing all the power components given in Eqs. (12)-(14):
 (15)
(15)
Total power consumption can also be written in another form as follows:
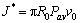 (16)
(16)
where v0 is the ram velocity. The required extrusion load is given as follows:
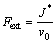 (17)
(17)
5 Experimental study
A series of experiments for clover extrusion were carried out to obtain the optimum die surface design and compare the measured experimental loads values with those calculated from UB. Experiment material has been chosen as commercially pure lead because of its hot forming characteristic at the room temperature. The cylindrical billets were extruded from a cylinder of 40 mm to 24.0 mm and machined to the 50 mm length. Extrusion container with internal diameter of 24.2 mm having 55 mm outer diameter and punch were machined. The die geometries chosen in the present investigation were cosine curved and straight tapered which have round and clover inlet and clover outlet explained before. The extrusion ratio is given by R=(Ainlet/Aoutlet) and it is obtained R=3.2 for round inlet specimens and R=2.1 for clover inlet specimens. The tool assembly, dies and experimental set-up are shown in Fig. 4. Die length was determined as 15 mm from UB solution of previous work [25]. As a result of the geometries, die land length/billet diameter ratio was calculated to be 0.625, which means greater value of 0.6 as recommended by AJIBOYE and ADEYEMI [19]. Dies were machined at CNC due to geometrical complexity. Extrusion die, containers and the punches were made from 1.2344 DIN hot worked tool steel and hardened to HRC54. After compression test of lead specimens, flow stress was constant and determined as s0=24 MPa. Experiments were carried out on a 1500 kN ton hydraulic press with constant ram speed of 5 mm/s. The lead specimens were cleaned with acetone before deformation in order to ensure the similar friction conditions. The hydraulic press was equipped with a pressure-current transducer in order to measure and record the experimental load. On the other hand, the required stroke of the press was adjusted by a vernier ruler which has an inductive switch at the end. Thus, the upper plate of the press reached the adjusted position of 37 mm punch stroke, and then the experiment was stopped by means of the software. Graphics of the load- stoke were drawn by software.

Fig. 4 Photographic views of dies (a) and experimental set-up for extrusion of clover sections (b)

Fig. 5 Comparison between theoretical and experimental load values of round inlet-straight tapered transition die
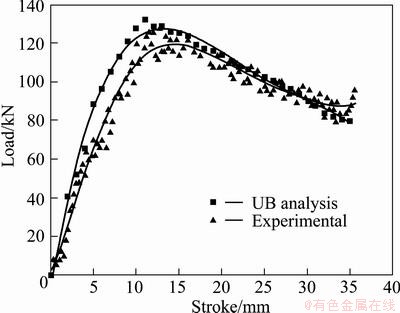
Fig. 6 Comparison between theoretical and experimental load values of round inlet-cosine curve transition die
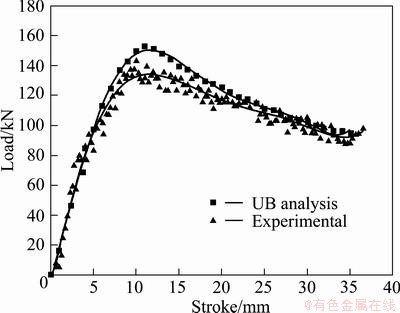
Fig. 7 Comparison between theoretical and experimental load values of clover inlet-straight tapered transition die

Fig. 8 Comparison between theoretical and experimental load values of clover inlet-cosine curve transition die
6 Results and discussion
In this work, a new kinematically admissible velocity field was derived for simulating the profile of the extrusion die. The round to polygonal section is the most typical industrial extrusion, but in the present work two different inlet geometries and each of them having two different die surface profiles were analyzed by means of UB analysis. The outlet geometry was chosen as a clover section because of its complex geometry.
Figures 5-8 show a comparison of forming load versus the punch stroke between the experimental and theoretical results for different die profiles. As can be seen in these figures, the forming load increases as the punch moves downward due to the increase in frictional surfaces. As the process continues, the forming load decreases until the last stage and then increases again sharply because of the upper and lower dead zones facing each other. So, the curves emphasize the three stages of extrusion, compression, steady and unsteady stages. The theoretical predictions are somewhat higher than the experimental ones as expected. In Fig. 5, the theoretically estimated load values and the experimental recorded are shown for straight tapered profiled dies with round inlet geometry to obtain the clover section. The prediction of the maximum extrusion load is very important in order to design all forming parameters such as die design, tool material selection. According to Fig. 5(a), good agreement can be seen between the theoretical results and the experiments. As expected, the theoretical results are found to be higher than the experimental results. The maximum difference is about 5.5% and this discrepancy is a reasonable one. Kinematically admissible velocity fields do not valid at the end of the process, so sharp increase is not seen in the analysis’ diagram. Also, Figs. 6-8 suggest that upper bound solutions are valid for the other die types. The loads against punch stroke obtained as a result of the experiments with a round inlet-cosine transition profiled die are given together with the upper bound solution results in Fig. 6. The maximum load of the upper bound calculated deviates from the value obtained experimentally only 4.7%. A similar observation can be made with the clover inlet-straight tapered transition die as seen in Fig. 7 and clover inlet-cosine curve transition die in Fig. 8, respectively. The difference between the experimentally measured and analytically obtained values at the maximum is 6.3% for clover inlet-straight tapered transition die and 7.9% for clover inlet-cosine curve transition die. From Figs. 5-8 the upper bound solution is reasonable with those measured from experiments; analysis is assumed to be valid.
From Figs. 5-8, it is seen that the extrusion load for clover section inlet dies is a little higher than that for the round section because the entrance of the round billet is more difficult into clover inlet dies. Figure 9 illustrates the comparison of relative punch pressure against the friction factor for four different die geometries in order to evaluate the die profile effects clearly. From the diagram, the total relative punch pressure increases linearly with increasing friction factor due to the frictional portion of the total pressure of the upper bound solution. Furthermore, relative punch pressure is higher for the clover inlet dies compared with the round inlet dies in each friction factor. On one hand, another interesting point is that the difference between straight tapered dies and cosine profiled dies, in terms of relative punch pressure, increases with increasing the friction factor. Straight tapered dies need less deformation energy, especially higher friction factor because the straight tapered dies have less interface area compared with the cosine dies. On the other hand, there is a difference in determined radius function between two transition geometries.
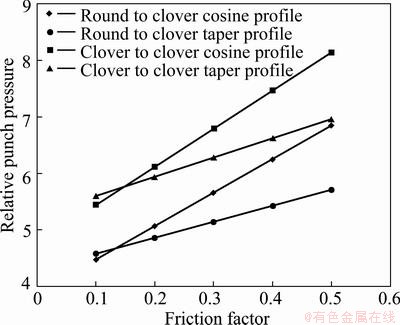
Fig. 9 Relationship between friction factor and relative punch pressures for all type of dies
Round inlet dies were examined in detail because the less extrusion load is obtained from round inlet dies. Figures 10 and 11 illustrate the total extrusion load obtained from the upper bound solutions and each component. The maximum friction load at given stroke is about 33% of total extrusion load for the straight tapered transition die. For the same die, the friction load is about 12% of the total load when the extrusion load is its maximum value. For the cosine profile transition die, the friction load is about 20% of the total load when the extrusion load is at its maximum value. The reason is that interface area of cosine profiled die is bigger as explained before. The load required to overcome the friction in tapered die is 45% lower than that in cosine profile at the maximum load. However, the die surface is shown to have smooth transitions throughout the whole region for the cosine transition die as expected. For this reason, the load required to overcome shear losses in the cosine profiled die is 35% lower than that in the straight tapered die.

Fig. 10 Relationship between stroke and components of extrusion load obtained from UB analysis for round inlet-straight tapered transition die
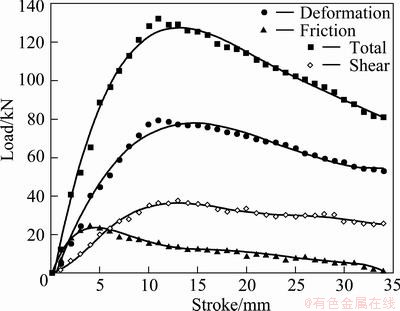
Fig. 11 Relationship between stroke and components of extrusion load obtained from UB analysis for round inlet-cosine curve transition die
In this study, dimensional accuracy and deviation from the axis defining the dimensional quality of product were investigated. It is known that the European specifications require that the average dimension deviations should not exceed 1% on general dimensions and 5% on thickness [24]. The final dimensions of parts obtained from the experiments were measured by using MitutoyoXC20 3D equipment and acceptable dimensional accuracy was observed. The difference between the dimensions of the extruded product and the dimensions of the die varies in 0.02-0.11 mm. Besides, in order to obtain the effect of die transition profile on axial deviation, deviation from the part axis was controlled by Zeiss conturoscope and shown in Fig. 12. Measurements were done at equal distances from the tip of the extruded specimen. Axial deviation in cosine profiled die which is smoother compared with the tapered die is 40% better than that in straight tapered profile.

Fig. 12 Axis deviation results of extruded products for various die types
7 Conclusions
Detailed experimental and theoretical investigations have been performed and firstly, a new kinematically admissible velocity field has been proposed to predict the load requirement for forward extrusion of clover section to determine the die inlet-transition combination effect. This is performed for the four dies combinations: optimal conical die with two different die inlet geometries and optimal cosine die with two different die inlet geometries. Die transition surfaces have been defined by a general radius function R(θ,z) and derived. This method provides that there is no need to find analytical functions or specify product sections segment by segment. On the one hand, the derived velocity field is applicable to three- dimensional extrusion of other complex shape, for which the die surface can be defined by an analytical function and can be used for load calculation as a first approximation for a design engineer. The upper bound solutions presented in this study are in agreement with the experimental results, which meet the demand of calculation of the punch pressure of forward extrusion. Load requirement for round inlet/straight tapered transition profiled die in forward extrusion is about 8% less than that of round inlet/cosine transition profiled die. Forming load obtained from round inlet/straight tapered transition profiled die is about 18% less than that for clover inlet dies. On the other hand, in the theoretical analysis round inlet/straight tapered transition profiled die has given the lower upper-bound pressure than others. The proposed analytical function model takes less computational time than the study done by HAN et al [9]. In an other study done by authors [27], the load obtained from DEFORM 3D solution using same dies is more than 14% than the experimental values. So, upper bound analysis gives more realistic solution for this process. The effect of friction on relative punch pressure has also been discussed. Product quality in terms of dimensional accuracy has been investigated and cosine curved transition dies provides less axial deviation. The results of the influence of the die shape on the flow deformation in this study could be expanded to the design of more complex shaped extruded products.
Acknowledgements
The authors wish to thank Hema Industry for technical support in the controlling of the dimensional accuracy and the deviation from the axis.
References
[1] SHEPPARD T. Extrusion of aluminium alloys [M]. The Netherlands: Kluwer Academic Publishers, 1999: 12.
[2] LEE S K, KO D C, KIM B M. Optimal die profile design for uniform microstructure in hot extrusion [J]. Int J Mach Tools & Manuf, 2000, 40: 1457-1478.
[3] CHANG K T, CHOI J C. Upper-bound solutions to extrusion problems through curved dies [C]//Proc 12th Midwestern Mechanics Conference Paris: University of Notre Dame, 1971: 383-396.
[4] NAGPAL V. General kinematically admissible velocity field for some axisymmetric metal forming problems [J]. Trans ASME; J Eng Industry, 1974, 96: 1197-1201.
[5] CHEN C T, LING F F. Upper bound solutions to axisymmetric extrusion problems [J]. Int J Mech Sci, 1968, 10: 863-879.
[6] JUNEJA B L, PRAKASH R. An analysis for drawing and extrusion of polygonal sections [J]. Int J Mach Tool Des Res, 1975, 15: 1-30.
[7] YANG D Y, LEE C H. Analysis of three-dimensional extrusion of sections through curved dies by conformal transformation [J]. Int J Mech Sci, 1978, 20: 541-552.
[8] GUNASEKERA J S, HOSHINO S. Analysis of extrusion of polygonal sections through streamlined dies [J]. Trans ASME; J Eng Industry, 1985, 107: 229-233.
[9] HAN C H, YANG D Y, KIUCHI M. A new formulation for three-dimensional extrusion and its application to extrusion of clover sections [J]. Int J Mech Sci, 1986, 28(4): 201-218.
[10] YANG D Y, HAN C H, KIM M V. A generalized method for analysis of three-dimensional extrusion of arbitrarily-shaped sections [J]. J Mech Sci, 1986, 28(8): 517-534.
[11] LEE R S, SHEU J J, GAU Y J. Optimum die-surface design of gear-spline extrusions using a general surface model [J]. J Mat Proc Tech, 1991, 28: 365-382.
[12] SHEU J J, LEE R S. Optimum die surface design of general three-dimensional section extrusions by using a surface model with tension parameter [J]. Int J Mach Tools & Manuf, 1991, 31(4): 521-537.
[13] MAITY K P, KAR P K, DAS N S. A class of upper-bound solutions for the extrusion of square shapes from square billets through curved dies [J]. J Mat Proc Tech, 1996, 62: 185-190.
[14] WIFI A S, SHATLA M N, ABDEL-HAMID A. An optimum-curved die profile for the hot forward rod extrusion process [J]. J Mat Proc Tech, 1998, 73: 97-107.
[15] SAHOO S K, KAR P K, SINGH K C. A numerical application of the upper-bound technique for round-to-hexagon extrusion through linearly converging dies [J]. J Mat Proc Tech, 1999, 91: 105-110.
[16] SHEU J J. A three-dimensional CAD/CAM/CAE integration system of sculpture surface die for hollow cold extrusion [J]. Int J Mach Tools & Manuf, 1999, 39: 33-53.
[17] ONUH S O, EKOJA M, ADEYEMI M B. Effects of die geometry and extrusion speed on the cold extrusion of aluminium and lead alloys [J]. J Mat Proc Tech, 2003, 132: 274-285.
[18] NOORANI M, JOOYBARI M B, HOSSEINIPOUR S J, GORJI A. Experimental and numerical study of optimal die profile in cold forward rod extrusion of aluminum [J]. J Mat Proc Tech, 2005, 164-165: 1572-1577.
[19] AJIBOYE J S, ADEYEMI M B. Upper bound analysis of die land length in cold extrusion [J]. J Mat Proc Tech, 2006, 177(1-3): 608-611.
[20] JOOYBARI M B, SABOORI M, NOORANI-AZAD M, HOSSEINIPOUR S J. Combined upper bound and slab method, finite element and experimental study of optimal die profile in extrusion [J]. Mat & Des, 2007, 28(6): 1812-1818.
[21] GORDON W A, van TYNE C J, MOON Y H. Axisymmetric extrusion through adaptable dies—Part 1: Flexible velocity fields and power terms [J]. Int J Mech Sci, 2007, 49: 86-95.
[22] GORDON W A, van TYNE C J, MOON Y H. Axisymmetric extrusion through adaptable dies—Part 2: Comparison of velocity fields [J]. Int J Mech Sci, 2007, 49: 96-103.
[23] GORDON W A, van TYNE C J, MOON Y H. Axisymmetric extrusion through adaptable dies—Part 3: Minimum pressure streamlined die shapes [J]. Int J Mech Sci, 2007, 49: 104-115.
[24] ALTINBALIK T, AYER  . A theoretical and experimental study for forward extrusion of clover sections [J]. Materials & Design, 2008, 29(6): 1182-1189.
. A theoretical and experimental study for forward extrusion of clover sections [J]. Materials & Design, 2008, 29(6): 1182-1189.
[25] ALTINBALIK T, AYER  . A theoretical study for optimum die length for forward extrusion of clover sections from circular billets through curved dies [C]. UNITECH’09 International Scientific Conference. Gabrovo: Technicd University of Gabrovo, Vol. 2, 2009: 160-165.
. A theoretical study for optimum die length for forward extrusion of clover sections from circular billets through curved dies [C]. UNITECH’09 International Scientific Conference. Gabrovo: Technicd University of Gabrovo, Vol. 2, 2009: 160-165.
[26] HUANG G M, WANG J P, LEE H D, CHANG C S. Rigid-plastic boundaries approach to the analysis of arbitrary profile dies in axisymmetric extrusion [J]. J Mat Proc Tech, 2009, 209: 4351-4359.
[27] ALTINBALIK T, AYER  . FEM simulation and die transition profile optimization of extrusion process of clover sections [C]// IMEF’12 Pragur: Pragur Czech University of life Sciences, 2012: 92-105.
. FEM simulation and die transition profile optimization of extrusion process of clover sections [C]// IMEF’12 Pragur: Pragur Czech University of life Sciences, 2012: 92-105.
Tahir ALTINBALIK, Onder AYER
Department of Mechanical Engineering, Faculty of Engineering and Architecture, Trakya University, 22180 Edirne, Turkey
摘 要:对模具入口、过渡区几何形状对挤压载荷和材料流动的影响进行了理论和实验研究。选取的模具形状有4种,分别为截面为圆形、四叶草形的直锥模,截面为圆形、四叶草形的余弦弯模。工业纯铅因其室温热变形能力强而被选作实验材料。根据上限分析法,提出一个新的运动许可速度场来分析四叶草形模具挤压圆坏得到的压件形状。理论分析得到的不同模具入口、过渡区几何形状挤压载荷与实验结果一致。以挤压件的轴向偏差来衡量产品质量尺寸方面的好坏。
关键词:挤压;四叶草形状;上限分析法;最佳模具形状
(Edited by Hua YANG)
Corresponding author: Tahir ALTINBALIK; Tel: +90-284-226 1217; Fax: +90-284-226 1225; E-mail: tahira@trakya.edu.tr
DOI: 10.1016/S1003-6326(13)62571-6

