文章编号：1004-0609(2007)07-1063-09
扩容角对初始随机材料缺陷岩石试样破坏过程及力学行为的影响
王学滨
(辽宁工程技术大学 力学与工程科学系，阜新 123000)
摘 要：在单轴平面应变压缩条件下，采用FLAC模拟扩容角对具有初始随机材料缺陷的光滑端面岩石试样的破坏过程及对应力—应变曲线的影响。利用FISH函数于试样内部规定初始缺陷。密实的岩石服从莫尔库仑剪破坏与拉破坏复合的破坏准则，破坏之后呈现应变软化-理想塑性行为。缺陷在破坏之后经历理想塑性行为。扩容角较高时试样内部最终发生破坏的单元数目较多。随着扩容角的增加，剪切带变得粗壮和陡峭。扩容角对应力—轴向应变曲线影响不大。扩容角增加时，在应变软化阶段，应力—侧向应变曲线变平缓，根据作者过去提出的理论公式，这是由于剪切带宽度增加的贡献超过剪切带倾角增加的贡献所致。当扩容角较高时，应力峰值时试样内部的最大剪切应变增量较高，因而试样破坏的前兆比较明显。剪切带倾角的数值结果与Arthur倾角比较接近，未能超过Coulomb倾角。扩容角越大，剪切带最终可以获得越来越高的剪切应变和体积应变。
关键词：非均质性；材料缺陷；扩容角；剪切带；轴向应变；侧向应变；前兆
中图分类号：TU 451 文献标识码：A
Effects of dilation angle on failure process and mechanical behavior for rock specimen with random material imperfections
WANG Xue-bin
(Department of Mechanics and Engineering Sciences, Liaoning Technical University, Fuxin 123000, China)
Abstract: For rock specimen with smooth ends and with initially random material imperfections, the effects of dilation angle (DA) on the failure process and stress—strain curve were numerically modeled using FLAC in uniaxial plane strain compression. Using a written FISH function, the initial imperfections within the specimen were prescribed. For intact rock exhibiting linear strain-softening behavior beyond the occurrence of failure and then ideal plastic behavior, the failure criterion is a composite Mohr-Coulomb criterion with tension cut-off. Initial imperfection undergoes ideal plastic behavior beyond the occurrence of failure. Rock specimen with higher DA is subjected to severe failure in the final deformation stage. Wider and steeper shear bands are observed at higher DA. The effects of DA on the stress—axial strain curve can be neglected. Less steep stress—lateral strain curve at post-peak is expected at higher DA since the contribution of the increase in shear band width to lateral strain exceeds the contribution of the increase in shear band inclination according to an analytical expression proposed by Wang and coworkers. Higher DA leads to higher value of maximum shear strain increment within the specimen. Therefore, more apparent precursor to failure can be observed at higher DA. Shear band inclination is closer to Arthur theory and is lower than Coulomb theory. Higher DA results in higher values of shear strain and volumetric strain in shear band.
Key words: heterogeneity; material imperfections; dilation angle; shear band; axial strain; lateral strain; precursor
岩石属于典型的非均质材料。在压缩载荷作用下，微裂纹可以出现在材料缺陷(如孔洞、孔隙或裂纹)附近。考虑非均质性，一些研究人员已采用数值方法模拟了岩石的破坏过程和宏观力学行为[1-2]。通常，采用威布尔分布函数描述单元强度的随机变化。在数值模拟中，广泛采用峰后脆-塑性的本构关系，未考虑相对复杂的峰后应变软化-塑性的本构关系。而且，所有的单元具有不同的强度，因而，难于研究具有初始随机材料缺陷的岩样的破坏过程及宏观力学行为。
拉格朗日元法(FLAC)是一个显式的有限差分程序，可以有效地模拟地质体材料的屈服极限被达到之后的塑性流动行为。FLAC的一个突出特点是包含了一个强有力的内嵌的编程语言FISH。FISH允许用户定义新的变量、函数和本构模型。
最近，王学滨[3-5]编制了计算平面应变压缩岩样全部变形特征(轴向应变、侧向应变、体积应变、由侧向应变及轴向应变计算得到的泊松比)的FISH函数，分别研究了软化模量(峰后脆性)、扩容角、初始粘结力及内摩擦角对平面应变单轴压缩状态下含单一材料缺陷岩样的破坏过程、模式、前兆及全部变形特征的 影响。
本文作者利用FLAC模拟了扩容角对具有初始随机材料缺陷的岩样的破坏过程、破坏模式、应力—轴向应变曲线、应力—侧向应变曲线及破坏前兆的影响。利用Matlab软件生成了在试样内部规定初始缺陷的FISH函数。
1 本构关系及计算模型
计算模型的几何尺寸、单元划分及边界条件如图1所示。试样的高度及宽度分别为10 cm和5 cm。试样两端面是光滑的，在试样的上端面施加常速度v= 5×10-10 m/时间步，计算在小变形模式及平面应变状态下进行。将试样划分为若干正方形单元，单元边长为1.25 mm。
共选择4个计算方案。方案1至4的扩容角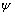
分别为5?、15?、25?及35?。方案1至4的差别仅在于扩容角不同，初始随机材料缺陷分布相同，见图1。黑色单元代表材料缺陷，白色单元代表密实的岩石。
在弹性阶段，密实岩石和材料缺陷有相同的本构关系，弹性模量取为26.6 GPa，泊松比取为0.21。
材料缺陷发生破坏之后经历理想塑性行为，材料缺陷的粘结力和内摩擦角分别为0.1 MPa及38?。
密实岩石一旦发生破坏先是经历线性应变软化行为，然后是理想塑性行为。密实岩石的破坏准则选取莫尔库仑剪破坏与拉破坏复合的模型，抗拉强度取为0.2 MPa。密实岩石发生破坏之后的粘结力、内摩擦角与塑性应变的关系见图2，初始(塑性应变为零时)粘结力取为0.275 MPa，初始内摩擦角取为44?。
图1 模型的几何特征及边界条件
Fig.1 Model geometry and boundary conditions
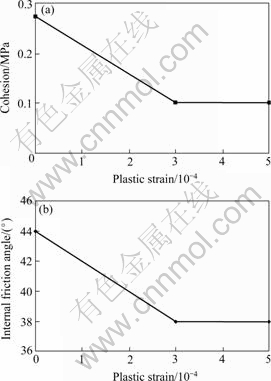
图2 材料缺陷之外的密实岩石的峰后本构关系
Fig.2 Post-peak constitutive relation for intact rock outside imperfections
2 规定试样初始缺陷的FISH 函数
为了在试样内部规定初始缺陷，需要执行下列3步。
1) 抽取随机数：在1~3 200(单元的最大数)之间按均匀分布抽取随机数300次。
2) 记住识别号码：让被抽取到的随机数等于FLAC中的识别号码，记住每个识别号码。在FLAC中，每个单元都有一个识别号码。在本文中，识别号码的最小值和最大值分别是1和3 200。
3) 赋予本构关系：将被记住的识别号码所对应的单元(材料缺陷)赋予理想塑性本构关系，而将其余的识别号码所对应的单元(密实的岩石)先是赋予线性应变软化的本构关系，然后是理想塑性本构关系。这一步骤是在给密实的岩石和材料缺陷赋予相同的弹性本构关系之后进行的。
上述过程是利用Matlab生成FLAC可以识别的FISH函数实现的。
应当指出，在方案1~4中，材料缺陷的最大数目为300。这是由于在1~3 200中随机抽取300次随机数(两次或多次可能抽到相同的随机数)，因而，材料缺陷的实际数目可能小于300。
3 计算结果及分析
3.1 图例说明
图3~6所示分别为方案1~4的破坏过程及宏观应力—轴向应变曲线。黑色单元表示这些单元已经发生了剪切或拉伸破坏；白色单元表示这些单元尚处于弹性状态。
图7(a)和(b)所示分别为每个方案的应力—轴向应变曲线及应力—侧向应变曲线。轴向应变εa定义为[3-4]
t是时步。式(1)中εa为正，表示岩样在压缩过程中轴向的缩短。由各图片的时间步，很容易由式(1)计算出试样此时的轴向应变εa。以图3为例，图3(a)与图3(i)中a点对应，图3(b)与图3(i)中b点对应，以此类推。
本文中的侧向应变εl是平均侧向应变，它的计算公式为[3-4]
ui-vi是具有相同高度的节点的水平方向相对位移，将其求和后除以节点数n为水平方向平均相对位移。水平方向平均相对位移再除以岩样的宽度B为水平方向平均侧向应变εl。式(2)中εl为负，表示岩样在压缩过程中侧向的膨胀。
图8(a)~(d)分别给出了4个方案当应变软化行为刚发生时的剪切带图案(剪切应变增量等值线图)。图8(a)~(d)中横坐标上的数字(1~40)及纵坐标上的数字(1~80)分别表示在水平及垂直方向上的各个单元。
图9(a)~(d)分别给出了4个方案当时间步达到 12 000时的剪切带图案。图9仍是剪切应变增量等值线图。
图10(a)~(d)分别给出了4个方案当时间步达到 12 000时的剪切带图案。图10所示是体积应变增量等值线图。
3.2 具有初始随机材料缺陷岩样的一般破坏过程
首先，几个缺陷发生破坏，并且在轴向得到一定程度的长大。然后，许多缺陷相继破坏，在轴向有限长大，它们之间相互竞争，处于无序的状态之中。接下来，一些屈服的单元聚结，形成了较短的剪切破裂带(简称为剪切带)。最终，一些短剪切带联结成有序的、倾斜的、贯通试样的宏观长剪切带。
3.3 不同扩容角时试样破坏过程的差异
由图3~6(a)，当时间步达5 000时，不同扩容角时试样的破坏形态(破坏单元在试样内部的分布规律)没有明显的差别。
随着轴向应变的增加，见图3~6(b)~(d)，扩容角高时试样内部发生破坏的单元数目多。
当应力—轴向应变曲线达到峰值之后，该曲线呈现应变软化状态，试样的破坏形态基本不再改变，破坏的单元数目基本不再增加。扩容角高时试样内部最终发生破坏的单元数目多，见图3~6(f)~(h)。扩容角高时倾斜的剪切带较陡峭，剪切带与水平方向的夹角(剪切带倾角)较高。而且，扩容角高时剪切带较粗壮。也就是说，扩容角高时剪切带较宽。这一点与文献[4, 6-7]的数值结果是一致的。
基于剪切应变梯度塑性理论，文献[8]提出了考虑
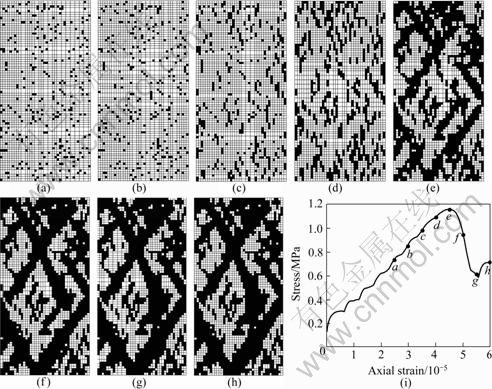
图3 方案1(ψ=5?)的破坏过程(a~h)及宏观应力—轴向应变曲线(i)
Fig.3 Failure process (a-h) and macroscopic stress—axial strain curve (i) for scheme 1 (ψ=5?): (a) 5 000; (b) 6 000; (c) 7 000; (d) 8 000; (e) 9 000; (f) 10 000; (g) 11 000; (h) 12 000 timesteps
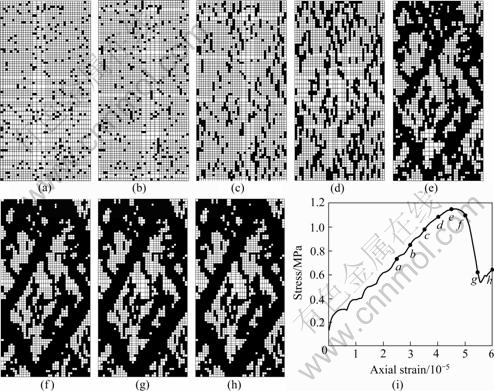
图4 方案2(ψ=15?)的破坏过程(a~h)及宏观应力—轴向应变曲线(i)
Fig.4 Failure process (a-h) and macroscopic stress—axial strain curve (i) for scheme 2 (ψ=15?): (a) 5 000; (b) 6 000; (c) 7 000; (d) 8 000; (e) 9 000; (f) 10 000; (g) 11 000; (h) 12 000 timesteps
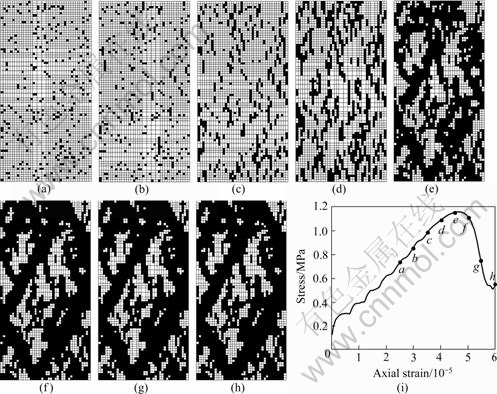
图5 方案3(ψ=25?)的破坏过程(a~h)及宏观应力—轴向应变曲线(i)
Fig.5 Failure process (a-h) and macroscopic stress—axial strain curve (i) for scheme 3 (ψ=25?): (a) 5 000; (b) 6 000; (c) 7 000; (d) 8 000; (e) 9 000; (f) 10 000; (g) 11 000; (h) 12 000 timesteps
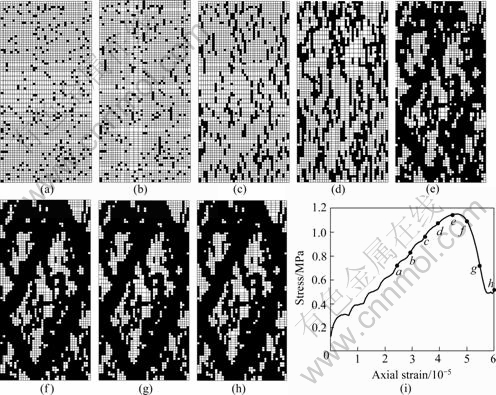
图6 方案4(ψ=35?)的破坏过程(a~h)及宏观应力—轴向应变曲线(i)
Fig.6 Failure process (a-h) and macroscopic stress—axial strain curve (i) for scheme 4(ψ=35?): (a) 5 000; (b) 6 000; (c) 7 000; (d) 8 000; (e) 9 000; (f) 10 000; (g) 11 000; (h) 12 000 timesteps
剪胀后的剪切带厚度w的理论公式：w=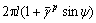 
，其中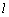
是内部长度，
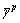是平均塑性剪切应变。由此可见，随着ψ的增加，w增加。因此，本文的数值结果是可信的。
3.4 不同扩容角时试样宏观轴向力学行为的差异
图7(a)表明，扩容角对应力—轴向应变曲线(包括峰值应力、峰值应力所对应的轴向应变及应力—轴向应变曲线的峰后斜率)影响甚微。方案1~4的峰值应力的计算结果分别为1.131、1.137、1.141及1.14 MPa。应变软化行为刚发生时的时间步分别为9 130、9 340、9 400及9 390。
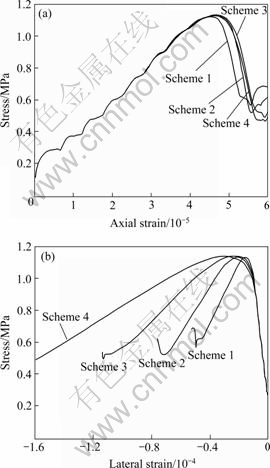
图7 方案1~4的应力—轴向应变曲线(a)及应力—侧向应变曲线(b)
Fig.7 Stress—axial strain(a) and stress—lateral strain(b) curves for schemes 1-4
单轴压缩岩样发生单一剪切破坏时，文献[9]得到了应变软化阶段应力—轴向应变曲线的斜率的解析解。该斜率受剪切带倾角及宽度影响。剪切带倾角增加使该曲线软化段变得陡峭，剪切带宽度增加使该曲线软化段变得平缓。
本文的数值结果表明，扩容角增加时，剪切带倾角及宽度均增加。扩容角增加时，软化阶段应力—轴向应变曲线是变得平缓还是变得陡峭取决于剪切带倾角及宽度二者之间谁的作用效果更明显。本文的数值结果表明，扩容角增加时，软化阶段应力—轴向应变曲线的斜率基本不改变，这意味着剪切带倾角及宽度增加对轴向应变的作用效果相互抵消。
3.5 不同扩容角时试样宏观侧向力学行为的差异
图7(b)表明，扩容角较高时的应力—侧向应变曲线软化段较平缓。在相同的承载能力时，具有较高扩容角的试样可以获得较高的侧向应变。
单轴压缩岩样发生单一剪切破坏时，文献[10]得到了应变软化阶段应力—侧向应变曲线的斜率的解析解。该斜率受剪切带倾角及宽度影响。剪切带倾角增加使软化段曲线变得陡峭，剪切带宽度增加使软化段曲线变得平缓。
本文的数值结果表明，扩容角增加时，剪切带倾角及宽度均增加；而且，在应变软化阶段，扩容角较高时应力—侧向应变曲线较平缓，这意味着剪切带宽度增加的作用效果已经超过了剪切带倾角增加的作用效果。
3.6 不同扩容角时试样破坏前兆的差异
当应变软化行为刚发生时(见图8)，在试样内部可以观测到若干较短的倾斜的剪切带，剪切带网络的格局比较明显。这些剪切带可以视为试样破坏的前兆。
当应变软化行为刚发生时，方案1~4的最大剪切应变增量逐渐增加。因此，扩容角较高时试样破坏的前兆更明显，这一结果与文献[4]的结果类似。
扩容角较高时，较短的剪切带较陡峭；而且，在试样内部可以观测到一些较短的近乎与轴向平行的剪切应变集中区域，见图8(c)~(d)。这一现象也可在图9(c)~(d)中发现。
3.7 不同扩容角时试样最终破坏模式的差异
对于方案1，最终在试样内部可以观测到3条剪切带(见图9)。对于方案2~4，最终在试样内部均可以观测到4条剪切带。剪切带明显随着扩容角的增加而变得粗壮和陡峭。
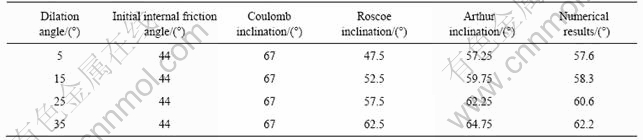
下面以靠近试样左下角的剪切带为例，阐述扩容角不同时剪切带倾角的变化规律。通过测量，方案1~4的该剪切带的倾角分别为57.6?、58.3?、60.6?及62.2?。由此可见，随着扩容角的增加，剪切带倾角有增加的趋势。Coulomb倾角公式(仅考虑摩擦角)[11-12]对此不能解释。在定性上，Roscoe倾角公式(仅考虑扩容角)及Arthur倾角公式(考虑摩擦角和扩容角)[11-12]与上述数值结果是一致的。
接下来，将剪切带倾角的数值结果与若干剪切带倾角公式的预测结果进行定量的比较，结果见表1。初始内摩擦角为密实岩石的初始内摩擦角。可以发现，剪切带倾角的数值结果未能超过Coulomb倾角；数值结果与Arthur倾角比较接近；通常，Roscoe倾角低于剪切带倾角的数值结果，除非扩容角较高时。
由图9和图10可见，剪切应变增量等值线图与体积应变增量等值线图具有一定的相似性。由体积应变增量等值线图也可以发现剪切带明显随着扩容角的增加而变得粗壮和陡峭。
对于方案1，剪切带位置的体积应变具有一定程度的集中(见图10(a))，剪切带之外的一些位置也具有一定程度的体积应变集中。剪切带的背景不太清晰，剪切带内部的体积应变与带外的体积应变的差别不十分显著。
对于方案4，基本上只有剪切带位置的体积应变才具有一定程度的集中(见图10(d))，剪切带之外的位置基本上不具有体积应变集中。剪切带的背景一片空白，剪切带内部的体积应变与带外的体积应变的差别十分显著，二者的对比十分鲜明。
当时间步达到12 000时，方案1~4的最大剪切应变增量逐渐增加。当时间步达到12 000时，方案1~4的最大体积应变增量也逐渐增加。因此，扩容角越高，剪切带最终可以获得越来越高的剪切应变和体积应变。
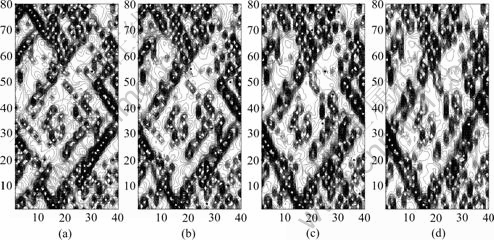
图8 当应变软化行为刚发生时方案1~4的剪切应变增量
Fig.8 Shear strain increments of schemes 1-4 when strain-softening behavior just occurs: (a) Scheme 1; (b) Scheme 2; (c) Scheme 3; (d) Scheme 4
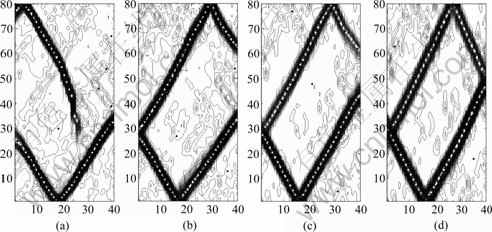
图9 当时间步达到12 000时方案1~4的剪切应变增量
Fig.9 Shear strain increments of schemes 1-4 at 12 000 timesteps: (a) Scheme 1; (b) Scheme 2; (c) Scheme 3; (d) Scheme 4
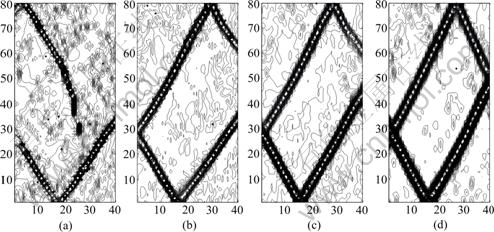
图10 当时间步达到12 000时方案1~4的体积应变增量
Fig.10 Volumetric strain increments of schemes 1-4 at 12 000 timesteps: (a) Scheme 1; (b) Scheme 2; (c) Scheme 3; (d) Scheme 4
表1 Coulomb, Roscoe及Arthur倾角公式的计算结果及本文的数值结果
Table 1 Predictions according to Coulomb, Roscoe and Arthur’s inclination and present numerical results
4 结论
1) 扩容角较高时试样内部最终发生破坏的单元数目较多。随着扩容角的增加，剪切带变得粗壮和陡峭。
2) 扩容角对应力—轴向应变曲线影响不大。在应变软化阶段，剪切带宽度增加对轴向应变的作用效果与剪切带倾角增加的作用效果相当。
3) 扩容角增加时，在应变软化阶段，扩容角较高时的应力—侧向应变曲线较平缓。这意味着剪切带宽度增加的作用效果已经超过了剪切带倾角增加的作用效果。
4) 当扩容角较高时，试样破坏的前兆比较明显；在应变软化行为刚发生时，除了可以在试样内部观测到倾斜的较短的剪切带，还可观测到一些较短的近乎与轴向平行的剪切应变局部化区。
5) 剪切带倾角的数值结果未能超过Coulomb倾角；数值结果与Arthur倾角比较接近；通常，Roscoe倾角低于剪切带倾角的数值结果，除非扩容角较高时。
6) 若扩容角大于零，剪切应变增量与体积应变增量等值线图具有一定的相似性。扩容角越大，剪切带最终可以获得越来越高的剪切应变和体积应变。
REFERENCES
[1] Fang Z, Harrison J P. Development of a local degradation approach to the modeling of brittle fracture in heterogeneous rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(4): 443-457.
[2] Tang C A, Kou S Q. Crack propagation and coalescence in brittle materials under compression[J]. Engineering Fracture Mechanics, 1998, 61(3/4): 311-324.
[3] 王学滨. 软化模量对岩样全部变形特征的影响[J]. 岩土工程学报, 2006, 28(5): 600-605.
WANG Xue-bin. Effect of softening modulus on entire deformational characteristics of rock specimen[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(5): 600-605.
[4] 王学滨. 剪胀对岩样全部变形特征的影响[J]. 四川大学学报(工程科学版), 2005, 37(5): 25-30.
WANG Xue-bin. Effects of shear dilatancy on entire deformational characteristics of rock specimen[J]. Journal of Sichuan University (Engineering Science Edition), 2005, 37(5): 25-30.
[5] 王学滨. 初始内聚力及摩擦角对岩样全部变形特征的影响[J]. 沈阳建筑大学学报(自然科学版), 2005, 21(5): 472-477.
WANG Xue-bin. Effects of initial cohesions and friction angles on entire deformational characteristics of rock specimen [J]. Journal of Shenyang Jianzhu University (Natural Science), 2005, 21(5): 625-629.
[6] Hobbs B E, Ord A. Numerical simulation of shear band formation in a frictional-dilatational material[J]. Ingenigeur- Archiv, 1989,59(2): 209-220.
[7] 王学滨, 潘一山, 盛 谦, 丁秀丽. 平面应变岩样局部化变形场数值模拟研究[J]. 岩石力学与工程学报, 2003, 22(4): 521-524.
WANG Xue-bin, PAN Yi-shan, SHENG Qian, DING Xiu-li. Numerical simulation of localized deformation field for rock in plane strain state[J]. Chinese Journal of Rock Mechanics and Engineering, 2003,22(4): 521-524.
[8] WANG Xue-bin, TANG Ju-peng, ZHANG Zhi-hui, PAN Yi-shan. Analysis of size effect, shear deformation and dilation in direct shear test based on gradient-dependent plasticity [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(7): 1095-1099.
[9] WANG Xue-bin. Analytical solution of complete stress—strain curve in uniaxial compression based on gradient-dependent plasticity[C]//Eurock 2005-Impact of Human Activity on the Geological Environment. London: Taylor & Francis Group, 2005: 661-667.
[10] 王学滨, 刘 杰, 王 雷, 潘一山. 基于梯度塑性本构理论的岩样侧向变形分析(Ⅱ): 尺寸效应及弹性会跳[J]. 岩土力学, 2004, 25(7): 1127-1130.
WANG Xue-bin, LIU Jie, WANG Lei, PAN Yi-shan. Analysis of lateral deformation of rock specimen based on gradient- dependent plasticity (Ⅱ): Size effect and snap-back[J]. Rock and Soil Mechanics, 2004, 25(7): 1127-1130.
[11] Vardoulakis I. Shear band inclination and shear modulus of sand in biaxial tests[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1980, 4(2): 103-119.
[12] Vermeer P A. The orientation of shear bands in biaxial tests[J]. Géotechnique, 1990, 40(2): 223-236.
(编辑 袁赛前)
基金项目：国家自然科学基金资助项目(50309004)
收稿日期：2006-10-17；修订日期：2007-03-06
通讯作者：王学滨，副教授，博士；电话：0418-3350924; E-mail: wxbbb@263.net
