改进规则下自适应神经网络的UUV水平面路径跟随控制
周佳加1,严浙平1,贾鹤鸣2,侯恕萍3
(1. 哈尔滨工程大学 自动化学院,黑龙江 哈尔滨,150001;
2. 东北林业大学 机电工程学院,黑龙江 哈尔滨,150040;
3. 哈尔滨工程大学 机电工程学院,黑龙江 哈尔滨,150001)
摘要:为实现无人水下航行器(UUV)在水动力参数变化和外界不确定干扰下的水平面路径跟随控制,提出一种基于Lyapunov方法的自适应神经网络控制方法。针对直线段航路交接处减速拐弯时位置控制精度较差的问题, 提出利用圆弧连接的圆弧段路径的航向制导(LOS)来改进单纯直线段连接的航向制导,降低拐点处的跟踪误差。引入RBF神经网络来估计误差和海流干扰,设计自适应学习律来保证神经网络权值的最优估计,保证系统的位置误差和艏向误差收敛到零。仿真试验结果表明:设计的控制器在路径跟随过程中可有效抑制UUV载体的模型不确定性,对外界海流干扰有较好的抑制作用,且控制参数易于调节。
关键词:无人水下航行器;路径跟随;航向制导律;自适应神经网络
中图分类号:TP24 文献标志码:A 文章编号:1672-7207(2014)09-3021-08
Improved path-following in horizontal plane for UUV using adaptive neural network controller
ZHOU Jiajia1, YAN Zheping1, JIA Heming2, Hou Shuping3
(1. College of Automation, Harbin Engineering University, Harbin 150001, China;
2. College of Mechanical and Electrical Engineering, Northeast Forestry University, Harbin 150040, China;
3. College of Mechanical and Electrical, Harbin Engineering University, Harbin 150001, China)
Abstract: In order to deal with the parameter variations and uncertainties during path following control with unmanned underwater vehicles, an adaptive neural network controller was designed using Lyapunov stability analysis. In order to eliminate the cross track error near the intersection which is a connection of two straight lines, an improved LOS law was proposed using straight lines linked with arcs. For the estimation error and current disturbance, the RBF neural network (NN) was introduced to estimate unknown terms where an adaptive law was chosen to guarantee optimal estimation of the weight of NN, when meanwhile a virtual control input was introduced to ensure that the system error, including position error and heading error, can be converged to 0. Simulation results demonstrate that the proposed controller, whose parameters can be set easily, is effective to eliminate the disturbances caused by vehicle’s nonlinear and model uncertainty, and can overcome current.
Key words: unmanned underwater vehicle; path-following; line-of-sight (LOS); adaptive neural network
无人水下航行器(unmanned underwater vehicle,UUV)的水平面路径跟随能力是实现其水下管道检测、海底地形勘测和打捞施工的重要技术前提[1-4]。实际中,待检测海底管道、电缆及海底地形等静态目标常常认为可用一系列直线段的集合来近似,此时,相邻直线段的交角可能为锐角、直角或者钝角。这意味着当UUV在相邻直线段运动时,跟随目标将发生跳变,系统状态也极有可能朝着发散的方向发展。为了保证检测的可靠性,要求携带观测设备的载体在指定高度、准确的水平面位置航行,因此,减速转弯是实现准确路径跟随的措施之一,其可有效地减小转弯时航向的超调。但是,当UUV浮力与重力不均衡时,UUV一旦减速,随着舵效的降低,其深度将会有明显变化,即深度控制能力降低。另外,在不同的航行环境中[5-6],UUV的水动力参数是变化的,很难精确地估计水动力参数的先验值,加之外界海流干扰的影响,使得UUV在航道改变过程中既满足深度或高度控制精度,又降低转弯引起的水平面位置误差成为亟需解决的工程难题。目前,在解决UUV的运动控制中,大部分方法集中在控制器设计方面去求解。毕凤阳等[7]为了实现具有时变水动力系数、未建模动态和时滞等不确定性的欠驱动无人水下航行器的鲁棒控制,以变结构控制的切换函数及其变化率为模糊控制器的输入,以变结构控制律的变化率为模糊控制器的输出设计了一个模糊变结构控制器。但是,该控制器在目标跟踪状态发生变化时有抖振现象。施淑伟等[8]针对欠驱动AUV(autonomous underwater vehicle)在常值海流影响下的水平面路径跟踪控制问题,建立了常值海流作用下的AUV运动学和动力学模型,并采用以自由参考点为原点的Serret-Frenet坐标系描述路径跟踪误差及其动态模型,综合应用李亚普诺夫方法和反步法设计了AUV路径跟踪的运动学和动力学控制律,水平面跟踪控制效果较为理想,但是,从其速度变化曲线可发现在轨迹跟踪开始后的18 s左右载体的横向速度大于纵向运动速度,实际中这将影响欠驱动无人水下航行器的水平面运动稳定性,载体容易发生侧滑而引起航行器失控[8]。上述研究单纯从控制器角度设计UUV水平面运动控制器,并未考虑制导规则在运动控制问题中的重要性。对UUV在水平面的运动分析知,该机动问题可分为2个子问题:一方面为几何学问题,即利用设计的制导律和控制器使UUV的运动到预先规划的路径上;另一方面为动力学问题,即使UUV的前向速度保持在设计航速。对于前者,本文利用Line-of-Sight(LOS)系统[9-11]将期望位置(xd, yd)映射到指令航向角,并通过设计的自适应神经网络控制器[12-15](adaptive NN controller,即ANNC)解算控制量实现载体的水平面路径跟随控制,执行机构为方向舵。ANNC采取RBF神经网络估计不确定项,选用合适的自适应律来保证神经网络权值的最优估计使得估计更加精确。同时,为了便于设计ANCC控制器,将UUV的水平面动力学特性简化为一个非仿射纯反馈系统,并通过恰当的选择设计参数保证闭环系统的控制性能。基于李亚普诺夫稳定性定理,该控制器可以保证路径跟随控制系统中的误差状态是渐近稳定的,使得系统输出收敛到临近设定路径的很小范围内。对于后者,利用主推进器实现载体航速控制。
1 UUV水平面运动模型
由刚体动力学角度分析,UUV在水平面运动控制问题就是解决其在该平面内的三自由度路径跟随控制。本文研究的UUV在水平面机动时利用主推进器来提供纵向推力,方向舵用于实现航向控制,即控制输入维数少于系统维数,属于欠驱动UUV。另外,当全驱动水下无人航行器前向运动速度较高时,横向推进器推力对载体的作用被弱化,即在高速时其表现出欠驱动特性。因此,研究欠驱动条件约束下的UUV在水平面的路径跟随控制有重要意义[4, 9]。
本文所研究的UUV长×宽×高为6.77 m×1.98 m×1.72 m,如图1所示。UUV重心与船体坐标系的原点一致。该UUV在oxy平面上沿纵轴对称地装有2个主推进器;利用艉部十字舵不同控制面进行机动航行,水平面机动时方向舵舵角的转动约束为±30°。设定UUV的最大对流速度是6节(约3.08 m/s)。

图1 UUV坐标系
Fig. 1 Earth-fixed and body-fixed coordinate systems
结合UUV载体的结构特性,描述其水平面路径跟随控制的简化的运动方程可如式(1)~(4)所示。
载体动力学:

 (1)
(1)
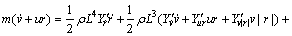
 (2)
(2)

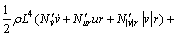
 (3)
(3)
载体运动学:
 (4)
(4)
其中:L,m和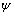 分别为UUV的长度、质量和艏向角;Iz为转动惯量;u,v和r为在船体坐标系中的平移速度和角速度;
分别为UUV的长度、质量和艏向角;Iz为转动惯量;u,v和r为在船体坐标系中的平移速度和角速度; ,
,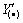 和
和 为无因次水动力系数;
为无因次水动力系数; 和
和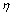 为UUV重心在固定坐标系中的位置;
为UUV重心在固定坐标系中的位置; 为海水密度;
为海水密度; 为方向舵舵角的偏转角度;
为方向舵舵角的偏转角度;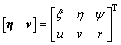 ;
; 。
。
2 水平面LOS航行制导律
在载体纵向运动航速可控的情况下,欲实现UUV在水平面的机动即为了解决几何学问题,下面将从LOS航向制导律和自适应神经网络路径跟随控制器2方面对其进行设计,最终得到带约束的自适应神经网络水平面路径跟随控制器。
2.1 直线段路径的LOS航向制导律
假设在水平面UUV的航行速度可表示为

此时,与航行机动相关的航迹角为
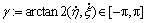
已知约束为平面内的预规划的路径,要使UUV跟随到指定位置,则需要研究与路径相关的航行制导律以及控制载体的运动速度。若规划的路径可通过一系列点连接表示 ,其中
,其中 ,则取跟随路径上2点pk和pk+1,并以pk为原点,沿路径方向建立路径坐标系{p},如图2所示。
,则取跟随路径上2点pk和pk+1,并以pk为原点,沿路径方向建立路径坐标系{p},如图2所示。
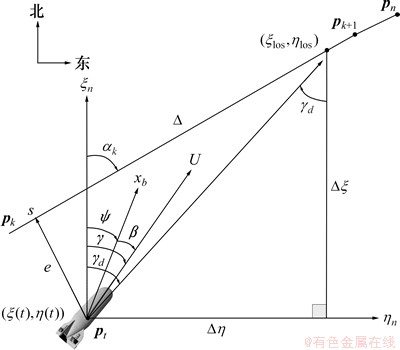
图2 LOS航向制导律原理图
Fig. 2 Principle of LOS guidance for straight-lines in horizontal plane
由图2可知:沿路径方向建立的坐标系{p}的x轴与大地坐标系北向的夹角为
 (5)
(5)
此时,可在路径坐标系{p}中描述运动载体的坐标:

 (6)
(6)
其中: 为UUV当前点坐标;
为UUV当前点坐标; ,称s(t)为径向跟随误差,e(t)为横向跟随误差。对于路径跟随问题,若e(t)=0便意味着UUV渐近运动至设定的路径,因此,e(t)为实现路径跟随的关键设计因素。考虑水平面内UUV的路径跟随控制,欲实现目标
,称s(t)为径向跟随误差,e(t)为横向跟随误差。对于路径跟随问题,若e(t)=0便意味着UUV渐近运动至设定的路径,因此,e(t)为实现路径跟随的关键设计因素。考虑水平面内UUV的路径跟随控制,欲实现目标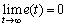 ,可利用UUV控制系统中航速控制和航向控制的组合达到。
,可利用UUV控制系统中航速控制和航向控制的组合达到。
将建立路径坐标系{p}的想法推进一步,即假设在跟随路上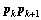 有1个移动前向点
有1个移动前向点

 ,且该点距离载体在直线段
,且该点距离载体在直线段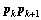 的投影点的距离
的投影点的距离 ,其中n=2~5,称
,其中n=2~5,称 为前视向量。根据图2知:依赖于前视向量的航向制导律为
为前视向量。根据图2知:依赖于前视向量的航向制导律为
 (7)
(7)
其中:当规划路径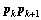 给定时,
给定时, 为常值;而
为常值;而 类似饱和比例关系,将横向跟随误差
类似饱和比例关系,将横向跟随误差 映射到
映射到 ,正是这种饱和特性可有效限制载体渐近跟随至路径
,正是这种饱和特性可有效限制载体渐近跟随至路径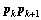 的速度。
的速度。
2.2 圆弧段路径的LOS航向制导律
参考直线段路径的LOS航向制导律的思想设计圆弧段路径的LOS航向制导律。假设欲跟随的路径为圆po,路径方向 为顺时针;pk为UUV所在点Pt与圆心po连线和圆po的交点,该点的切线为l;
为顺时针;pk为UUV所在点Pt与圆心po连线和圆po的交点,该点的切线为l; 为点Pk处切线上的前视点,与点pk的距离
为点Pk处切线上的前视点,与点pk的距离 ,该前视点的方向由跟随路径方向
,该前视点的方向由跟随路径方向 唯一确定;固定坐标系北向与
唯一确定;固定坐标系北向与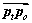 的夹角定义为
的夹角定义为 ;
;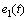 为横向跟随误差。圆弧段路径中各个变量的几何关系如图3所示。
为横向跟随误差。圆弧段路径中各个变量的几何关系如图3所示。
根据图3可知:圆弧段路径的LOS航向制导律为:
 (8)
(8)
该制导律在形式上与直线段路径的LOS航向制导律完全一致。
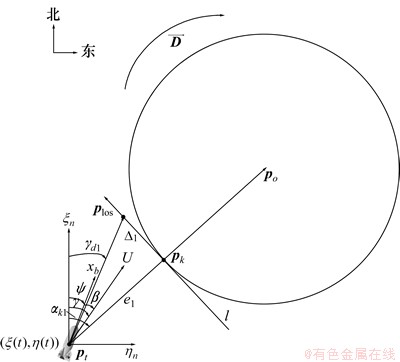
图3 圆弧段路径的LOS航向制导律的原理图
Fig.3 Principle of LOS guidance for circular arcs in horizontal plane
3 自适应神经网络路径跟随控制器设计
本节的控制目标为:设计自适应神经网络控制器,使得航向跟踪误差方程中的: ,进而横向跟随误差
,进而横向跟随误差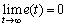 ,最终实现欠驱动UUV在水平面的路径跟随控制。
,最终实现欠驱动UUV在水平面的路径跟随控制。
为方便控制器设计,定义
 ,
, 
由UUV水平面机动模型知,欲控制UUV航向需引入航向运动差分方程,将水平面路径跟随控制的运动方程改写为
 (9)
(9)
其中: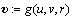 ,包括艏向运动方程中的非线性项;d为干扰,包括未建模误差和外部扰动,满足
,包括艏向运动方程中的非线性项;d为干扰,包括未建模误差和外部扰动,满足  ,
, 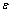 >0。
>0。
定义航向跟踪误差:
 . (10)
. (10)
取 ,使得式(9)描述的系统稳定。
,使得式(9)描述的系统稳定。
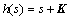 (11)
(11)
那么,航向跟踪误差的微分形式可表示为
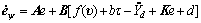 (12)
(12)
其中: ,B=1。可找到P>0,Q≥0使得
,B=1。可找到P>0,Q≥0使得
 (13)
(13)
如果 和b均已知,并且系统干扰d=0,那么利用极点配置方法可得如下的线性运动控制器:
和b均已知,并且系统干扰d=0,那么利用极点配置方法可得如下的线性运动控制器:
 (14)
(14)
结合航向控制运动方程,可知
 (15)
(15)
由于K 保证式(9)描述的系统稳定,因此,

实际中, 和b有可能未知,同时系统干扰d也存在。为了解决非线性不确定项以及未知扰动给控制器设计带来的困难, 设计一个径向基神经网络(RBF NN) 估计
和b有可能未知,同时系统干扰d也存在。为了解决非线性不确定项以及未知扰动给控制器设计带来的困难, 设计一个径向基神经网络(RBF NN) 估计 及d:
及d:
 (16)
(16)
其中: 为
为 的估计值;
的估计值; 为高斯函数,
为高斯函数,
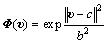
 为高斯函数的中心;b为该高斯函数的宽度。当
为高斯函数的中心;b为该高斯函数的宽度。当  一致有界时,可以找到1个正小量使得:
一致有界时,可以找到1个正小量使得: 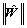 <w。
<w。
由于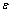 是RBF NN的估计误差,故
是RBF NN的估计误差,故
 (17)
(17)
同时,定义该RBF NN的权值误差为
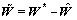 (18)
(18)
结合公式(12)知:
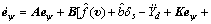
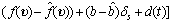


 (19)
(19)
在式(19)中,为补偿神经网络的估计误差及系统干扰项引起的控制偏差,设计1个虚拟控制量
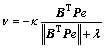 (20)
(20)
其中: ,
, ;
; 为一正常量。
为一正常量。
因此,式(19)可改写为
 (21)
(21)
引入自适应律:
 (22)
(22)
为保证设计的自适应神经网络控制器给出的控制量可使与路径跟随相关的状态均有界,选择1个Lyapunov函数:
 (23)
(23)
式(23)的微分形式为
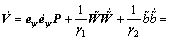
 (24)
(24)
将式(21)代入式(24)得
 (25)
(25)
因为



且 成立,由式(25)可得:
成立,由式(25)可得:
 (26)
(26)
已知 ,故
,故
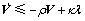 (27)
(27)
其中: >0。
>0。
基于Lyapunov稳定性理论可知:该路径跟随控制系统的状态都是一致最终有界的,通过合适的选择控制参数可以使得航向控制误差渐近收敛至零。
最终可得自适应神经网络路径跟随控制器的具体表达式:
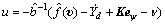 (28)
(28)
4 仿真结果与分析
仿真研究对象为哈尔滨工程大学北飒海洋装置与控制技研究所自主研发的UUV,利用其缩尺度模型测得的水动力系数构建非线性模型,并基于该运动模型对上述研究的水平面路径跟随控制器的正确性和有效性进行验证。其水平面运动模型的无因次水动力系数 ,
,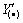 和
和 的数值如表1所示。
的数值如表1所示。
在相同的初始条件,相同的控制目标下进行水平面路径跟随试验,2种路径方案包括:直线段跟随路径和圆弧连接的直线段跟随路径。结合直线段LOS航向制导律和圆弧路径的圆弧LOS航向制导律,利用自适应神经网络控制器进行水平面路径跟随控制对比试验,初始值设定如下。
潜器初始位置: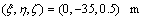 ;
;
初始姿态角: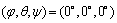 ;
;
指令速度:ud=1.8 m/s。
另外,自适应神经网络控制器的增益及控制参数设定为K=2.8,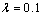 ,
, 和
和 ,RBF神经网络的中心值为2,宽度为5,网络初始权值取为0。
,RBF神经网络的中心值为2,宽度为5,网络初始权值取为0。
表1 UUV水平面无因次水动力系数
Table 1 UUV’s non-dimensional hydrodynamic coefficients

环境中存在时不变海流,海流方向朝西,速度约为0.25 m/s。为尽可能接近实际情况,在直线段跟随路径中路径为4个直线段顺序连接,其中包括3种转角:直角,钝角和锐角,分别为90°,135°和45°。2种路径方案下,仿真结果如图4~8所示。
图4和图5所示为2种路径下UUV在北东坐标系下的位置变化曲线,在速度为0.25 m/s,方向为由东向西的海流干扰下,显然两者的最大不同在航行段的交界处。在相同的初始条件,相同的控制目标下进行水平面路径跟随试验,由圆弧连接的直线段路径跟随方案,当航行段通过圆弧连接后,相比由直线段连接的直线段路径跟随方案,在转角处的位置跟随误差大大减小。

图4 ANNC下直线段跟随路径曲线
Fig. 4 Path following of straight-lines with adaptive NN controller
图6(a)和(b)分别为圆弧连接的直线段跟随路径时的纵向运动速度曲线和横向运动速度曲线。由图6(a)可知:载体纵向运动航速可控,且航行速度在直线段航行过程中一直稳定地保持在设定航速,仅在转弯处有小幅度变化,这可消除减速转弯对航行深度带来的影响。根据图7可知:当通过圆弧连接相邻的航行段后,跟随路径的航向随位置连续变化不再引起跳跃变化,则航向制导律得到的航向指令不会产生大幅度跳跃,此时在转角处的位置误差自然可减小。

图5 ANNC下圆弧连接的直线段跟随路径曲线
Fig. 5 Path following of straight-lines and arcs with adaptive NN controller

图6 圆弧连接的直线段跟随路径时的速度曲线
Fig. 6 Speed response of straight-lines and arcs with adaptive NN controller

图7 2种路径方案下航行制导律的变化曲线
Fig. 7 Response of heading guidance under the two path profiles
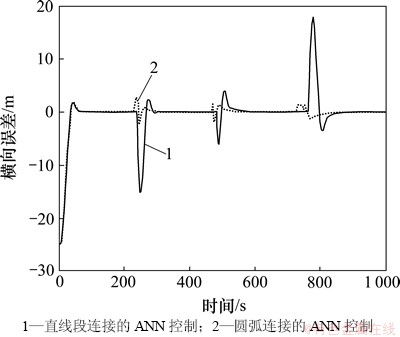
图8 2种路径方案下横向误差曲线
Fig. 8 Cross-track errors of the two path profiles
5 结论
1) 针对UUV水动力参数变化和不确定项干扰下的精确水平面路径跟随问题,基于李雅普诺夫稳定性理论设计了自适应神经网络控制器,可保证水平面路径跟随控制系统中所有的误差状态渐近稳定。
2) 在每个拐点处设计合适半径的弧线连接两个路径部分,使得水平面机动时拐角处的跟随误差限制在设计范围内。
3) 仿真实验表明该方法是有效的,与单独直线段路径跟随控制相比,改进规则下自适应神经网络的路径跟随控制器可使得拐点处的跟踪误差较大幅度减小,具有较好的工程使用价值。
参考文献:
[1] 贾鹤鸣, 张利军, 边信黔, 等. 基于非线性迭代滑模的欠驱动UUV三维航迹跟踪控制[J]. 自动化学报, 2012, 38(2): 308-314.
JIA Heming, ZHANG Lijun, BIAN Xinqian, et al. Three dimensional path following control for an underactuated UUV based on nonlinear iterative sliding mode[J]. Acta Automatica Sinica, 2012, 38(2): 308-314.
[2] Wang B, Su Y M, Wan L, et al. Adaptive PID control system for an autonomous underwater vehicle[J]. High Technology Letters, 2011, 17(1): 7-12.
[3] Li J H, Lee P M. Path tracking in dive plane for a class of torpedotype underactuated AUVs[C]// Proceedings of the 7th Asian Control Conference. Piscataway, NJ, USA: IEEE, 2009, 8: 360-365.
[4] 张利军, 贾鹤鸣, 边信黔, 等. 基于L2干扰抑制的水下机器人三维航迹跟踪控制[J]. 控制理论与应用, 2011, 28(5): 645-651.
ZHANG Lijun, JIA Heming, BIAN Xinqian, et al. Three-dimensional path tracking control for an autonomous underwater vehicle based on L-two disturbance attenuation method[J]. Control Theory & Applications, 2011, 28(5): 645-651.
[5] 唐旭东, 庞永杰, 李晔, 等. 基于混沌过程神经元的水下机器人运动控制方法[J]. 控制与决策, 2010, 25(2): 213-217.
TANG Xudong, PANG Yongjie, LI Ye, et al. Chaotic process neuron control for AUVs[J]. Control and Decision, 2010, 25(2): 213-217.
[6] 边信黔, 程相勤, 贾鹤鸣, 等. 基于迭代滑模增量反馈的欠驱动AUV的地形跟踪控制[J]. 控制与决策, 2011, 26(2): 289-292.
BIAN Xinqian, CHENG Xiangqin, JIA Heming, et al. A bottom-following controller for underactuated AUV based on iterative sliding and increment feedback[J]. Control and Decision, 2011, 26(2): 289-292.
[7] 毕凤阳, 张嘉钟, 魏英杰, 等. 模型不确定时滞欠驱动AUV的模糊变结构控制[J]. 哈尔滨工业大学学报, 2010, 42(3): 358-363.
BI Fengyang, ZHANG Jiazhong, WEI Yingjie, et al. A fuzzy sliding mode controller for underactuated autonomous underwater vehicles with uncertain time delay[J]. Journal of Harbin Institute of Technology, 2010, 42(3): 358-363.
[8] 施淑伟, 严卫生, 高剑, 等. 常值海流作用下的AUV水平面路径跟踪控制[J]. 兵工学报, 2010, 31(3): 375-379.
SHI Shuwei, YAN Weisheng, GAO Jian, et al. Path following control of an AUV in the horizontal plane with constant ocean currents[J]. Acta Armamentar II, 2010, 31(3): 375-379.
[9] Fossen T I. Handbook of marine craft hydrodynamics and motion control[M]. Norway: A John Wiley & Sons, Ltd., 2011: 243-246.
[10] Oh S R, SUN Jing. Path following of underactuated marine surface vessels using line-of-sight based model predictive control[J]. Ocean Engineering, 2010, 37: 289-295.
[11]  E, Pavlov A, Pettersen K Y. Integral LOS control for path following of underactuated marine surface vessels in the presence of constant ocean currents[C]// Proceedings of the 47th IEEE Conference on Decision and Control. Cancun, Mexico, 2008: 4984-4991.
E, Pavlov A, Pettersen K Y. Integral LOS control for path following of underactuated marine surface vessels in the presence of constant ocean currents[C]// Proceedings of the 47th IEEE Conference on Decision and Control. Cancun, Mexico, 2008: 4984-4991.
[12] BIAN Xinqian, ZHOU Jiajia, JIA Heming, et al. Adaptive neural network control system of bottom following for an underactuated AUV[C]// OCEANS'10 MTS/IEEE. Seattle, 2010: 1-6.
[13] 贾鹤鸣, 张利军, 齐雪, 等. 基于神经网络的水下机器人三维航迹跟踪控制[J]. 控制理论与应用, 2012, 29(7): 877-883.
JIA Heming, ZHANG Lijun, QI Xue, et al. Three-dimensional path tracking control for autonomous underwater vehicle based on neural network[J]. Control Theory & Applications, 2012, 29(7): 877-883.
[14] Antonelli G. On the use of adaptive/integral actions for six-degrees-of-freedom control of autonomous underwater vehicles[J]. Ocean Engineering, 2007, 32(2): 300-312.
[15] 于金霞, 蔡自兴, 邹小兵, 等. 基于神经网络辨识的移动机器人航向误差校准方法[J]. 中南大学学报(自然科学版), 2005, 36(5): 745-750.
YU Jinxia, CAI Zixing, ZOU Xiaobing, et al. Calibration method for heading error of mobile robot based on neural networks identification[J]. Journal of Central South University (Science and Technology), 2005, 36(5): 745-750.
(编辑 何运斌)
收稿日期:2013-09-03;修回日期:2013-11-22
基金项目:国家自然科学基金资助项目(51179038,51109043);教育部新世纪优秀人才支持计划项目(NCET-10-0053);中央高校基本科研业务资助项目(HEUCF1421002)
通信作者:周佳加(1982-),男,浙江杭州人,博士,讲师,从事水下机器人控制技术研究;电话:0451-82519306;E-mail: choujaa123@163.com