Barton-Bandis criterion-based system reliability analysis of rock slopes
来源期刊:中南大学学报(英文版)2020年第7期
论文作者:赵炼恒 左仕 胡昌文 张迎宾 宋祉辰
文章页码:2123 - 2133
Key words:Barton-Bandis criterion; failure mode; probability of failure; rock slope; system reliability analysis
Abstract: Several potential failure modes generally exist in rock slopes because of the existence of massive structural planes in rock masses. A system reliability analyses method for rock slopes with multiple failure modes based on nonlinear Barton-Bandis failure criterion is proposed. The factors of safety associated with the sliding and overturning failure modes are derived, respectively. The validity of this method is verified through a planar rock slope with an inclined slope top and tension crack. Several sensitivity analyses are adopted to study the influences of structural-plane parameters, geometric parameters, anchoring parameters and fracture morphology on the rock slopes system reliability.
Cite this article as: ZUO Shi, HU Chang-wen, ZHAO Lian-heng, ZHANG Ying-bin, SONG Zhi-chen. Barton-Bandis criterion-based system reliability analysis of rock slopes [J]. Journal of Central South University, 2020, 27(7): 2123-2133. DOI: https://doi.org/10.1007/s11771-020-4435-6.

J. Cent. South Univ. (2020) 27: 2123-2133
DOI: https://doi.org/10.1007/s11771-020-4435-6

ZUO Shi(左仕)1, HU Chang-wen(胡昌文)2, ZHAO Lian-heng(赵炼恒)1, 3,ZHANG Ying-bin(张迎宾)4, SONG Zhi-chen(宋祉辰)1
1. School of Civil Engineering, Central South University, Changsha 410075, China;
2. Shenzhen Transportation Design & Research Institute, Shenzhen 518003, China;
3. Key Laboratory of Heavy-haul Railway Engineering Structure of Ministry of Education,Central South University, Changsha 410075, China;
4. Department of Civil and Structure Engineering, Kyushu University, Fukuoka 8190395, Japan
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: Several potential failure modes generally exist in rock slopes because of the existence of massive structural planes in rock masses. A system reliability analyses method for rock slopes with multiple failure modes based on nonlinear Barton-Bandis failure criterion is proposed. The factors of safety associated with the sliding and overturning failure modes are derived, respectively. The validity of this method is verified through a planar rock slope with an inclined slope top and tension crack. Several sensitivity analyses are adopted to study the influences of structural-plane parameters, geometric parameters, anchoring parameters and fracture morphology on the rock slopes system reliability.
Key words: Barton-Bandis criterion; failure mode; probability of failure; rock slope; system reliability analysis
Cite this article as: ZUO Shi, HU Chang-wen, ZHAO Lian-heng, ZHANG Ying-bin, SONG Zhi-chen. Barton-Bandis criterion-based system reliability analysis of rock slopes [J]. Journal of Central South University, 2020, 27(7): 2123-2133. DOI: https://doi.org/10.1007/s11771-020-4435-6.
1 Introduction
The safety assessment of rock slopes is a significant research topic in geotechnical engineering [1-9]. Conventional deterministic analysis methods cannot effectively account for the influences of various uncertainties and multiple potential failure modes that arise from the complexity of the rock mass forming process [4, 10-16]. Thus, it is of great necessity to adopt a system reliability analysis method to evaluate the reliability of rock slope with several potential failure modes. For example, JIMENEZ- RODRIGUEZ et al [17, 18] analyzed the system reliability of planar- and wedge-shaped rock slope with potential failure modes using the Monte Carlo simulation. LI et al [13] and LOW [19] both analyzed the stability of rock slopes with different failure modes by adopting the system reliability method. LI et al [20] analyzed the system reliability of anchor-stabilised slopes. JIANG et al [21] proposed an efficient subset simulation-based approach for rock slopes system reliability analysis. OBREGON et al [15] used a probabilistic-based approach to analyze slope stability.
It can be found that the aforementioned studies are based on the Mohr-Coulomb (M-C) failure criterion. Research has demonstrated that this criterion cannot accurately reflect the intensity characteristics of rock sliding along structural planes, especially under a relatively small normal stress [22-24]. Alternative criterions are advocated to predict the shear strength of the rock joint. The Barton-Bandis (B-B) failure criterion developed by BARTON and BANDIS [25-27] is preferable for such purpose. Recently, the B-B failure model and its variants [28-31] have been widely applied to stability analyses of rock slopes. For instance, CHOI and CHUNG [1] conducted numerical simulations using Universal Distinct Element Code (UDEC) and confirmed the B-B failure model could accurately reflect the actual failure processes of rock slopes. KVELDSVIK et al [32] investigated the effects of the B-B criterion on the Aknes rock slope stability, Norway. Furthermore, the B-B failure criterion has been adopted in the rock slope reliability analysis. FENG and LAJTAI [11] conducted a probabilistic analysis of the sliding wedge using the non-linear B-B failure criterion. DUZGUN et al [33] performed slope probabilistic stability analysis with considering uncertainties of the B-B criterion parameters. ZHAO et al [34-36] adopted the reliability analysis method and system reliability analysis method to study the stability of rock slopes based on the B-B failure criterion successively. However, only the failure mode of a single wedge-shaped rock was considered. Few studies were made to investigate the B-B failure criterion-based reliability of rock slopes incorporating several potential failure modes.
Based on ZHAO et al [34], a nonlinear B-B failure criterion-based system reliability analysis method is proposed for rock slopes with several failure modes. The factors of safety (FS) associated with the sliding and overturning failure modes for rock slopes are derived. By taking a rock slope with an inclined slope top and tension crack as an analysis case, the validity of this method is verified. The influences of structural-plane parameters, geometric parameters, anchoring parameters and fracture morphology on the slope system reliability are investigated through a series of sensitivity analyses.
2 Stability analyses of rock slopes
2.1 Nonlinear Barton-Bandis failure criterion
Due to the wide distribution of the joint plane, the relationship between shear strength and normal stress for rock slopes is nonlinear. To describe this characteristic accurately, Barton and Bandis proposed a model to predict the strength of rock mass well, and the estimation method of key parameters of this model is becoming more and more mature. So the B-B model has been widely adopted, which is expressed as [25, 27]:
 (1)
(1)
where τ and σn are the shear and normal stress of the structural plane respectively; JRC, JCS and φb are the coefficient of joint roughness, the effective compressive strength and the basic friction angle of the structural plane, respectively. The values of JRC, JCS and φb are commonly determined from field experiments [22, 23, 37]. And this criterion applies to 0.01<σn/σc<0.3, in which σc is rock uniaxial compressive strength. The stress levels underlying the rock slope stability problems are almost within this range. As indicated by HOEK and BRAY [2], the Barton formula in Eq. (1) can accurately predict the shear strength of structural planes in rock slope engineering only when the maximum value of the expression in the bracket in Eq. (1) is less than 70°.
2.2 Failure modes
Several potential failure modes generally exist in rock slope due to the existence of massive structural planes. And anchors are often used for slope reinforcement [38, 39]. Based on the model of ZHAO et al [34], the planar rock slope model with considering the tension crack and anchoring effect is adopted in this study. Figure 1 illustrates the geometric characteristics of the model, which two blocks separated by an inclined crack. H is the slope height; β is the slope dip; θ is the sliding surface dip; α is the upper slope surface dip; XL is the distance from the top of crack to the slope toe; ζL is the coefficient of crack displacement,  δ is the dip of tension crack; XM is the horizontal distance from the action point of the anchoring force to the slope toe; ζM is the coefficient of anchor position,
δ is the dip of tension crack; XM is the horizontal distance from the action point of the anchoring force to the slope toe; ζM is the coefficient of anchor position,  Depending on the crack’s location and the stability of block B, there are four possible sliding failure modes. When the crack locates at the slope top: failure mode 1 refers to the absence of the interaction among blocks, and failure mode 2 refers to the existence of interaction between blocks; When the crack locates at the slope face: failure mode 3 refers to the absence of interaction among blocks, and mode 4 refers to the existence of interaction among blocks.
Depending on the crack’s location and the stability of block B, there are four possible sliding failure modes. When the crack locates at the slope top: failure mode 1 refers to the absence of the interaction among blocks, and failure mode 2 refers to the existence of interaction between blocks; When the crack locates at the slope face: failure mode 3 refers to the absence of interaction among blocks, and mode 4 refers to the existence of interaction among blocks.
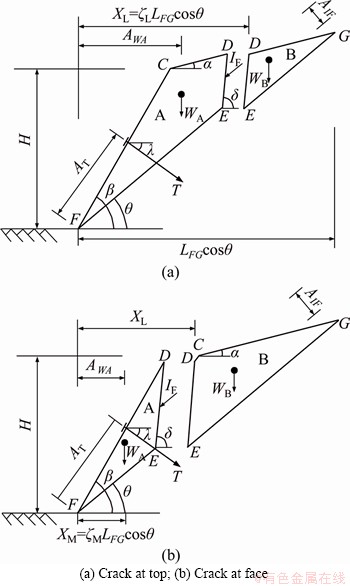
Figure 1 Planar rock slope model for stability analyses:
2.3 Stability analysis
For the model in Figure 1, the FS associated with the sliding failure modes can be calculated as the ratio of the total sliding resistance to the total sliding force [2, 40-42]. The state of block B shall be determined before performing slope stability analysis because it can significantly affect the potential failure modes. Two cases are considered: 1) Block B is stable and no interactions among blocks; 2) Block B is unstable and exerts a residual downward sliding-force (IF) on block A. Note that, the fracture position is taken as a random variable, which could lead to the anchoring force exerted on either Block A or B. Hence, in the stability analysis, anchoring force should be considered in the FS deduction of blocks A and B and the programming computation should be carried out based on the relative crack-anchor positions.
Case 1: Block B is stable.
When block B is stable, no interactions exist between these two blocks. Block A does not experience overturning failure under the gravity and anchoring force. The normal stress of block A on the sliding surface can be estimated as
 (2)
(2)
where WA is the gravity of sliding block A; θ is the sliding surface dip; λ is the setting angle of the anchor; T is the anchoring force of the anchor steel; LEF is the length of failure plane of block A.
Based on the B-B model, the total sliding resistance of block A can be calculated as
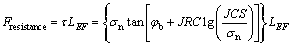
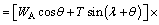
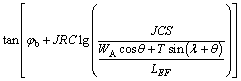 (3)
(3)
The total sliding force of block A can be calculated as
 (4)
(4)
Then, the FS of block A can be derived as
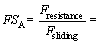

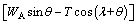 (5)
(5)
Similarly, the FS of block B can be derived as


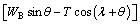 (6)
(6)
where WB is the gravity of sliding block B. The details for calculation of the geometric parameters and force arms of the two blocks can be found in Appendix A.
Case 2: Block B is unstable.
Once block B undergoes sliding failure, it will exert a residual downward sliding-force, IF, on block A, which will affect the stability of block A. In this case, it can be assumed that there exists an interaction force between the two blocks. The interaction force (IF) can be calculated by making FSB=1.0 [13, 18, 34, 43]:
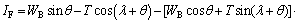
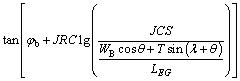 (7)
(7)
When IF is computed, the sliding FS of block A can be also determined through limit equilibrium analysis:
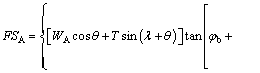

 (8)
(8)
Besides, block A has the potential to experience overturning failure around the slope toe under the gravity, anchoring force and sliding force IF. The resisting overturning FS of block A can be estimated as
 (9)
(9)
where AT, AWA and AIF are the force arms of T, WA and IF, respectively, when block A rotates around the slope toe (i.e., point F in Figure 1). Block A is unlikely to undergo the overturning failure when FSA-F >1.
3 System reliability analysis of rock slope
As discussed in Section 2.2, the considered rock slope has four potential failure modes. Anyone of such scenarios is an indicator of the failure of the overall rock slope. Therefore, it can be regarded as a series system comprising four subsystems satisfying their respective limit state conditions. Figure 2 shows the system configuration of the slope and corresponding limit state functions. In Figure 2, the slope system is considered as a series system consisting of four subsystems 1, 2, 3 and 4, each of which is independent and represents a failure mode. Each subsystem contains three different components. Table 1 shows the meaning of the component limit state functions g1-g9. Then, the system failure probability is calculated by using Monte-Carlo simulation (MCS). This is because the MCS is conceptually simple and easily implementable, and the results are relatively accurate as long as the sample size is large enough to ensure the coefficient of variation of failure probability smaller than 10% [13, 21].
4 Numerical examples
4.1 Determination of input parameters
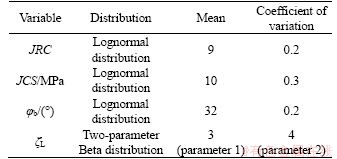
To illustrate the proposed approach, the rock slope as shown in Figure 1 is adopted as an example. The structural-plane parameters JRC, JCS and φb are regarded as log-normally distributed random variables, while ζL is assumed to follow two-parameter beta distribution (Table 2) [11, 31]. Other parameters are set to be deterministic as follows: β=64°, δ=80°, θ=35°, λ=30°, α=15°, γ=27 kN/m3, ζM=0.1, H=60 m and T=500 kN.

Figure 2 System configuration of rock slope
Table 1 Interpretation of component limit state functions
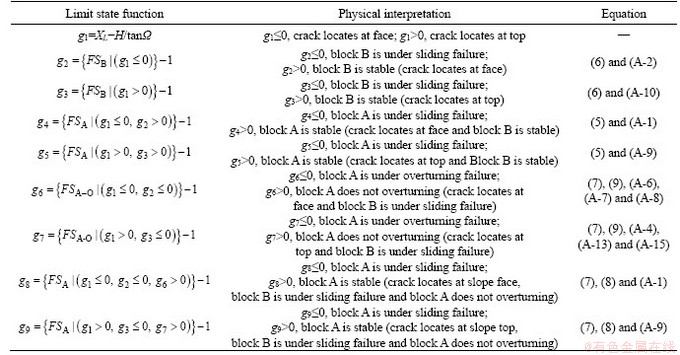
Table 2 Statistical properties of variables
4.2 Effects of structural-plane parameters on system reliability
To analyze the effects of structural-plane parameters on the system reliability, the means of JRC, JCS and φb vary in the ranges of [4, 16],[10 MPa, 100 MPa], and [26°, 44°], respectively. The Monte-Carlo simulation with N=1×106 sets of random samples is utilized to compute the failure probabilities for each failure mode and slope system. Figures 3(a)-(c) present the change of the failure probability with the means of JRC, JCS and φb, respectively. As shown in Figure 3, Pf,1 (the failure probability for the failure mode 1) almost approaches zero, indicating that the rock slope will keep stable if the crack locates at the slope face and block B is also stable. The failure mode 4 is the most likely to occur because Pf,4 is the maximum among these modes. Pf,sys (the failure probability of the slope system) relies greatly on Pf,4. Additionally, Pf,sys decreases pronouncedly with increasing the means of φb, JRC, and JCS. This result implies that the stability of the slope can be enhanced evidently as the basic friction angle, roughness coefficient or effective compressive strength of the structural plane increase.
4.3 Effects of anchoring parameters on system reliability
To analyze the effects of anchoring parameters on the system reliability, the mean of ζL is set as 0.2, 0.4, 0.6 and 0.8, respectively. The anchoring angle λ and anchoring force T vary in the ranges of [-50°, 80°] and [0, 500 kN], respectively. In addition, to reflect the influence of anchoring effect on different blocks, ζM=0.1 and 0.9 are selected for illustration. Figures 4(a) and (b) present the failure probabilities of the slope system underlying ζM=0.1 and ζM=0.9 for various anchoring angles λ. Figures 4(c) and (d) present the failure probabilities of the slope system underlying ζM=0.1 and ζM=0.9 for various anchoring forces T.
It can be observed from Figure 4 that both the anchoring angle and anchoring force substantially influence the Pf,sys. The Pf,sys decreases with an increasing anchoring force, while it initially decreases and then increases as the anchoring angle varies from an upswept direction to a downward direction. It indicates that higher slope stability can be achieved at a lower anchoring angle and a larger anchoring force. It is also interesting to observe that the Pf,sys is affected by neither the anchoring angle nor the anchoring force in some situations (see Figures 4(b) and (d)). This is due to the fact that the block B in these situations can be stable by itself without the reinforcements of anchors. Moreover, when different anchoring locations on blocks A or B are used, the reinforcement effects of anchors on the slope system could be different although the anchoring angle and anchoring force are the same. Therefore, to enhance the reinforcement effects of anchors, the various anchoring factors including anchoring angle, anchoring force and anchoring location should be comprehensively accounted for in practice.

Figure 3 Effects of structural-plane parameters:
4.4 Effect of fracture morphology on system reliability
As discussed previously, the overturning failure of block A may occur when block B loses its stability. To illustrate the effect of fracture morphology on the failure modes, the discrete element software “UDEC” is adopted to simulate the failure patterns of the slope since it can well simulate the large deformation of the structural plane [1, 44, 45]. Two discrete element models consisting of 8758 and 8696 triangle elements are established in UDEC based on the B-B failure criterion with two cases: (a) ζL=0.2, δ=100° and (b) ζL=0.4, δ=100°, respectively. Figure 5 presents the velocity vectors and deformed meshes of the rock slope. It is evident that the rock slope can experience overturning failure as well as the sliding failure as the fracture morphology changes. For the case (a), block A experiences overturning failure with its velocity vectors pointing toward the slope free face rather than along the direction of failure plane. For the case (b), block A experiences sliding failure with its velocity vectors pointing down along the direction of failure plane. These phenomena confirm that the rock slope reliability analysis only considering the sliding failure mode may lead to inaccurate results [33-36].
To further investigate the effects of the fracture morphology, δ is set as 70°, 80°, 90° and 100°, respectively. Figure 6 presents the probability of overturning failure with the mean of ζL varying from 0.1 to 0.9. For the case of a relatively small mean of ζL, a high probability of overturning failure can be obtained, indicating the stability of the slope system is dominated by the overturning failure. The instability of the slope system is gradually manifested as the sliding failure as the mean of ζL increases (see the red dots in Figure 6 which shows extremely low probability of overturning failure). Additionally, the Pf,sys varies notably when the location of the crack changes from the slope face to the slope top. The results show that the slope stability is also sensitive to the fracture morphology.
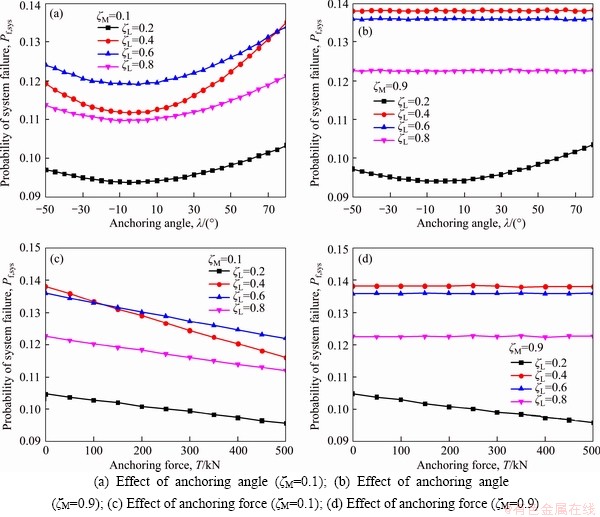
Figure 4 Effects of anchoring parameters:

Figure 5 Effect of fracture morphology on failure modes of rock slope:
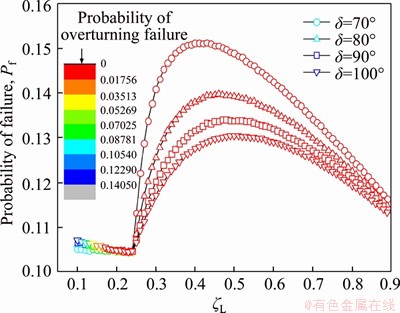
Figure 6 Effect of fracture morphology
4.5 Effect of geometric parameters on system reliability
Apart from the strength parameters of the joints, the geometric parameters of the slope also affect the stability of rock slopes. So the effects of the geometric parameters are investigated here. To analyze the influence of the four parameters that control the shape of the slope body, the anchoring effect is not considered, the fracture morphology is fixed (δ=80°, ζL=0.4) and the structural-plane parameters are regarded as fixed values. To control the rationality of slope shape, it is assumed that each parameter is subject to the truncated normal distribution, and the upper and lower limits are the μ±2σ (Table 3).
Computational analysis was implemented by changing one variable each time for obtaining the failure probability of each sub-system and the Pf,sys (Figure 7).
It can be seen from Figure 7 that only when θ increases, there are three different failure modes within this parameter range. When the other three parameters change, only the failure mode 3 occurs.
Table 3 Statistical properties of geometric parameters


Figure 7 Effects of geometric parameters:
And the failure mode 1 does not occur when four parameters change. In addition, with the increase of each parameter, the Pf,sys increases, indicating that the slope becomes more unstable.
5 Conclusions
A system reliability analyses method for rock slopes with several potential failure modes is proposed based on Barton-Bandis failure criterion. A rock slope with two sliding blocks is adopted as an example. A series of sensitivity analyses are carried out for the influences of structural-plane parameters, anchoring parameters and fracture morphology on the system reliability.
1) The structural-plane parameters JRC, JCS and φb, can substantially affect the stability of rock slopes. The stability can be greatly enhanced with increasing the values of JRC, JCS or φb. While with the increase of geometric parameters values, the slope becomes more unstable.
2) For the considered rock slope, Pf,sys decreases as the anchoring force increases, while it initially decreases and then increases as the anchoring angle gradually varies from an upswept direction to a downward direction. Various anchoring schemes which can affect the reinforcement effects of anchors on the slope system should be comprehensively accounted for in practice.
3) Both the sliding failure mode and overturning failure mode should be properly considered. Depending on the fracture morphology, the stability of the slope system can be dominated by sliding failure or overturning failure. The slope stability is sensitive to the fracture morphology.
4) The proposed approach is validated through stability analysis of a simple rock slope with an inclined slope top and tension crack. However, further efforts are needed on the system reliability evaluations of complex three-dimensional rock slopes, which can more realistically simulate the real situation in engineering practice.
Appendix A
The geometric parameters and force arms of blocks A and B as shown in Figure 1 are calculated based on the following methods:
1) Tension crack at the slope face (0<XL<H/tanβ)
 (A-1)
(A-1)
 (A-2)
(A-2)
 (A-3)
(A-3)
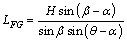 (A-4)
(A-4)
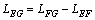 (A-5)
(A-5)
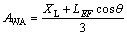 (A-6)
(A-6)
 (A-7)
(A-7)
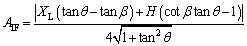 (A-8)
(A-8)
where IF is the residual down sliding force of block B after failure; and AT, AWA and AIF are the force arms of T, WA and IF, respectively, when block A rotates around the slope toe (i.e., point F in Figure 1); γ is the unit weight (kN/m3).
2) Tension crack at the slope top 
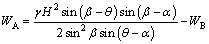 (A-9)
(A-9)
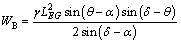 (A-10)
(A-10)
 (A-11)
(A-11)
 (A-12)
(A-12)
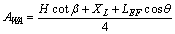 (A-13)
(A-13)
 (A-14)
(A-14)
 (A-15)
(A-15)
References
[1] CHOI S O, CHUNG S. Stability analysis of jointed rock slopes with the Barton-Bandis constitutive model in udec [J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(3): 581-586. DOI: 10.1016/ j.ijrmms.2003.12.142.
[2] HOEK E, BRAY J W. Rock slope engineering [M]. 3rd ed. London: Institution of Mining and Metallurgy, 1981.
[3] JIANG Qing-hui, QI Zu-fang, WEI Wei, ZHOU Chuang-bing. Stability assessment of a high rock slope by strength reduction finite element method [J]. Bulletin of Engineering Geology and the Environment, 2015, 74(4): 1153-1162. DOI: 10.1007/s10064-014-0698-1.
[4] LI Bo, ZHOU Kai-feng, YE Jun, SHA Peng. Application of a probabilistic method based on neutrosophic number in rock slope stability assessment [J]. Applied Sciences, 2019, 9(11): 2309. DOI: 10.3390/app9112309.
[5] LI Xue-you, FAN Zeng-bin, LU Tao, XIAO Te, ZHANG Li-ming. A resilience model for engineered slopes subject to anchor corrosion [J]. KSCE Journal of Civil Engineering, 2018, 22(3): 887-895. DOI: 10.1007/s12205-018-1041-3.
[6] ZHAO Lian-heng, ZHANG Shuai-hao, HUANG Dong- liang, ZUO Shi, LI De-jian. Quantitative characterization of joint roughness based on semivariogram parameters [J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 109: 1-8. DOI: 10.1016/j.ijrmms.2018. 06.008.
[7] SARI M. Stability analysis of cut slopes using empirical, kinematical, numerical and limit equilibrium methods: Case of old Jeddah–Mecca road (Saudi Arabia) [J]. Environmental Earth Sciences, 2019, 78(21): 621. DOI: 10.1007/s12665- 019-8573-9.
[8] DENG Dong-ping, ZHAO Lian-heng, LI Liang. Limit equilibrium analysis for rock slope stability using basic Hoek–Brown strength criterion [J]. Journal of Central South University, 2017, 24(9): 2154-2163. DOI: 10.1007/s11771- 017-3624-4.
[9] LI Xiong-wei, ZHU Jian-qun, LI Zheng-wei, YANG Xiao-li. 3D stability assessment of stepped slopes in inhomogeneous soils [J]. Journal of Central South University, 2020, 27(1): 221-230. DOI: 10.1007/s11771-020-4290-5.
[10] CHENG Yan-hui, HE Dong-liang. Slope reliability analysis considering variability of shear strength parameters [J]. Geotechnical and Geological Engineering, 2020: 1-8. DOI: 10.1007/s10706-020-01266-w.
[11] FENG Ping, LAJTAI E Z. Probabilistic treatment of the sliding wedge with EzSlide [J]. Engineering Geology, 1998, 50(1): 153-163. DOI: 10.1016/s0013-7952(98)00007-6.
[12] GRAVANIS E, PANTELIDIS L, GRIFFITHS D V. An analytical solution in probabilistic rock slope stability assessment based on random fields [J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 71: 19-24. DOI: 10.1016/j.ijrmms.2014.06.018.
[13] LI Dian-qing, JIANG Shui-hua, CHEN Yi-feng, ZHOU Chuang-bin. System reliability analysis of rock slope stability involving correlated failure modes [J]. KSCE Journal of Civil Engineering, 2011, 15(8): 1349-1359. DOI: 10.1007/s12205-011-1250-5.
[14] LI Dian-qing, ZHOU Chuang-bin, LU Wen-bo, JIANG Qing-hui. A system reliability approach for evaluating stability of rock wedges with correlated failure modes [J]. Computers and Geotechnics, 2009, 36(8): 1298-1307. DOI: 10.1016/j.compgeo.2009.05.013.
[15] OBREGON C, MITRI H S. Probabilistic approach for open pit bench slope stability analysis–A mine case study [J]. International Journal of Mining Science and Technology, 2019, 29(4): 629-640. DOI: 10.1016/j.ijmst.2019.06.017.
[16] PENG Xing, LI Dian-qing, CAO Zi-jun, GONG Wei-ping, JUANG C H. Reliability-based robust geotechnical design using Monte Carlo simulation [J]. Bulletin of Engineering Geology and the Environment, 2017, 76(3): 1-11. DOI: 10.1007/s10064-016-0905-3.
[17] JIMENEZRODRIGUEZ R, SITAR N. Rock wedge stability analysis using system reliability methods [J]. Rock Mechanics and Rock Engineering, 2007, 40(4): 419-427. DOI: 10.1007/s00603-005-0088-x.
[18] JIMENEZRODRIGUEZ R, SITAR N, CHACON J. System reliability approach to rock slope stability [J]. International Journal of Rock Mechanics and Mining Sciences, 2006, 43(6): 847-859. DOI: 10.1016/j.ijrmms.2005.11.011.
[19] LOW B K. Reliability analysis of rock slopes involving correlated nonnormals [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 922-935. DOI: 10.1016/j.ijrmms.2007.02.008.
[20] LI Lin, LIANG R Y, LIU Han-long. System reliability analysis for anchor-stabilised slopes considering stochastic corrosion of anchors [J]. Structure and Infrastructure Engineering, 2015, 11(10): 1294-1305. DOI: 10.1080/ 15732479.2014.963626.
[21] JIANG Shui-hua, HUANG Jin-song, ZHOU Chuang-bing. Efficient system reliability analysis of rock slopes based on Subset simulation [J]. Computers and Geotechnics, 2017, 82: 31-42. DOI: 10.1016/j.compgeo.2016.09.009.
[22] CHEN Xiao-gang, WANG Zu-yu. Rock slope stability analysis: Theory, methods and programs [M]. Beijing: China Water Power Press, 2005. (in Chinese)
[23] NIE Zhi-hong, WANG Xiang, HUANG Dong-liang, ZHAO Lian-heng. Fourier-shape-based reconstruction of rock joint profile with realistic unevenness and waviness features [J]. Journal of Central South University, 2019, 26(11): 3103- 3113. DOI: 10.1007/s11771-019-4239-8.
[24] BARTON N, BANDIS S, BAKHTAR K. Strength, deformation and conductivity coupling of rock joints [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1985, 22(3): 121-140. DOI: 10.1016/0148-9062(85)93227-9.
[25] BANDIS S C, LUMSDEN A C, BARTON N R. Experimental studies of scale effects on the shear behaviour of rock joints [J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1981, 18(1): 1-21. DOI: 10.1016/0148-9062(81)90262-x.
[26] BARTON N. Review of a new shear-strength criterion for rock joints [J]. Engineering Geology, 1973, 7(4): 287-332. DOI: 10.1016/0013-7952(73)90013-6.
[27] BARTON N. The shear strength of rock and rock joints [J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1976, 13(9): 255-279. DOI: 10.1016/0148-9062(76)90003-6.
[28] BAHAADDINI M, HAGAN P C, MITRA R, HEBBLEWHITE B K. Scale effect on the shear behaviour of rock joints based on a numerical study [J]. Engineering Geology, 2014, 181: 212-223. DOI: 10.1016/j.enggeo.2014. 07.018.
[29] OH J, CORDING E J, MOON T. A joint shear model incorporating small-scale and large-scale irregularities [J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 76: 78-87. DOI: 10.1016/j.ijrmms.2015. 02.011.
[30] WANG Gang, ZHANG Xue-peng, JIANG Yu-jing, WU Xue-zhen, WANG Shu-gang. Rate-dependent mechanical behavior of rough rock joints [J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 83: 231-240. DOI: 10.1016/j.ijrmms.2015.10.013.
[31] BASHA B, ASCE M, MOGHAL A A B. Load resistance factor design (LRFD) approach for reliability based seismic design of rock slopes against wedge failures [J]. Geotechnical Special Publication, 2013, 231: 582-591. DOI: 10.1061/9780784412787.061.
[32] KVELDSVIK V, NILSEN B, EINSTEIN H H, FARROK H N. Alternative approaches for analyses of a 100000 m3 rock slide based on Barton-Bandis shear strength criterion [J]. Landslides, 2008, 5(5): 161-176. DOI: 10.1007/s10346- 007-0096-x.
[33] DUZGUN H S B, BHASIN R. Probabilistic stability evaluation of Oppstadhornet rock slope, Norway [J]. Rock Mechanics and Rock Engineering, 2009, 42(5): 729-749. DOI: 10.1007/s00603-008-0011-3.
[34] ZHAO Lian-heng, ZUO Shi, LI Liang, LIN Yu-liang, ZHANG Ying-bin. System reliability analysis of plane slide rock slope using Barton-Bandis failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 88: 1-11. DOI: 10.1016/j.ijrmms.2016. 06.003.
[35] ZHAO Lian-heng, CAO Jing-yuan, ZHANG Ying-bin, LUO Qiang. Effect of hydraulic distribution on the stability of a plane slide rock slope under the nonlinear Barton-Bandis failure criterion [J]. Geomechanics & Engineering, 2015, 8(3): 391-414. DOI: 10.12989/gae.2015.8.3.391.
[36] ZHAO Lian-heng, JIAO Kang-fu, ZUO Shi, YU Cheng-hao, TANG Gao-peng. Pseudo-static stability analysis of wedges based on the nonlinear Barton-Bandis failure criterion [J]. Geomechanics and Engineering, 2020, 20(4): 287. DOI: 10.12989/gae.2020.20.4.287.
[37] BARTON N R, CHOUBEY V. The shear strength of rock joints in theory and practice [J]. Rock Mechanics, 1977, 10(1): 1-54. DOI: 10.1007/bf01261801.
[38] LIN Yu-liang, LI Ying-xin, ZHAO Lian-heng, YANG T. Investigation on seismic response of a three-stage soil slopesupported by anchor frame structure [J]. Journal of Central South University, 2020, 27(4): 1290-1305.
[39] LIN Yu-liang, ZHAO Lian-heng, YANG T, YANG Guo-lin, CHENG Xiao-bin. Investigation on seismic behavior of combined retaining structurewith different rock shapes [J]. Structural Engineering and Mechanics, 2020, 73(5): 599-612. DOI: 10.12989/sem.2020.73.5.000.
[40] KIM D H, GRATCHEV I, BALASUBRAMANIAM A S. Back analysis of a natural jointed rock slope based on the photogrammetry method [J]. Landslides, 2015, 12(1): 147-154. DOI: 10.1007/s10346-014-0528-3.
[41] SHARMA S, RAGHUVANSHI T, ANBALAGAN R. Plane failure analysis of rock slopes [J]. Geotechnical and Geological Engineering, 1995, 13(2): 105-111. DOI: 10.1007/BF00421876.
[42] ZUO Shi, ZHAO Lian-heng, DENG Dong-ping, WANG Zhi-bin, ZHAO Zhi-gang. Reliability back analysis of landslide shear strength parameters based on a general nonlinear failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 126: 104-189. DOI: 10.1016/j.ijrmms.2019.104189.
[43] JOHARI A, LARI A M. System probabilistic model of rock slope stability considering correlated failure modes [J]. Computers and Geotechnics, 2017, 81: 26-38. DOI: 10.1016/j.compgeo.2016.07.010.
[44] GUNTHER A, WIENHOFER J, KONIETZKY H. Automated mapping of rock slope geometry, kinematics and stability with RSS-GIS [J]. Natural Hazards, 2012, 61(1): 29-49. DOI: 10.1007/s11069-011-9771-2.
[45] NICHOL S L, HUNGR O, EVANS S G. Large-scale brittle and ductile toppling of rock slopes [J]. Canadian Geotechnical Journal, 2002, 39(4): 773-788. DOI: 10.1139/t02-027.
(Edited by HE Yun-bin)
中文导读
基于Barton-Bandis破坏准则的岩质边坡系统可靠度分析
摘要:由于岩体中存在大量结构面,岩质边坡普遍存在多种潜在失稳模式。本文基于非线性Barton-Bandis破坏准则研究了多失稳模式下的岩质边坡系统可靠度分析方法。分别给出了滑动失稳和倾覆失稳模式下的安全系数,并以一个坡顶和张拉裂缝倾斜的岩质边坡为例,验证了方法的有效性。通过分析,研究了结构面强度参数、坡体几何参数、锚固参数和裂隙形态等对岩质边坡系统可靠度的影响。
关键词:Barton-Bandis破坏准则;失稳模式;失效概率;岩质边坡;系统可靠度
Foundation item: Project(51978666) supported by the National Natural Science Foundation of China; Project(2018-123-040) supported by the Guizhou Provincial Department of Transportation Foundation, China; Project(2019zzts009) supported by the Fundamental Research Funds for the Central Universities, China
Received date: 2020-05-19; Accepted date: 2020-06-08
Corresponding author: ZHAO Lian-heng, PhD, Professor; Tel: +86-13755139425; E-mail: zhaolianheng@csu.edu.cn; ORCID: 0000- 0002-8406-5973

