简介概要

新型Fe-20Cr-30Ni-0.6Nb-2Al-Mo合金的热变形行为及本构模型

来源期刊：稀有金属2017年第2期

论文作者：罗锐程晓农徐桂芳郭顺郑琦朱晶晶

文章页码：132 - 139

关键词：奥氏体耐热合金;热压缩变形;应变量耦合;本构模型;

摘要：利用Gleeble-3500热力模拟试验机对新型奥氏体耐热（AFA）合金（Fe-20Cr-30Ni-0.6Nb-2Al-Mo）进行单道次压缩试验,研究了合金在1000¹150℃和0.01¹.00 s-1形变参数下的热变形行为。根据热压缩试验数据,绘制了不同形变参数下新合金的真应变-真应力曲线,并分析不同形变参数对合金微观组织的影响;基于Arrhenius方程通过线性回归建立高温形变条件下新材料的热变形本构方程;采用六次多项式对不同应变量下的材料常数进行拟合,建立耦合应变量因素的改进型本构方程。结果表明:在热变形过程中,合金的流变应力水平随着温度的提高而降低,随着应变速率的加快而增加;动态再结晶行为更容易发生在低应变速率和高变形温度的变形参数下;耦合应变量因素的本构模型预测合金的流变应力,预测值与压缩试验结果的相关系数为0.9856,平均相对误差仅3.4426%,可知改进型本构模型能较好地预测新型AFA合金在热变形过程中的流变应力。

网络首发时间: 2016-07-12 09:40

稀有金属 2017,41(02),132-139 DOI:10.13373/j.cnki.cjrm.xy15082801

新型Fe-20Cr-30Ni-0.6Nb-2Al-Mo合金的热变形行为及本构模型

罗锐程晓农徐桂芳郭顺郑琦朱晶晶

江苏大学材料科学与工程学院

摘要：

利用Gleeble-3500热力模拟试验机对新型奥氏体耐热(AFA)合金(Fe-20Cr-30Ni-0.6Nb-2Al-Mo)进行单道次压缩试验,研究了合金在1000~1150℃和0.01~1.00 s-1形变参数下的热变形行为。根据热压缩试验数据,绘制了不同形变参数下新合金的真应变-真应力曲线,并分析不同形变参数对合金微观组织的影响;基于Arrhenius方程通过线性回归建立高温形变条件下新材料的热变形本构方程;采用六次多项式对不同应变量下的材料常数进行拟合,建立耦合应变量因素的改进型本构方程。结果表明:在热变形过程中,合金的流变应力水平随着温度的提高而降低,随着应变速率的加快而增加;动态再结晶行为更容易发生在低应变速率和高变形温度的变形参数下;耦合应变量因素的本构模型预测合金的流变应力,预测值与压缩试验结果的相关系数为0.9856,平均相对误差仅3.4426%,可知改进型本构模型能较好地预测新型AFA合金在热变形过程中的流变应力。

关键词：

奥氏体耐热合金;热压缩变形;应变量耦合;本构模型;

中图分类号： TG132.3

作者简介：罗锐(1988-),男,江苏东台人,博士研究生,研究方向:高温合金的塑性加工;E-mail:luoruiweiyi@163.com;;程晓农,教授;电话:0511-88780006;E-mail:xncheng6009@sina.com;

收稿日期：2015-09-02

基金：“十二五”国家高技术研究发展计划(863计划)重大项目(2012AA03A501);江苏省2014年度普通高校研究生科研创新计划项目(KYLX_1027);江苏省2015度普通高校研究生科研创新计划项目(KYLX15_1057)资助;

Constitutive Modeling for Elevated Temperature Flow Behavior of Fe-20Cr-30Ni-0.6Nb-2Al-Mo Alloy

Luo Rui Cheng Xiaonong Xu Guifang Guo Shun Zheng Qi Zhu Jingjing

School of Materials Science and Engineering,Jiangsu University

Abstract：

To study the flow stress behavior of an AFA-type alloy,Fe-20Cr-30Ni-0.6Nb-2Al-Mo(%,atom fraction),isothermal hot compression tests were performed at a temperature range of 1000 ~ 1150 ℃ with strain rates of 0.01 ~ 1.00 s-1using Gleeble 3500thermal-mechanical simulator.Based on the data of hot compression tests,the flow stress curves of this alloy under different deformation conditions were plotted,and the effects of hot deformation conditions on the microstructure were analyzed.The constitutive model considering the compensation of strain for predicting the flow stress of AFA alloy under all test conditions was developed on the basis of Arrhenius-type equation.The functional relations between material constants in the model and strain were identified by sixth order polynomial fitting.Experimental results showed that the flow stress decreased with the increase of temperature at the same strain rate,while increased with the increase of strain rate at the same deformation temperature during high temperature compression deformation.The dynamic recrystallization was more likely to occur at a low strain rate and high deformation temperature.The accuracy of the developed model was evaluated using standard statistical parameters such as correlation coefficient and average absolute relative error.It suggested that this developed constitutive equation could accurately predict high temperature flow behaviors of Fe-20Cr-30Ni-0.6Nb-2Al-Mo alloy and could be used to numerically analyze the hot deformation process of this alloy.

Keyword：

austenitic heat resistant alloy; hot compression deformation; compensation of strain; constitutive modeling;

Received： 2015-09-02

近年来,一种表面自发形成Al₂O₃保护膜层的新型奥氏体耐热合金(AFA)被成功开发出来^[1,2,3,4]。这类新型耐热合金含有一定量的Al,Nb,在650~800℃水蒸气条件下,由于材料表面形成防护型Al₂O₃氧化膜增强了基材的高温抗氧化性,同时纳米级Laves相及MC型碳化物的弥散析出有效钉扎位错运动是提高材料蠕变强化能力的主要因素。

目前,关于新型AFA合金的研究方向大多集中于高温抗氧化性能和蠕变性能^[2,3,4,5],而热变形行为对合金的组织性能控制具有十分重要的工程意义。热变形过程中,材料的流变应力值与变形参数之间存在着较为复杂的关系。通常采用Arrhenius型方程应用数理统计方法建立金属材料的本构关系,此类方程一般用于稳态应力或某一应变量所对应应力值来描述应变速率、变形温度与应力之间的关系,迄今已有大量金属材料基于这种方程建立起热变形本构关系^[6,7,8,9]。然而上述建立的本构模型并未考虑应变量因素的影响,这对于预测材料在实际热变形过程中的流变应力值存在较大的误差。针对上述问题,Slooff等^[10]耦合应变量因素嵌入上述传统Arrhenius方程中,建立由应变量决定材料常数的双曲线正弦本构方程,并精准预测了不同形变参数下镁合金Mg-Al4-Zn1的流变应力。鉴于这种改进型本构模型,近年来已成功构建多数金属材料的本构方程^{[11,12,13,14,15]}。

基于此本文分析了不同形变参数对一种新型AFA合金(Fe-20Cr-30Ni-0.6Nb-2Al-Mo)微观组织的影响,利用传统的Arrhenius方程求得表观材料常数,得到某一应变量所对应的应力与变形参数之间的关系。考虑应变量的因素,计算不同应变量下热变形激活能等参数,由于AFA合金化程度较高,发现材料参数与应变量之间存在比6061铝合金^[11]、H62黄铜^[13]、35Mn2钢^[14]及10Cr Mo WNb钢^[15]更为复杂的非线性关系。因此本文采用基于最小二乘法的多项式拟合,并取比上述材料更高的拟合次数,建立耦合应变量因素的本构模型。最后分别引入相关线性系数和平均相对误差,以评估典型AFA合金的热变形本构模型在试验范围内预测流变应力的精确性。

1 实验

将本试验所使用的这种新型AFA合金(Fe-20Cr-30Ni-0.6Nb-2Al-Mo)加工成尺寸为直径8 mm,长12 mm的圆棒,要求材料表面光洁且端面平行。在Gleeble-3500热力模拟试验机上进行等温单道次压缩试验,为防止试样在加热过程中表面发生氧化,热模拟试验均在真空模式下进行。试样与压缩岾头之间添加一层0.05 mm厚度坦片,减少端部摩擦造成的鼓肚效应。

压缩试验开始控制程序设定试样以10℃·s^-1的速率加热至1150℃保温10 min,再以5℃·s^-1的冷却速率至变形温度,保温30 s使试样温度均匀化后进行压缩变形。试验变形温度分别为1000,1050,1100和1150℃;应变速率分别为0.01,0.10和1.00 s^-1;压缩变形量为55%。为研究形变参数对材料微观组织的影响,在压缩试验完成后立即淬火保留高温组织,沿平行于压缩轴线方向切割试样。经抛光、腐蚀处理后,在蔡司金相显微镜(OM)下进行观察分析。根据压缩试验获得的不同形变条件下的流变应力,绘制合金的真应力-真应变曲线。以传统的Arrhenius型方程构建Fe-20Cr-30Ni-0.6Nb-2Al-Mo合金的本构方程,考虑应变量对热变形材料常数的影响,建立耦合应变量因素的改进型本构方程。

2 结果与讨论

2.1 真应力-真应变曲线

不同变形参数下,合金的流变应力曲线如图1所示,可知合金流变应力值明显受制于变形温度和应变速率。当应变速率一定,流变应力水平随变形温度的提高而降低(图1(a)),由于变形温度的持续走高,受热激活影响致使位错运动的阻力削弱,空位和间隙原子等点缺陷更加活跃^[16],进而导致应力水平降低;而变形温度一定,应变速率的加速导致流变应力水平上升(图1(b))。应变速率的加速使得位错密度增速陡升,必然导致位错缠结和胞状亚结构数量变多,加工硬化现象愈发明显,应力水平也随之升高。较低应变速率下,合金的流变应力出现明显软化现象,流变应力随着应变量的增大,迅速上升达至峰值点后,呈现两种趋势:一种是峰值点后出现下降趋势,并最终趋于稳态。这是典型的完全再结晶行为,动态再结晶产生的软化机制完全抵消加工硬化效应并占据主导;而另一种在峰值点后曲线趋于平稳态,未出现流变应力下降趋势,呈现动态回复特征。这可能是加工硬化和动态软化的相互作用,使得应力趋于一个与峰值应力较为接近值,或合金在热变形过程中只发生了部分再结晶现象。

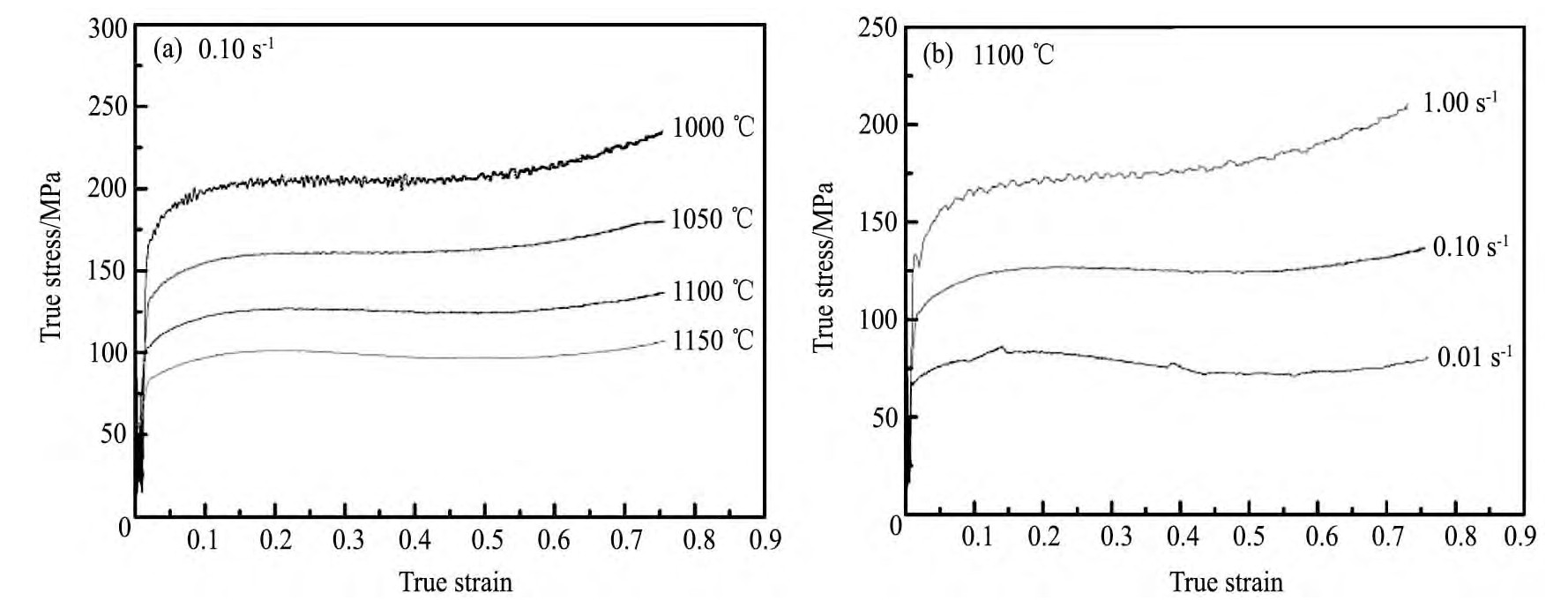
图1 Fe-20Cr-30Ni-0.6Nb-2Al-Mo合金在不同形变参数下的真应力-真应变曲线Fig.1 Typical flow stress curves of Fe-20Cr-30Ni-0.6Nb-2Al-Mo at various deformation temperatures(a)and strain rates(b)

2.2 微观组织分析

当应变速率为0.01 s^-1,不同变形温度下合金的显微组织如图2所示。当变形温度为1000℃时,原始奥氏体组织沿着变形方向被严重拉长,并出现不规则的“锯齿状”晶界及少量细小的再结晶晶粒,这种“锯齿状”结构为动态再结晶晶粒的形核提供了条件。随着变形温度升至1050℃,再结晶晶粒形核并长大,逐渐取代原始奥氏体组织,再结晶组织所占比例明显增加,但仍存在少量拉长的形变奥氏体组织。而当变形温度达至1100℃,动态再结晶晶粒已经完全取代原始奥氏体晶粒,且晶粒粗化明显。在应变速率和变形程度相同时,合金动态再结晶体积分数随着变形温度的升高而增大。随着变形温度的攀升,晶界空位的扩散愈发容易,这也促使小角度晶界向大角度晶界的转变,有利于动态再结晶过程的完成。

图3为合金在变形温度1150℃,不同应变速率下的金相组织。当速率为1.00 s^-1时,发生了不完全动态再结晶,形变组织中残留了少量拉长的原始奥氏体晶粒。随着应变速率减慢至0.10 s^-1,再结晶组织已基本吞噬原始组织,动态再结晶行为趋于完整。应变速率进一步降低至0.01 s^-1,发生完全动态再结晶,再结晶晶粒尺寸也随应变速率的降低也有一定程度粗化。这是由于亚结构容易在低应变速率下形成,通过动态再结晶的形核、长大方式,形变储存能可迅速实现释放;当应变速率提高,导致变形时间大幅缩短且变形程度剧烈,再结晶晶粒在形核后就可能经历变形,从内部形成位错,这也降低再结晶核心与周围形变晶粒间的应变梯度^[17],因而导致再结晶晶粒的长大也不明显。

图2 应变速率为0.01 s-1,不同变形温度下合金的显微组织Fig.2 OM images of microstructures of samples hot deformed at 0.01 s-1

(a)1000℃;(b)1050℃;(c)1100℃

图3 变形温度为1150℃,不同应变速率下材料的显微组织Fig.3 OM images of microstructures of samples hot deformed at 1150℃

(a)0.01 s^-1;(b)0.10 s^-1;(c)1.00 s^-1

2.3 传统本构模型的构建

热变形过程中,合金的流变应力主要取决于变形温度和应变速率。通常采用双曲线正弦方程描述这三者之间的关系:

式中,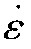 为应变速率,s^-1;Q为热变形激活能,k J·mol^-1;T为热力学温度,K;R为气体常数,8.314 J·(mol·K)^-1;σ为峰值应力、稳态应力或某一指定应变时对应的流动应力,本文σ值均采用以应变量为0.5时所对应的流变应力值;A,n₁,n,α,β均为热变形材料常数,α=β/n₁。F(σ)中的3个关系式分别适用于低应力水平、高应力水平和所有应力水平。基于材料的真应力-真应变曲线可知,不同变形条件下合金的流变应力范围较大(70~300 MPa),因此更适用于双曲正弦形式为基础构建材料的本构关系。变形温度和应该速率对材料高温塑性变形的影响可用一个Z参数来表示:

Z为Zener-Hollomon参数,这一参数与流变应力之间服从如下关系:

对上述式子分别取自然对数,并通过线性拟合方法^[6,7,8,9],分别建立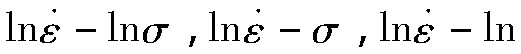 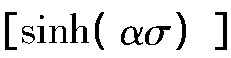,ln[sinh(ασ)]-(10³/T),ln Z-ln[sinh(ασ)]的线性关系如图4所示,所得斜率推出材料常数α=0.007107,n=4.11135,Q=397.9981 k J·mol^-1,A=1.29×10¹⁴。进而可得到这一种AFA合金在变形温度1000~1150℃和应变速率0.01~1.00 s^-1条件下的热变形本构方程:

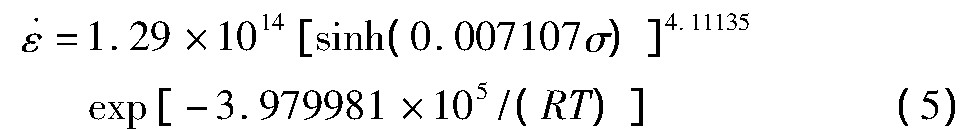
2.4 建立耦合应变量因素的改进型本构模型

根据材料的流变应力曲线可知,不同应变量对流变应力值影响显著,而传统的Arrhenius型方程则忽略了应变量因素,这对于预测实际工程中材料流变应力存在较大误差。因此建立耦合应变量因素的本构模型,对预测材料在形变过程中真实流变应力值具有重要的工程意义。本文基于传统Arrhenius型本构方程,求得不同应变量(0.05~0.75,间隔0.025)所对应的热变形材料常数(α,n,Q及ln A),假设合金的材料常数均为关于应变量的多项式函数,如公式(6)所示。相关文献常采用四或五次多项式对材料常数进行拟合处理^{[11,12,13,14,15]},由于AFA合金化程度较高,其特殊的热变形特征导致材料参数与应变量之间的非线性关系(图5)较6061铝合金、H62黄铜、35Mn2钢及10Cr Mo WNb钢更为复杂。因此本文采用更高的拟合次数,但提高拟合次数会出现“Runge现象”或拟合精度并不能有效改善^[16],本文分别对比四次、五次和六次多项式拟合结果,如图5所示利用六次多项式拟合其数据偏离拟合曲线最小,表现出较好的拟合效果。表1数据则定量分析了不同拟合次数的结果,可知采用六次多项式拟合材料常数与应变量的关系表现出最优异的拟合精度,其拟合系数如表2所示。

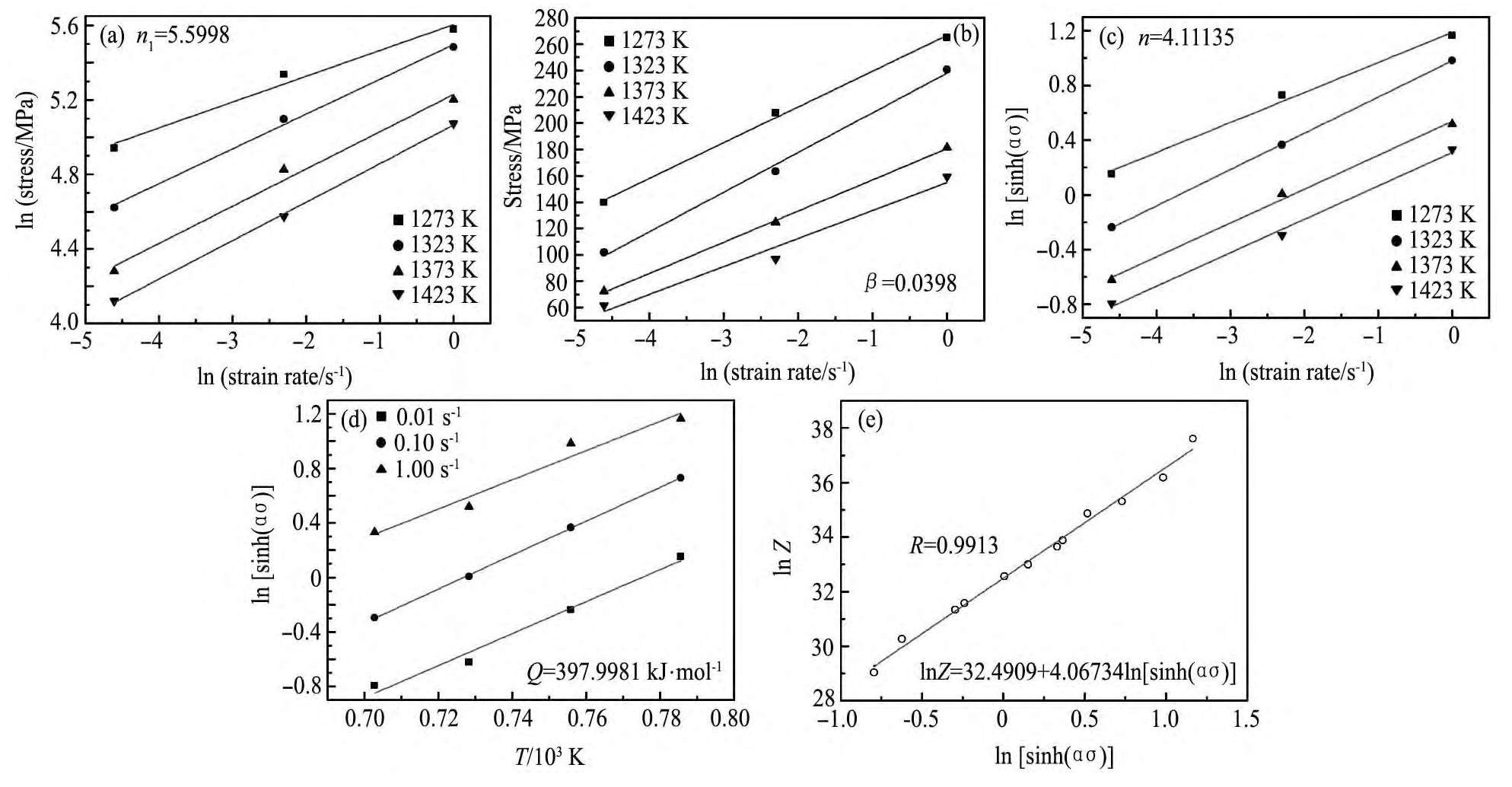
图4不同参数之间的线性拟合图Fig.4 Plots of(a)lnε-lnσ,(b)lnε-σ,(c)lnε-ln[sinh(ασ)],(d)ln[sinh(ασ)]-(10³/T),(e)ln Z-ln[sinh(ασ)]for Fe-20Cr-30Ni-0.6Nb-2Al-Mo at strain of 0.5

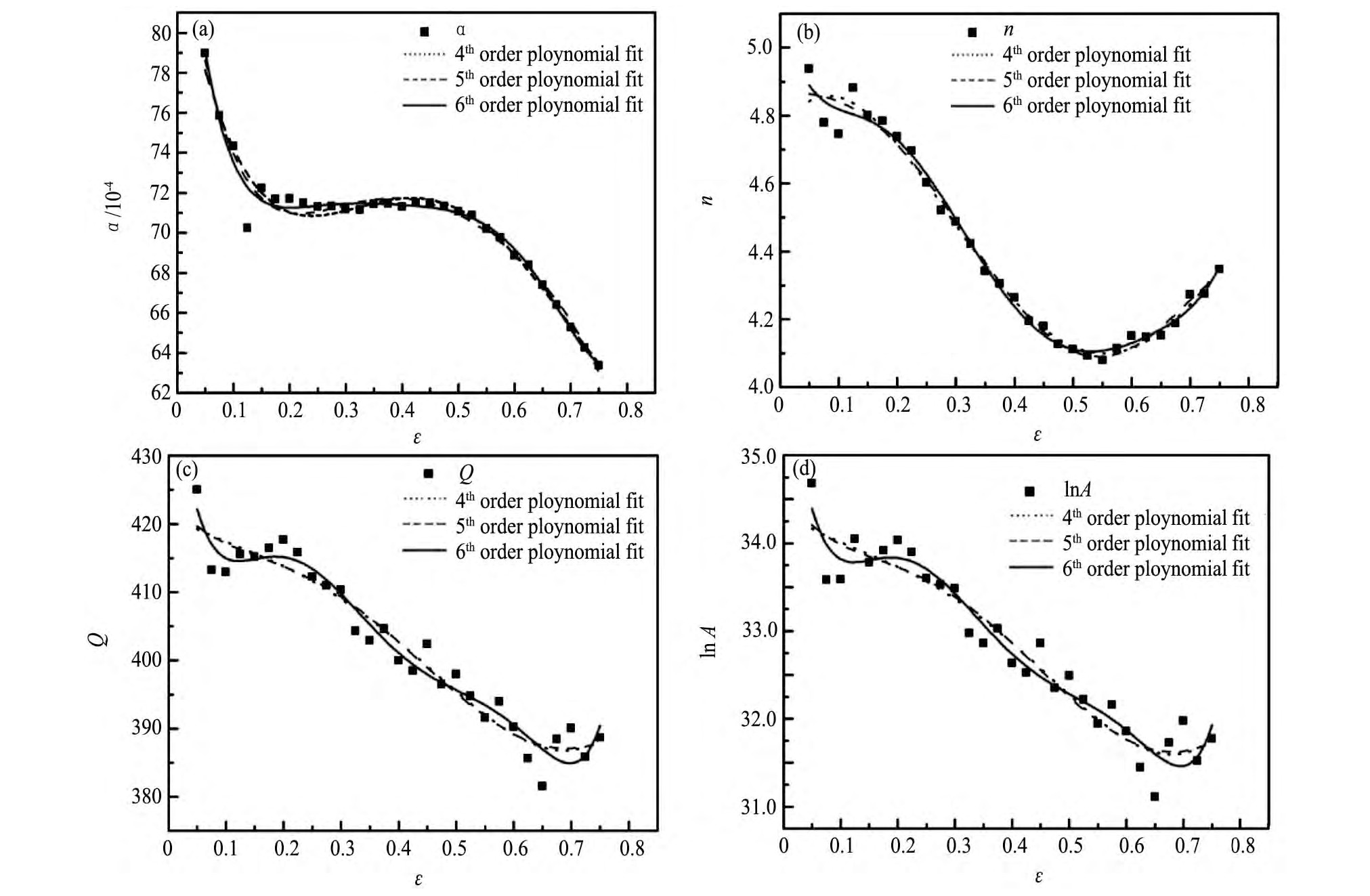
图5 合金的材料常数与应变量之间的关系Fig.5 Variation of material constantsα(a),n(b),Q(c),ln A(d)of constitutive models of hot deformation of AFA at different values of strain

表1 AFA不锈钢的材料常数(α,n,Q及ln A)的拟合结果Table 1Regression fitting coefficients of material con-stants(α,n,Q and ln A) 下载原图

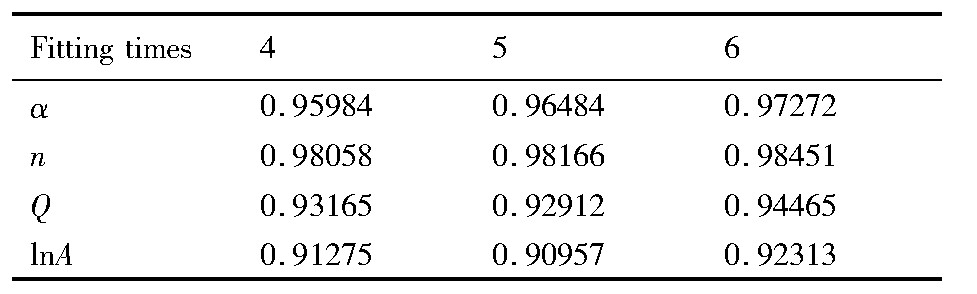
表1 AFA不锈钢的材料常数(α,n,Q及ln A)的拟合结果Table 1Regression fitting coefficients of material con-stants(α,n,Q and ln A)

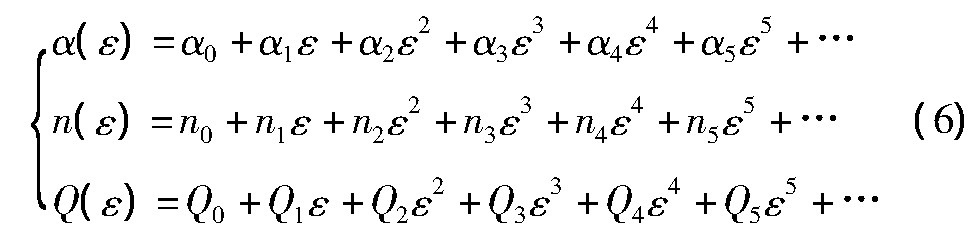
由公式(4)可知:

根据双曲线正弦函数的定义,流变应力推算服从如下关系式:

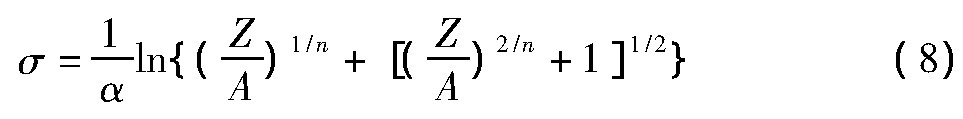
进而得到不同应变(ε)的流变应力:

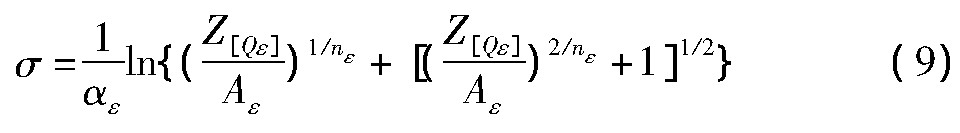
当材料常数(α,n,Q及ln A)被确定,不同应变量下的流变应力值即被确定。利用公式(9)可以预测不同应变速率、形变温度及应变量下的这种AFA不锈钢的流变应力值。

2.5 改进型本构模型的验证

为验证上述本构模型预测AFA合金在热变形过程中流变应力的准确性,将不同应变速率、不同应变温度及不同应变量所构建的本构模型关于流变应力的计算值共计348组数据,与实验所获得流变应力值进行对比,如图6所示,可知实验条件范围内本构模型的流变应力预测值与压缩试验获得流变应力曲线吻合良好。而当应变速率达至1.00s^-1时,预测值与实际值之间的偏差较为明显,这是由于高应变速率条件下,热变过程发生了绝热升温现象^[18],导致实际温度明显增加,从而诱发DRX等软化现象,致使实际流变应力值与预测值出现明显偏差。

为进一步定量分析本构模型的精确度,本文分析本构模型预测值与实验值的相关性,如图7所示,相关系数R为0.9856,可知预测值与实验值之间线性相关性较强。R值通常由于表明实验值与计算值的线性关系的强弱,但系数高并不一定代表符合性好,可能出现数据全部偏低或偏高现象。为此本文引入平均相对误差δ:

表2 六次多项式拟合系数Table 2 Coefficients of polynomial for material constants(α,n,Q and ln A) 下载原图

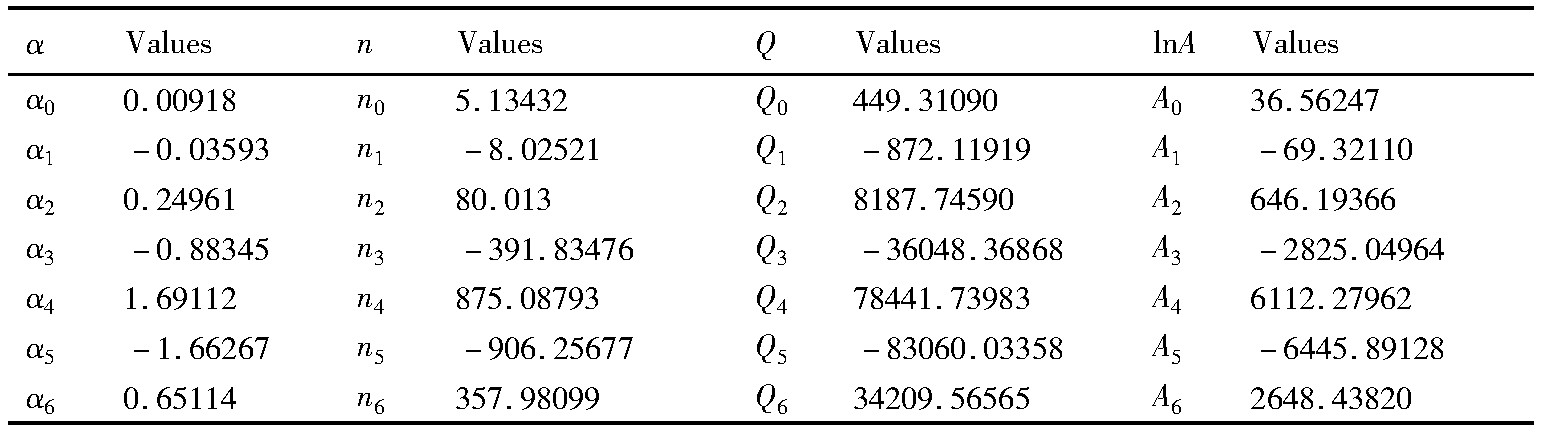
表2 六次多项式拟合系数Table 2 Coefficients of polynomial for material constants(α,n,Q and ln A)

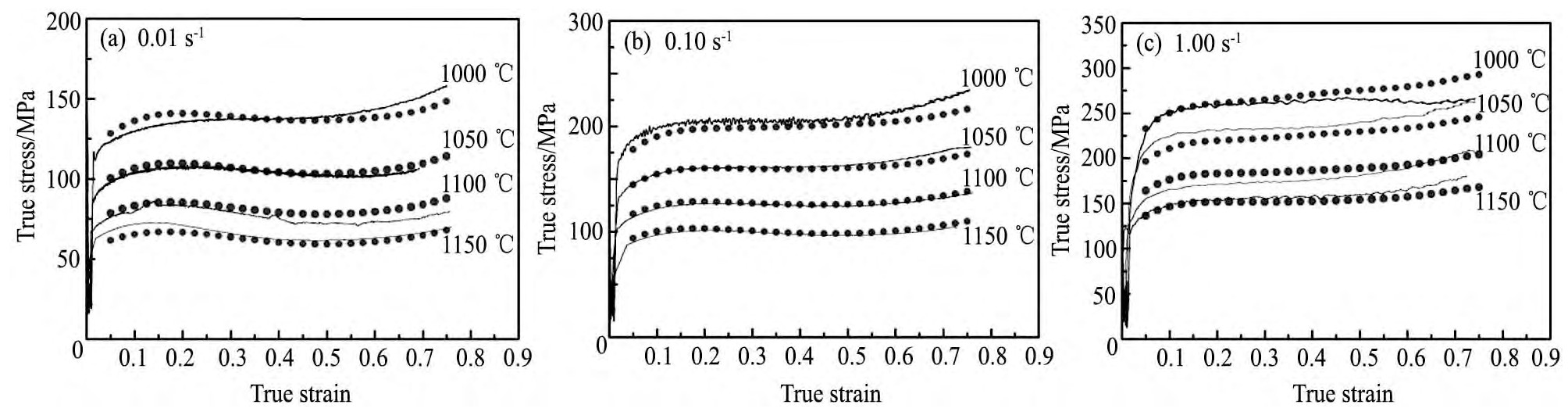
图6 改进型本构模型预测流变应力曲线与压缩试验数据对比Fig.6 Comparisons between predicted and experimental flow stress curves at strain rates of(a)0.01 s-1,(b)0.10 s-1,(c)1.00 s-1

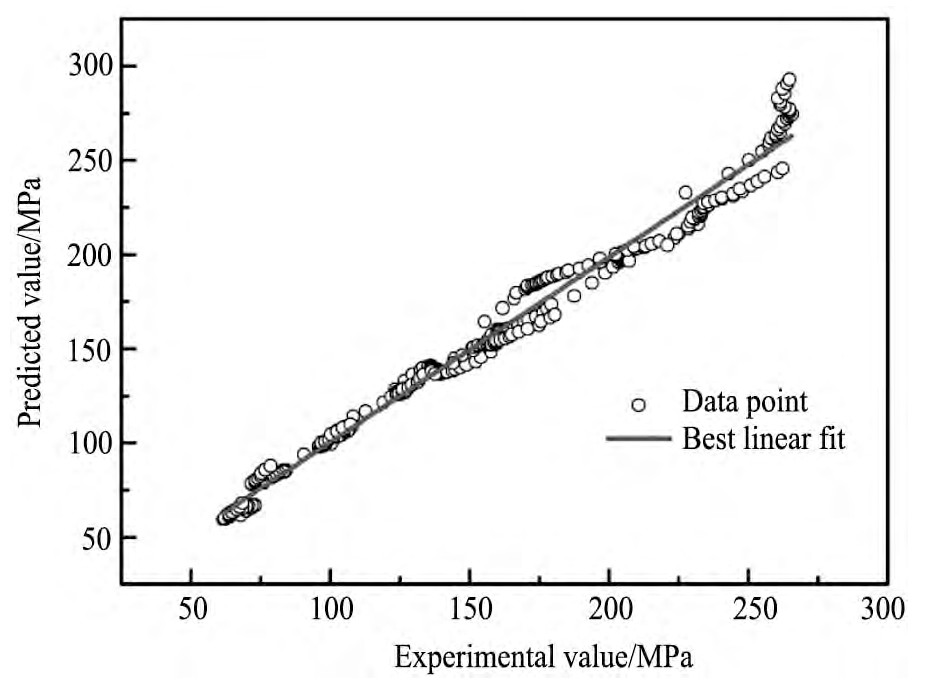
图7 改进型本构模型预测流变应力与压缩试验数据的相关性Fig.7 Correlation between predicted and experimental values at current experimental conditions

式中N为所采集的分析数据点个数,σ_e为压缩试验所获取的流变应力值,σ_p为本构模型预测流变应力值。由于这种平均相对误差对于本构模型的预测性的分析是无偏差,更能定量评价本构模型的预测能力。计算可知其平均相对误差仅为3.4426%,结合线性相关性R值说明所建立的AFA合金的本构模型具有良好的预测能力。

为探究本文所采用的六次多项式拟合材料常数对比四次多项式拟合是否具有更高的预测精确度,将对不同拟合方式所得到的本构模型的预测能力进行比较,见表3所示。由相关系数R值,可知六次多项式拟合所得到的预测值与实验值线性关系更为强烈;利用四次多项式拟合时δ为5.1642%,而六次多形式拟合时δ仅为3.4426%;采用六次多项式拟合材料常数,预测相对误差小于6%和10%的变形条件分别占试验条件范围的85.34%和99.14%,四次多项式拟合时则为77.01%和90.23%。综合对比不同拟合次数所得到的本构模型的预测精度,表明新型Fe-20Cr-30Ni-0.6Nb-2Al-Mo合金采用六次多项式拟合材料常数所构建的本构模型具有更高的预测精度,这种耦合应变量因素的本构模型适合此合金在实际工程应用中的数值模拟。

表3 本构模型预测流变应力的精度对比Table 3 Comparison of prediction accuracy of equation 下载原图

表3 本构模型预测流变应力的精度对比Table 3 Comparison of prediction accuracy of equation

3 结论

1.典型AFA合金在热变形过程中,材料流变应力明显受制于变形温度和应变速率。应力水平值随着变形温度的升高而降低,随应变速率的加快而增大。

2.基于传统的Arrhenius方程通过线性回归建立高温形变条件下新型Fe-20Cr-30Ni-0.6Nb-2AlMo合金的热变形本构方程,其方程式为:

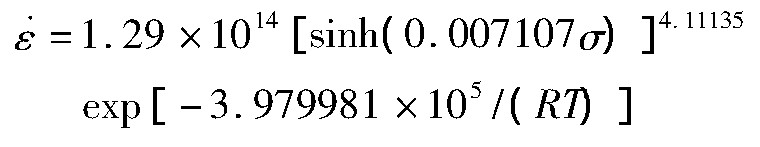
3.计算各应变量下热变形激活能等材料常数,发现材料常数与应变量之间的关系可以用六次多项式函数进行较好的表达。建立耦合应变量因素的本构模型,并预测合金的流变应力值。预测结果表明预测值与实际压缩数据之间的相关系数达至0.9856,平均相对误差仅3.4426%,可知这种改进型本构模型在试验条件范围内能较好地预测合金的流变应力。