J. Cent. South Univ. (2012) 19: 1846-1852 

DOI: 10.1007/s11771-012-1218-8

Mechanical model of breaking rock and force characteristic of disc cutter

XIA Yi-min(夏毅敏)¹, OUYANG Tao(欧阳涛)^{1, 2}, ZHANG Xin-ming(张新明)³, LUO De-zhi(罗德志)¹

1. State Key Laboratory of High Performance Complex Manufacturing

(Central South University), Changsha 410083, China;

2. China Nerin Engineering Co., Ltd, Nanchang 330000, China;

3. School of Materials Science and Engineering, Central South University, Changsha 410083, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: According to the cutting characteristics of progressive spiral movement by rotary cutting of the disc cutter, using the broken theory of interaction of compression and shearing, the three-axis force rotary cutting mechanical model of disc cutter was established and the influence of installation radius, the phase difference and the cutter space on the mechanics of disc cutter were analyzed. The results show that on the same radial line of tunneling interface, the boring distance of cutting tools installed on a different radius is not equal. The cutting radial line of tunneling interface is a polyline and its height is determined by phase angle and penetration of cutting tools. Both phase difference and the installation radius between adjacent disc cutters have little effect on the vertical force and rolling force, but increase with the increase in cutter spacing. In addition, when increasing phase difference and cutter space bilaterally, and reducing installation radius simultaneously, the lateral force would be improved. Related results have been verified on100 t rotary tool cutting test platform.

Key words: mechanical model; phase angle; installation radius; cutter space; disc cutter
 

1 Introduction

Shield has been widely used in tunnel construction of railway, highway and subway. Disc cutter, with its large load and high efficiency of rock breaking, has become the main tool of shield [1-2]. The adjacent disc cutters are not installed on the same location, but installed in different bars of the cutter because of the cutter structure, and the position parameters of adjacent disc cutters have significant effects on cutting process [3]. A lot of scholars have done much work on studying the rock-breaking process of disc cutters [4-9]. They presented corresponding formulas applied in engineering construction. These studies provide theoretical and experimental basis for reasonable design and arrangement of disc cutter. However, these mechanical models of disc cutter are mainly based on linear cutting, and further discussion on the difference of these models between linear and rotary cutting have not been conducted yet. From the experience of engineering and experiments, there are significant differences between linear cutting and rotary cutting. Disc cutter suffers great lateral force during rotary cutting, and the phenomena of teeth collapsing and cutter ring falling off happen constantly [10-11]. Studying regular impact of layout parameters on cutting process can provide important guiding significance for understanding arrangement rules, setting layout parameters and enhancing processing performance of the disc cutter [12-13]. Based on the analysis of the effect of installation parameters on disc cutter during rotary cutting process, it can be concluded that the cutting rock surface is not flat and the rock-breaking amount between inner side and outer side of disc cutter is not identical.

2 Factors of disc cutter cutting

2.1    Impact of phase angle on rotary cutting

The layout of the disc cutters from No. 10 to No. 15 of a typical composite shield cutter is shown in Fig. 1 [14]. Phase difference, which is dependent on rotary sequence of cutters, exists between adjacent disc cutters, for example, No. 11 disc cutter cuts the area which belongs to the disc cutter of No. 10, and the disc cutter of No. 11 needs to go through 180° out of phase to move to this position. Assuming that t is the time required for the cutter to revolve within one cycle, the time of the No. 11 disc cutter moving to the position is t/2. Along moving forward of the shield cutter, No. 11 cutter will go through the radial line and move forward to a certain depth, after No. 10 cutter goes through the radial line. Therefore, any radial line on tunneling interface is not a straight line, but a polyline. Taking the position of No. 10 disc cutter on the spoke as an example, the radial line on tunneling interface is shown in Fig .2.

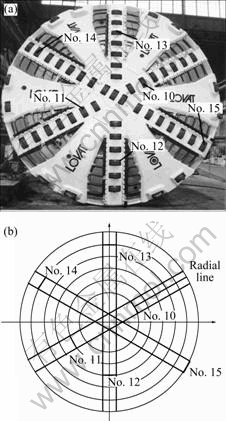
Fig. 1 Layout of disc cutters form No. 10 to No. 15 of one cutter

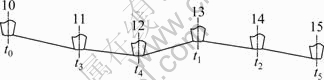
Fig. 2 Leveling schematic diagram of one radial line in tunneling interface

Consequently, the phase difference between adjacent disc cutters can cause one boundary line of the shear plane to transform into polyline from straight line. And then, the area of shear plane becomes larger, and larger area leads to larger shear force, thereby it affects three components of cutting forces on disc cutter.

2.2    Impact of installation radius on rotary cutting

The larger the installation radius of disc cutter, the more the broken rock would be got. As to the same disc cutter, the amount of broken rock from outside of disc cutter is larger than that from inside, that is to say, the outside of disc cutter would suffer greater shear force, and this shear force is a part of lateral force. Through the cutter trajectory analysis, the difference of broken rock between inside and outside of disc cutter for single cutting is obtained, as indicated in Fig. 3.

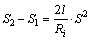                              (1)

where S₂ and S₁ are the outer area and the inside area, respectively; R_i is the installation radius of disc cutter; S is the disc cutter space; l is the single pressed arc length of disc cutter. Because the cutting depth is a fixed value, the single pressed arc length is also a fixed value.

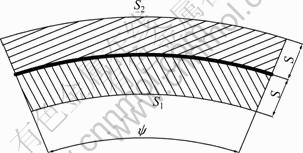
Fig.3 Rock breaking schematic diagram of disc cutter inside and outside

If the cutter space is constant, the difference of broken rock between inside and outside of disc cutter is larger when installation radius of disc cutter is smaller, which means if it is closer to inner of cutter, the lateral force suffered by disc cutter is greater.

2.3 Impact of cutter space on rotary cutting

The layout of cutter space is often related to cutting geological conditions in engineering, and different types of rock need different cutter spaces. When the rock is harder, the cutter space is usually smaller; when the rock is softer, the cutter space is relatively larger. It can be seen that cutter space plays an important role in shield tunneling. If cutter space is large, the amount of broken rock by adjacent disc cutters would be large, and then the force of rotary cutting is also great. When the cutter space is extremely large, the rock in adjacent disc cutters cannot be sufficiently broken, accordingly, this part of rock would prevent the shield moving forward.

3 Mechanical model of rotary cutting for any disc cutter

Different models are established for the study of linear rock-breaking theory of disc cutter. The typical example is the Evans’ pressing and breaking theory [15], which shows that, during the occurrence of squeezing rock crushing, the pressing force is proportional to the broken funnel pit area and the compressive strength. Then, ROSTAMI and OZDEMIR [16] bring forward the theory of combined effects of compression and broken shear, which shows that compression and broken shear exist in the rock-breaking process simultaneously. Based on both Evans’ model and the linear cutting model, the three-axis force rotary cutting mechanical model of disc cutter is established with the effect of blade width and cutter space on rock-breaking mechanism. When the disc cutter does rotary cutting, the force consists of the vertical force in the direction of pressing rock, the rolling force in the tangent direction and the lateral force produced by shearing and breaking rock of cutter tools.

3.1 Vertical force calculation of rotary cutting of disc cutter

The calculation of vertical force is divided into two parts: One is the pressing force needed by squeezing and breaking the rock below disc cutter, and another part is the force which shears and breaks the rock located on adjacent disc cutters [17-18].

1) Calculation of F_V1

F_V1 is the vertical component of the force acting on rock suffering crushing failure. Due to extrusion and rupture, the rock in contact with disc cutter reaches the single-axial compressive strength. F_V1 is calculated as follows:

                          (2)

where E is the area of the rock by squeezing and breaking; σ_c is the single-axial compressive strength of rock; ω is the angle between the normal direction of integral area and the vertical direction.

F_V1 is the product of projected area of A in the vertical direction and single-axial compressive strength of rock. To simplify the calculation, the projected area is simplified as ??the isosceles trapezoid, as shown in Fig. 4.

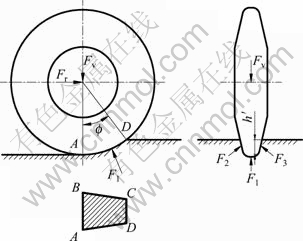
Fig. 4 Projection of rock surface damaged by squeezing in vertical direction

The projected area increases with respect to cutting depth. When the cutting depth of disc cutter satisfies h≤r(1-sinθ), then 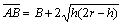,  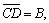so

 (3)

where R is the radius of disc cutter; r is the corner radius of cutting edge; B is the top width of cutting edge; f is the contact angle of disc cutter with rock, and f=arccosR-h/R.

When the cutting depth of disc cutter satisfies h≤r(1-sinθ), it means that cutting depth has passed over the boundary point between transition arc and line segment, and the incremental depth of cutting edge is 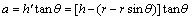. The nose angle of disc cutting used in engineering is commonly 10° at present, and then the tangent of nose angle is only about 0.1. So, even if the cutting depth passes over the transition arc, the impact on the hemline of the isosceles trapezoid like funnel-shaped pit is very little. Therefore, when the cutting depth passes over the boundary point between transition arc and line segment, the calculation of the trapezoidal area is still based on the formula mentioned above.

2) Calculation of F_V2

F_V2 is the vertical force required by making the rock located between adjacent disc cutters broken. It is believed that the rock between adjacent disc cutters is broken by shear force, and the shear force is proportional to the shear strength of rock, calculated by F=τ·S. The shear force needed by shearing and breaking the rock is calculated firstly, and then is converted to F by F_V2.

The phase difference between one disc cutter and its medial adjacent disc cutter is β₁, and the cutter space is S. The phase difference between the disc cutter and its lateral adjacent disc cutter is β₂, and then the shear force required by breaking the rock between disc cutter and the lateral adjacent disc cutter is F_r1:

     (4)

where τ is shear strength of rock; S is cutter space; R_i is the installation radius of No. i disc cutter when installing on the cutter; B is the top width of cutting edge; ψ is the angle between two sidelines on the cutter during single

cutting, and .

Then, the shear force required by breaking the rock between the disc cutter and the medial adjacent disc cutter is F_r2:

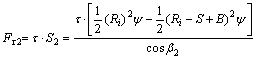     (5)

where β₂ is the phase difference between the disc cutter and the medial adjacent disc cutter.

According to the angular relationship between shear force and vertical force, the medial shear force and the lateral shear force of adjacent disc cutters both have vertical components, and then F_V2 can be written as F_V2=(F_r1+F_r2)·tanθ, that is

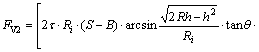
           (6)

Then, the vertical force of any disc cutter during rotary cutting is

 (7)

3.2 Lateral force calculation of rotary cutting of disc cutter

Based on the process of the vertical force calculation, because there are phenomena of breaking rock on both inside and outside of disc cutter, it can be found that the lateral force of disc cutter is an actually unbalanced force on inside and outside during rotary cutting:

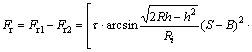
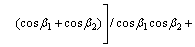
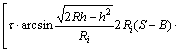
             (8)

3.3 Rolling force calculation of rotary cutting of disc cutter

The rolling force of disc cutter during rotary cutting is the friction suffered by disc cutter. At present, the rolling force can be usually got by the product of cutting coefficient and vertical force of disc cutter during rotary cutting, and the cutting coefficient C is

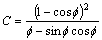                            (9)

                                 (10)

4 Experimental study of model

4.1 Experimental principle

This cutting model is verified by 100 t rotary tool cutting test platform, as shown in Fig. 5. The main propulsion cylinder promotes the disc cutter to press into soil, and the rotary motor drives the plate with material to do rotary motion, then the disc cutter completes rotary cutting. Cutting parameters, i.e. cutting radius, phase angle and knife spacing, can be changed through adjusting rotary cutter layout. In the experimental process, the forces of disc cutter in different cutting conditions were recorded by strain gauge pasted in the turret, then the testing signal was transferred to acquisition card by the dynamic strain instrument, finally the data were displayed on computer, as shown in Fig. 6.

Fig. 5 Rotary cutting experiment platform

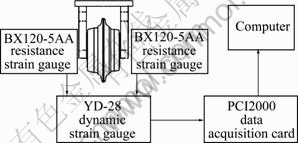
Fig. 6 Experimental principle diagram

4.2 Experimental process

The model is verified through changing cutting depth, cutter spacing, phase angle and installation radius during experiments, and the corresponding cutting variables are listed in Table 1. The experimental disc cutter radius is 108 mm and blade width is 6.5 mm. To reduce the randomness and improve the repeatability of the experiment, cement mortar is used as cutting material. The related parameters of the standard sample are listed in Table 2, which are measured by the mechanical testing center.

Table 1 Cutting variables

Table 2 Material parameters of cement mortar

4.3 Analysis of experimental results

Three-axis cutting force can be obtained by three steps. Firstly, the signals of three-axis cutting forces produced by rotary cutters are firstly transmitted to computer by stain gauges fixed on knife holders. Then, three-axis cutting force is calibrated through pressing machines, followed by signal transformation.

Figure 7 shows the result of the experimental data compared with the theoretical value under different cutting conditions. It can be seen that, the calculated value of lateral force is in good agreement with the experimental value, and the largest error is 8.77%. The largest error between the calculated value of vertical force and the experimental value is 11.2%, and it appears when the cutter space is 72 mm, for the reason that in the course of the experiment, the rock located between adjacent disc cutters is not completely cut, and the cutter space is too large, then the phacolith appears, which makes the model value relatively larger.
 

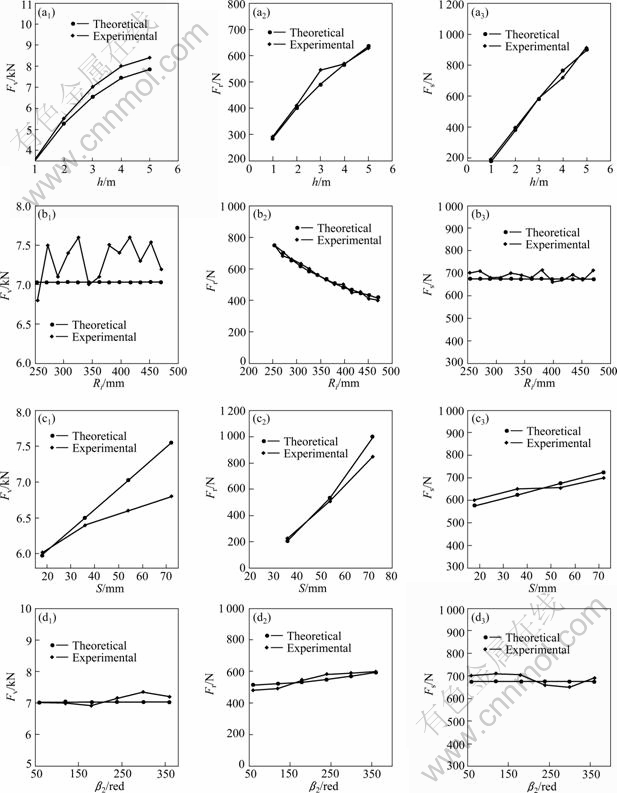
Fig. 7 Comparison between experimental cutting force and theoretical value in different conditions: (a) Variation of rotary cutting force with cutting depth; (b) Variation of rotary cutting force variation with installation radius; (c) Variation of rotary cutting force variation with cutter space; (d) Variation of rotary cutting force variation with phase difference of one side of disc cutter

5 Characteristics of cutting force of disc cutter

As 17-inch disc cutter is selected and the relevant experimental conditions are not adequate, the related parameters of 17-inch disc cutter are analyzed only through the theory. The corresponding granite parameters of Guangzhou Metro Line and the disc cutter structures and installation parameters are calculated. Because the variation law of the rolling force and the vertical force is consistent with the variation of cutter disc layout parameters, the relationships between vertical force, lateral force and layout parameters of disc cutter are present. The following conclusions can be obtained from Fig. 8.

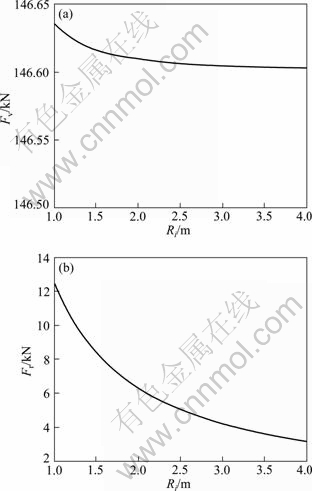
Fig. 8 Variations of vertical force (a) and lateral force (b) with installation radius

1) When several disc cutters carry on rotary cutting, with changing the installation radius and the phase angle between adjacent disc cutters, vertical force and rolling force would remain basically constant, but both forces increase with increasing the cutter space.

2) When several disc cutters carry on rotary cutting, lateral force decreases with increasing installation radius, but increases with increasing cutter space and phase angle between adjacent disc cutters.

3) Under a cutting condition, taking the relative position of disc cutters as an example, with different installation radii, the cutting force of disc cutter varies, as shown in Fig. 7. Compared to the outermost disc cutter, vertical force and rolling force of the innermost disc cutter increase by 0.26%; compared to the outermost disc cutter, the lateral force of the innermost disc cutter increases by 76%.

4) When several disc cutters carry on rotary cutting, with changing the angle between inside and outside of disc cutter, the cutting force varies, as shown in Fig. 9. When the phase angle between one disc cutter and its outboard adjacent disc cutter reaches the maximum of 5π/6, and the cutter and its inboard adjacent disc cutter have no phase difference, the lateral force of disc cutter reaches the maximum. And when the disc cutter has no phase difference with its adjacent inboard and outboard disc cutters, the lateral force of disc cutter reaches the minimum, and the maximum decreases by 17.2% compared to the minimum.

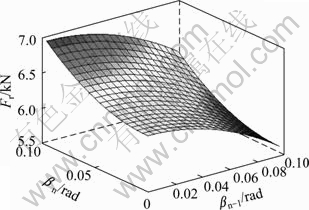
Fig. 9 Variation of cutting force with phase angle

6 Conclusions

1) The flatness of the radial direction on the tunneling interface is related to phase difference between adjacent disc cutters. When the phase difference is larger, the interface is rougher. The volumes of broken rock are different between inside and outside of disc cutter, and if the installation radius of disc cutter is smaller, the difference of the volume is larger.

2) The three-axis force model of disc cutter is established. The theoretical value of three-axis force model is in good agreement with the experimental value, and the maximum error of lateral force is 8.77%, and the maximum error of vertical force is 11.2%.

3) By analyzing the mechanical characteristics of disc cutter, it can be found that vertical force and rolling force basically do not change with the installation radius and angle difference, but the layout parameters of disc cutter have a great influence on lateral force. The lateral force increases with decreasing installation radius of disc cutter, increasing cutter space, and increasing phase angle between adjacent disc cutters. Taking the typical shield cutter as an example, the vertical force and rolling force of innermost disc cutter increase by 0.26% compared to outermost one; while compared to outermost disc cutter, the lateral force of innermost one increases by 76%.

References

[1] SONG Ke-zhi, YUAN Da-jun, WANG Meng-shu. Study review on the interaction between disc cutter and rock [J]. Journal of Rail Way Engineering Society, 2005(6): 66-69. (in Chinese)

[2] SAFFET Y. Utilizing rock mass properties for predicting TBM performance in hard rock condition [J]. Tunnelling and Underground Space Technology, 2008, 23(3): 326-339.

[3] HUO Jun-zhou, SHI Yan-jun, TENG Hong-fei, CHAI Rong-feng, ZHANG Li-hua. Cutter layout design of full-face rock tunnel boring machine (TBM) [J]. Journal of Mechanical Engineering, 2008, 19(15): 1832-1836. (in Chinese)

[4] ZHANG Z X. Technical note estimate of loading rate for a TBM machine based on measured cutter forces [J]. Rock Mechanics and Rock Engineering, 2004, 37(3): 239-248.

[5] MROUEH H, SHAHROUR I. A simplified 3D model for tunnel construction using tunnel boring machines [J]. Tunneling and Underground Space Technology, 2008, 23(1): 38-45.

[6] GERTSCH R., GERTSCH. L, ROSTAMI. J. Disc cutting tests in colorado red granite: Implications for TBM performance prediction [J]. International Journal of Rock Mechanics & Mining Sciences, 2007, 44(2): 238-246.

[7] CIGLA M, OZDEMIR L. Computer modeling for improved production of mechanical excavators [C]// Proceedings of the Annual Meeting of the Society for Mining. Salt Lake City: Metallurgy and Exploration (SME), 2000: 1-12.

[8] ACAROGLU O. A fuzzy logic model to predict specific energy requirement [J]. Tunnel and Underground Space Technology, 2008, 10(6): 10-16.

[9] CHANG S, CHOI S, BAE G. Performance prediction of TBM disc cutting on granitic rock by the linear cutting test [J]. Tunnelling and Underground Space Technology, 2006, 21: 271-279.

[10] ZHANG Zhao-huang, JI Chang-ming. Analytic solution and its usage of arc length of rock breakage point of disc edge on full face rock tunnel boring machine [J]. Journal of Basic Science and Engineering, 2009, 17(2): 265-273. (in Chinese)

[11] ZHANG Hou-mei, WU Xiu-guo, ZENG Wei-hua. Study on tunneling experiment and mathematical model of EPB shield. Chinese [J] Journal of Rock Mechanics and Engineering, 2005, 24(2): 5732-5766. (in Chinese)

[12] WAN Zhi-chang, SHA Ming-yuan, ZHOU Yan-ling. Study on disk cutters for hard rock-Application of TB880E TBM in Qin-ling Tunnel(1) [J]. Modern Tunnelling Technology, 2002, 39(5): l-11. (in Chinese)

[13] CHIKAOSA T, SHUNICHIRO Y, KIMIKAZU T. A study on cutter wear and mechanical properties of rocks in tunneling with a TBM [J]. Journal of the Society of Materials Science, 2006, 55(1): 29-36.

[14] XIA Yi-min, ZHOU Xi-wen, LIU Yu-jiang, WU Dun. Study on cutters layout rules of EPB shield cutter-head [J]. Natural Science Journal of Xiangtan University, 2009, 31(4): 93-96. (in Chinese)

[15] EVANS I, POMERY C D. The strength fracture and workability of coal [M]. London: Pergamon Press, 1966: 55-59.

[16] ROSTAMI J, OZDEMIR L. A new model for performance prediction of hard rock TBMs [C]// Rapid Excavation and Tunneling Conference (RETC) Proceedings. Boston, 1993: 793-809.

[17] ZUO Yu-jun, LI Xi-bing, ZHOU Zi-long. Determination of ejection velocity of rock fragments during rock burst in consideration of damage [J]. Journal of Central South University of Technology, 2005, 12(5): 618-622.

[18] CAO Wen-gui, LI Xiang, ZHAO Heng. Damage constitutive model for strain-softening rock based on normal distribution and its parameter determination [J]. Journal of Central South University of Technology, 2007, 14(5): 719-724.

(Edited by YANG Bing)

Foundation item: Project(2007CB714002) supported by the National Basic Research Program of China; Project(51074180) supported by the National Natural Science Foundation of China; Project(2010FJ1002) supported by Hunan Municipal Science and Technology Program, China

Received date: 2011-04-19; Accepted date: 2012-03-06

Corresponding author: XIA Yi-min, Professor, PhD; Tel: +86-731-88876926; E-mail: xiaymj@csu.edu.cn