J. Cent. South Univ. (2012) 19: 282-286
DOI: 10.1007/s11771-012-1002-9
One-dimensional consolidation of
visco-elastic aquitard due to withdrawal of deep-groundwater
LIU Jia-cai(刘加才)1, LEI Guo-gang(雷国刚)2, MEI Guo-xiong(梅国雄)1
1. College of Transportation Science and Engineering, Nanjing University of Technology, Nanjing 210009, China;
2. Nanjing Water Conservancy Construction Corporation, Nanjing 210036, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: One-dimensional consolidation of visco-elastic aquitard due to withdrawal of deep-groundwater was studied. Merchant model was used to simulate visco-elastic characteristic of aquitard. General solutions of the governing equation were obtained by applying Laplace transform with respect to time, and then the pore-pressure, strain and deformation of the aquitard could be calculated by Laplace inversion. A case was analyzed to validate the correctness of the present method. Finally, some consolidation properties of the problem were analyzed. Comparison of the average degree of consolidation defined by pore pressure with that defined by settlement shows that they are different and the maximum difference is 22.8%. The influences of parameters of Merchant model and the rate of the water level on the consolidation are great. The smaller the viscosity coefficient is, the later the rate of consolidation decreases. The rate of consolidation is decreased with the decrease of the rate of the water level fall. Therefore, the lagged effect of land subsidence should be considered in the actual project.
Key words: consolidation; withdrawal of deep-groundwater; visco-elastic characteristic; Laplace inversion
1 Introduction
Land subsidence is a kind of widespread geological disaster that occurs in many countries and regions all over the world [1-7]. In China, land subsidence mainly occurs in 17 provinces in the eastern and middle regions, including Shanghai, Tianjin, Jiangsu and Hebei provinces [8]. The subsidence is resulted from the heavy withdrawal of ground water, geothermal fluids, oil and gas; the extraction of coal, sulphur and other solids through mining; the hydro-compaction of sediments; oxidation and shrinkage of organic deposits; the catastrophic development of sinkholes in karst terrain, and other phenomena. Land subsidence is mainly caused by widespread water reservoir overexploitation. It is shown that a key to evaluation of land subsidence is correct evaluation of the behavior of aquitards [9-10]. That is why most previous researches on land subsidence are focused on the soil deformation features of shallow soft sediments. Several land subsidence models built for analysis assume that the compressibility of the sand layer is purely elastic and the behavior of clayey layers obeys Terzaghi’s one-dimensional consolidation theory [11-14]. Some researches showed that the soft clay had creep behavior that should be considered in the calculation of land subsidence [15-16]. The Merchant rheological model was widely used for soil consolidation analysis [17]. Its main advantage is that it represents some essential features of consolidating soil, while requiring a minimal number of parameters.
In this work, land subsidence that may be resulted from consolidation of visco-elastic aquitard overlying aquifer caused by reductions in piezometric head in an aquifer is described. Merchant rheological model is used to simulate the stress-strain relationship of the clay. The analytical solutions are obtained by Laplace transform. The pore pressure, strain and deformation of the clay can be calculated by Laplace inversion. The present method is coded into a program. A case is analyzed to validate the correctness of the present method. In addition, according to numerical examples, the influence of parameters of Merchant model and the rate of water level fall on the consolidation is investigated.
2 Mathematical model
The system consists of a non-confined and a confined aquifer separated by an aquitard, as shown schematically in Fig. 1. Each layer is homogeneous. The flow in the aquitard follows Darcy’s law. The vertical coefficient of permeability is kv. Merchant rheological model is adopted to simulate the visco-elastic characteristics of the clay aquitard. This model includes an independent spring of modulus E0, a Kelvin body with a spring of modulus E1, and a dashpot of viscosity coefficient h1. The thickness of the clay aquitard is H. The initial heads of the bottom and the top of the aquitard are equivalent at elevation h above the top of the confined aquifer. The non-confined aquifer is not pumped and its water level remains unchanged. The confined aquifer is pumped and drawdown of the water lever with time can be described as Dh(t).
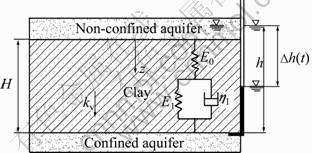
Fig. 1 Illustration of consolidation problem
The equation governing consolidation of the aquitard clay layer is given by
(1)
where εz is the vertical strain; u is the total pore water pressure, including excess pore water pressure and static pore water pressure; gw is the unit weight of water; t and z are time and depth, respectively.
Based on the Merchant rheological model, the vertical strain of the soil mass εz can be expressed in an integral form as
(2)
where d is the flexibility coefficient of the Merchant rheological model, and is given by
(3)
By substituting Equation (3) into Equation (2), and substituting Equation (2) into Equation (1), the governing equation can be expressed in the following form:
(4)
The boundary conditions can be written as follows:
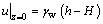(5a)
(5b)
The initial conditions can be written as follows:
(6)
3 Solutions and validation
3.1 Solutions
If u*=u-u(z, 0), Equation (4) can be changed to Equation (7) by applying Laplace transform with respect to time:
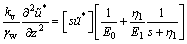(7)
where 
is the Laplace transformation of 
,
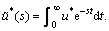
General solution of Equation (7) can be written as follows:
(8)
where 
; 
; A1 and A2 are undetermined coefficients.
The corresponding boundary conditions of Equation (5) can be expressed as the following equations by applying Laplace transform with respect to time:
(9a)
(9b)
where 
is the Laplace transformation of Δh(t),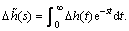 
By substituting Equation (8) into Equation (9), the following equations can be obtained:
(10a)
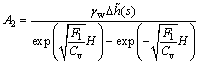(10b)
By substituting Equation (10) into Equation (8),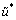 
can be obtained. By inverting the results, the pore pressure solutions of the problem can be obtained as follows:
(11)
in the frequency domain can be obtained according to the following equation changed from Equation (2):
(12)
ε(z,t) can be obtained by inverting such solution into the time domain:
(13)
The total settlement can be written as
(14)
It is difficult to obtain an analytical solution for the inverse Laplace transform given by the above equations. Many numerical inversion techniques can be used to achieve an approximate solution by inverting the function from Laplace space to the time domain [18-22]. The De Hoog algorithm employs the Fourier series in the polynomial approximation of the Laplace inverse and achieves more accurate results by accelerating the convergence of the Fourier series. The De Hoog algorithm is used to numerically invert the frequency domain solutions.
3.2 Validation
If Δh(t)=H , the analytical solution of the pore pressure can be obtained as follows:
(15)
where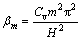 
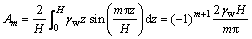
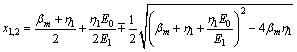
If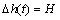 
, 
, A1 and A2 can be determined through Equation (10), and 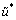can be obtained through Equation (8). So, pore pressure solutions of the problem u(z, t) can be determined by inverting the results through Equation (11).
In order to illustrate the effectiveness of the solving method and the correctness of programming, a case is analyzed by analytical solution and the present solving method, respectively, and the solutions are compared.
Figure 2 shows the comparison of pore pressures obtained from analytical and present solutions, where h=12 m, Dh(t)=H=10 m, E0=2 MPa, E1=5 MPa, h1= 1.0×10-8 s-1, kv=1.0×10-8 m/s. As can bee seen, the results obtained from the present method match well with the analytical ones.
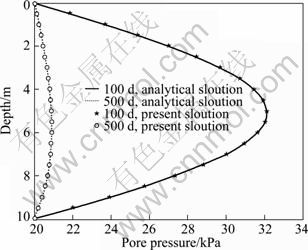
Fig. 2 Comparison of pore pressures obtained from analytical and present solutions
4 Discussion
4.1 Comparison of average degree of consolidation defined by pore pressure and by settlement
Once the expression for the pore pressure is known, the average degree of consolidation defined by pore pressure can be obtained from the following equation:
(16)
The average degree of consolidation can also be defined by settlement, which can be obtained from the following equation:
(17)
Recursive adaptive Lobatto quadrature is used to approximate the integral of the function of variable z from 0 to H within an error of 1.0×10-6.
The comparisons of Up and Us of the above case are shown in Figure 3. It can be clearly seen that the overall average degree of consolidation defined by the pore pressure is different from that defined by the settlement. The value of the overall average degree of consolidation defined by the pore pressure is larger than that defined by the settlement at the same time. Difference between the average consolidation degree defined by the two methods is the largest at 158.5 d, which reaches 22.8%. However, the difference disappears gradually with the increase in time t.
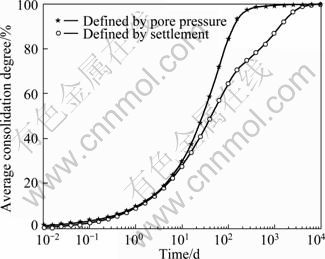
Fig. 3 Comparison of overall average degree of consolidation
4.2 Visco-elastic influence on consolidation process
The visco-elastic characteristic of the clay is mainly controlled by the viscosity coefficient h1 of the dashpot and its value is usually in the range of 1.0×10-8-1.0×10-6 s-1. If h1→?, the aquitard Merchant rheological model degenerates into an equivalent independent spring of
modulus Ee, where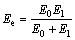 
.
Figure 4 shows the influence of h1, where other parameters remain the same as the above example, and h1 varies from 1.0×10-8 to 1.0×106 s-1. The overall average degree of consolidation defined by the settlement is used here because settlement is more considered in practical engineering. h1=1.0×106 s-1 can be thought approximatively as h1→?. As can be seen from Fig. 4, with the decrease of h1, the rate of consolidation is decreased and the rheological behavior becomes more and more obvious. It can be seen that the smaller the viscosity coefficient h1, the larger the difference of the overall average degree of consolidation, and the later the time.
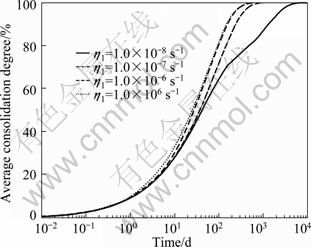
Fig. 4 Influence of h1 on consolidation process
4.3 Influence of water level fall rate on consolidation process
Actually, water level fall caused by withdrawal of ground water does not happen instantaneously. Water level fall usually can be described as exponential function, such as 
at the above example, where parameter b is used to reflect the speed of water level fall with unit of d-1. If b→?, the water level fall happens instantaneously. b=10 000 d-1 can be thought approximatively as b→? .
Figure 5 shows the influence of b, where h1=1.0×10-8 s-1 and other parameters remain the same as the above example. The overall average degree of consolidation defined by the settlement is still used here. As can be seen from Fig. 5, with the decrease of b, the rate of consolidation is decreased. It can be seen that the consolidation of the visco-elastic clay hardly happens during pumping. The longer the time spent for same water level fall, the later the land subsidence happens.
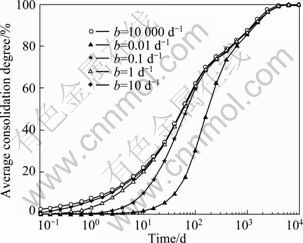
Fig. 5 Influence of parameter b on consolidation process
5 Conclusions
1) A model is presented to describe land subsidence resulted from consolidation of visco-elastic aquitard overlying aquifer caused by reductions in piezometric head in an aquifer. The analytical solutions are obtained by Laplace transform. The pore-pressure, strain and deformation of the aquitard can be calculated by Laplace inversion. A case is analyzed by analytical solution and the present solving method, respectively. The results obtained from the present method match well with the analytical one, which validates the correctness of the present method.
2) The overall average consolidation degree defined by the pore pressure is different from that defined by the total settlement. The overall average degree of consolidation defined by the total settlement is smaller than the value defined by the pore pressure. The maximum difference is 22.8%. Therefore, the land subsidence obviously lags behind pore pressure disappearing.
3) The viscosity coefficient of the dashpot has great influence on the consolidation process. The rate of consolidation is decreased with the decrease of coefficient. The smaller the viscosity coefficient is, the later the rate of consolidation decreases.
4) The magnitude of the water level fall and the time spent for same water level fall have also great influence on the consolidation process. The rate of consolidation is decreased with the decrease of the rate of the water level fall.
References
[1] PHIEN-WEJ N, GIAO P H, NUTALAYA P. Land subsidence in Bangkok, Thailand [J]. Engineering Geology, 2006, 82(4): 187-201.
[2] YI Li-xin, WANG Jie, SHAO Chuan-qing. Land subsidence disaster survey and its economic loss assessment in Tianjin, China [J]. Natural Hazards Review, 2010, 11(1): 35-41.
[3] STIROS S C. Subsidence of the Thessaloniki (northern Greece) coastal plain, 1960–1999 [J]. Engineering Geology, 2001, 61(4): 243-256.
[4] SHEN S L, TOHNO I, NISHIGAKI M, MIURA N. Land subsidence due to withdrawal of deep-groundwater [J]. Lowland Technology International, 2004, 6(1): 1-8.
[5] LEWIS R R, SCHREFLER B. A fully coupled consolidation model of the subsidence of Venice [J]. Water Resources Research, 1978, 14(2): 223-230.
[6] YANG X L, ZOU J F. Cavity expansion analysis with non-linear failure criterion [J]. Proceedings of the Institution of Civil Engineers-Geotechnical Engineering, 2011, 164(1): 41-49.
[7] YANG X L, YIN J H. Slope stability analysis with nonlinear failure criterion [J]. Journal of Engineering Mechanics, 2004, 130(3): 267–273.
[8] XUE Y Q, ZHANG Y, YE S J. Land subsidence in China [J]. Environmental Geology, 2005, 48(6): 713–720.
[9] HELM D C. One-dimensional simulation of aquifer system compaction near Pixley, California. 2: Stress-dependent parameters [J]. Water Resources Research, 1976, 12(3): 375-391.
[10] GAMBOLATI G, FREEZE R A. Mathematical simulation of the subsidence of Venice. 1. Theory [J]. Water Resources Research, 1973, 9(3): 721–733.
[11] QIAN Shou-yi, GU Xiao-yun. Calculation of land subsidence in Shanghai [J]. Chinese Journal of Geotechnical Engineering, 1981, 3(3): 1-9. (in Chinese)
[12] LI Qin-fen, FANG Zheng, WANG Han-mei. Calculation and prediction of model of extractive groundwater in Shanghai [J]. Shanghai Geology, 2000, 13(2): 36-43. (in Chinese)
[13] HU R L, WANG S J, LEE C F. Characteristics and trends of land subsidence in Tanggu, Tianjin, China[J]. Bulletin of Engineering Geology and the Environment, 2002, 61(3): 213–225.
[14] ZHANG Yun. One-dimensional model for land subsidence and its solution [J]. Journal of Engineering Geology, 2002, 10(4): 434–437. (in Chinese)
[15] MEN Fu-lu. Preliminary investigations on rheological properties of clay and ground settlement in Shanghai city (I) [J]. Journal of Natural Disasters, 1999, 8(3): 117–126. (in Chinese)
[16] MEN Fu-lu. Preliminary investigations on rheological properties of clay and ground settlement in Shanghai city (II) [J]. Journal of Natural Disasters, 1999, 8(4): 123-132. (in Chinese)
[17] LIU Jia-cai, ZHAO Wei-bing; ZAI Jin-min, WANG Xu-dong. Analysis of one-dimensional consolidation of double-layered viscoelastic ground [J]. Rock and Soil Mechanics, 2007, 28(4): 743–746, 752. (in Chinese)
[18] STEHFEST H. Numerical inversion of Laplace transforms [J]. Communications of the ACM, 1970, 13(1): 47–49.
[19] YANG Xiao-li, HUANG Fu. Slope stability analysis considering joined influences of nonlinearity and dilation [J]. Journal of Central South University of Technology, 2009, 16(2): 292–296.
[20] YANG Xiao-li, HUANG Fu. Influences of strain softening and seepage on elastic and plastic solutions of circular openings in nonlinear rock masses [J]. Journal of Central South University of Technology, 2010, 17(3): 621–627.
[21] DURBIN F. Numerical inversion of laplace transforms: An efficient improvement to Dubner and Abate’s method [J]. Computer Journal, 1974, 17(4): 371–376.
[22] de HOOG F R, KNIGHT J H, STOKES A N. An improved method for numerical inversion of Laplace transforms [J]. Society for Industrial and Applied Mathematics, 1982, 3(3): 357–366.
(Edited by YANG Bing)
Foundation item: Project(50608038/E0806) supported by the National Natural Science Foundation of China
Received date: 2010-11-18; Accepted date: 2011-07-05
Corresponding author: LIU Jia-cai, Associate Professor, PhD; Tel: +86-25-83239749; E-mail: liujchhu@163.com
