Trans. Nonferrous Met. Soc. China 23(2013) 1269-1274
Optimization of process parameters for in situ casting of Al/TiB2 composites through response surface methodology
K. NIRANJAN, P. R. LAKSHMINARAYANAN
Department of Manufacturing Engineering, Annamalai University, Annamalai Nagar-608 002, Tamilnadu, India
Received 12 March 2012; accepted 28 February 2013
Abstract: The mathematical models were developed to predict the ultimate tensile strength (UTS) and hardness of Al/TiB2 MMCs fabricated by in situ reaction process. The process parameters include temperature, reaction time and mass fraction of TiB2. The in-situ casting was carried out based on three-factor five-level central composite rotatable design using response surface methodology (RSM). The validation of the model was carried out using ANOVA. The mathematical models developed for the mechanical properties were predicted at 95% confidence limit.
Key words: in situ casting; metal matrix composites; TiB2 reinforcement; response surface methodology
1 Introduction
Metal matrix composites (MMCs) have emerged as an important class of materials for structural, wear, thermal, electrical, automobile and aeronautical applications, primarily as a result of their ability to exhibit superior specific strength when compared to other commercial alloys. The MMCs are synthesized in numerous manners with respect to the requirements and application. The composites processed using the conventional methods suffer, in common, from matrix reinforcement interfacial thermodynamics instability, thus limiting their ambient and high temperature mechanical properties. In order to overcome this limitation and to ensure good matrix to reinforcement compatibility, microstructural homogeneity efforts have been made to synthesize and fabricate the MMC in a single stage from its raw materials. In situ process represents one such category of technique used to synthesize MMC [1]. In-situ MMCs reinforced by ceramic particulates have attracted considerable interest due to their advantages, such as well distributed fine reinforcements and good bonding with the matrix, and a clean reinforcement/matrix interface. Most of the studies reported are related to the fabrication and the mechanical properties of silicon carbide or alumina reinforced aluminum alloy composites [2]. YUE et al [3] established thermodynamic model describing the formation of in-situ TiB2 reinforced Al MMCs. Based on the thermodynamic principles, the Gibbs free energy of formation of TiB2 was evaluated. MALLIKARJUNA and SHASHIDHARA [4] done their research on aluminum alloy 2014–TiB2. The MMC was fabricated by an exothermic reaction process at 850 °C using K2TiF6 and KBF4 halide salts. SEM observation revealed the hexagonal shape of the in-situ TiB2 particles. Exothermic reaction was completed with the increase in reaction time, but the size of the in-situ TiB2 particles was less depending on the reaction time. In exothermic reaction the mass fraction of TiB2 increased with reduction in the grain size. These resulted in the increase in yield strength, ultimate tensile strength and microhardness of the composite. CHRISTY et al [5] reported that the TiB2 formation greatly improved the properties of Al 6061 alloy. The mechanical properties are greatly improved for Al6061-12%TiB2 as compared with Al 6061 alloy.
Information related to the synthesis of composites with in situ TiB2 reinforcement is, however, very limited. The present investigation, therefore, emphasizes the features of the development of comprehensive mathematical models for correlating the interactive and higher order influences of the various predominant process parameters on ultimate tensile strength (UTS) and hardness of MMCs fabricated by in situ casting technique. The investigation into the influence of in situ casting process parameters is carried out through response surface methodology (RSM) utilizing the relevant experimental data obtained through experiments. The adequacy of the developed mathematical model is also tested by the analysis of variance test (ANOVA). An attempt is made to obtain optimal process parameters for maximum UTS and hardness of the composites fabricated by in-situ technique.
2 Experimental
For the fabrication of MMC, aluminum alloy A356 was used as the base metal. Two kinds of salts, namely K2TiF6 and KBF4, were used to synthesize the TiB2 reinforcement. Al/TiB2 composite was produced using five different levels of the following three factors: 1) Temperature (800 °C to 1000 °C); 2) Reaction time (20 min to 40 min); 3) Mass fraction of TiB2 (2% to 6%).
Aluminum alloy was melted at the required temperature, then two kinds of salts were added and stirred in the molten aluminum. The experiment was conducted in the stir casting furnace.
The stirrer used was mild steel to avoid possible contamination of the molten metal. Chemical reactions between the two salts and molten aluminum alloy took place to form in situ TiB2 particulates in aluminum alloy. The period of chemical reaction was varied in five levels of 20, 25, 30, 35 and 40 min to investigate the relationship between the degree of reaction and the growth behavior of TiB2.
The reactions were summarized as
3Al+2Ti+2B→TiB2+Al3Ti (1)
Ti+2B→TiB2 (2)
Ti+3Al→Al3Ti (3)
At the end of this reaction, the MMC product was cast into rods of 35 mm in diameter [6]. The specimens were made from the cast rods according to ASTM standard E 8M [7]. Tensile tests were carried out at room temperature at a constant displacement rate on a UNITEK-94100 UTM machine. Microhardness values of the composite were gotten using Vickers micro hardness tester.
3 Mathematical model development
In order to find out the relationship between the process parameters and the mechanical properties, second order polynomial response surface mathematical models can be considered as [8,9]
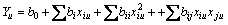 (4)
(4)
where Yu is the corresponding response; xiu is the coded values of the i-th casting parameters for u-th experiments; and bi, bii, bij are the second order regression coefficients. The second term under the summation sign of this polynomial equation is attributable to linear effect, while the third term corresponds to the higher order effect. The fourth term of the equation includes the interactive effects of the process parameters.
Owing to wide ranges of the factors about the in situ process, it was decided to use three factors with five levels, and central composite rotatable design matrix was chosen to optimize the experimental conditions. The main objective of the factorial experiments consisted of studying the relationship between the response as a dependent variable and the parameter levels. This approach helps to understand how the change in the levels of parameters affects the response. The combination of the levels of the parameters leads to certain optimum response.
The present investigation studied the effects of factors like: 1) Casting temperature (X1); 2) Reaction time (X2); 3) Mass fraction of TiB2 (X3).
The response parameters are ultimate tensile strength (UTS), and hardness of the fabricated Al/TiB2 MMCs. A 2k factorial with central composite second order design was used (in this case k=3). This consists of 2k=6 axial points at γ= ±1.682 and a centre point at zero level repeated seven times n0 to estimate the error.
The coded and actual values of the parameters used in the present work are listed in Table 1. 20 experiments were conducted and the values (response) of UTS and hardness along with the design matrix are tabulated in Table 2. For analyzing the data, the fitness of the model is very much required. Checking accuracy of the models included test for significance of the regression model, test for significance on model coefficient and test for lack of fit. For this purpose, analysis of variance (ANOVA) was performed.
Table 1 Experimental parameter and levels

Table 2 Experimental plan and result based on central composite second order rotatable design
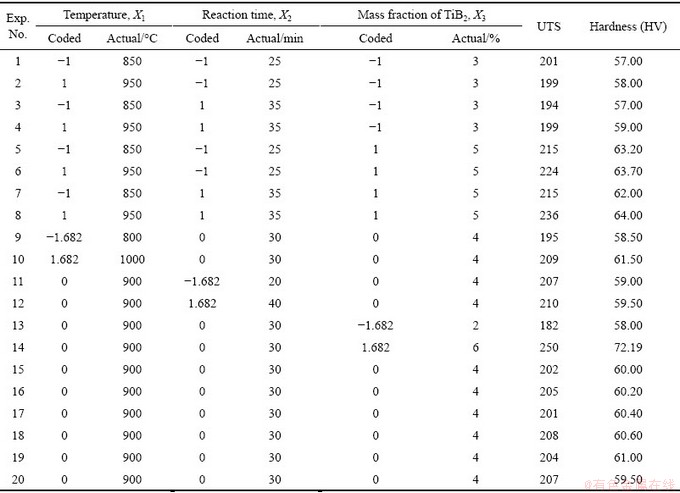
Table 3 Test for significance of UTS
3.1 Mathematical model for ultimate tensile strength (UTS)
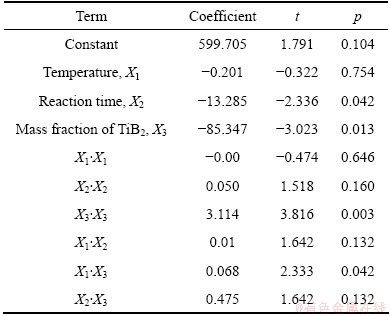
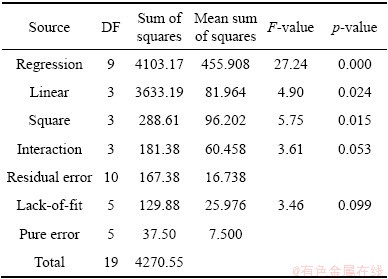
The test of significance of UTS was carried out using the quadratic model. The results of the quadratic model for UTS are given in Table 3. The values of R2 and adjusted R2 are 96.08% and 92.55%. This means that the regression model provides a complete relationship between the dependent and independent variables. The associated p value for the model is <0.05 (i.e., α=0.05 or 95% confidence), indicating that the model is considered to be statistically significant. The standard F value for 95% confidence limit is 5.05. As shown in Table 4, the F value of 3.46 for lack of fit is smaller than the standard value. Hence the model is adequate. It is also seen that from the p values, the main effect X2, X3 and second order effect X3 is significant. The other model terms can be regarded not significant due to their probability values being more than 0.05. Figure 1 displays the normal probability of residuals for UTS. It is observed that the residuals are distributed normally and in a straight line and hence the model is adequate.
Table 4 Test result of ANOVA for UTS
Using the results presented in Table 3, the derived model is shown as:
σb=599.705-0.201X1-13.285X2-85.347X3-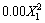 +
+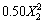 +
+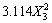 +0.01X1·X2+0.068X1·X3+0.475X2·X3 (5)
+0.01X1·X2+0.068X1·X3+0.475X2·X3 (5)
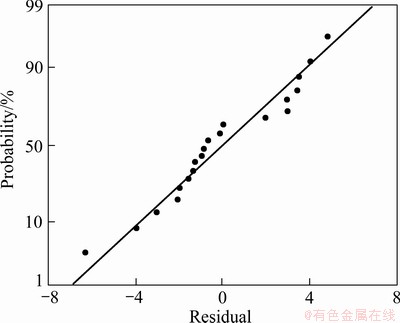
Fig. 1 Normal probability plot for UTS
3.2 Mathematical model for hardness
The test of significance of hardness was carried out using the quadratic model and statistically significant analysis. The results of the quadratic model for hardness are given in Table 5.
Table 5 Test for significance of hardness
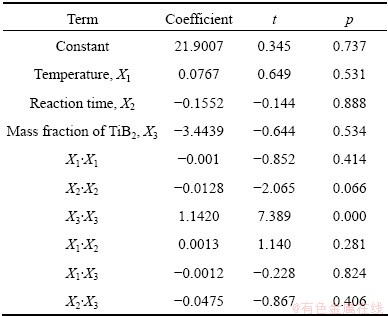
The value of R2 and adjusted R2 are 97.23% and 94.74%. This means that the regression model provides a complete relationship between the dependent and independent variables. The associated p value for the model is <0.05 (i.e., α=0.05 or 95% confidence), indicating that the model is considered to be statistically significant. The standard F value for 95% confidence limit is 5.05. As shown in Table 6, the F value (3.52) for lack of fit is smaller than the standard value. Thus the model is adequate. It is also seen that from the p values the second order effect X2 and X3 are significant. The other model terms can be regarded not significant as their probability values are greater than 0.05 in the F test. Figure 2 displays the normal probability of residuals for hardness. It is observed that the residuals are distributed normally and in a straight line and hence the model is adequate. Based on the results presented in Table 5, the form of the derived model is shown as
H=21.900+0.076X1-0.1552X2-3.44X3- -
- +
+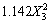 +0.0013X1·X2-0.0012X1·X3-0.0475X2·X3 (6)
+0.0013X1·X2-0.0012X1·X3-0.0475X2·X3 (6)
The adequacy of the above models was also tested through the analysis of variance (ANOVA). The results of the analysis justifying the closeness of fit of the mathematical model were enumerated, as shown in Table 4 and 6. It was concluded that the evolved models given by Eqs. (5) and (6) are quite adequate at 95% confidence level.
Table 6 Test result of ANOVA for hardness
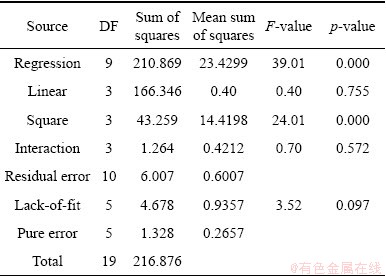
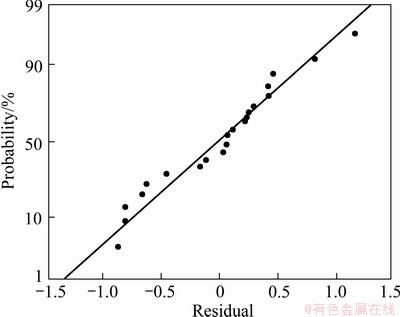
Fig. 2 Normal probability plot for hardness
4 Results and discussion
The effect of reaction time and temperature on UTS is shown in Fig. 3. It is seen that as reaction time and melt temperature increase beyond 900 °C, UTS increases nonlinearly. At a lower temperature less than 900 °C, UTS decreases because matrix and reinforcement can offer more space for the transfer of dislocations with respect to increasing reaction time.
The response surface plot of UTS with respect to reaction time and mass fraction of TiB2 is shown in Fig. 4. The UTS increases with the increase in mass fraction of TiB2 for all values of reaction time.
The effect of temperature and reaction time on hardness is shown in Fig. 5 Hardness increases with the increase of temperature for all level of reaction time. As the melt temperature increases, the hardness also increases.
Figure 6 depicts the effect of reaction time and mass fraction of TiB2 on hardness. Hardness increases with the increase in mass fraction of TiB2 for all values of reaction time. This is due to the fact that the reinforcement acts as barrier during the migration of dislocation and also grain refining. Reaction time has the same effect on hardness as seen earlier and has little effect on hardness as compared to the effect of mass fraction of TiB2.
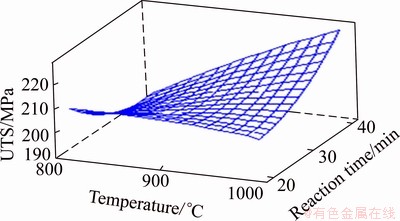
Fig. 3 Influence of temperature and reaction time on UTS of specimen with 4% TiB2
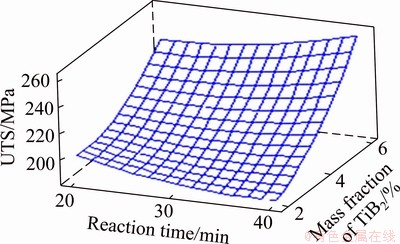
Fig. 4 Influence of reaction time and mass fraction of TiB2 on UTS of specimen at temperature of 900 °C
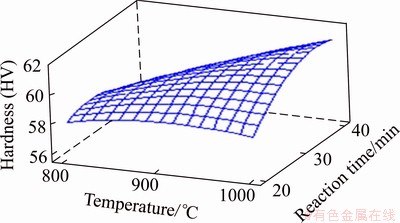
Fig. 5 Influence of temperature and reaction time on hardness of specimen with 4% TiB2
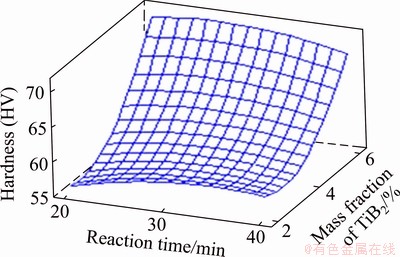
Fig. 6 Influence of reaction time and mass fraction of TiB2 on hardness of specimen at temperature of 900 °C
5 Optimization
Based on the developed second order response surface equations correlating the various casting process parameters with the UTS and hardness values, optimality search was done. An analysis for the optimization of process parameter was carried out using response surface methodology (RSM) optimization technique [10]. The goal was to maximize the UTS and the hardness, at a specific combination of input factors being considered. The optimum values of the input process parameters for in situ MMC fabrication process are temperature 949.18 °C; reaction time 33.64 min and mass fraction of TiB2 5.96%.
For in situ casting with optimum parametric combination, UTS can be achieved as high as 261.84 MPa and the hardness can be achieved as high as HV 70.98.
6 Conclusions
Al-TiB2 composite was successfully manufactured by in situ salt reaction technique. Mathematical models have been developed based on RSM approach.
The developed RSM based mathematical modeling has the potential to evaluate UTS and hardness under various process parameter settings. The adequacy of the developed mathematical model was also tested through the analysis of variance (ANOVA). The results of the analysis justify the closeness of fit of the mathematical model at 95% confidence level.
The influence of different process parameters on in situ casting technique was exhibited though surface plots. It is clear from the response surface plot of UTS that, the UTS increases with the increase in mass fraction of TiB2. And the hardness increases with increase in mass fraction of TiB2.
From the developed models the optimal input factor combination for Al/TiB2 composite was found as temperature 949.18 °C, reaction time 33.64 min and mass fraction of TiB2 5.96%. The maximum UTS and hardness are 261.84 MPa and HV 70.98, respectively.
References
[1] CARACOSTAS C A. Tribological properties of aluminum alloy matrix TiB2 composite prepared by in-situ processing [J]. Metallurgical and Materials Transactions A, 1997: 491-502.
[2] LAKSHMI S, LU L, GUPTHA M. In situ preparation of TiB2 reinforced Al based composites [J]. Journal of Materials Processing Technology, 1998, 73: 160-166.
[3] YUE N L, LU L, LAI M O. Application of thermodynamic calculation in the in-situ process of Al/TiB2 [J]. Composite Structures, 1999, 47: 691-694.
[4] MALLIKARJUNA C, SHASHIDHARA S M. The precipitation of TiB2 in aluminum alloy melts from the exothermic reaction of K2TiF6 and KBF4 halide salts and evaluation of its mechanical properties [C]//World Congress on Engineering and Computer Science. San Francisco, USA, 2007: 978-988.
[5] CHRISTY T V, MURUGAN N, KUMAR S. A comparative study on the microstructures and mechanical properties of Al 6061 alloy and the MMC Al 6061/TiB2/12p [J]. Journal of Minerals & Materials Characterization & Engineering, 2010, 9(1): 57-65.
[6] TEE K L, LU L, LAI M O. Improvement in mechanical properties of in-situ Al-TiB2 composite by incorporation of carbon [J]. Materials Science and Engineering A, 2003, 325: 227-231.
[7] SURAPPA M K. Aluminum matrix composites: Challenge and opportunities [C]//Sadhana-Academy Proceedings in Engineering Sciences. www. springerlink. Com, 2003, 28: 319-334.
[8] FENG C F, FROYEN L. Microstructure of in-situ Al/TiB2 MMCs prepared by a casting route [J]. Journal of Material sciences, 2000, 35: 837-850.
[9] PALANIVEL R, KOSHY MATHEWS P, MURUGAN N. Development of mathematical model to predict the mechanical properties of friction stir welded AA6351 aluminum alloy [J]. Journal of Engineering Science and Technology Review, 2011, 4: 25-31.
[10] MOLDOVAN P, BUTTU M, CIUC I, DRAGUT V. On the mechanism and thermodynamics of the perception of TiB2 particles in 6063 Matrix aluminum alloy [J]. U.P.B. Science Bulletin, Series B, 2011, 73: 205-216.
采用响应面方法对原位反应铸造制备Al/TiB2金属基复合材料工艺参数进行优化
K. NIRANJAN, P. R. LAKSHMINARAYANAN
Department of Manufacturing Engineering, Annamalai University, Annamalai Nagar -608 002, Tamilnadu, India
摘 要:开发了数学模型来预测原位反应生成的Al/TiB2金属基复合材料的最大拉伸强度和硬度。考察的工艺参数包括反应温度、反应时间和TiB2添加量。采用响应面方法,基于3因素5水平的中心复合旋转来设计原位反应实验方案。对所得模型采用ANOVA方法进行了验证。表明所得的模型对制备的材料力学性能的预测可信度在 95%以上。
关键词:原位反应铸造;金属基复合材料;TiB2增强体;响应面方法
(Edited by Sai-qian YUAN)
Corresponding author: K. NIRANJAN; Tel: +91-9842640188; E-mail: niranj1974@gmail.com
DOI: 10.1016/S1003-6326(13)62592-3