Volume sequences of characteristic atoms separated from

experimental volumes of AuCu and AuCu3 compounds

XIE You-qing(谢佑卿)^{1, 2, 3}, LIU Xin-bi(刘心笔)¹, LI Xiao-bo(李晓波)⁴,

PENG Hong-jian(彭红建)¹, NIE Yao-zhuang(聂耀庄)¹

1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;

2. Powder Metallurgy Research Institute, Central South University, Changsha 410083, China;

 3. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China;

4. College of Mechanical Engineering, Xiangtan University, Xiangtan 411105, China

Received 10 August 2009; accepted 15 September 2009

                                                                                                

Abstract: The systematic science of alloys (SSA) is a framework of the total energy and total volume able to be separated. The volume sequences of characteristic atoms at the central sites of the basic clusters in the fcc-based Au-Cu system are separated out from the experimental volumes of L1₀-AuCu and L1₂-AuCu₃ compounds at room temperature only, by nine volume V-functions. From these volume sequences, the volumes, volumes of formation, ordering (excess) volumes and volume mismatch degrees of the L1₀-AuCu, L1₂-AuCu₃ and L1₂-Au₃Cu compounds, Au₃Cu-, AuCu- and AuCu₃-type ordered alloys with maximal ordering degree, and disordered Au_1-xCu_x alloys are calculated. Among these functions, only ordering volumes of the compounds and ordered alloys obtained by the 6th V-function are negative, i.e., the destruction of the superlattice is accompanied by an increase in volume, which is identical with the experimental results. Accompanying conclusions, the different descriptions of volumetric properties between traditional alloy theories and SSA framework are discussed.

Key words: systematic science of alloys; Au-Cu system; atomic volume; volume of formation; ordering volume; volume mismatch

                                                                                                           

1 Introduction

In order to get an entire understanding of the alloy systems, to establish phase diagrams and to search a method for designing of alloys, the SSA framework[1] has been established on the basis of two scientific philosophy propositions. A diversity of structures, properties and features of whether matter or nonmatter systems should be attributed to combination and arrangement of structural units in the structural unit sequence; and a systematic theory of any complex system described quantitatively should be constructed by structural unit sequence-, equation- and information- chains. The SSA framework is constructed indeed by the structural unit sequence-, equation- and information- chains.

 

1.1 Models and structure unit sequence-chain

An alloy system contains three structure levels: the

phase level of organizations, atomic level of phases and electronic level of atoms. The atomic level of alloy phases in the SSA framework involves three models for constructing diversity of structures and properties of alloy phases[1-4].

1) The basic cluster overlapping (BCO) model, of which the structural units are a pair of basic cluster sequences in a based lattice (such as fcc, hcp and bcc) of binary alloy systems, and each cluster consists of a central atom, the first neighbor configuration, the second neighbor configuration and the third neighbor configuration. The actions of the BCO model are as follows: to give information about an atomic arrangement of alloy phases described by overlapping pattern of basic clusters; and to determine the splitting order on the potential energy, volume and electronic structure of the central atoms, which may have one, two and three splitting orders, respectively, corresponding to the basic clusters with one, two and three neighbor configurations.

 

In the present work, the long-period superlattice structure AuCu Ⅱ is not concerned. Therefore, to use one order split is enough, where the basic -cluster consists of a central  atom and the first neighboring configuration [(I-i)Au, iCu], which contains i Cu-atoms and (I-i) Au-atoms. Here, the symbol α denotes Au or Cu; I is the coordinative number and equals 12 for the fcc- based lattice; i can change from 0 to 12.

2) The characteristic atom arranging (CAA) model, of which the structural units are a pair of characteristic atom sequences, and each characteristic atom is the central atom of a specific basic cluster. The characteristic  atom has own characters at the ground state: potential energy, volume  and electronic structure ψ. The actions of the CAA model are as follows: to give information about an atomic arrangement of alloy phases described by potential energy pattern, volume pattern and electronic structure pattern of the characteristic atoms occupied at the various lattice sites in intermetallics; to derive equations for calculating concentrations of various characteristic atoms and configurational entropy of ordered and disordered alloys as functions of composition (x) and ordering degree (σ); and to establish composition-ordering degree dependent E(x, 0, σ), V(x, 0, σ) and ψ(x, 0, σ) functions of potential energy, volume and electronic structure of alloy phases at 0 K.

Therefore, in a based lattice alloy system the variations in potential energy, volume and electronic structure of intermetallics, various type ordered alloys and disordered alloys with composition and ordering degree can be calculated by the same information about a pair of potential energy sequences, a pair of volume sequences and a pair of electronic structure sequences, which belong to a pair of characteristic atom sequences.

3) The characteristic crystal mixing (CCM) model, of which the structure units are a pair of invented characteristic crystal sequences, and each characteristic crystal consists of the same characteristic atoms with the identical potential energy, identical volume and identical electronic structure. The actions of the CCM model are as follows: to establish a set of temperature (T) dependent functions of the energetic and volumetric properties consisting of general volume V^v(T) function, the general thermal expansion coefficient β(T) function, general vibrational capacity  function, general vibrational energy U^v(T) function, general vibrational entropy S^v(T) function, enthalpy H(T) function and free energy G(T) function of the characteristic crystals; and to derive a set of  composition-temperature-ordering degree dependent functions of the general volume general thermal expansion coefficient general vibration heat capacity general vibrational energy  general vibration entropy enthalpy  and characteristic free energy  without containing configuration entropy  of alloy phases. And finally, combining the  function with partition function the general free energy  function can be derived, where the  function contains configuration entropy  This action will be presented in the future.

These three models are proposed in order to overcome disappointments of the atomic pair interaction model and central atom model[5] as well as effective cluster interaction model[6-9].

 

1.2 Equation- and information-chains

1.2.1 Additive law of q-properties of characteristic crystals (atoms)

According to CCM model (or CAA model), the extensive properties   of a given alloy phase and its components can be obtained by an additive law of the q-properties of characteristic crystals (atoms) (in terms of CCA law or CAA model))[1]:

    (1)

where  and  are the concentrations of the characteristic crystal (atoms).

1.2.2 Nine E(x,0,σ)- and nine V(x,0,σ)- functions of alloy phases at 0 K

In order to make Eq.(1) become a simple, applicable and separable  function (here q denotes E or V), three types of relations of  and  with i have been designed[1, 10-12]:

Type I of straight line relation:

                (2)

Type II of concave parabola relation:

               (3)

Type III of convex parabola relation:

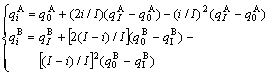   (4)

where  and denote, respectively, corresponding properties of the primary  and  characteristic crystals (atoms);  and  denote, respectively, corresponding properties of the terminal  and  characteristic crystals (atoms).

By combining Eqs.(2), (3), (4) and substituting them into Eq.(1), nine  functions can be obtained, which can be used to compounds, ordered and disordered alloy phases; and nine -functions, which are derived from corresponding  functions and can be used to the disordered alloy phase only[1, 10-13].

 

1.3 Methodology

1.3.1 Inference from the first proposition

The whole can be reproduced from a few parts. For example, the whole of a tree can be reproduced respectively from a seed, a leaf or a branch of the tree, and the whole of a sheep can be reproduced respectively from a egg cell or a body cell of the sheep in biologic systems; the whole information of an alloy system can be reproduced respectively from a few disordered alloys, a few ordered alloys or a few intermetallics. This means that the total potential energies and total volumes of a few alloys can be separated into the potential energy sequence and volume sequence of the characteristic crystals (atoms), from which the whole information about energetic and volumetric properties, electronic and crystalline structures of all alloy phases in an alloy system can be reproduced. Therefore, the systematic study for an alloy system in the SSA framework is divided into three step investigations.

1) The aims of the first step investigation are to choose E(x,0,σ) and V(x,0,σ) functions and to determine a pair of potential energy sequences and a pair of volume sequences of characteristic crystals (atoms), through resolving nine E(x,0,σ)- and V(x,0,σ)-functions on the basis of FP-calculated heats and volumes of formation of a few intermetallics only, or of experimental heats and volumes of formation of a few intermetallics only or a few disordered alloys only by the structural unit inversion method; to determine a pair of electronic structure sequences of characteristic crystals (atoms), according to potential energies and volumes of characteristic crystals (atoms); and finally to study energetic properties, volumetric properties and electronic structures of alloy phases as function of composition (x) at ground state (0 K).

2) The aims of the second step investigation are to obtain energetic and volumetric properties of characteristic crystals as function of temperature, to obtain the energetic and volumetric property equations of alloy phases as functions of composition, temperature and ordering degree and then to study energetic and volumetric properties, crystalline parameters and electronic structures, as well as some physical properties of alloy phases in the whole ranges of composition, temperature and ordering degree.

3) The aims of the third step investigation are to study stability, transformation and equilibrium of alloy phases, to establish phase diagram and to provide a systematic knowledge about energetic and volumetric properties, crystalline and electronic structures of characteristic crystal (atom) sequences for designing applied alloys. That is called as design engineering of characteristic atom sequences of alloy systems.

The potential energy sequences of  and characteristic atoms separated out from experimental heats of formation of some disordered Au_1-xCu_x alloys only[12, 14] and of L1₀-AuCu and L1₂-AuCu₃ compounds only[13, 15] have been performed, respectively. In this work, the volume sequences of the  and characteristic atoms are separated out from experimental volumes of the L1₀-AuCu and L1₂-AuCu₃ compounds.

1.3.2 Survey for descriptions of volumetric properties of alloys in traditional alloy theories

These descriptions are as follows[16-17]: the molar volume, average atomic volume and cell volume of alloys; the volume of formation and change on disordering of intermetallics; the partial atomic volume of components in an alloy, effective atomic volume instead of partial atomic volume and realistic volume instead of partial atomic volume; the volume mismatch of the constituent atoms represented by the ratio of the partial atomic volume of the minor component to that of the elemental volume of the major component.

1.3.3 Volumetric properties of alloys in SSA framework by taking Au-Cu system as an example

1) The volume sequences of characteristic atoms of components Au and Cu represent the realistic volumes of atoms surrounded by various neighbor configurations, and the results are listed in Table 1 and shown in Fig.1.

Table 1 Volume sequences of characteristic atoms calculated by nine V-functions on the basis of experimental volumes of L1₀-AuCu and L1₂-AuCu₃ compounds (in nm³)

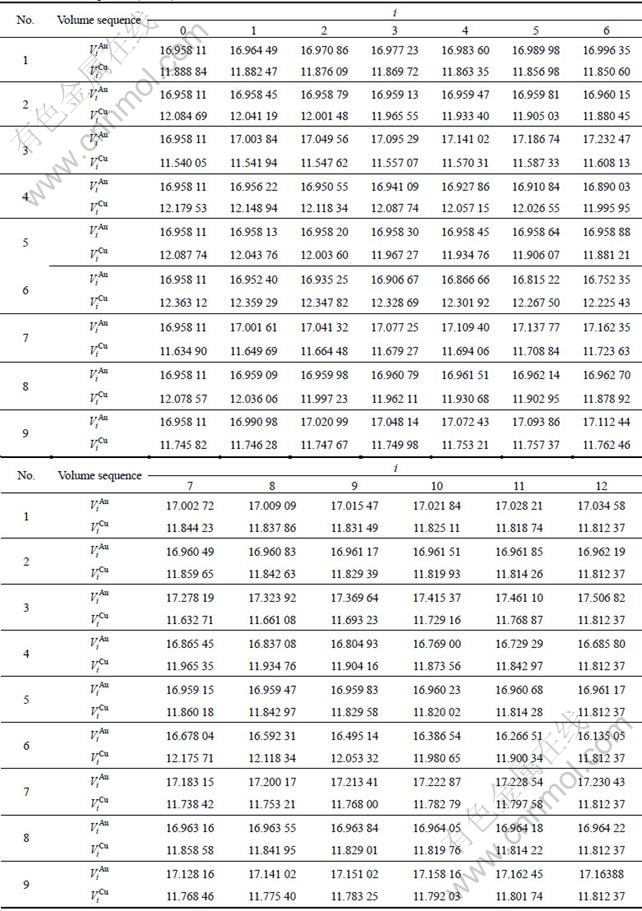
Fig.1 Volume , (a) and lattice parameter ,(b) sequences obtained by the 6th V-function

2) The volumetric properties of disordered and ordered alloys are presented in Section 2.2 and 2.3: the volumes (, ) and concentrations (, ) of characteristic atoms in a given alloy; the average atomic volume V_a(x), average atomic volume of formation average volume V(x) and average volume of formationof a cell for a given alloy; average atomic volume () and average atomic volume (lattice parameter) of formation () of components Au and Cu;     the ordering (excess) atomic volume  which is defined as the difference in average atomic volumes between ordered and disordered alloys.

3) The volumetric properties of L1₀-AuCu, L1₂-AuCu₃ and L1₂-Au₃Cu compounds are presented in Section 2.4: the volumes (,) and numbers (, ) of characteristic atoms in a cell; the total volume V_c and total volume of formation , lattice parameter a and lattice parameter of formation  of a cell; ordering (excess) atomic volume of compounds and ordering lattice parameter average atomic volumes (,), average atomic volumes of formation (,) and average ordering (excess) atomic volume (,) of formation of components Au and Cu; and volume mismatch degree.

Average atomic volume mismatch degree of characteristic atoms inside α component (α=Au or Cu) is

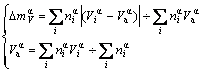             (5)

Average atomic volume mismatch degree of characteristic atoms between components Au and Cu is

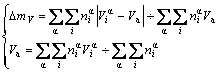          (6)

If there is no splitting atomic volume state, Eq.(6) becomes

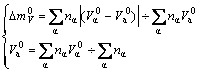             (7)

The total average atomic volume mismatch degree of a compound is

                (8)

In Eqs.(5)-(7),  and  are, respectively, atomic volume and number of the  characteristic atoms in a cell; , average atomic volume of the α-component; V_a, average atomic volume of the compound; atomic volume of the α-element; n_α, number of atoms of the α-component; n_T, total number of atoms in a cell; , average atomic volume of the element; V_a, average atomic volume of the compound.

 

2 Results

2.1 Volume sequences of  and  characteristic atoms

            The volume sequences of  and  characteristic atoms are separated out from the experimental average atomic volumes (V_AuCu=14.447 1×10^-3(nm³), V_AuCu= [17]) of L1₀-AuCu and L1₂-AuCu₃ compounds at room temperature by nine volume V-functions. The results are listed in Table 1, from which the following knowledge can be obtained.

            1) The volume sequences of the characteristic atoms obtained by nine V-functions are different each other.

            2) In the remainder of this section it has been demonstrated that the volumetric properties of alloy phases in the Au-Cu system should be described by the 6th V(x)-function. This means that the relation of and  with i is described by the following equation:

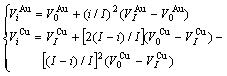         (9)

2.2 Volumetric properties of disordered Au_(1-x)Cu_x alloys

According to the volume sequences of characteristic atoms in Table 1, the volumes ,  and  of disordered Au_1-xCu_x alloys and their components as well as their volumes of formation  are calculated by the 2nd-9th V-functions, as listed in Table 2 and shown in Fig.2, from which the following knowledge can be obtained.

Table 2 Average volumetric properties V(x), V_Au(x), V_Cu(x) and ?V^m(x) of disordered Au_1-xCu_x alloys calculated by the 2nd-9th V-functions at room temperature (in 10^-3nm³)

Fig.2 Volumetric properties: (a), (b) Average atomic volumes (lattice parameters) V(x), V_Au(x) and V_Cu(x) (a(x), a_Au(x) and a_Cu(x)) of disordered Au_1-xCu_x alloys and their components calculated by the 6th V(x)-functions at room temperature, together with experimental lattice parameters[18-19]; (c) volumes of formation ?V^m(x) of disordered Au_1-xCu_x alloys calculated by the 2nd-9th V(x)-functions; (d) Deviations of average volumes of disordered Au_1-xCu_x alloys calculated by the 2nd-9th V-functions from ones calculated by the 6th V(x)-function; (e), (f) Concentrations  and of characteristic atoms in disordered Au_1-xCu_x alloys

1) The average atomic volumes  and lattice parameters  calculated by the 6th V(x)-function are in the best agreement with experimental values, and have positive deviation respectively from Zen’s law and Vegard’s law (details in Section 3.2).

2) The volumes of formation of disordered Au_1-xCu_x alloys calculated by the 2nd-9th V(x)-functions have positive values, in which the values obtained by the 6th V(x)-function is the largest.

 

2.3 Volumetric properties of ordered Au_1-xCu_x alloys

According to the volume sequences of characteristic atoms in Table 1, the volumes V(x),  and  of L1₂-Au₃Cu, L1₀-AuCu and L1₂-AuCu₃ type ordered Au_1-xCu_x alloys and their components as well as their volumes of formation ?V^m(x) and ordering volumes ?V^ex(x) are calculated by the 2nd-9th V(x)-functions. The volumetric properties of L1₂-Au₃Cu-type, L1₀-AuCu-type and L1₂-AuCu₃-type ordered Au_1-xCu_x alloys at room temperature are shown in Figs.3-5 and listed in Tables 3-6.

Table 3 Average volumetric properties V(x), V_Au(x), V_Cu(x), ?V^m(x) and ?V^ex(x) of L1₂-Au₃Cu-type ordered Au_1-xCu_x alloys with maximal ordering degree calculated by 2nd-9th V-functions at room temperature (in 10^-3nm³)

Table 4 Average volumetric properties V(x), V_Au(x), V_Cu(x), ?V^m(x) and ?V^ex(x) of L1₀-AuCu-type ordered Au_1-xCu_x alloys with maximal ordering degree calculated by the 2nd-9th V-functions at room temperature (in 10^-3nm³)

Table 5 Average volumetric properties V(x), V_Au(x), V_Cu(x), ?V^m(x) and ?V^ex(x) of L1₂-AuCu₃-type ordered Au_1-xCu_x alloys with maximal ordering degree calculated by 2nd-9th V-functions at room temperature (in 10^-3nm³)

Table 6 Lattice parameters a(x), a_Au(x), a_Cu(x), ?a^m(x), ?a^ex(x) of disordered with full disorder and ordered Au_1-xCu_x alloys with maximal ordering degree calculated by the 6th V-function (in 10^-1nm)

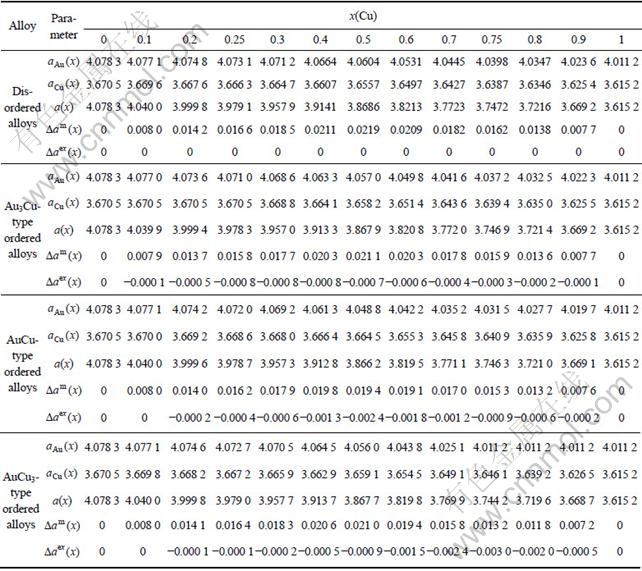
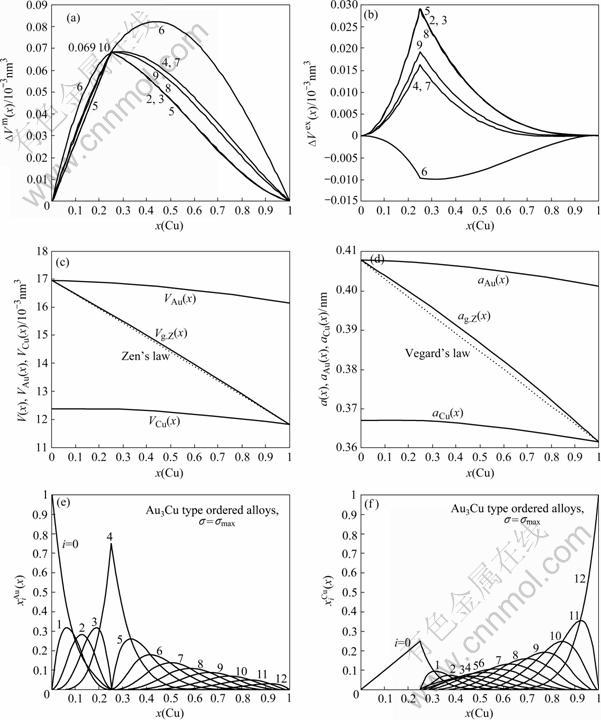
Fig.3 Formation of volume ?V^m(x) (a) and ordering volume ?V^ex(x) (b) of L1₂-Au₃Cu-type ordered Au_1-xCu_x alloys with maximal ordering degree calculated by the 2nd-9th V-functions at room temperature (in 10^-3nm³); average atomic volumes V(x), V_Au(x) and V_Cu(x) (c) and average lattice parameters a(x), a_Au(x) and a_Cu(x) (d) of L1₂-Au₃Cu-type ordered Au_1-xCu_x alloys with maximal ordering degree calculated by the 6th V-functions at room temperature; concentrations (e) and (f) of andcharacteristic atoms in L1₂-Au₃Cu-type ordered Au_1-xCu_x alloys

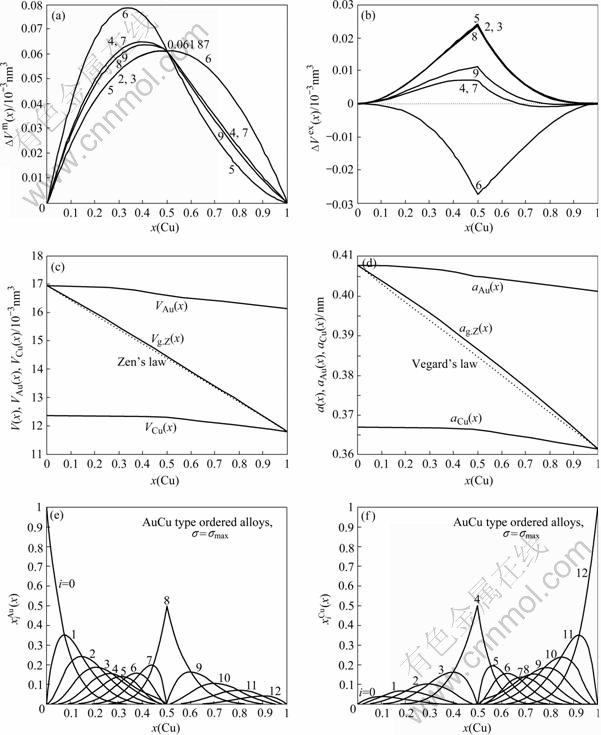
Fig.4  Formation of volume ?V^m(x) (a) and ordering volume ?V^ex(x) (b) of L1₀-AuCu-type ordered Au_1-xCu_x alloys with maximal ordering degree calculated by the 2nd-9th V-functions at room temperature; average atomic volumes V(x), V_Au(x) and V_Cu(x) (c) and average lattice parameters a(x), a_Au(x) and a_Cu(x) (d) of L1₀-AuCu-type ordered Au_1-xCu_x alloys with maximal ordering degree calculated by the 6th V-functions at room temperature; concentrations  (e) and  (f) of  and  characteristic atoms in L1₀-AuCu-type ordered Au_1-xCu_x alloys

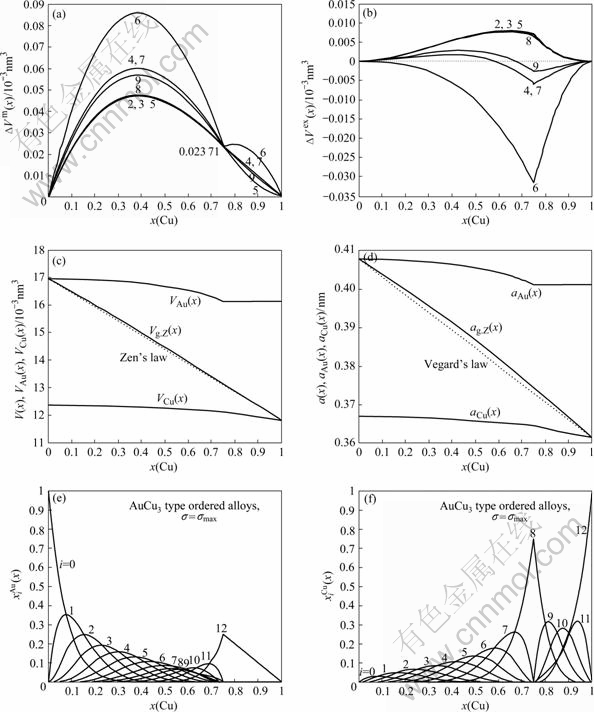
Fig.5 Formation of volume ?V^m(x) (a) and ordering volume ?V^ex(x) (b) of L1₂-AuCu₃-type ordered Au_1-xCu_x alloys with maximal ordering degree calculated by the 2nd-9th V-functions at room temperature; average atomic volumes V(x), V_Au(x) and V_Cu(x) (c) and average lattice parameters a(x), a_Au(x) and a_Cu(x) (d) of L1₂-AuCu₃-type ordered Au_1-xCu_x alloys with maximal ordering degree calculated by 6th V-functions at room temperature; concentrations  (e) and  (f) of  and  characteristic atoms in L1₂-AuCu₃-type -type ordered Au_1-xCu_x alloys

From these results the following knowledge can be obtained.

1) Even through the volume sequences of characteristic atoms in Table 1 are separated out from the experimental volumes of L1₀-AuCu and L1₂-AuCu₃ compounds only, the volumes of the L1₂-Au₃Cu compound calculated by the 2nd-9th V(x)-functions are equal each to each (15.740 8×10^-3nm^-3), and in good agreement with the experimental volume (15.773 1×10^-3nm^-3)[16], but their average atomic volumes  and  of Au and Cu components are different each other.

2) The volumes of the L1₀-AuCu compound calculated by the 2nd-9th V(x)-functions are equal to experimental volume (14.447 1×10^-3nm^-3), but their average atomic volumes  and  of Au and Cu components are different each other.

3) The volumes of the L1₂-AuCu₃ compound calculated by the 2nd-9th V(x)-functions are equal to experimental volume (13.122 5×10^-3nm^-3), but their average atomic volumes  and  of Au and Cu components are different each other.

4) Tables 3-5 show that the volumes of formation ?V^m(x) calculated by the 2nd-9th V(x)-functions are of positive values. But only the ordering volume ?V^ex(x) calculated by the 6th V(x)-function are negative, which is coincident with the experimental result. Therefore, only the 6th V(x)-function can be used to describe volumetric properties of Au-Cu system.

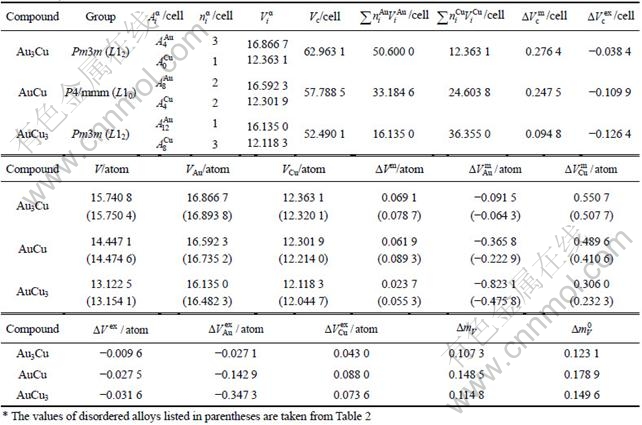
2.4 Volumetric properties of L1₂-Au₃Cu, L1₀-AuCu and L1₂-AuCu₃ compounds

From Table 7 following knowledge can be obtained: The volumetric properties of these three compounds are of the same results as listed in Tables 3-6. The volumes of formation of these three compounds are of positive values, to which the contribution of the Au-component is negative, the contribution of the Cu-component is positive, and  . The ordering volumes of these three compounds are of negative values, i.e., , to which the contribution of the Au-component is positive (, negative), the contribution of the Cu-component is negative (, positive), and   as disordering compounds. The volume mismatch degrees of characteristic atoms between constituents Au and Cu for these three compounds are smaller than those of atoms between pure elements Au and Cu, respectively. There is no volume mismatch degree  inside the component in these three compounds. But the AuCuⅡ with a long-period superlattice structure has one, which will be presented in the future.

Table 7 Volumetric properties of L1₀-AuCu, L1₂-AuCu₃ and L1₂-Au₃Cu compounds calculated by the 6th V-functions (V in 10^-3nm³, a in 10^-1nm)

3 Discussion and conclusions

3.1 Relation of volumes and potential energies of characteristic atoms

In the Au-Cu system, the volume change and potential energy change of  and  characteristic atoms consequence on changing nearest neighbor configuration indicated by i number of Cu-atoms have different correlations.

The relation of  and  with i is described by the following equation[13]:

           (10)

where =-368 kJ/mol, =-391.303 kJ/mol, =-336 kJ/mol, =-352.055 kJ/mol.

By comparing Eqs.(9) and (10), the following knowledges can be obtained: for the Au-characteristic atoms, the potential energy lowers with increasing the i number of Cu-atoms, and the volume reduces. For the Cu-characteristic atoms, the potential energy lowers with increasing the (I-i) number of Au-atoms, but the volume rises.

This different correlation will be explained by electronic structure sequences of  and  characteristic atoms in the future.

 

3.2 Relation between Zen’s law and general Zen’s law

In Pearson’s book of 1972, “The crystal chemistry and physical of metals and alloys”[20], we are informed that there is a Zen’s law. The average atomic volume of a solid solution is the concentration-weighted average of the atomic volumes of the elements. For Au-Cu alloys, it is

                  (11)

According the SSA framework, the average atomic volume of an alloy is the concentration (,)- weighted average of the splitting atomic volumes () of the characteristic atoms, represented by Eq.(6), which may be named as additive law of characteristic atomic volume. It has been demonstrated that the equation of average atomic volume of intermetallic compounds, ordered and disordered alloys for Au-Cu system is

               (12)

For the disordered alloys only, Eq.(12) becomes

                 (13)

where =16.958 11×10^-3nm³, =16.135 05×10^-3nm³, =11.812 37×10^-3nm³, =12.363 12×10^-3nm³.

If after forming solid solution there is no splitting of atomic volume state, Eqs.(12) and (13) become into Eq.(11). Therefore, the additive law of volumes of characteristic atoms may be also named as the general Zen’s law.

 

3.3 Relation between Vegard’s law and general Vegard’s law

The Vegard’s law indicates that the average lattice parameter of a solid solution is the concentration- weighted average of the lattice parameters (,) of the constituent elements. For Au_1-xCu_x alloys, it is:

                     (14)

In the SSA framework, the average lattice parameter of an alloy may be similarly obtained by the concentration (,)-weighted average of the lattice parameter (,) of the characteristic crystals, which may be thought to be obtained by splitting lattice parameter states of the constituent elements. If we use the lattice parameters of characteristic crystal instead of volumes of corresponding characteristic atoms, Eqs.(12) and (13) become, respectively

                  (15)

(16)

where, =0.407 83 nm, =0.401 12 nm, = 0.361 52 nm, =0.367 05 nm.

If there is no split of lattice parameter state, Eqs.(15) and (16) become Eq.(14). Therefore, the additive law of lattice parameter of characteristic crystals may be also named as the general Vegard’s law.

3.4 Difference between Vegard’s law and Zen’s law

The lattice parameter  of disordered Au_1-xCu_x alloys can be obtained approximately by Vegard’s law and by Zen’s law. The latter may be rewritten as

           (17)

Eqs.(14) and (17) are not equal in value. In order to understand the difference between Vegard’s law and Zen’s law, the first and the second derivative of  and  with respect to x have been obtained, respectively:

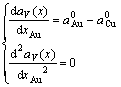                        (18)

    (19)

From Eqs.(18) and (19), it can be known that the  is a linear function of concentration x, and the  is a convex function of concentration x. This means that  in the range . Using the same method, it can be demonstrated that .

We suggest that the general Zen’s law should be adopted in theory, because the volume is an extensive property, which obeys the additive law (Eq.(1)), but the lattice parameter is not extensive property.

 

3.5 Relationship between partial and average molar (atomic) properties of components

In the SSA framework, the integral extensive property q of a given alloy is described directly by combination of the average molar (atomic) properties q_A and q_B of A- and B-components (see Eq.(1)).

The traditional thermodynamics of alloys is a framework of the total energy and total volume unable to be separated. Therefore, the integral extensive property of a given alloy is described indirectly by the partial molar properties  and of A- and B-components [21]:

                    (20)

According to definition of the partial molar property[21], it can be derived that

                 (21)

The general relation expression between the partial and average molar properties of alloy components have been established:

       (22)

The partial molar (atomic) property functions derived from nine q(x)-functions of binary disordered alloys are shown in Table 8.

Table 8 Nine partial molar (atomic) property -functions of binary disordered alloys in SSA framework

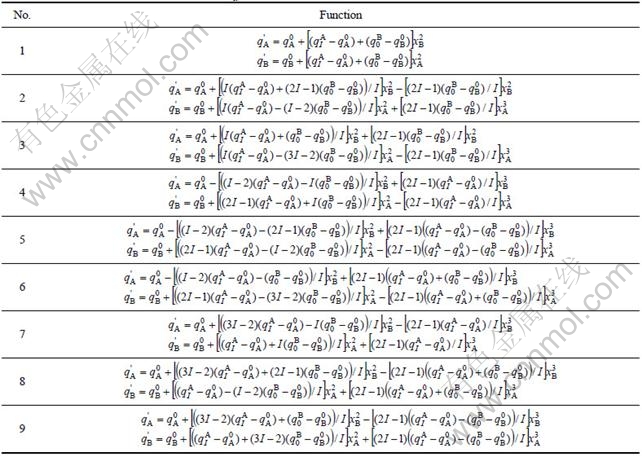
From these equations, the following inferences can be drawn.

1) From Eq.(21), it can be known that the partial molar properties  and  are dependent on the integral property function, but independent on it is combinational means of average molar properties of alloy components. This means that their partial properties do not represent the average properties of components.

2) From Eq.(22), the identical equation between the integral property of the partial molar properties and the combinational property of the average molar properties of components can be derived:

       (23)

3) From Eq.(22), the differential equation and its constraining equation between partial and average molar properties can be derived, respectively,

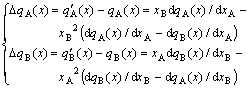     (24)

and

                    (25)

4) From Eq.(22), the Gibbs-Duhem equation can be derived:

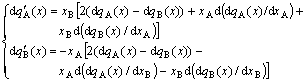
                    (26)

 

3.6 Relationship between lattice parameter and ordering degree of Au₃Cu-, AuCu- and AuCu₃-type ordered alloys

The relationship between the lattice parameter and ordering degree σ of compounds like AuCu₃ cannot be reliably measured, since the accessible equilibrium range of long range ordering σ is too limited. This difficulty was side-stepped by GIALANELLA et al[22-23], who used a ball-mill to progressively destroy ordering degree in Ni₃Al, which has the same superlattice as AuCu₃. In the SSA framework, this relation can be satisfactorily described. The results are shown in Figs.6 and 7.

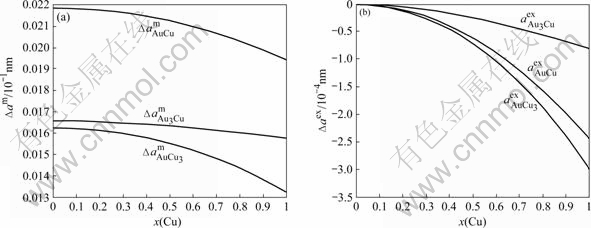
Fig.6 Relationship between lattice parameter and ordering degree for L1₂-Au₃Cu, L1₀-AuCu and L1₂-AuCu₃ compounds

Fig.7 Relationship between lattice parameter and ordering degree for L1₂-Au₃Cu, L1₀-AuCu and L1₂-AuCu₃ type ordered alloys

References

[1] XIE You-qing, TAO Hui-jing, PENG Hong-jian, LI Xiao-bo, LIU Xin-bi, PENG Kun. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC TiAl₂ type alloys [J]. Physica B, 2005, 366: 17-37.

[2] XIE You-qing, PENG Kun, LIU Xin-bi. Influences of x_Ti/x_Al on atomic states, lattice constants and potential energy planes of ordered FCC TiAl-type alloys [J]. Physica B, 2004, 344: 5-20.

[3] XIE You-qing, LIU Xin-bi, PENG Kun, PENG Hong-jian. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC TiAl₃-type alloys [J]. Physica B, 2004, 353: 15-33.

[4] XIE You-qing, PENG Hong-jian, LIU Xin-bi, PENG Kun. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC Ti₃Al-type alloys [J]. Physica B, 2005, 362: 1-17.

[5] LUPIS C P P. Chemical thermodynamics of materials [M]. Amsterdam: North-Holland, 1983. 438-469.

[6] KIKUCHI R. A theory of cooperative phenomena [J]. Phys Rev, 1951, 81: 988-1003.

[7] ASTA M, de FONTAIN D, van SCHILFGAARDE M, SLUITER M, ATHFESSEL M. First-principles phase-stability of fcc alloys in the Ti-Al system [J]. Phys Rev, 1992, 46: 5055-5072.

[8] ASTA M, de FONTAIN D, van SCHILFGAARDE M. First-principles study of phase stability of Ti-Al intermetallic compounds [J]. Mater Res, 1993, 8: 2554-2568.

[9] SUNDMAN B, FRIES S G, OATES A W. A calphad assessment of the Au-Cu system using the cluster variation method [J]. Z Metallkd, 1999, 90: 267-273.

[10] XIE You-qing. Atomic energies and Gibbs energy functions of Ag-Cu alloys [J]. Science in China (series E), 1998, 41: 146-156.

[11] XIE You-qing, ZHANG Xiao-dong. Atomic volumes and volumes functions of Ag-Cu alloys [J]. Science in China (series E), 1998, 41: 157-168.

[12] XIE You-qing, LI Xiao-bo, LIU Xin-bi, PENG Hong-jian, NIE Yao-zhuang. Potential energy sequences of characteristic atoms on basis of heats of formation of disordered Au_(1-x)Cu_x alloys(I) [J]. Journal of Materials Science and Engineering, 2009, 3: 51-68.

[13] XIE You-qing, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, NIE Yao-zhuang. Potential energies of characteristic atoms on basis of experimental heats of formation of AuCu and AuCu₃ compounds (I) [J]. Trans Nonferrous Met Soc China, 2009, 19(5): 1243-1256.

[14] XIE You-qing, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, NIE Yao-zhuang. Potential energy sequences of characteristic atoms on basis of heats of formation of disordered Au_(1-x)Cu_x alloys(II). [J]. Journal of Materials Science and Engineering, 2009, 6: 44-57.

[15] XIE You-qing, LIU Xin-bi, LI Xiao-bo, PENG Hong-jian, NIE Yao-zhuang. Potential energies of characteristic atoms on basis of experimental heats of formation of AuCu and AuCu₃ compounds (II) [J]. Trans Nonferrous Met Soc China, 2009, 19(5): 1257-1270.

[16] CAHN R W. Lattice parameter changes on the disordering intermetallies, Intermeter and volume changes on disordering intermetallies [J]. Intermetallics, 1999, 7: 1089-1094.

[17] BHATIA M L, CAHN R W. Lattice parameter and volume changes on disordering intermetallics [J]. Intermetallics, 2005, 13: 474-483.

[18] LU S S, LIANG C K. Existence of the CuAu₃ long-range order in the Cu-Au system [J]. K’o Hsueh T’ung Pao, 1966, 17(9): 395-396. in Chinese (Crys structure; experimental) .

[19] VEGARD L, DALE H. An investigation of mixed crystals and alloys [J]. Z Kristallogr, 1928, 67: 148-161. (in German) (Equi. Diagram, Crys structure; experimental).

[20] PEARSON W B. The chemistry and physics of metals and alloys [M]. New Youk: Wiley-Interscience, 1972.

[21] WALTER J M. Physical chemistry [M]. London: Longman Group limited, 1976: 230.

[22] GIALANELLA S, NEWCOMB S, CAHN R W. Ordering and disordering of alloys [M]. London: Elsevier Applied Science, 1992: 67.

[23] GIALANELLA S, CAHN R W, MALAGELADA J, SURI?ACH S, BAR?M D, YAVARI A R. Kinetics of ordering transformations in metals [M]. Warrendale, P.A: TMS, 1992: 161.

                     

Foundation item: Project(50471058) supported by the National Natural Science Foundation of China; Project(08JJ3099) supported by the Natural Science Foundation of Hunan Province, China

Corresponding author: XIE You-qing; Tel: +86-731-88879287; E-mail: xieyouq2000@yahoo.com.cn

DOI: 10.1016/S1003-6326(09)60077-7

(Edited by YANG Hua)