DOI： 10.11817/j.issn.1672-7207.2019.09.019

膨润土膨胀力长期衰减特性的数值分析

李晓月,姜昊,徐永福

（上海交通大学 船舶海洋与建筑工程学院，上海，200240）

摘要:利用Phreeqc软件对膨润土缓冲层在多场耦合作用下10 000 a内的孔隙溶液浓度、晶层离子交换量及蒙脱石含量变化进行数值模拟，并结合分形理论，计算得到膨润土垫层的膨胀力在长时间尺度下的衰减变化过程。研究结果表明：膨胀力衰减幅度由膨润土垫层与围岩接触的外边界至内部逐步降低；海水环境中膨胀力衰减较地下淡水环境更为显著；膨润土的膨胀力经一段时间衰减后趋于稳定且10 000 a后仍存在较高膨胀力，证明膨润土能长久地有效确保核废料处置库的安全性。

关键词:膨润土；核废料；膨胀力衰减；分形理论

中图分类号:TU443    文献标志码:文献标识码:A     文章编号:1672-7207（2019）09-2226-07

Numerical simulation of bentonite swelling attenuation processes in long time scale

LI　Xiaoyue, JIANG　Hao, XU　Yongfu

(School of Naval Architecture, Ocean & Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

Abstract: By using software Phreeqc, the pore solution concentration change, crystal layer ions exchange capacity and the variation in content of the montmorillonite were simulated under the effect of multi-field coupling during 10 000 a. Bentonite swelling force attenuation processes in long time scale were obtained based on fractal theory. The results show that the swelling force becomes stable with time increasing and the attenuation decreases along the bentonite buffer from the boundary contacted with external rock mass to interior. The attenuation of the swelling force in seawater is more significant than that in the groundwater, and the expansion force of bentonite tends to be stable after a period of attenuation and still obtains a relative high value after 10 000 a. Thus, bentonite is certainly a secure material in nuclear waste disposal repository environment.

Key words: bentonite; nuclear waste; swelling attenuation processes; fractal theory

压实膨润土遇水可发生膨胀，填充围岩裂隙，形成防渗层，从而避免核废料向周围环境释放，因此被用于核废料处置库的缓冲层。但地下核废料处置库的环境复杂，膨润土的膨胀性会在多种因素的耦合作用下发生变化^[1-2]。研究膨润土的膨胀性在多种不同因素影响下的变化对评估核废料处置库的安全性具有重要意义。秦冰等^[3-4]发现了GMZ01膨润土试样的膨胀率会受到干密度、浸泡液成分、浓度及竖向压力的影响，并利用改进的三向胀缩仪进行了三向膨胀力试验；孙德安等^[5]对膨润土进行了不同浓度溶液下的膨胀试验，发现膨润土的孔隙比与膨胀力在双对数坐标中呈线性关系；叶为民等^[6-7]通过利用泵压法研究GMZ01微观孔隙，得到了膨润土自由膨胀的水土特征和体变特征，并发现在不同浓度NaCl溶液中饱和的膨润土孔隙比在相同荷载下随溶液浓度增加而减小。除溶液浓度对膨胀作用的抑制外，蒙脱石与溶液发生化学反应也会造成膨胀力的衰减。SCHRAMM^[8]发现蒙脱石表面吸附的Na⁺与溶液中阳离子发生置换反应会使膨胀力减小；SAVAGE等^[9]发现蒙脱石与溶液中物质发生化学反应会溶解并产生相应的非膨胀性次生矿物；陈宝等^[10]通过实验发现蒙脱石的溶解现象，蒙脱石含量减小将导致膨胀力衰减。针对核废料处置库自身的特殊性，工程上通常要求确保其在数万年内的安全性，但传统的岩土领域测试方法无法实现对膨润土在长时间尺度下膨胀力衰减过程的准确预测。数值模拟方法可用来研究处置库中膨润土的膨胀性能变化，并已在相关实验研究与工程实践中取得了一定成果。MONTES等^[11]利用KIRMAT程序模拟计算出长时间尺度下膨润土化学反应引起矿物体积变化过程，并以此为基础研究了膨润土的膨胀衰减；ALONSO等^[12]提出巴塞罗那膨胀模型，并开发了CODE_BRIGHT程序，可模拟出膨润土在温度、渗流、围岩应力耦合作用下膨胀性的变化；ZHENG等^[13]基于FEBEX模型实验，模拟了Opalinus黏土在地下处置库环境中的膨胀衰减情况。为了分析膨润土垫层在10 000 a内的膨胀衰减情况，本文作者利用Phreeqc软件建立了一维离子运移反应模型，研究10 000 a内钠基膨润土分别在地下淡水和海水中的孔隙溶液浓度及组分、蒙脱石孔隙率的分布及变化，并结合分形理论，提出高压实钠基膨润土在地下淡水和海水环境中，其膨胀力在时间尺度下衰减情况的预测方法。

1 计算模型

1.1　理论基础

为对处置库垫层中的膨润土膨胀性进行预测，可利用蒙脱石孔隙比V_w/V_m和有效应力p_e的关系^[14]：

(1)

式中：V_w为蒙脱石颗粒吸收水的体积；V_m为膨润土中蒙脱石的体积；K为膨胀系数，与膨润土表面离子种类及分布相关，可通过双电层理论与分形理论相结合计算得到^[15]；D_s为颗粒表面维度，可利用氮吸附试验测得^[16]，本研究所用的高庙子钠基膨润土D_s=2.65。

在蒸馏水中，有效应力p_e等于竖向外荷载p；在盐溶液中，受溶液渗透吸力的影响，作用在膨润土上的有效应力p_e分为外部施加的竖向荷载p及随孔隙水浓度增加而增大的渗透压力p_π^[17]：

(2)

膨润土的总膨胀力p_e在盐溶液中被渗透应力抵消一部分p_π，所剩的表观膨胀力等于p，因此，p是衡量膨润土膨胀性在工程应用中可靠与否的关键。根据分形理论，可得到作用于膨润土晶粒上的渗透应力p_π与溶液产生的渗透吸力π的关系^[14]：

(3)

根据van's Hoff公式，溶液渗透吸力π为

(4)

式中：为溶质解离数；R为气体常数(8.31 J/(mol·K))；T为热力学温度；m为溶质浓度(mol/L)。

由式(2)和(3)可得盐溶液中膨润土所受的有效应力为

(5)

式(5)经不同浓度下的多组试验数据得到验证^[14]，因此，可以较准确地预测在长时间尺度下核废料处置库中的膨润土膨胀力变化情况。

在膨润土的衰减过程中，地下流体中的溶质通过扩散进入孔隙中造成孔隙水浓度变化，并会与蒙脱石发生化学反应引起膨胀系数K和蒙脱石孔隙比变化。为保证核废料处置库长时间的稳定性，需利用数值模拟得到长时间尺度下孔隙溶液浓度及蒙脱石含量变化，计算出不同浓度下溶液的渗透吸力π、蒙脱石孔隙比V_w/V_m及膨胀系数K，通过式(1)得到有效应力p_e，进而利用式(5)求出外部荷载p，即有效保证处置库安全的净膨胀力。

1.2　数值模型描述

基于膨润土吸水饱和后与地下流体中的化学元素发生反应，建立一维运移反应模型。假设外部边界温度为100 ℃，膨润土厚度为1 m，分20个宽度均为5 cm的单元进行计算。左边界与基岩接触，为渗透自由边界；右边界与处置罐接触，为渗透封闭边界。膨润土矿物成分^[18]及基本物理参数分别见表1和表2，地下流体溶液组分^[19]见表3，数值模型如图1所示。

核废料处置库的选址多在人烟稀少且罕有地质灾害的内陆，因此，地下水成分一般比较稳定且为淡水。本文仅根据以往文献设定初始地下溶液成分并进行定性分析，针对具体实际工程则应当依据实际测得的地下流体成分进行计算。在长时间尺度内，考虑到地下流体成分可能发生变化，应对地下溶液成分间断地多次测量，从而不断修正结果，保证计算的准确性。

表1　高庙子膨润土矿物成分及热力学常数K_m^[18]

Table 1　Mineral composition and thermodynamic equilibrium constants of Gaomiaozi bentonite^[18]

表2　膨润土参数

Table 2　Parameters of bentonite

表3　地质流体离子浓度^[19]

Table 3　Ion content of geological fluid^[19]

图1　数值模拟模型示意图

Fig. 1　Schematic representation of simulations

膨润土在处置库中先发生相对时间尺度较短（3~4 a）的吸水膨胀过程至饱和后，进入可能长达上千年的膨胀衰减阶段^[20]。为便于研究膨润土的膨胀衰减过程，将膨胀饱和过程结束状态作为衰减过程初始状态进行分析。由于深地处置库中的膨润土经高压实处理且膨胀受限，膨润土晶层间距很小，因此，可认为膨润土仅发生晶层膨胀。此时，水分子以偶极子的形式通过静电力在晶层表面形成定向排列的水分子^[21]，这些水分子吸附在晶体表面不参与渗流及化学反应，仅考虑溶质在饱和高压实膨润土中以缓慢的离子扩散形式运移，依据LEHIKOINE等^[22]的相关研究，扩散系数取10^-11 m²/s。在构建模型时，主要关注膨胀衰减的过程，将膨润土的饱和状态作为初始状态，认为膨润土与地质流体间化学反应在饱和状态下进行；由于在高压实膨润土中流体渗透系数极低^[23]，模型不考虑地下流体的对流，认为孔隙流体是静止的，仅考虑离子的扩散作用；仅考虑Na⁺，K⁺，Ca²⁺和Mg²⁺这4种主要阳离子迁移扩散及其之间交换性对溶液浓度变化的影响，忽略其他阳离子的影响^[24]；核废料衰变放热过程中，考虑到膨润土的良好导热性，相对膨润土膨胀及衰减的时间尺度，导热过程所用时间可忽略，因此，认为整个系统中温度是稳定的；由于核废料处置库为封闭环境含氧量有限，且金属罐发生氧化反应会迅速耗尽氧气，因此，认为反应环境为还原反应。

2 结果与分析

2.1　孔隙水中溶质浓度变化

地下流体中的溶质从自由边界向膨润土内部逐步扩散，导致膨润土中孔隙水浓度由外至内发生变化，如图2所示。从图2可见：同一深度的膨润土孔隙溶液浓度随时间增加而增加，临近外边界处孔隙水浓度增加速率比内部的大，率先达到外部环境的溶液浓度。在5 000 a左右，整个膨润土垫层的孔隙浓度均近似达到外部溶液浓度水平并达到稳定。相对于地下淡水环境，海水中溶液浓度更高，对膨润土垫层孔隙溶液浓度的影响更显著。地下淡水环境中，5 000 a后达到稳定的浓度约为0.16 mol/L，而在海水中，500 a时浓度已经达到0.2 mol/L以上，稳定后孔隙浓度约1.15 mol/L。可见，外部环境中的溶液浓度越高，压实垫层的孔隙溶液浓度增长速度越快，且最终达到与外部溶液相同的浓度。从图2还可见，经过长时间后溶质浓度从外到内会略有升高趋势，对此可考虑为内部离子发生富集。

膨润土孔隙溶液浓度受扩散时间长短、不同深度位置及外界溶液离子浓度影响而显现出差异。利用在给定外界溶液环境中某一时刻的孔隙溶液浓度空间分布情况，可计算出各时段不同空间位置由溶液浓度引起的溶液渗透吸力π。

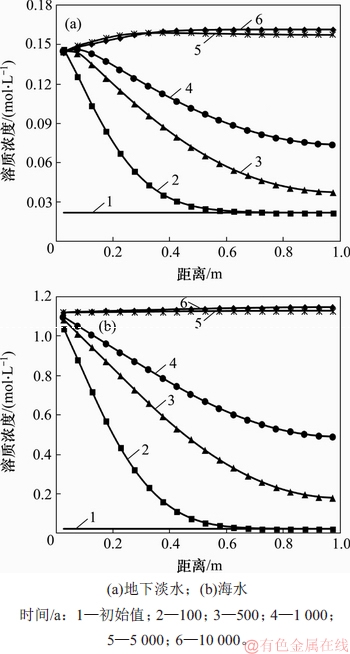
图2　不同位置下溶液浓度变化

Fig. 2　Solution concentration changes in different distances

2.2　蒙脱石膨胀系数K的变化

当蒙脱石晶层间距足够大以形成扩散离子双电层时，双电层理论可以较为准确地计算出膨胀力，而分形理论也适用于渗透膨胀的情况，因此，可以认为2种理论的计算值相等。根据孔隙溶液种类、浓度及蒙脱石表面阳离子种类及含量，可利用双电层理论计算出有效应力p_e及蒙脱石孔隙比V_w/V_m，再结合式(1)计算得到膨胀系数K^[15]。地下流体渗入膨润土垫层中，膨润土表面的Na⁺与地下流体中的Ca²⁺和K⁺发生置换反应，会造成膨胀系数K的变化。根据蒙脱石膨胀系数K的计算方法^[15]，先利用数值模拟，得到各点在各时间段内不同离子组分浓度空间分布情况，再将双电层与分形理论相结合求出K，结果见图3。

膨润土与溶液中溶质发生的置换反应随溶质扩散进程由左侧自由边界向内部逐步发生。外边界发生的离子交换过程先于内部且更为充分，而膨润土表面阳离子由Na⁺置换为Ca²⁺或K⁺后膨胀系数K会减小，因此越靠近膨润土左侧自由边界处，K衰减幅度越大。在模拟得到的10 000 a内地下淡水环境中K的变化情况可看出，同一位置处K随时间增加逐步减小且衰减影响范围逐步深入至0.6 m。但在10 000 a时，大于0.6 m深度处，K仍未受到影响。

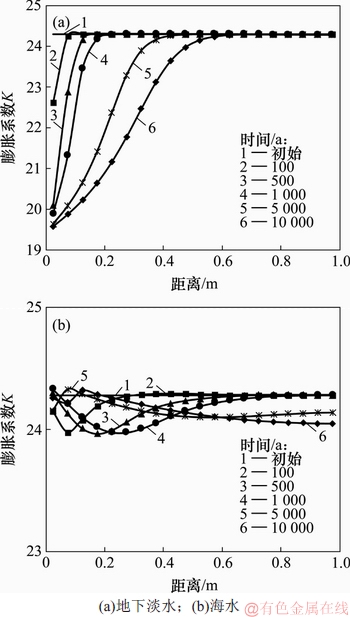
图3　不同位置下膨胀系数K变化

Fig. 3　Swelling parameter K changes in different distances

相对于地下淡水环境，海水中离子含量更高，边界溶液浓度高，扩散更加深入，膨胀系数K受影响范围更大。从图3(b)可以看出，在整个膨润土的空间尺度范围内K均受外部溶液影响，且由于不同离子的扩散速率差异而发生波动。但10 000 a内的变化中，在海水环境下缓冲层整个范围内的K基本都在24以上，而在淡水环境中，从近一半深度处至自由边界处，K逐渐从24减小到19.5。从化学平衡角度分析，海水中存在的大量钠离子会抑制膨润土中的钠离子与其他离子发生置换。因此，在海水中，尽管受影响范围广且略有减小，但由于受Na⁺的影响，K仍比地下淡水中的大。

2.3　孔隙比V_w/V_m变化

蒙脱石与地下水溶液中物质发生化学反应，会导致蒙脱石变性。部分可膨胀的蒙脱石溶解或者转化为不再具有膨胀性的矿物^[10]，造成蒙脱石孔隙比增大，引起膨胀性的衰减。图4所示为不同时间尺度下，孔隙比与距离的关系。从图4可知，无论是处于地下淡水环境还是海水环境，在临近外部溶液的自由边界附近，孔隙比随时间变化增加明显。由于海水环境中的溶液浓度相对更高，蒙脱石变性速率均略比淡水中的快。但随距离深入孔隙比变化逐步减小，直至深度大于约0.13 m，孔隙比不再变化。而在外边界处，孔隙比趋近无穷大，表明自由边界处具有膨胀性的蒙脱石几乎完全转化为不可膨胀的矿物。由式(1)可知，此时边界处膨胀力近似为0，膨润土失效。因此，尽管由蒙脱石与地下水发生化学反应造成的膨润土变性范围较小，但其对膨胀衰减影响不容忽略。

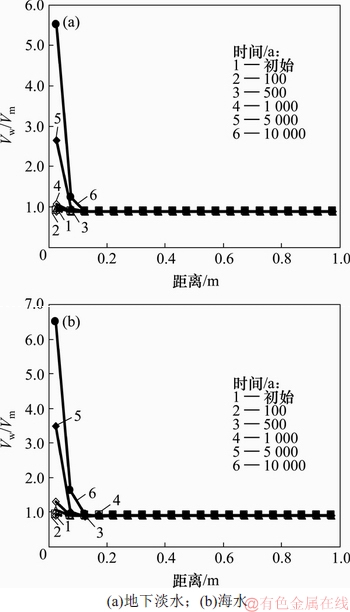
图4　孔隙比与距离的关系

Fig. 4　Relationship between void ratio and distance

2.4　膨胀力p的变化

由式(1)可知，膨胀力受孔隙水浓度、膨胀系数K及蒙脱石孔隙比3种因素共同影响。图5所示为在地下淡水和海水环境中，膨胀力在不同时间下的空间分布情况。可见：在整个空间的范围内，膨胀力随时间增加均有不同幅度衰减。相对于内部，垫层临近外边界处的孔隙浓度更高，产生的渗透应力p_π更大，离子交换量更大，K减小更明显，蒙脱石变性引起的孔隙比增加幅度更大。因此，外边界膨胀力衰减幅度远比内部的大，自由边界处膨胀力几乎衰减为0。在10 000 a时，地下淡水环境中内部膨胀力为9 MPa，海水环境中为6.2 MPa，可见核废料处置库中的膨润土经长时间发展变化，内部仍保有一定的膨胀力，其作为缓冲层在长时间尺度下具有较强的稳定性。

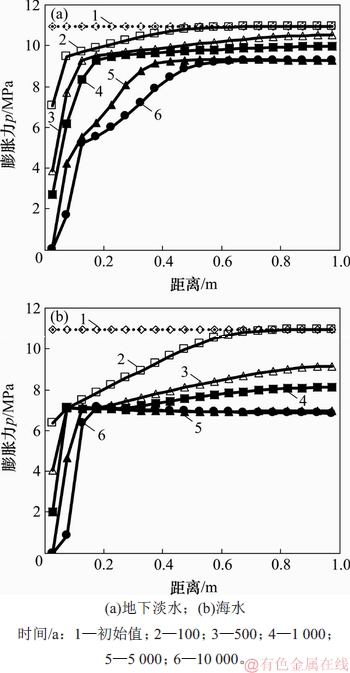
图5　膨胀力随时间的变化

Fig. 5　Swelling attenuation processes over time

通过淡水和海水2种环境的对比可知：外部溶液浓度越大对膨润土的膨胀衰减作用越强。但值得注意的是，在海水环境中，10 000 a时距外部约0.15 m深度处的膨胀力已经达到稳定值，而在地下淡水环境中，膨润土垫层从外边界直至0.5 m深度的范围内膨胀力仍有较大变化。在海水环境中，靠近外边界处的膨胀系数K比淡水环境中的大，导致膨胀力也比淡水环境中的大。而在膨润土垫层内部，2种溶液环境的膨胀系数K近似，此时溶液浓度对膨润土膨胀力的影响占主导因素，最终导致内部膨润土在浓度更高的海水环境下的膨胀力更小。因此，适当浓度的钠离子可以对维持膨润土较高的膨胀系数K、保障膨胀力的稳定性起到积极作用。

3 结论

1) 通过数值模拟得到了长时间尺度下饱和高庙子钠基膨润土在地下淡水及海水中膨润土孔隙水浓度及孔隙比的空间分布情况，并计算得到不同位置处的膨胀系数K。

2) 综合考虑蒙脱石孔隙浓度、膨胀系数K及孔隙比对膨胀力衰减的影响，结合分形理论计算得到钠基膨润土10 000 a内的膨胀力衰减变化过程，认为膨润土垫层能有效保障处置库的稳定性。

3) 外界浓度越高，膨胀力衰减幅度越大，但是适当浓度的钠离子能对提高膨润土的膨胀系数K，对提高膨胀力的稳定性起到积极的作用。

参考文献：

[1] XU Y F, MATSUOKA H, SUN D A. Swelling characteristics of fractal-textured bentonite and its mixtures[J]. Applied Clay Science, 2003, 22(4): 197-209.

[2] 姜昊, 徐永福, 项国圣. 膨润土的膨胀性衰减研究[J]. 地下空间与工程学报, 2016, 12(5): 1247-1253.

JIANG Hao, XU Yongfu, XIANG Guosheng. Research of the swelling capacity decay of bentonite[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(5): 1247-1253.

[3] 秦冰, 陈正汉, 刘月妙, 等. 高庙子膨润土的胀缩变形特性及其影响因素研究[J]. 岩土工程学报, 2008, 30(7): 1005-1010.

QIN Bing, CHEN Zhenghan, LIU Yuemiao, et al. Swelling-shrinkage behaviour of Gaomiaozi bentonite[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(7): 1005-1010.

[4] 秦冰, 陈正汉, 刘月妙, 等. 高庙子膨润土GMZ001三向膨胀力特性研究[J]. 岩土工程学报, 2009, 31(5): 756-763.

QIN Bing, CHEN Zhenghan, LIU Yuemiao, et al. Characteristics of 3D swelling pressure of GMZ001 bentonite[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(5): 756-763.

[5] 孙德安, 张龙. 盐溶液饱和高庙子膨润土膨胀特性及预测[J]. 岩土力学, 2013, 34(10): 2790-2795.

SUN Dean, ZHANG Long. Swelling characteristics of Gaomiaozi bentonite saturated by salt solution and their prediction[J]. Rock and Soil Mechanics, 2013, 34(10): 2790-2795.

[6] 叶为民, 钱丽鑫, 陈宝, 等. 高压实高庙子膨润土的微观结构特征[J]. 同济大学学报(自然科学版), 2009, 37(1): 31-35.

YE Weimin, QIAN Lixin, CHEN Bao, et al. Characteristics of micro-structure of densely compacted Gaomiaozi bentonite[J]. Journal of Tongji University(Natural Science), 2009, 37(1): 31-35.

[7] 叶为民, 黄伟, 陈宝, 等. 双电层理论与高庙子膨润土的体变特征[J]. 岩土力学, 2009, 30(7): 1899-1903.

YE Weimin, HUANG Wei, CHEN Bao, et al. Diffuse double layer theory and volume change behavior of densely compacted Gaomiaozi bentonite[J]. Rock and Soil Mechanics, 2009, 30(7): 1899-1903.

[8] SCHRAMM L L. Influence of exchangeable cation composition on the size and shape of montmorillonite particles in dilute suspension[J]. Clays and Clay Minerals, 1982, 30(1): 40-48.

[9] SAVAGE D, WALKER C, ARTHUR R, et al. Alteration of bentonite by hyper-alkaline fluids: a review of the role of secondary minerals[J]. Physics and Chemistry Earth, Parts A/B/C, 2007, 32(1/2/3/4/5/6/7): 287-297.

[10] 陈宝, 张会新, 陈萍. 高碱性溶液对高庙子膨润土溶蚀作用的研究[J]. 岩石力学与工程学报, 2012, 31(7): 1478-1483.

CHEN Bao, ZHANG Huixin, CHEN Ping. Geochemical interactions between compacted Gaomiaozi bentonite and hyper-alkaline solution[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(7): 1478-1483.

[11] MONTES H G, FRITZ B, CLEMENT A, et al. A simplified method to evaluate the swelling capacity evolution of a bentonite barrier related to geochemical transformations[J]. Applied Geochemistry, 2005, 20(2): 409-422.

[12] ALONSO E E, ALCOVERRO J, COSTE F, et al. The FEBEX benchmark test: case definition and comparison of modelling approaches[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(5/6): 611-638.

[13] ZHENG Liange, SAMPER J, MONTENEGRO L. A coupled THC model of the FEBEX in situ test with bentonite swelling and chemical and thermal osmosis[J]. Journal of Contaminant Hydrology, 2011, 126(1/2): 45-60.

[14] XU Yongfu, XIANG Guosheng, JIANG Hao, et al. Role of osmotic suction in volume change of clays in salt solution[J]. Applied Clay Science, 2014, 101: 354-361.

[15] 项国圣, 姜昊, 徐永福. 压实膨润土膨胀变形的分形计算方法[J]. 岩土力学, 2015, 36(4): 1009-1014.

XIANG Guosheng, JIANG Hao, XU Yongfu. Fractal calculation method for swelling deformation of compacted bentonite[J]. Rock and Soil Mechanics, 2015, 36(4): 1009-1014.

[16] 项国圣, 徐永福, 姜昊. 膨润土表面分维的试验确定[J]. 地下空间与工程学报, 2016, 12(2): 369-373.

XIANG Guosheng, XU Yongfu, JIANG Hao. Test determination for the surface fractal dimension of bentonite[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(2): 369-373.

[17] RAO S M, THYAGARAJ T. Swell-compression behaviour of compacted clays under chemical gradients[J]. Canadian Geotechnical Journal, 2007, 44(5): 520-532.

[18] 钱丽鑫. 高放废物深层地质处置库缓冲材料[D]. 上海: 同济大学土木工程学院, 2007: 83-90.

QIAN Lixin. A fundamental study of GMZ bentonite as buffer material in deep geological disposal for high-level radioactive waste[D]. Shanghai:Tongji University. College of Civil Engineering, 2007: 83-90.

[19] WERSIN P. Geochemical modelling of bentonite pore water in high-level waste repositories[J]. Journal of Contaminant Hydrology, 2003, 61(1/2/3/4): 405-422.

[20] YONG R N. Overview of modeling of clay microstructure and interactions for prediction of waste isolation barrier performance[J]. Engineering Geology, 1999, 54(1/2): 83-91.

[21] AVNIR D, JARONIEC M. An isotherm equation for adsorption on fractal surfaces of heterogeneous porous materials[J]. Langmuir, 1989, 5(6): 1431-1433.

[22] LEHIKOINEN J, CARLSSON T, MUURINEN A, et al. Evaluation of factors affecting diffusion in compacted bentonite[J]. Material Research Society Symposium Proceedings, 1995, 412: 675.

[23] 牛文杰, 叶为民, 陈宝, 等. 高庙子膨润土的土水特征曲线与渗透系数[J]. 地下空间与工程学报, 2009, 5(5): 952-955.

NIU Wenjie, YE Weimin, CHEN Bao, et al. SWCC and permeability of unsaturated Gaomiaozi bentonite in free swelling condition[J]. Chinese Journal of Underground Space and Engineering, 2009, 5(5): 952-955.

[24] WERSIN P. Geochemical modelling of bentonite pore water in high-level waste repositories[J]. Journal of Contaminant Hydrology, 2003, 61(1/2/3/4): 405-422.

（编辑 赵俊）

收稿日期： 2018 -10 -08; 修回日期： 2018 -12 -03

基金项目(Foundation item)：国家自然科学基金资助项目(41630633)(Project(41630633) supported by the National Natural Science Foundation of China)

通信作者：徐永福，博士，教授，从事分形介质力学、非饱和(特殊)土力学理论和地基处理研究；E-mail：yongfuxu@sjtu.edu.cn