文章编号：1004-0609(2014)05-1259-09

基于正交切削理论的航空钛合金切削加工本构模型构建

杨  勇，朱卫卫，李  明

(青岛理工大学 机械工程学院，青岛 266033)

摘  要：为弥补现有航空钛合金切削加工本构模型研究的不足，提出基于正交切削理论的材料本构模型构建方法。根据正交切削理论建立剪切区内应力、应变、应变率、温度以及二维切削力的数学模型，开发以剪切区长度和厚度比值为迭代变量的建模技术，结合动态压缩力学性能实验(SHPB实验)和直角铣削实验，通过对各变形参数的数学求解，建立航空钛合金切削加工本构模型。在此基础上，进行材料本构模型的分析和实验验证。结果表明：航空钛合金材料在切削加工中具有明显的应变硬化特性、温度敏感特性和应变率敏感特性；钛合金随着应变率的增大，流动应力的增量逐渐减小，材料的应变率敏感性降低。

关键词：钛合金；切削加工；正交切削理论；本构模型

中图分类号：TG146　　     文献标志码：A

Construction of material constitutive model during cutting process for aeronautical titanium alloy based on orthogonal cutting theory

YANG Yong, ZHU Wei-wei, LI Ming

(School of Mechanical Engineering, Qingdao Technological University, Qingdao 266033, China)

Abstract: To make up the shortcoming of the current researches in material constitutive model during cutting process, a construction method of material constitutive model based on orthogonal cutting theory was presented. According to the orthonal cutting theory, the mathematic model of stress, strain, strain rate and temperature in shear zone, as well as the two-dimensional cutting force, was established. The constrution technology of material constitutive model by taking the ratio of length to depth in shear zone as an iterative variable was developed. With the split Hopkinson pressure bar (SHPB) compression experiment and orthogonal cutting experiment, the material deformation physical quantities were solved and the material constitutive model was established. The prediction values of material constitutive model were compared with the cutting experiment ones, and they are found to be in good agreement. The results show that titanium alloy material has obvious strain hardening characteristic, temperature sensitivity characteristic and strain rate sensitivity characteristic during cutting process. And with the increase of strain rate, the flow stress increment decreases, and the strain rate sensitivity characteristic decreases.

Key words: titanium alloy; cutting process; orthogonal cutting theory; constitutive model

材料本构模型用来描述材料的力学性质，表征材料变形过程中的动态响应。建立材料本构模型，不管是在制定合理的加工工艺方面，还是在金属塑性变形理论的研究方面都极其重要。切削加工力学是现代力学的一个分支，加工过程中材料发生的剧烈变形是一个典型的塑性变形力学问题，因而，材料本构模型的建立也是金属切削研究领域密切关注的问题。

当前，针对切削加工工艺的材料本构模型研究还较少，已有的工作主要是通过动态压缩实验(SHPB实验)和拉伸实验建立材料本构模型。TIAN等^[1]通过不同温度下的压缩和拉伸实验建立了铝合金5A02的本构模型，并进一步分析了高应变率影响材料动态力学行为的机理；MOHOTTI等^[2]通过高应变率拉伸实验建立了聚脲的本构模型，研究了该种材料的高应变率行为，结果表明聚脲具有高应变率敏感；LIN等^[3]利用单轴拉伸实验建立了Al-Cu-Mg合金的材料本构模型，研究结果显示真应力-应变曲线在很小的应变下出现峰值，其后流动应力逐渐降低；LEE等^[4]利用SHPB实验建立了钛合金Ti-6Al-4V的本构模型，实验中应变率为2000 s^-1，温度为1100 ℃；MEYER等^[5]采用SHPB实验研究了钛合金Ti-6Al-4V的本构模型，实验中应变率为2150 s^-1；DIPTI等^[6]利用等温热压缩实验数据建立了钢9Cr-1Mo的Johnson-Cook本构模型，实验中应变范围为0.1~0.5，应变率范围为0.001~ 1 s^-1；JASPERS等^[7]通过SHPB实验建立了钢1045和铝合金6082-T6的本构模型，研究了其高温变形行为；李莎等^[8]建立了新型镍基高温合金GH4700的热变形本构模型，研究了合金的热变形行为和组织演变，结果表明合金的流变应力随着应变速率的减小和变形温度的升高而降低；杨春晖等^[9]利用高温压缩实验建立了Ti-6Al-4V合金的高温变形本构模型，构建了Ti-6Al-4V 合金的应力-应变曲线，并分析了应变率和应变温度对流动应力的影响；李红斌等^[10]利用压缩实验构建了带有温度补偿的材料本构模型，研究了热压缩变形过程中塑性功转化热造成的温度升高对构建材料本构模型精确度的影响，结果表明由塑性功转化热造成的温升与真应变呈线性关系；黄志刚^[11]和成群林^[12]分别通过拉伸实验和SHPB实验建立了7075和7050铝合金的本构模型，用于切削加工数值模拟研究；鲁世红等^[13]利用SHPB实验测试了钛合金TC4的动态力学性能数据，并进一步通过自适应遗传算法(GA)优化建立了适合切削加工模拟的本构模型。而有关研究表明：压缩和拉伸实验中(特别是对于较硬的金属材料)应变远小于1，应变率小于1×10³ s^-1，而切削加工工艺中应变在1左右，应变率在1×10⁴~1×10⁶ s^-1之间，高速切削加工应变和应变率会更大^[14]。一般将切削加工中的材料本构问题称为具有大应变、高应变率和高温等特征的本构问题。由于材料的力学性能与应变、应变率和温度密切相关，在大应变和高应变率、高温情况下材料性能发生了较大的变化，如屈服极限和强度极限上升，伸长率下降，使材料呈脆性，出现应变率硬化效应^[15]。因此，材料在切削加工过程中的力学性能与拉伸、压缩实验条件下表现出的力学性能截然不同，上述通过拉伸、压缩实验数据拟合得到的材料本构模型不能用于切削加工材料性能的预报。

综合前期研究，尽管国内外学者对该问题进行了大量研究，但所建立的材料本构模型仍难以令人满意。本文作者以在航空航天工业中应用越来越广泛的钛合金TC4材料为研究对象，提出了基于正交切削理论的材料本构模型构建方法，结合动态压缩力学性能实验和直角铣削实验，通过对各变形参数的数学求解，建立了航空钛合金TC4材料本构模型，为预测钛合金材料性能和进行切削加工数值模拟研究奠定基础。

1  建模方法

1.1  应力场、应变场、应变率场和温度场的建立

在金属切削理论中，OXLEY^[16]提出了可以广泛概括从低速切削至高速切削试验结果的切削理论，该理论中引入了加工硬化概念，并且考虑了剪切区的宽度，本文作者利用该切削理论进一步推导切削区内物理量的数学表达式。OXLEY切削理论中的模型示意图如图1所示。图中p_A和p_B为作用在剪切面AB两端的静水压力，h为剪切区厚度。

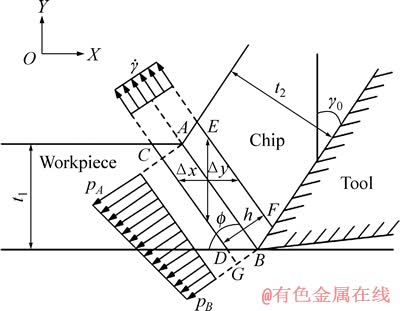
图1  金属正交切削模型示意图

Fig. 1  Schematic diagram of metal orthogonal cutting model

工件经过始剪切滑移线CD进入剪切区，发生剪切滑移，越过终剪切滑移线EF成为切屑而被去除。在CD线上任取一质点M，针对该质点建立其在剪切区中的应变率、应变、应力和温度等各物理量数学关系式。图中，AB、CD、EF相互平行，它们是最大剪切应力方向同时也是最大剪切面应变速度方向，因为考虑的是单纯剪切变形，所以剪切区内的剪切应变率可以取为最大剪切应变速度区域的平均值。即

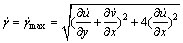                (1)

式中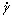：为剪切面AB上的平均应变率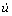，和分别为质点在x和y方向的速度。

正交切削过程中速度关系如图2所示。图中v为削速度；v_c为切屑速度；v_s为剪切速度。

图2  正交切削过程中的速度关系

Fig. 2  Velocity relation in orthogonal cutting process

剪切角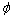通过式(2)求解：

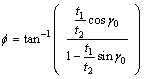                      (2)

式中：t₁为切削厚度，t₂为切屑厚度，为刀具前角。

剪切面AB上的平均剪切应变率()为

                           (3)

式中：v为切削速度，h为剪切区厚度。

剪切面AB上的应变是平均剪切应变率与质点通过剪切区的时间的乘积，因此，

                       (4)

式中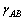：为剪切面AB上的平均剪切应变。

根据正交切削的力学关系可得：

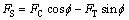                        (5)

式中：F_S为剪切面AB上的剪切力，F_C为切削分力，F_T为进给分力。

根据式(5)可得平均剪切应力(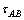)为

                               (6)

式中：w为切削宽度，在直角铣削试验中相当于轴向铣削深度。

根据OXLEY切削理论，剪切面AB上的平均切削温度可表示为

                             (7)

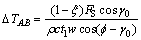                      (8)

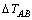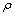式中：T₀为工件初始温度，为温度增量，为切削热传入工件的比例因子，为工件材料密度，c为工件材料的比热容。

其中：

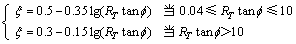(9)

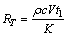
式中：K为工件材料的热传导系数。

1.2  二维切削力预测

正交切削模型中切削力的平衡系如图3所示^[17]。图中，R′为剪切面上切削合力，R为前刀面上切削合力，F为前刀面摩擦力，N为前刀面法向力，F_N为剪切面法向力，β为刀具前刀面上的平均摩擦角。

剪切面AB上法向力可以表示为

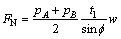                       (10)

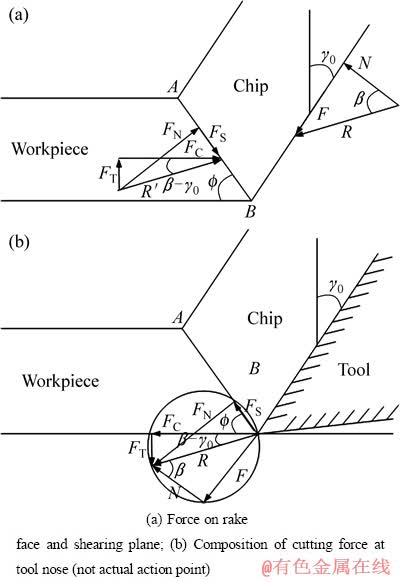
图3  切削力的平衡系

Fig. 3  Equilibrium system of cutting force

剪切面AB上的剪切力可以表示为

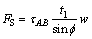                            (11)

设合力R与剪切面AB夹角为θ，则有：

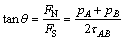                        (12)

剪切面AB端点A处压力为

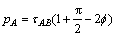                         (13)

根据切削理论可得到^[18]：

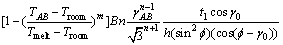(14)

将式(13)和(14)代入式(12)得：

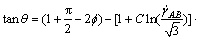
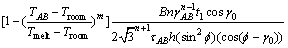(15)

从图3中根据几何关系可得到合力R：

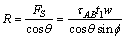                       (16)

继而得到正交切削过程中的切削分力和进给分力：

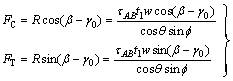       (17)

1.3  本构模型构建方法

从以上剪切面上平均应变率、应变、应力和温度物理量的计算过程可以看出，它们与切削分力、进给分力、切屑厚度以及剪切区厚度密切相关，切削分力、进给分力和切屑厚度可以通过直角切削试验获得。前期研究得出，剪切区长度和厚度之比是个变量，随工件材料和切削条件而变，其值在6~12范围内变动^[18]。设剪切区长度和厚度之比为l，其数学形式描述如下：

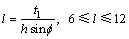                       (18)

式中：t₁为切削厚度，h为剪切区厚度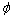，为剪切角。

基于剪切区长度和厚度之比在某一范围内变化这一特性，以剪切区长度和厚度的比值为迭代变量，由迭代变量的初始值计算出切削力的理论值，再通过切削力理论值和实验值的比较不断修正迭代变量，使切削力理论值和实验值相差很小，最终获得该范围内较为合理的变量值l，进而通过l值建立合理的本构模型。由此形成基于正交切削理论的材料本构模型建模方法，建模技术路线如图4所示。

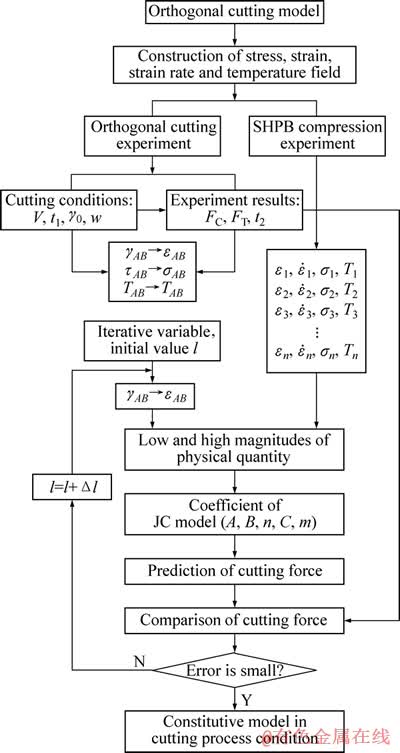
图4  基于正交切削理论的材料本构模型构建技术路线

Fig. 4  Technological route of construction of material constitutive model based on orthogonal cutting theory

2  辅助实验

2.1  动态压缩力学性能实验(SHPB实验)

利用SHPB实验获取钛合金材料在一般动态情况下的应力、应变、应变率和温度物理量数据，为建立能够充分描述切削加工过程材料力学特性变化的本构模型提供低数量级的物理量数据。SHPB实验测试系统如图5所示。

根据SHPB实验条件和钛合金TC4的硬度情况，实验中最高温度设计为800 ℃，最高应变率设计为8000 s^-1。实验中所采用的试样分为3种，准静态压缩时采用长度和直径均为9 mm的试样，动态压缩低应变率下采用长度和直径均为5 mm的试样，高应变率下采用直径和长度仅为2 mm的试样。为保证实验测试结果的可靠性，试样两端面的平行度、平面度和表面粗糙度等均作了严格处理。

2.2  直角铣削实验

结合切削加工特征，根据正交切削力学特性设计了直角铣削实验，为基于正交切削理论的材料本构建模方法提供切削分力、进给分力以及切屑厚度等正交铣削数据。

直角铣削实验装置包括试件底座、试件和刀具3个部分。试件底座使用铸铁材料制成，设计成双排铣槽，端面尺寸和测力仪相配，底座下端面平行度、平面度和表面粗糙度等按照实验要求作严格处理。试件设计成薄板，尺寸和试件底座上端面一致。刀具主切削刃设计成直线形，直径为16 mm，2齿，材料为硬质合金，由刀具制造商专门制作。试件用螺栓固定在试件底座上，底座和测试仪器相连，刀具在铣槽中作直线运动，整个实验装置放在机床工作台上进行铣削实验。实验装置如图6所示。

3  本构模型建立

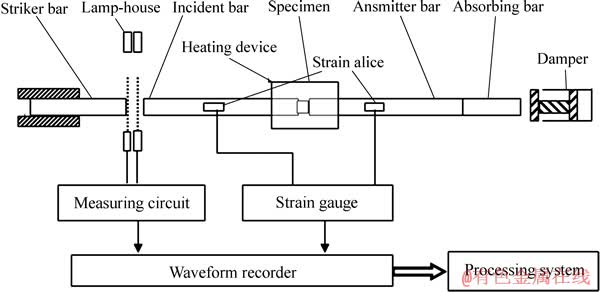
图5  SHPB实验测试系统示意图

Fig. 5  Diagram of SHPB testing system

图6  实验装置设计图

Fig. 6  Experiment device design

当前常用的材料本构模型主要有：Johnson-Cook模型、Bodner-Paton模型、Follansbee-Kocks模型、Zerrilli-Armstrong模型^[19-22]等。其中，Johnson-Cook (简称JC模型) 本构模型引入了材料的应变硬化、应变率强化及热软化参数，综合反映了大应变、高应变率和高温加载下金属的本构关系，对不同材料的适用性较好，同时它自身形式简单，所使用的变量适用于多种计算机编码，是一个可应用于分析计算的实用模型，本文作者以该模型作为钛合金切削加工中的材料本构方程式。Johnson-Cook材料本构模型的数学方程式表示如下：

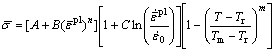(19)

式中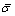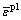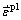：、、分别为应力、等效塑性应变、等效塑性应变率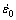；为参考应变率；A、B、C、n、m为材料常数；T_m、T_r、T分别为材料的熔点、参考温度、材料温度。

利用由直角铣削实验和SHPB实验得到的应力、应变、应变率和温度数据，对Johnson-Cook本构模型进行非线性回归分析，确定该本构模型中的常数，分析过程在大型仿真软件Matlab中进行。最后根据材料本构模型建模技术路线得到钛合金TC4材料Johnson-Cook本构模型的具体方程式为

                       (20)

式中：钛合金熔点为1560 ℃，参考温度为20 ℃，应变范围为0~0.73，应变率范围为0.001~41043 s^-1，温度范围为20~872 ℃。

将Johnson-Cook本构模型中参数范围和SHPB实验中参数范围比较，可以得出，Johnson-Cook本构模型中参数范围大于SHPB实验中参数范围，特别是在应变和应变率参数方面，Johnson-Cook本构模型有了较大的扩展。同时和文献[14]给出的切削加工条件下产生的变形参数范围比较，可以得知，Johnson-Cook本构模型中参数范围在切削加工条件下产生的变形参数范围之内。由此说明，Johnson-Cook本构模型可以应用到切削加工领域，所建立的钛合金TC4材料本构模型能够体现切削加工中的大应变、高应变率和高温特征。

4  本构模型分析和验证

4.1  本构模型分析

4.1.1  相同应变率、不同温度下的应力－应变关系曲线分析

根据模型绘制相同应变率不同温度下的应力－应变关系曲线，结果分别如图7~9所示。

图7  应变率为1000 s^-1时JC模型预测的应力-应变曲线

Fig. 7  Predicting stress-strain curves of JC model at strain rate 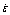=1000 s^-1

图8  应变率为5000 s^-1时的JC模型预测应力-应变曲线

Fig. 8  Predicting stress-strain curves of JC model at strain rate 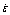=5000 s^-1

图9  应变率为10000 s^-1时的JC模型预测应力-应变曲线

Fig. 9  Predicting stress-strain curves of JC model at strain rate 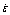=10000 s^-1

通过比较和分析以上曲线，得出材料本构模型表现出的力学特性如下：1) 材料有明显的应变硬化特性，即流动应力随应变的增加而逐渐增大；2) 材料具有明显的温度敏感性，即随着温度的升高，流动应力逐渐降低，这种现象即是材料的温度软化效应。

4.1.2  相同温度、不同应变率下的应力－应变关系曲线分析

根据大应变材料本构模型绘制相同温度不同应变率下的应力－应变关系曲线，结果分别如图10~13所示。

通过比较和分析以上曲线，得出材料本构模型表现出的力学特性如下：1) 材料有明显的应变硬化特性，即流动应力随应变的增加而逐渐增大；2) 材料具有明显的应变率敏感性，即随着应变率的增大，流动应力逐渐增大，这种现象即是材料的应变率强化效应；3) 随着应变率的增大，流动应力的增量逐渐减小，材料的应变率敏感性降低，这主要是高速变形情况下，温度升高，其软化作用大于应变率的强化作用，减小了流动应力的增长程度，导致应变率的敏感性降低。

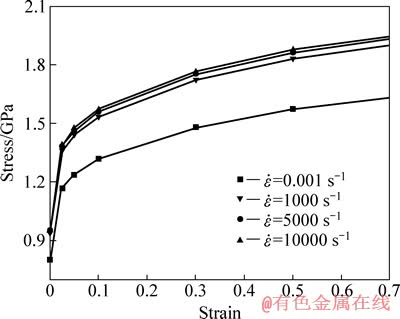
图10  温度为20 ℃时的JC模型预测应力-应变曲线

Fig. 10  Predicting stress-strain curves of JC model at temperature of 20 ℃

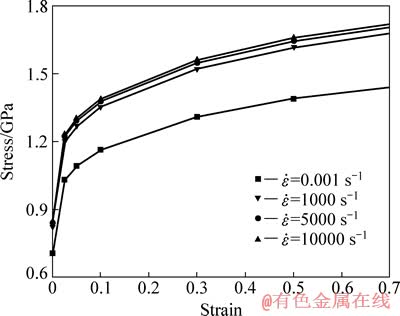
图11  温度为200 ℃时的JC模型预测应力-应变曲线

Fig. 11  Predicting stress-strain curves of JC model at temperature of 200 ℃

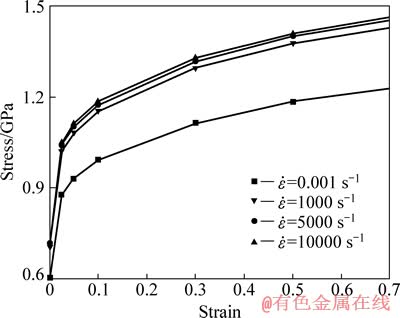
图12  温度为400 ℃时的JC模型预测应力-应变曲线

Fig. 12  Predicting stress-strain curves of JC model at temperature of 400 ℃

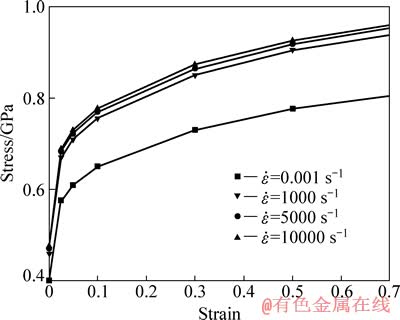
图13  温度为800 ℃时的JC模型预测应力-应变曲线

Fig. 13  Predicting stress-strain curves of JC model at temperature of 800 ℃

众所周知，应变率和温度对材料的力学性能有明显的影响，随着应变率的增加，材料的屈服强度和流动应力都会提高，随着温度的升高，材料的屈服强度和流动应力将会降低。通过上述对不同温度和应变率下的应力－应变关系曲线分析可以看出，本文作者所建立的材料本构模型很好地体现了这两个材料特性。

4.2  本构模型验证

为了验证钛合金TC4材料本构模型预测值的准确性，分别抽选10组SHPB实验数据和由直角铣削实验结果计算得到的变形参数数据与本构模型的预测值进行比较，比较结果如表1和2所列。

表1  JC本构模型预测值与SHPB实验测量值比较

Table 1  Comparisons between predicting values of JC model and SHPB testing values

表2  JC本构模型预测值与直角铣削实验值比较

Table 2  Comparisons between predicting values and orthogonal milling experiment values

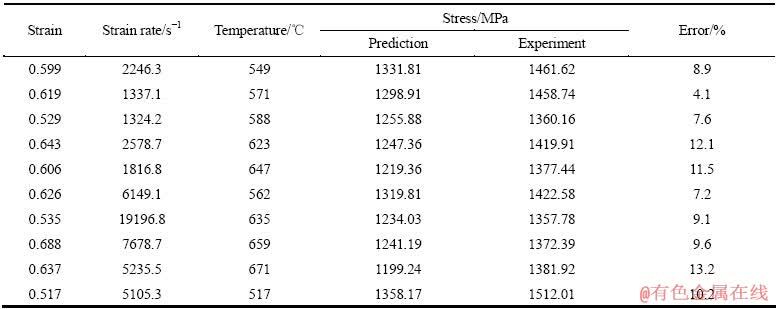
从两表中可以看出，模型预测值和SHPB实验值的平均误差为14.3%，其中最大误差为18.7%，模型预测值和直角铣削实验结果计算值的平均误差为9.35%，其中最大误差为13.2%，材料本构模型预测值与由直角铣削实验结果计算得到的变形参数数据吻合较好，表明所建立的钛合金本构模型较为合理，该模型能够正确描述切削加工中材料的大应变、高应变率和高温等“三高”特征。

5  结论

1) 面向工程应用，提出了基于正交切削理论的钛合金材料本构模型建模方法。根据正交金属切削理论建立了剪切区内应力、应变、应变率、温度以及二维切削力的数学模型，开发了以剪切区长度和厚度比值为迭代变量的建模技术，结合动态压缩力学性能实验和直角铣削实验，通过对各变形参数的数学求解，建立了航空钛合金TC4材料本构模型。材料本构模型预测值与由直角铣削实验结果计算得到的变形参数数据吻合较好，表明所建立的钛合金本构模型较为合理。

2) 根据所建立的航空钛合金材料本构模型绘制不同温度和应变率下的应力－应变关系曲线，分析得出：钛合金材料具有明显的应变硬化特性、温度敏感特性和应变率敏感特性，即流动应力随应变的增加逐渐增大，随着温度的升高逐渐降低，随着应变率的增大逐渐增大；钛合金材料随着应变率的增大，流动应力的增量逐渐减小，材料的应变率敏感性降低。

3) 本文作者建立的材料本构模型扩展了SHPB实验数据拟合模型中的应变、应变率和温度范围，能够应用到切削加工领域，为进一步开展切削加工中的材料性能预测以及进行切削加工数值模拟研究奠定了基础。

REFERENCES

[1] TIAN Y, HUANG L, MA H J, LI J J. Establishment and comparison of four constitutive models of 5A02 aluminium alloy in high-velocity forming process[J]. Materials and Design, 2014, 54: 587-597.

[2] MOHOTTI D, ALI M, NGO T, LU J H, MENDIS P. Strain rate dependent constitutive model for predicting the material behaviour of polyurea under high strain rate tensile loading[J]. Materials and Design, 2014, 53: 830-837.

[3] LIN Y C, DING Y, CHEN M S, DENG J. A new phenomenological constitutive model for hot tensile deformation behaviors of a typical Al-Cu-Mg alloy[J]. Materials and Design, 2013, 52: 118-127.

[4] LEE W S, LIN C F. High-temperature deformation behavior of Ti6AL4V alloy evaluated by high strain-rate compression tests [J]. J Mater Process Technol, 1998, 75: 127-136.

[5] MEYER H W, KLEPONIS D S. Modeling the high strain rate behavior of titanium undergoing ballistic impact and penetration[J]. Int J Impact Eng, 2001, 26: 509-521.

[6] DIPTI S, SUMANTRA M, BHADURI A K. A comparative study on Johnson-Cook, modified Zerilli-Armstrong and Arrhenius-type constitutive models to predict elevated temperature flow behaviour in modified 9Cr-1Mo steel[J]. Computational Materials Science, 2009, 47: 568-576.

[7] JASPERS S P F C, DAUTZENBERG J H. Material behavior in conditions similar to metal cutting: Flow stress in the primary shear zone[J]. J Mater Process Technol, 2002, 122: 322-330.

[8] 李 莎, 苗华军, 金宪哲, 郝文慧. 新型镍基高温合金GH4700热变形行为及组织演变研究[J]. 铸造技术, 2013, 34(8): 953-957.

LI Sha, MIAO Hua-jun, JIN Xian-zhe, HAO Wen-hui. Research on hot deformation behavior and microstructure evolution of new nickel-based superalloy GH4700[J]. Foundry Technology, 2013, 34(8): 953-957.

[9] 杨春晖, 王 举, 李 楠. 基于Ti-6Al-4V合金高温变形建立的本构方程[J]. 计量与测试技术, 2013, 40(9): 6-8.

YANG Chun-hui, WANG Ju, LI Nan. Constitutive equation of deformation for Ti-6Al-4V alloy in high temperature[J]. Measurement and Testing Technology, 2013, 40(9): 6-8.

[10] 李红斌, 方 芳, 刘珊珊, 徐树成. 基于Gleeble 快速压缩试验构建材料本构方程的研究[J]. 热加工工艺, 2013, 42(22): 51-54.

LI Hong-bin, FANG Fang, LIU Shan-shan, XU Shu-cheng. Study on construction of material’s constitutive equation based on gleeble fast compression test[J]. Hot Working Technology, 2013, 42(22): 51-54.

[11] 黄志刚. 航空结构件铣削加工变形的有限元模拟及其关键技术研究[D]. 杭州: 浙江大学, 2003.

HUANG Zhi-gang. Study on finite element simulation of distortion due to milling process and key technologies for aerospace monolithic component[D]. Hangzhou: Zhejiang University, 2003.

[12] 成群林. 航空整体结构件切削加工过程的数值模拟与实验研究[D]. 杭州: 浙江大学, 2006.

CHENG Qun-lin. Study on numerical simulation and experiment of machining process for aerospace monolithic components[D]. Hangzhou: Zhejiang University, 2006.

[13] 鲁世红, 何 宁. TC4钛合金动态本构模型与高速切削有限元模拟[J]. 兵器材料科学与工程, 2009, 32(1): 5-9.

LU Shi-hong, HE Ning. Dynamic constitutive model of titanium alloy TC4 and finite element simulation of high-speed cutting[J]. Ordnance Material Science and Engineering, 2009, 32(1): 5-9.

[14] MAHMOUD S, CHRISTIAN K, ALTAN T. Process modeling in machining. PartⅠ: Determination of flow stress data[J]. International Journal of Machine Tools ＆ Manufacture, 2001, 41: 1511-1534.

[15] 金树达, 朱东升. 材料力学[M]. 北京: 冶金工业出版社, 1996.

JIN Shu-da, ZHU Dong-sheng. Material mechanics[M]. Beijing: Metallurgical Industry Press, 1996.

[16] OXLEY P L B. Mechanics of machining, an analytical approach to assessing machinability[M]. Ellis Horwood Limited, 1989.

[17] JASPERS S P F C, DAUTZENBERG J H. Material behavior in metal cutting: Strains, strain rates, and temperatures in chip formation[J]. J Mater Process Technol, 2002, 121(1): 123-135.

[18] JIU-JING Y Z. 切削磨削加工学[M]. 高希正, 刘德忠, 译. 北京: 机械工业出版社, 1982.

JIU-JING Y Z. Machining theory of cutting and grinding[M]. GAO Xi-zheng, LIU De-zhong, tranls. Beijing: China Machine Press, 1982.

[19] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strain rates and high temperatures[C]//Proceedings of the 7th International Symposium on Ballistics. Netherlands, 1983.

[20] ZERILLI F J, ARMSTRONG R W. Dislocation mechanics based constitutive relations for material dynamics calculations[J]. Journal of Applied Physics, 1987, 61(5): 1816-1825.

[21] ZHOU M, NEEDLEMAN A, CLIFTON R J. Finite element simulations of dynamic shear location [J]. J Mech Phys Solids, 1994, 42: 423-458.

[22] CLIFTON R J. Dynamic plasticity[J]. Journal of Applied Mechanics, 1983, 50: 941-952.

(编辑  龙怀中)

基金项目：国家自然科学基金资助项目(51105216)；山东省优秀中青年科学家科研奖励基金资助项目(BS2011ZZ006)

收稿日期：2013-06-13；修订日期：2013-12-16

通信作者：杨  勇，副教授，博士；电话：0532-85071286；E-mall：yangyong913@gmail.com