J. Cent. South Univ. Technol. (2008) 15(s1): 043-046
DOI: 10.1007/s11771-008-311-5
Constitutive model depending upon temperature and strain rate of carbon constructional quality steels
YANG Liu(杨 柳)1, LUO Ying-she(罗迎社)2
(1. School of Landscape Architecture, Zhejiang Forestry University, Hangzhou 311300, China;
2. Institute of Rheological Mechanics and Material Engineering,
Central South University of Forestry and Technology, Changsha 410004, China)
Abstract: The basic factors relating to the rheological stress in the constitutive equations were introduced. Carbon constructional quality steels were regarded as a kind of elastic-viscoplastic materials under high temperature and the elastic-viscoplastic constitutive models were summarized. A series of tension experiments under the same temperature and different strain rates, and the same strain rate and different temperatures were done on 20 steel, 35 steel and 45 steel. 52 groups of rheological stress—strain curves were obtained. The experimental results were analyzed theoretically. The rheological stress constitutive models of carbon steels were built combining the strong points of the Perzyna model and Johnson-Cook model. Comparing the calculation results conducted from the model with the experiment results, the results proves that the model can reflect the temperature effect and strain rate effect of carbon constructional quality steels better.
Key words: rheological stress; strain rate effect; temperature effect; constitutive model
1 Introduction
Recently, with the rapid development of computer technology and the gradual advancement of numerical method, semi-analytical numerical method, the finite element modeling technology has become the most practical and convenient way. In order to achieve the numerical simulation calculating rheological forming process of materials, it is necessary to find the constitutive equations, by which the rheological properties of materials under hot-working condition are described more accurately. As the rheological constitutive models of materials presented by far are not all applicable, it is the most widely used method to establish the related rheological model that collects abundant stress datum under certain strain rates and temperature by experiments. CLAUSEN et al[1] used the two modified Johnson-Cook models describing flow stress and fracture strain of aluminium alloy AA5083-H116 based on a great deal of tests under different strain rates, temperatures and triaxialities. LEE and YEH[2] investigated the deformation behavior of AISI 4340 alloy steel under high strain rates ranging from 500 to 3 300 s-1 and at constant temperature in the range of 20-1 100 ℃ by means of a split Hopkinson bar. KOZLOWSKI and ANAND[3] proposed one- dimensional analytical models to describe the response of plain carbon steel at high temperature and low strain rate using the experimental data set of Wray. HUESPE[4] described the flow stress and strain of steel under high temperature with Anand model and Chaboche model, taking hardening effect, creep and other factors into account. KHAN and LIANG[5] studied the behaviors of three BCC metal over a wide range of strain rates and temperature and proposed a new constitutive model. LUBARDA et al[6] investigated the strain rate effects in rheological models of inelastic response. LUO et al[7] studied the tesile rheological properties of sheet Tc1T- alloy under different temperatures and strain rates.
In this work, a series of tensile experiments under the same temperature and different strain rates, under the same strain rate and different temperatures were done on the carbon construction quality steels, such as 20 steel, 35 steel and 45 steel. 52 groups of rheological stress-strain curves were obtained. The experimental results were analyzed theoretically. Furthermore, the rheological stress constitutive models of carbon steels were built combining the strong points of the Perzyna model and Johnson-Cook model(more simply JC model).
2 Experimental
The experimental facilities included Shimadzu Autograph electric universal testing machine (AG-1) and a computer. The instrument can perform tensile /compression/torsion tests under certain temperatures. It also has the functions of controlling the strain and stress. The experimental materials were 20 steel, 35 steel and 45 steel. The heat treatment was normalizing. The samples used in the tests were dog-bone specimens with gauge length of 30 mm and cross-sectional diameter of 5 mm after normalized treatment.
The experimental schemes are as follows: A series of tensile tests under lower strain rates in the range of 10-4-10-1/s and at constant temperatures in the range of 20-500 ℃ were done on the 20 steel. 16 groups of strain-stress curves were obtained and theoretical analyses were done on the results. Tensile tests under three kinds of temperature(450, 500, 550 ℃) and under four kinds of strain rates(0.05, 0.1, 0.15, 0.2/s) were performed on 20 steel, 35 steel and 45 steel, respectively. 36 groups of strain-stress curves were obtained. The constitutive relationship of carbon constructional quality steel under higher temperatures and different strain rates were studied.
Figs.1 and 2 present the strain—stress curves at different strain rates at 20 ℃ and 500 ℃, respectively. The yield limit and rheological stress of 20 steel increase with the strain rate, and it is not very distinct at room temperature while it is obvious at high temperature. We can conclude from Figs.1 and 2 that at higher temperatures the strain rate is the key factor that influences the rheological stresses and at lower strain rates the temperature is the key factor. It demonstrates that the material of 20 steel appears work hardening, recovery and recrystallization in the thermo-tensile processes.
Fig.3 presents the stress-strain curves of tension of 20 steel at 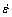 =0.2/s. Fig.4 presents the stress—strain
=0.2/s. Fig.4 presents the stress—strain
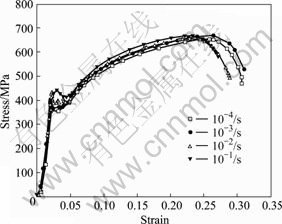
Fig.1 σ-ε curves of elongation of 20 steel at 20 ℃
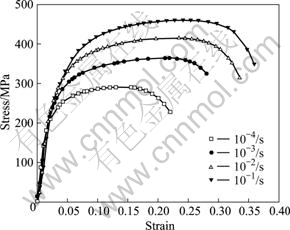
Fig.2 σ-ε curves of elongation of 20 steel at 500 ℃
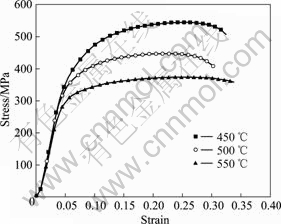
Fig.3 σ-ε curves of tension of 20 steel at 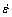 =0.2/s
=0.2/s
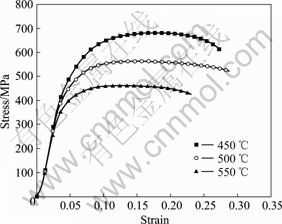
Fig.4 σ-ε curves of tension of 35 steel at 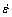 =0.15/s
=0.15/s
curves of tension of 35 steel at 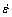 =0.15/s. Fig.5 presents the stress—strain curves of elongation of 45 steel at 550 ℃. It can be concluded from these experimental charts that the rheological stresses of carbon constructional quality steels are very sensitive to strain rate and temperature. Yield stress and rheological stress increases with the increase of strain rate and decreases with the increase of temperatures, which show remarkable strain rate hardening and temperature soften effect.
=0.15/s. Fig.5 presents the stress—strain curves of elongation of 45 steel at 550 ℃. It can be concluded from these experimental charts that the rheological stresses of carbon constructional quality steels are very sensitive to strain rate and temperature. Yield stress and rheological stress increases with the increase of strain rate and decreases with the increase of temperatures, which show remarkable strain rate hardening and temperature soften effect.
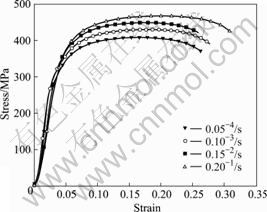
Fig.5 σ-ε curves of elongation of 45 steel at 550 ℃
3 Determination on nonlinear viscoplastic constitutive equations
According to the tensile curves, it can be seen that strain rates have great influence on yield limits of carbon steels, so the carbon steel can be called strain rate sensitive materials[8]. The rigid-viscoplastic constitutive model developed by PERZYNA[9] is a relatively comprehensive model, which not only reflects the plastic properties of material but also includes the nonlinear properties of rate sensitive. Unfortunately, the work hardening effect and temperature softening effect were not considered in this model and temperature was not expressed in the equations. JOHSON and COOK[10] presented a new viscoplastic empirical model (JC model in short). This model can depict the effects of strain hardening, strain rate sensitivities and temperature soften. Although the JC strength model is empirical in nature and simple in form, it is the most popular strength model in use today.
Perzyna’s overstress model is described as follows:
 (1)
(1)
where σs is the yield strength under simple axial tension; 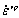 is the viscoplastic strain rate; γ* is the materials coefficient of viscosity property which can be determined by experiment[11] and n is a empirical exponent.
is the viscoplastic strain rate; γ* is the materials coefficient of viscosity property which can be determined by experiment[11] and n is a empirical exponent.
JC model has the following form:
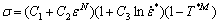 (2)
(2)
where σ is the equivalent yield strength; ε is the equivalent plastic strain; 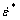 is the dimensionless equivalent plastic strain rate(made dimensionless by dividing the equivalent plastic strain by a unit plastic strain rate); T* = (T - Tr)/(Tm - Tr) is a dimension-less temperature; Tr is room temperature and Tm is melting temperature; Ci, N and M are material constants determined by limited straining tests done in tension or torsion.
is the dimensionless equivalent plastic strain rate(made dimensionless by dividing the equivalent plastic strain by a unit plastic strain rate); T* = (T - Tr)/(Tm - Tr) is a dimension-less temperature; Tr is room temperature and Tm is melting temperature; Ci, N and M are material constants determined by limited straining tests done in tension or torsion.
The yield function in Perzyna’s over-stress model is independent of strain rate, while Johnson-Cook model does not take metal’s viscosity into consideration, so the merits of these two models were combined and modify the JC model as:
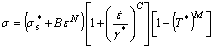 (3)
(3)
The material parameters of equations can be determined as follows:
1) Determining 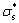 , B and N
, B and N
In equation σ =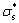 +BεN,
+BεN, 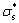 is the yield strength of the material under different temperatures, which can be obtained directly from the σ-ε curves; BεN reflects the hardening portion of σ-ε curves, therefore, the value of B and N can be obtained by the following equation:
is the yield strength of the material under different temperatures, which can be obtained directly from the σ-ε curves; BεN reflects the hardening portion of σ-ε curves, therefore, the value of B and N can be obtained by the following equation:
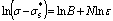 (4)
(4)
2) Determining γ* of certain strain rates and certain temperature based on Perzyna’s overstress model[12]. It can be written as:
 (5)
(5)
where 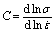 (6)
(6)
3) Temperature effect on tension properties of carbon steels
let Tr=293 K, Tr is the room temperature, the melting point of 20 steel is 1723 K. When T = 723 K, then
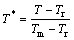 =0.30 (7)
=0.30 (7)
Using the same method, it can be obtained that the values of T* are 0.34 and 0.37 at 773 Kand 823 K, respectively.
4) Using the function of nonlinear fit of software ORIGIN, then determining the rheological stress equations of 20 steel, 35 steel and 45 steel as follows respectively.
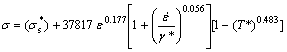 (8)
(8)
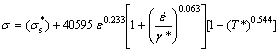 (9)
(9)
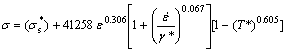 (10)
(10)
Fig.6 shows the comparison of stress—strain curves of elongation between experimental results and calculation results of 20 steel under three kinds of different temperatures. Fig.7 shows the comparison of stress—strain curves of elongation between experimental results and calculation results of 45 steel at temperature 550 ℃ under four kinds of strain rates. It can be seen from Figs.6 and 7, the model can reflect the temperature effect and strain rate effect of carbon constructional quality steels. The model calculation results are in good agreement with the experimental curves, which proves that the model can describe the tensile rheological behavior of carbon steels under higher temperature and strain rate better.
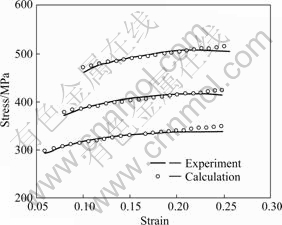
Fig.6 Comparison of σ-ε curves of elongation between experimental results and calculation of 20 steel under different temperatures: 1—450 ℃; 2—500 ℃; 3—550 ℃
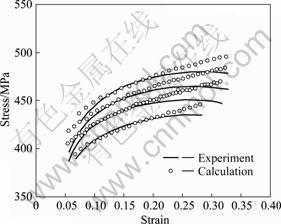
Fig.7 Comparison of σ-ε curves of elongation between experimental results and calculation of 45steel at temperature 550 ℃ under different strain-rates: 1—0.2 /s; 2—0.15 /s; 3—0.1 /s; 4—0.05 /s
4 Conclusions
1) Comparing the two famous visco-plasticity constitutive model Perzyna model and Johnson-Cook model, a modified model reflecting the work-hardening, strain rate effect and viscosity of solid is presented. Temperature is also taken into consideration.
2) The parameters of rheological stress constitutive model of carbon constructional quality steels are determined using the experimental data. Comparing the model calculation with the experimental results, they are in good agreement, which proves the model can describe the constitutive relationship of carbon constructional quality steel better.
References
[1] CLAUSEN A H, BORVIK T, HOPPERSTAD O S, BENALLED A. Flow and fracture characteristics of aluminium alloy AA5083-H116 as function of strain rate, temperature and triaxiality [J]. Journal of Materials Science and Engineering, 2004, 364(1/2): 260-272.
[2] LEE W S, YEH G W. The plastic deformation behaviour of AISI 4340 alloy steel subjected to high temperature and high strain rate loading conditions [J]. Journal of Materials Processing Technology, 1997, 71(2): 224-234.
[3] KOZLOWSKI P F, ANAND L. Simple constitutive equations for steel at high temperature [J]. Metallurgical Transactions A 1992, 23: 903-918.
[4] HUESPE A E, CARFONA A, NIGRO N, FACHINOTTI V. Visco-plastic constitutive models of steel at high temperature [J]. Journal of Materials Processing Technology, 2000, 102(1/3): 143-152.
[5] KHAN A S, LIANG Ri-qiang. Behaviors of three BCC metal over a wide range of strain rates and temperatures. Experiments and modeling [J]. Journal of Plasticity, 1999, 15(10): 1089-1109.
[6] LUBARADA V A, BENSON D J, MEYERS M A. Strain-rate effects in rheological models of inelastic response [J]. Journal of Plasticity, 2003, 19(8): 1097-1118.
[7] LUO Ying-she, TANG Xiao-di, WU Gang. Tensile rheological properties of sheet TC1 Ti-alloy [J]. Journal of Central South University of Technology, 2007, 14(s1): 350-353.
[8] YANG Liu, LUO Ying-she, TANG Xiao-di. Rheological properties of carbon constructional quality steels [J]. Journal of Central South University of Technology, 2007, 14(s1): 285-288.
[9] PERZYNA P. The constitutive equations for rate sensitive plastic materials [J]. Quarterly of Applied Mathematics, 1963, 20: 321-332.
[10] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31-48.
[11] LUO Ying-she, DONDA K, WANG Z, Experimental solution for viscocity coefficient of solid alloy material [J]. Journal of Applied Mechanics and Engineering, 2003, 8: 271-276.
[12] YANG Liu. Research on the constitutive model depending upon temperature and strain rate of carbon constructional quality steels [D]. Xiangtan: Institute of Foundation Mechanics and Material Engineering, Xiangtan University, 2004. (in Chinese)
(Edited by YANG Hua)
Foundation item: Project(2451002035) supported by Zhejiang Forestry University; Project(03JJY3007) supported by the Natural Science Foundations of Hunan Province; Project(02A008) supported by the Education Department of Hunan Province, China
Received date: 2008-06-25; Accepted date: 2008-08-05
Corresponding author: YANG Liu, Master; Tel: +86-13968034169; E-mail: yliu99@163.com