DOI: 10.11817/j.issn.1672-7207.2015.12.007
BR1500HS高强钢与5CrMnMo模具钢的瞬态接触换热系数
夏玉峰,张严东,纪帅
(重庆大学 材料科学与工程学院,重庆,400044)
摘要:利用自制的实验装置,分析热冲压传热过程并将其简化为一维传热,在一定压力和一定的保温时间下测量高强钢和模具的温度变化,基于改进的反传热算法求解在一定界面平均温度和压力以及一定的保温时间下的界面换热系数的变化。研究结果表明:换热系数随着温度和压力的升高而增大且与温度以及压力近似呈幂函数关系,高温时换热系数对压力的敏感性较低温时高。随着保温时间的增加,氧化严重,换热系数减小,且随着压力和保温时间的增加,换热系数逐渐趋于稳定。在一定保温时间下,换热系数只与温度和压力有关,且压力对换热系数的影响较温度对换热系数的影响大,将温度和压力与换热系数很好地拟合在一起,得到换热系数随温度和压力变化的表达式。
关键词:高强钢;模具钢;一维传热;换热系数;反传热算法;温度;压力;氧化
中图分类号:TG113.2 文献标志码:A 文章编号:1672-7207(2015)12-4434-08
Transient contact heat transfer coefficient between high-strength steel BR1500HS and die steel 5CrMnMo
XIA Yufeng, ZHANG Yandong, JI Shuai
(School of Materials Science and Engineering, Chongqing University, Chongqing 400044, China)
Abstract: Based on self-developed experimental apparatus, the process of heat transfer in hot stamping was analyzed and simplified into one dimension heat transfer and the temperature change of high-strength steel and die steel under certain pressure and holding time was measured. The transient contact heat transfer coefficient was calculated at certain mean interface temperature, pressure and holding time by the improved inverse heat transfer algorithm. The results show that the transfer coefficient increases with the increase of temperature and pressure. The load sensitivity at low temperature is less than that at high temperature. The heat transfer coefficient decreases with the increase of holding time due to oxidation. After certain holding time, the heat transfer coefficient is only related to temperature and pressure, and the influence of pressure on heat transfer coefficient is larger than that of temperature on heat transfer coefficient. The temperature and pressure and heat transfer coefficient are fitted together very well. The expression obtains more accurate heat transfer coefficient which changes with temperature and pressure.
Key words: high-strength steel; die steel; one dimension heat transfer; heat transfer coefficient; inverse heat transfer algorithm; temperature; pressure; oxidation
为应对汽车轻量化、高安全性的要求,高强度钢板的热冲压技术在车身制造的领域中受到广泛关注。它是将硼钢板加热至奥氏体化状态后,快速转移到模具中冲压成形,在保证一定的压力情况下以一定的冷却速度进行淬火处理,以获得具有均匀马氏体组织的高强度钢板零件的成形方式。在成形过程中,钢板与模具的接触换热会直接影响成形件内部的温度场,进而影响内部的应力-应变场,并最终影响成形件的性能和寿命。获得准确换热系数对成形过程中的数值模拟、成形工艺的制定和优化起着重要作用。近年来,国内外学者利用不同的方法对不同的材料间的换热系数进行研究,对换热系数的测定和影响因素有了一定的研究成果。然而关于热冲压高强钢和模具之间的换热系数的研究较少,Tondini等[1]通过模拟软件对换热系数进行反分析求解,得出了换热系数是压力的变化函数,但却忽略了温度对换热系数的影响。Hu等[2]运用ABAQUS模拟软件重点研究了高强钢22MnB5氧化作用和压力对H13钢与22MnB5之间随温度变化的换热系数的影响。Bosetti等[3]对比分析了用模拟软件求解和牛顿冷却定律求解2种不同的方法对换热系数的影响,得出了压力对换热系数的影响,同样也忽略了温度对换热系数的影响。以上研究方法大多数为模拟反求解或牛顿冷却定律去分析换热系数的变化,并没有运用瞬态法计算热冲压的换热系数,在热冲压过程中,板料与模具的接触瞬间发生剧烈的热交换,它们之间的传热属于瞬态换热过程。瞬态传热的计算在其他领域的应用也较少。朱智等[4-5]利用自制的瞬态接触换热系数测量装置研究了Hastelloy C-276合金与硅钢间以及TP2铜与3Cr2W8V模具钢之间的瞬态接触换热行为,且温度与热冲压板料的加热温度有所不同。一些瞬态计算过程中将热导率视为常数进行计算,但材料的热导率是随着温度的变化而变化的,热导率的变化对计算结果产生很大影响[6]。很多计算瞬态换热时虽然把过程作为一维传热,但没有模拟验证传热的一维性。目前,BR1500HS高强钢与5CrMnMo模具钢在热冲压过程中的应用越来越广泛,但它们之间的瞬态接触换热过程还未见报道。本文作者依据工业实际生产,采用自制的测量装置对BR1500HS高强钢与5CrMnMo模具钢之间的传热进行一维简化和模拟验证[7],并运用改进的瞬态计算方法对温度和压力以及保温时间对瞬态换热系数的影响进行了研究,从表面形貌的微观机理揭示了换热系数的真实变化,最后对换热系数和温度以及压力进行拟合,为热冲压数值模拟参数的设定和工业实际生产提供了科学依据。
1 实验装置及步骤
选用BR1500HS高强钢切割成直径为80 mm、厚度为1.8 mm的圆片状式样。将5CrMnMo模具钢加工成直径为80 mm、厚度分别为30 mm和20 mm的上下模,上模距离表面0.5,3.0和6.0 mm处分别钻上盲孔安装热电偶用于测各点的温度变化,在下模钻通孔用于测量板料的温度变化。实验用热电偶为k形热电偶,直径为2.5 mm,测温范围为0~1 200 ℃。
实验采用旋压机顶针提供0~10 MPa的压力。采用电阻炉加热,最高温度可达1 200 ℃。用8通道温度记录仪记录各点的温度变化,记录时间间隔为1 s。其实验简化图如图1所示。
本实验分2组,第1组将板料放进加热炉中加热至950 ℃,保温5 min后快速放入模具中以尽量减少热量散失,分别加载1,2,3,4,5和6 MPa。第2组将板料在炉中加热至950 ℃后分别保温2,3,4,5,6,7和8 min取出,在2 MPa压力下,用温度记录仪测量并记录各点的温度变化。
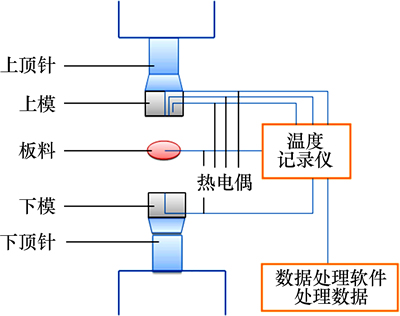
图1 实验装置示意图
Fig. 1 Schematic diagram of experimental apparatus
2 传热的一维简化和模拟验证
由于实验模型是轴对称模型,故取模型的一半来模拟分析传热过程温度的分布。由于该传热过程时间较短,且钢板和模具与空气之间的传热系数较小[7],散热量较少,因此模拟过程中忽略模型与空气的对流换热。模拟过程中,传热系数先设为1 kW/(m2·K),虽然传热系数只是任意设定且随温度变化[7],但不会影响一维传热的模拟分析。钢板最初温度设为860 ℃,模具的最初温度设为室温20 ℃。上模以1 MPa的压强施加于板料上,用有限元分析软件DEFORM-3D模拟传热过程并得到温度的变化曲线和温度场。
模拟过程进行到6 s时,其温度分布如图2和3所示。由于板料较薄,其不同高度的温度分布差异很小。从图2和3可知:板料和模具从中心轴线到边缘的温度基本没有变化,在中心轴线附近的温度分布以及热流只沿着轴线流动,若画一条粗的竖直线,则在竖直线上,温度分布是水平的,可认为热量流动在中心轴线附近只沿着轴线流动,因此在6 s时,热量的流动在板料和模具之间的传热是一维传热。
图4所示为板料表面和距离模具下表面5 mm处0,6和12 s时的温度分布。由图4可以看出:沿着径向,板料和模具在某一时刻的温度分布基本相同,板料的温度在6 s内温度从850 ℃急剧降到600 ℃,模具的温度在6 s内在从室温20 ℃急剧上升至82 ℃,故板料和模具的在这一时间段的传热属于一维传热。
基于以上分析,板料和模具之间的传热可以简化为一维传热。

图2 6 s时板材温度场以及指定点的温度分布
Fig. 2 Temperature field of sheet and distribution of specified points at 6 s
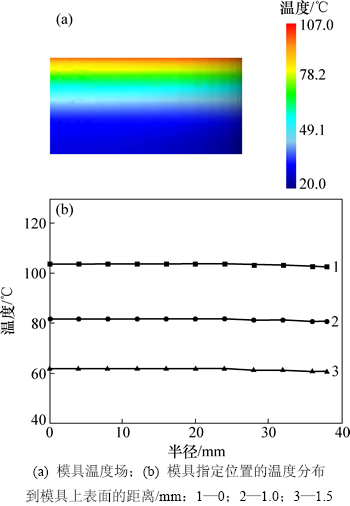
图3 6 s时模具温度场以及指定点的温度分布
Fig. 3 Temperature field of die and distribution of specified points at 6 s
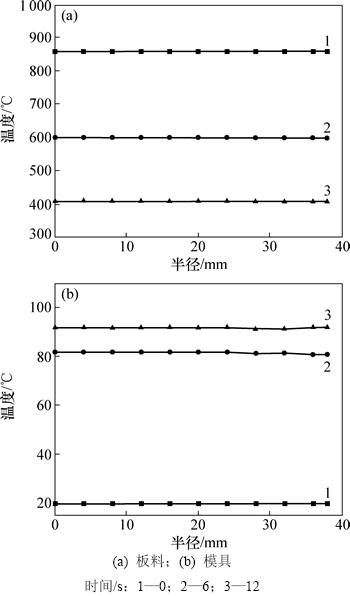
图4 板料和模具的温度变化
Fig. 4 Temperature change of sheet and die
3 反传热问题的求解
反传热问题是根据测得的材料内部温度及其随时间的变化分布,通过求解导热微分方程,得到表面的换热系数以及其他的热物性参数[8]。由前面的分析模拟可知,本实验属于一维传热问题。根据非线性估算方法,建立温度场的控制方程和敏感系数控制方程来求解传热系数,由于材料的热导率随温度变化,本文用改进的反传热算法求解换热系数,把热导率作为温度的函数,对于本实验中高强钢BR1500HS和模具钢5CrMnMo随温度变化的热导率可根据文献[9]和[10]求得,则换热系数的求解过程如下。
温度场的控制方程为
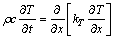 (1)
(1)
其边界条件为
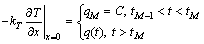 (2)
(2)
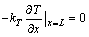 (3)
(3)
其初始条件为
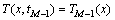 (4)
(4)
式中,C为常数;t为时间;ρ,c和k分别为材料的密度,比热容和热导率,TM-1(x)为tM-1时刻的温度分布,在tM-1和tM之间,热流密度qM为常数,tM-1时的温度分布为已知函数;L为模型的长度,为6 mm。
敏感系数为温度关于热流密度的一阶微商:
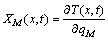 (5)
(5)
敏感系数场的控制方程为
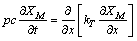 (6)
(6)
其边界条件为
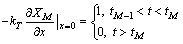 (7)
(7)
 (8)
(8)
其初始条件为
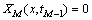 (9)
(9)
敏感系数XM和温度T具有相同形式的微分方程,因此,敏感系数场XM和温度场T都可用有限差分法来计算。
温度场T(x,t)可在任意的已知热流度q*处展开成泰勒级数,略去一阶以上微商可得到:
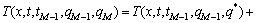
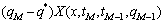 (10)
(10)
式中:
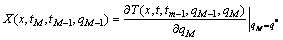 (11)
(11)
采用多个热电偶测量温度,在确定边界热流密度qM时,可用最小二乘法来获得误差为
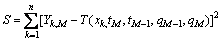 (12)
(12)
由式(12)求导可获得:
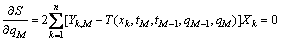 (13)
(13)
而在tM时刻,内点xk处温度场的泰勒级数展开式为
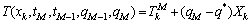 (14)
(14)
由式(13)和(14)可得到
 (15)
(15)
根据牛顿冷却定律,便可获得瞬时的传热系数h
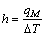 (16)
(16)
式中:qM为零件表面的瞬时热流密度;△T为零件表面的瞬时温差。
4 实验结果与分析
4.1 瞬态温度的变化
板料在加热炉中被加热至950 ℃后转移至实验设备温度降至860 ℃,模具温度为室温20 ℃,在压力为4 MPa时,其界面温度变化如图5所示。从图5可以看出:在板料和模具接触瞬间,温差较大且发生剧烈的热交换,随着热量的传递,温差越来越小,传热的驱动力也有所降低,换热速率减缓,表现为各自温度变化缓慢。值得注意的是:在换热过程进行到4 s左右时,各自的温度曲线出现波动,这是由于在大约390 ℃板料发生相变,释放潜热所致。根据反传热问题的求解方法,可求得各压力下随温度变化的接触瞬态换热系数。

图5 压力为4 MPa时的温度随时间的变化
Fig. 5 Variation of temperature with time at pressure of 4 MPa
4.2 温度的影响
温度对换热系数的影响是多方面的。各压力下换热系数随温度的变化如图6所示。从图6可以看出:换热系数总体随着板料温度的降低而逐渐减小,然而在界面平均温度为280 ℃时,即板料温度为390 ℃左右时,却出现一定的波动,其主要原因是:首先,板料在390 ℃左右时,达到马氏体转变温度点发生了马氏体转变,而马氏体的热导率要高于奥氏体的热导 率[11],整体的换热能力得到提高,且奥氏体转变为马氏体后体积增大,造成板料与模具的接触更加紧密,接触点更多,二者共同影响整体的换热能力。从图6可见:280 ℃时换热系数增大。其次,板料与模具接触后二者的温差越来越小,温差的缩小大大降低了二者换热的驱动力,造成换热速率减缓,换热系数也就随着温差的减小而逐渐减小。再次,温度对热导率的影响也是不容忽视的,在纯金属中,导热机理为自由电子的传导,随着合金程度的增加,导热效率为自由电子和声子导热的总和[12],当温度较低时,合金的热导率随温度的升高而减小,但当温度较高,其对溶质原子热阻率的影响起主导作用时,合金的热导率随温度的升高而增加[10],这与文献[9]中关于高强钢BR1500HS热导率的变化趋势是一致的。而文献[10]中模具钢5CrMnMo的热导率在实验温度范围内随温度的升高而下降,而在界面平均温度为150 ℃时整体的热导率变化比较大,故温度通过对热导率的影响进而影响换热系数的变化。
温度除了通过影响材料的相变和热导率来影响换热系数外,还可以通过改变材料的表面硬度和弹性模量来影响材料表面的变形从而对换热系数产生影响。温度越高,材料表面硬度越小,弹性模量越小,相同压力下,高温时材料表面变形较大,模具和板料的真实接触面积越大,热量可以通过更多的接触点进行热量传递,反之,低温时硬度上升,弹性模量下降造成接触面积减小。且随着温度的下降,材料表面氧化作用越来越显著,而表面氧化物不仅硬度较大,其热导率相对于金属基体要小得多[2],所以换热系数通过以上几方面的综合影响而发生改变,随着温度的降低,换热系数基本呈现减小的趋势。

图6 温度对换热系数的影响
Fig. 6 Effect of temperature on heat transfer coefficient
4.3 压力的影响
换热系数在各界面温度下随着压力的变化曲线如图7所示。从图7可以看出:换热系数与压力的关系也呈正相关关系,即随着压力的增大,换热系数增大,这是由于随着压力的升高,模具和板料的接触更加紧密,造成实际接触面积增大,热量可以通过更多的实际接触点进行传递,表现为换热系数的增大。从图7还可以看出:在同一界面温度下,随着压力的增大,曲线的斜率越来越小,即高压区换热系数对压力的敏感性比低压区换热系数对压力的敏感性差,其原因在于:随着压力的增大,表面微凸体的变形逐渐由弹性变形向塑性变形转化,变形逐渐趋于完全,可变形的微凸体越来越少,实际接触面积的增大趋势越来越平稳,表现为换热系数在同一温度下随着压力的增大,敏感性降低。且随着界面温度的升高,曲线在高压区与低压区的差值增大,曲线整体的平均斜率随着温度的升高逐渐增大,即换热系数随着温度的升高对压力的敏感性增加,这是由于高温时材料硬度较低,增加同样的压力,高温时材料表面的微凸体变形相对低温区变形更大,实际接触面积增加更快,在图7中表现为温度越高,曲线随压力的变化越快,所以温度越高,换热系数对压力的敏感性越强。
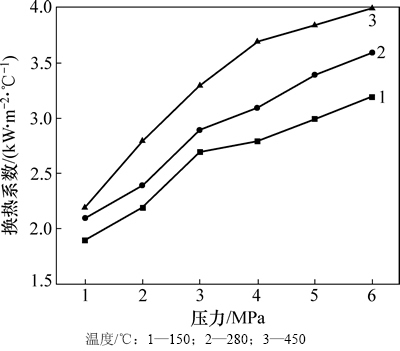
图7 压力对换热系数的影响
Fig. 7 Effect of pressure on heat transfer coefficient
4.4 保温时间的影响
压力为2 MPa以及界面平均温度为450 ℃时,换热系数随着保温时间的变化曲线如图8所示。从图8可以看出:随着保温时间的增加,换热系数逐渐减小。其原因在于,保温时间越长,板料氧化越严重,而氧化物的热导率比金属基体的小得多[2],所以换热系数随着保温时间的增加而减小。而5 min以后,随着保温时间的增加,换热系数变化趋势减小,其可能是由于在5 min前板料氧化较严重,氧化速率较快,而5 min后,氧化物形成致密的氧化物薄膜阻止氧气的进一步氧化,氧化速率较慢。所以在实际生产中奥氏体化后应尽量缩短保温时间,可避免板料的进一步氧化,从而达到较好的淬火效果。

图8 保温时间对换热系数的影响
Fig. 8 Effect of holding time on heat transfer coefficient
4.5 换热系数与温度和压力的拟合
文献[13]中对于换热系数在一定压力下与温度的关系为
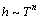 (17)
(17)
文献[14]中对于换热系数在一定温度下与压力p的关系为
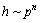 (18)
(18)
对于本实验,按照幂函数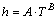 ,
,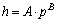 的形式拟合,其中:A,B为拟合参数,结果如图9所示。换热系数与温度拟合时,指数范围为0.172~0.224,拟合优度范围为0.868~0.942;换热系数与压力拟合时,指数范围为0.298~0.335,且指数随着温度的增大而增大,拟合优度范围为0.976~0.984。从拟合结果的指数范围也可以看出:温度对换热系数的影响不及压力对换热系数的影响,即压力对换热系数的影响最大,且温度越高,换热系数对压力的敏感性越强。文献[15]给出了换热系数基于材料表面变形时的最小二乘拟合,其结果为
的形式拟合,其中:A,B为拟合参数,结果如图9所示。换热系数与温度拟合时,指数范围为0.172~0.224,拟合优度范围为0.868~0.942;换热系数与压力拟合时,指数范围为0.298~0.335,且指数随着温度的增大而增大,拟合优度范围为0.976~0.984。从拟合结果的指数范围也可以看出:温度对换热系数的影响不及压力对换热系数的影响,即压力对换热系数的影响最大,且温度越高,换热系数对压力的敏感性越强。文献[15]给出了换热系数基于材料表面变形时的最小二乘拟合,其结果为
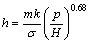 (19)
(19)
其中:m为材料表面微凸体的平均斜度;σ为材料表面的粗糙度;k为材料的热导率;H为材料表面的硬度。对于给定的材料,m和σ都是一定的,而k和H都是温度的函数。由前面的拟合结果可知:换热系数与温度和压力近似呈幂函数的关系,所以对于保温5 min换热系数与温度和压力的拟合方程式可设置为
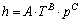 (20)
(20)
式中:C为拟合参数。
通过origin拟合结果如图10所示,其曲面方程为
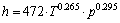 (21)
(21)
其中,拟合优度为0.966 67,拟合结果较好。从拟合结果也可以看出:对于给定的材料,在保温时间等条件确定的情况下,换热系数只是温度和压力的函数,热导率、硬度、表面接触状态都随温度和压力的改变而变化。
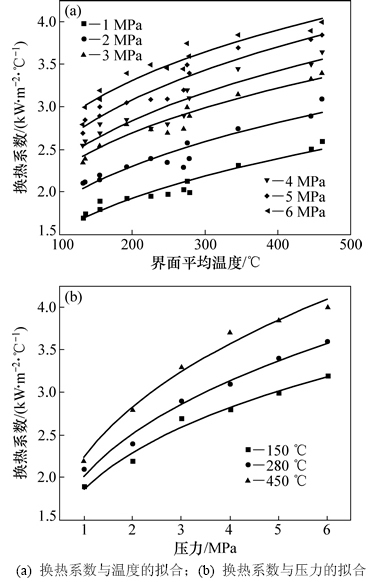
图9 换热系数分别与温度和压力的拟合结果
Fig. 9 Fitting results of heat transfer coefficient with temperature or pressure
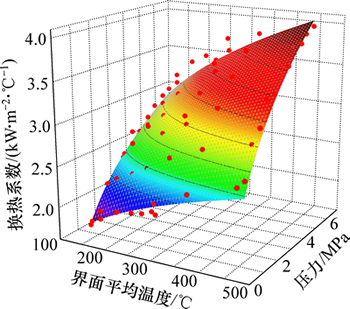
图10 换热系数与温度和压力的拟合结果
Fig. 10 Fitting results of heat transfer coefficient and temperature and pressure
5 结论
1) 将模具和板料之间的传热简化为一维传热并进行了模拟验证,利用改进的瞬态反传热算法求解了换热系数的变化。
2) 板料冷却过程中,随着温度的下降,材料的热导率发生改变,表面硬度和弹性模量增加,造成换热系数随着温度的降低而逐渐下降且在390 ℃时由于发生相变释放潜热,导致换热系数出现一定的波动。
3) 随着压力的增加,实际接触面积增加,换热系数增大,且同一界面温度下换热系数增加趋势逐渐减小,界面平均温度越高,换热系数对压力的敏感性越强。
4) 随着保温时间的增加,换热系数逐渐减小,但保温时间超过5 min后换热系数的减小趋势减慢。
5) 将换热系数对温度和压力进行了整体拟合,对于给定的高强钢和模具,换热系数只是温度和压力的函数,与温度或压力近似呈幂函数的关系,压力对换热系数的影响要大于温度的影响,量化后的表达式对于热冲压过程的准确数值模拟具有十分重要的意义。
参考文献:
[1] Tondini F, Bosetti P, Bruschi S. Heat transfer in hot stamping of high-strength steel sheets[J]. Journal of Engineering Manufacture, 2011, 225(10): 1813-1825.
[2] HU Ping, YING Liang, LI Ye, et al. Effect of oxide scale on temperature-dependent interfacial heat transfer in hot stamping process[J]. Journal of materials Processing Technology, 2013, 213(9): 1475-1483.
[3] Bosetti P, Bruschi S, Stoehr T, et al. Interlaboratory comparison for heat transfer coefficient identification in hot stamping of high strength steels[J]. International Journal of Material Forming, 2010, 3(1): 817-820.
[4] 朱智, 张立文, 顾森东, 等. Hastelloy C-276合金与硅钢间的瞬态接触换热实验研究[J]. 中南大学学报(自然科学版), 2012, 43(3): 877-882.
ZHU Zhi, ZHANG Liwen, GU Sendong, et al. Experimental investigation of transient contact heat transfer between Hastelloy C-276 and silicon steel[J]. Journal of Central South University (Science and Technology), 2012, 43(3): 877-882.
[5] 邢磊, 张立文, 张兴致, 等. TP2铜与3Cr2W8V模具钢的瞬态接触换热系数[J]. 中国有色金属学报, 2010, 20(4): 662-666.
XING Lei, ZHANG Liwen, ZHANG Xingzhi, et al. Transient contact heat transfer coefficient between TP2 copper and 3Cr2W8V die steel[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(4): 662-666.
[6] Gopal V, Whiting M J, Chew J W, et al. Thermal contact conductance and its dependence on load cycling[J]. International Journal of Heat and Mass Transfer, 2013, 66(11): 444-450.
[7] Bai Q, Lin J, Zhan L, et al. An efficient closed-form method for determining interfacial heat transfer coefficient in metal forming[J]. International Journal of Machine Tools and Manufacture, 2012, 56: 102-110.
[8] 顾剑锋, 潘健生, 胡明娟, 等. 淬火冷却过程中表面综合换热系数的反传热分析[J]. 上海交通大学学报, 1998, 32(2): 19-23.
GU Jianfeng, PAN Jiansheng, HU Mingjuan, et al. Inverse heat conduction analysis of synthetical surface heat transfer coefficient during quenching process[J]. The Journal of Shanghai Jiao Tong University, 1998, 32(2): 19-23.
[9] 刘祥意. 汽车前地板热冲压成形模具设计及冷却效果仿真分析[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2012: 34-38.
LIU Xiangyi. Design of the hot stamping mold of automotive front floor and analysis in the simulated quenching effect[D]. Harbin: Harbin Institute of Technology. College of Mechanical and Electrical Engineering, 2012: 34-38.
[10] 苏铁健, 王富耻, 李树奎, 等. 钢的热导率与化学成分和温度的关系[J]. 兵器材料科学与工程, 2004, 27(5): 14-17.
SU Tiejian, WANG Fuchi, LI Shukui, et al. Regression relationships established for thermal conductivity of steel as function of chemical composition at various temperatures[J]. Ordnance Material Science and Engineering, 2004, 27(5): 14-17.
[11] 廖铮玮, 盈亮, 胡平, 等. 高强度钢板热成形界面换热系数估算[J]. 材料热处理学报, 2013, 34(增刊): 167-171.
LIAO Zhengwei, YING Liang, HU Ping, et al. Estimation of interface heat transfer coefficient of ultra high strength steels in hot forming[J]. Transactions of Materials and Heat Treatment, 2013, 34(Suppl): 167-171.
[12] XU Ruiping, XU Lie. An experimental investigation of thermal contact conductance of stainless steel at low temperatures[J]. Cryogenics, 2005, 45(10/11): 694-704.
[13] BI Dongmei, CHEN Huanxin, TIAN Ye. Influences of temperature and contact pressure on thermal contact resistance at interfaces at cryogenic temperatures[J]. Cryogenics, 2012, 52(7/8/9): 403-409.
[14] DING Chang, WANG Rongshun. Thermal contact conductance of stainless steel-GFRP interface under vacuum environment[J]. Experimental Thermal and Fluid Science, 2012, 42(5): 1-5.
[15] Kumar S S, Ramamurthi K. Thermal contact conductance of pressed contacts at low temperatures[J]. Cryogenics, 2004, 44(10): 727-734.
(编辑 赵俊)
收稿日期:2014-12-21;修回日期:2015-03-12
基金项目(Foundation item):中央高校基本科研业务费专项资金资助项目(CDJZR13130082)(Project (CDJZR13130082) supported by the Fundamental Research Funds for the Central Universities)
通信作者:夏玉峰,副教授,从事塑性成形及模具设计研究;E-mail:xyfeng@cqu.edu.cn