基于谱分解技术的分频AVO反演
周竹生,杨鑫
(中南大学 地球科学与信息物理学院,湖南 长沙,410083)
摘要:基于Chapman岩石物理模型,对第三类AVO类型进行频率依赖性分析。并将频谱分解技术与AVO技术结合起来,将反射系数替代为不同频率的振幅谱,将振幅谱视为频率的函数,对Smith & Gidlow近似式进行扩展,给出一种新的描述地震波频散程度的属性的计算公式与方法。并用模型和实际地震资料频散属性的计算。研究结果表明:频散模型和弹性模型的频散属性有明显差异,频散属性可以作为一种含气储层的指示剂。
关键词:分频AVO;Chapman岩石物理模型;频谱分解;气层检测
中图分类号:P631 文献标志码:A 文章编号:1672-7207(2014)04-1197-08
Frequency-dependent AVO inversion using spectral decomposition technique
ZHOU Zhusheng, YANG Xin
(School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)
Abstract: Frequency-dependent characteristics of a class 3 AVO model were performed using Chapman rock physical model. Treating the spectral amplitude as reflective coefficients, a new seismic attribute for the description of seismic dispersion was presented by extending Smith & Gidlow’s formula in frequency domain. Then the method was used for synthetic model and real seismic data processing. The results show that dispersion properties obtained by frequency-dependent inversion can be used as the indicator for hydrocarbon detection, because it is very different in elasticity situation and dispersion situation.
Key words: frequency-dependent AVO; Chapman rock physical model; spectral decomposition; hydrocarbon detection
地震勘探一直以来都是油气勘探的主要方法。AVO(amplitude versus offset)技术是一项利用地震振幅信息推断地层岩性和含油气情况的技术,经过不断的发展和实践,该技术已在油气勘探领域中处于不可替代的地位[1]。它利用Zoeppritz方程或其近似方程对叠前数据进行反演、估计AVO属性参数,建立油气检测的标志,在国内外已有许多成功的实例[2-4]。AVO反演方法是能更为合理地提取隐藏在地震信息中的岩性参数,预测岩性和烃类的重要途径。目前,AVO技术在以下几个方面已经获得较为成功的应用[5]:(1) 用AVO零炮检距剖面做叠后岩性研究;(2) 识别亮点、平点和暗点;(3) 在薄互层情况下,用含油气砂岩的AVO特征来预测油气;(4) 预测碳酸盐岩储层的孔隙度和流体性质等。然而,常规的AVO技术忽略了频率因素。事实上,地震波波速与频率之间的关系十分密切,尤其当地震波经过储层时会发生异常高的速度频散和衰减。含流体储层频变特征的基础主要是岩石物理理论。包括Gassmann理论[6]、Biot理论[7]、喷射流动理论[8]、BISQ理论[6-9]。Chapman等[10]基于喷射流动机制,建立动态弹性孔隙模型来描述裂隙岩石中孔隙与裂隙之间,因地震波引起的流体交换,并在模型中考虑了地震波传播的频散和衰减特性。研究结果表明多孔介质含流体后的地震波响应特征具有频变特性,地震波的散射或吸收会引起地震响应的频散与衰减。本文作者以Zoeppritz方程为基础,从地震波反射系数与频率关系出发,利用现代频谱分解作为频率属性提取的工具,研究频散AVO属性提取方法与分析技术。
1 方法原理
1.1 Chapman多尺度裂隙介质理论
Chapman的多尺度裂隙介质理论认为,模型的有效弹性刚度张量可以表示为[10-11]
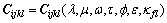 (1)
(1)
式中:λ为拉梅常数;μ为剪切模量;ω为角频率;τ为时间尺度;f为孔隙度;ε为裂隙密度;κfl为填充空隙的流体体积模量。式(1)又可以分解成骨架各向同性介质的张量矩阵 和裂隙与孔隙引起的扰动量矩阵
和裂隙与孔隙引起的扰动量矩阵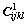 :
:
 (2)
(2)
假设在特定频率ω0下填充孔隙的流体体积模量为 ,其他需要的相关参数有时间尺度τ0,裂隙密度ε0,岩石纵、横波速度可表示为[11]
,其他需要的相关参数有时间尺度τ0,裂隙密度ε0,岩石纵、横波速度可表示为[11]

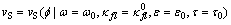 (3)
(3)
由此可得:

 (4)
(4)
引入参数 ,使其满足:
,使其满足:
 (5)
(5)
因此,对于任意频率、流体体积模量及时间尺度,弹性张量可表示为[11]
 (6)
(6)
这样即可求取频率依赖的纵横波速度和品质因子。Chapman多尺度裂隙介质与实际储层的介质特征非常近似。基于该理论,可以推导出地震波的AVO响应与频率之间的关系,进而获得频散属性。
1.2 分频AVO理论
本文基于Smith和Gidlow的Zoeppritz方程近似式[12],反射系数可以写为
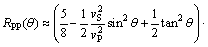
 (7)
(7)
假设由于频散性质的存在,界面每一边的反射系数随频率变化。特别地,认为P波S波阻抗随频率变化,得到具有频率依赖性的AVO近似:
 (8)
(8)
对式(8)在频率fc处进行Taylor级数展开:
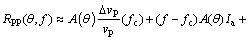
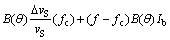 (9)
(9)
式中:
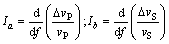 (10)
(10)
式(10)所示为纵横波速度变化率随频率的变化(频散属性)。频散属性的大小直接体现了岩石中的含气情况,可作为一种新的烃类指示剂。
1.3 频谱分解技术
对于一道地震数据x(t),利用频谱分解技术可以获得某一频率fi下的单频数据S(t,fi),而S(t,fi)包括了反射系数ref、地震子波wave、随机噪声noise的影响:
 (11)
(11)
因此,必须消除地震子波、随机噪声的影响。随机噪声可以在预处理中去除,因而地震子波的影响占主要地位,需要通过对地震数据的频谱乘加权函数ω进行谱能量均衡:
 (12)
(12)
这样均衡单频数据SB(t,fi)只包含了反射系数的能量谱,根据频散AVO反演理论,对其加以利用,即可求取地震资料中的频散属性。
2 模型分析
建立弹性模型和频散模型,首先研究两者的AVO响应与频率的关系,然后进行分频AVO反演和频散属性分析。模型参数如表1所示,第1层为泥岩,第2层为砂岩,气填充岩石中的空隙后,使得模型下层具有了频散属性。
表1 模型参数
Table 1 Model parameters

图1所示为2种模型不同频率的反射系数曲线。从图1可以看出:弹性模型的反射系数不会随频率变化,而频散模型具有频率依赖性,反射系数随频率的降低而减小。但由于模型具有第三类AVO反射特征,所有反射系数均为负,因此,低频极限的反射系数绝对值大于高频极限反射系数的绝对值。在气饱和状态下,能量向低频方向移动。形成储层部位的“低频阴影”[13-18]。
采取主频为45 Hz的雷克子波作为震源,模拟弹性与频散模型的地震记录。如图2所示。由图2可以看出:垂直入射振幅为负,振幅随角度变化而逐渐减小。
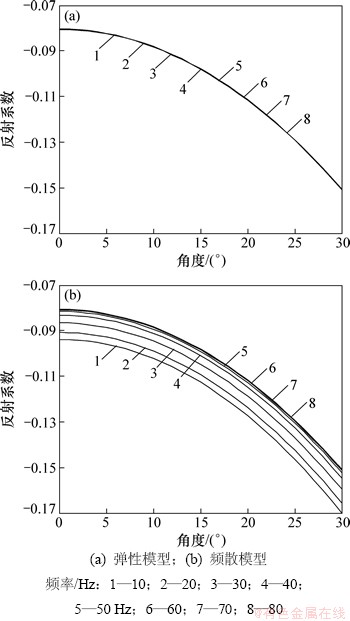
图1 界面处各频率的反射系数
Fig. 1 Reflective coefficients at different frequencies
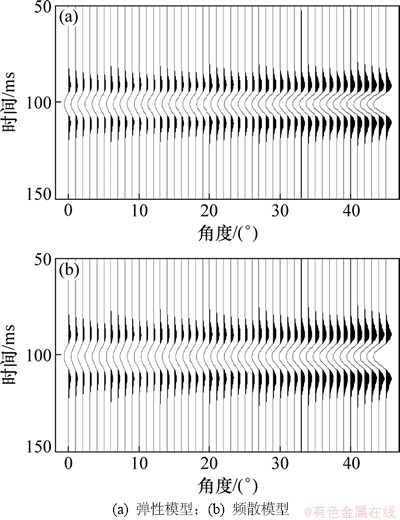
图2 弹性和频散模型的AVO地震模拟记录
Fig. 2 Synthetic record for elastic model and dispersion model
对合成的地震记录进行频谱分解。取每一道谱分解后频率为10,20,30,40,50,60,70和80 Hz 在界面(100 ms处)时对应的谱振幅,如图3所示。
弹性介质能量在地震子波主频(40和50 Hz)附近最强,频散介质模型能量向低频方向有所移动。主频附近AVO反射特征明显,而低频能量较弱,不能明显反映AVO特征。尽管两者有细微不同,弹性介质和频散介质的能量大体分布还是一致的。这是由于单频剖面的谱振幅受地震子波的影响。要想进一步探讨AVO反射振幅特征随频率的变化,就要对各个单频数据进行谱均衡来消除这种影响。对图3各个频率的曲线进行谱均衡得到如图4所示的结果。

图3 不同频率对应的谱振幅
Fig. 3 Spectral amplitude s at different frequencies
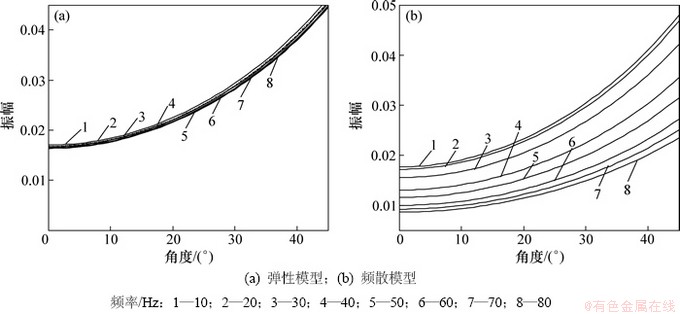
图4 不同频率对应的振幅谱(均衡后)
Fig. 4 Spectral amplitudes at different frequencies (balanced)
由图4可以看出:经过谱均衡后,弹性介质中反射振幅谱不再随频率变化而变化,各频率曲线与主频曲线重合(选取地震子波主频作为参考频率);而频散介质中反射振幅谱呈现了明显的频率依赖性,能量随频率由高到低逐渐减弱。这与图1所示结果相吻合。
以地震波主频45 Hz为参考频率,在10~80 Hz处展开,反演得到的纵波频散属性如图5所示。从图5可以看出:频散属性的差异来可以区分弹性介质和频散介质,含气储层中,孔隙中的烃类会导致岩石的非均质性增强,地震波传播过程中,流体和岩石骨架之间的相对运动更为剧烈,频散程度一般较大,因此,可以用其作为一种烃类指示剂来检测岩石的含气性。
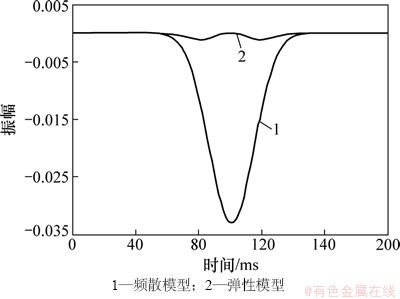
图5 频散模型与弹性模型的纵波频散属性对比
Fig. 5 Comparison of dispersion property between elastic and dispersion model
3 实际地震资料试算
图6所示为某区的实际地震CDP叠加剖面,采样率2 ms,地震资料主频在40 Hz左右,目的层为含气砂体储层1和储层2(椭圆所示区域)。
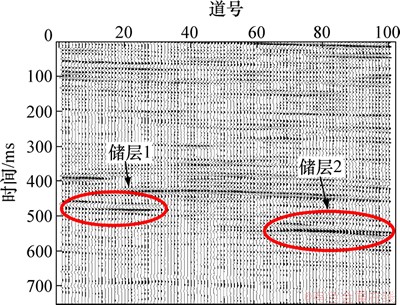
图6 实际地震CDP叠加剖面
Fig. 6 A real-data CDP stacked section
对地震剖面进行频谱分解处理,获得地震记录的45,30,15和10 Hz的分频剖面,如图7所示。从图7可以看到:储层1和2在45 Hz的分频剖面上没有明显的体现;在30 Hz的分频剖面上,储层1和2处的能量有了加强;在15 Hz的分频剖面上,储层1和2处的能量有了明显加强,储层1和2的埋深及其形态都体现得非常清楚,且剖面上的干扰因素减少到最少;当分频频率进一步降低到10 Hz时,除了储层区域的能量团,在700 ms左右处也出现了低频异常。由于此异常在叠加剖面上没有明显体现,因此,不能推断它是储层所致。
虽然15 Hz分频剖面可以探测含气砂岩储层所处的位置、形态等方面的特征。但是,为了进一步对地震资料进行研究,充分利用叠前数据的高低频信息,对叠前数据进行分频AVO反演,以第20道(储层1位置)为例,叠前地震资料主频在40和50 Hz左右,带宽为0~80 Hz。叠后地震道的主频在40 Hz左右(50 Hz的高频能量有所减小),带宽为0~80 Hz。对第20道叠前道集进行频谱分解。频率分别为10,25,35,45,55和70 Hz,如图8所示。由图8可以看出:分频剖面的频谱能量在此地震道主频40 Hz附近最强,且随频率与主频的偏离而减小。

图7 实际地震资料的单频剖面
Fig. 7 Common frequency section of real data
对数据进行谱均衡,结果如图9所示。从图9可以看出:400~500 ms处的同相轴能量随频率的升高而减弱,符合第三类AVO低频能量增强的特征。这种变化特征可能与流体填充导致的频散特性有关。进一步进行频散属性反演以定量地确定这种变化。
以主频40 Hz为参考频率,在10~100 Hz频率处展开进行频散属性的分频AVO反演,结果如图10所示。从图10可以看出:在叠前道集上470~480 ms的同相轴振幅随角度增加而增加,体现出第三类AVO反射特征;频散属性在此处有较大的负值,体现了第三类AVO频散特征;而430~440 ms的同相轴却没有明显的反映,很可能是岩性差异所致。在图7中10 Hz单频剖面上600~700 ms处出现的低频阴影在频散曲线上也未有明显反映。
对每一道进行分频AVO反演,可得如图11所示频散属性剖面图。从图11可见:背景值基本在0附近,在图6中标出的储层位置,有较大的负值频散,可以推测该异常由含气储层引起。由于频散属性值表征频散程度,一些上下波阻抗差异引起的强反射也被削弱,并且能够排除一些虚假的频率异常,突出了具有高频散属性的位置。而含气储层一般具有这种性质,因此,频散属性可以作为一种新的烃类指示剂。
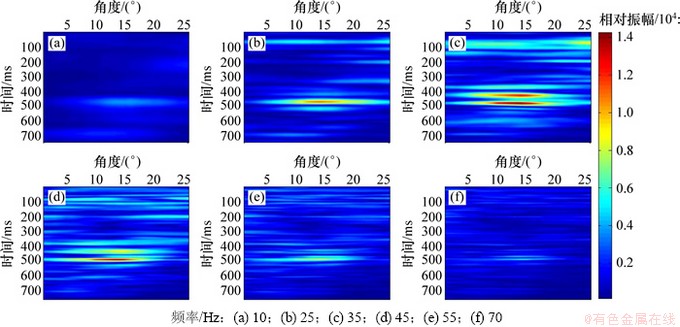
图8 第20道叠前道集的单频剖面
Fig. 8 Common frequency section of the 20th pre-stacked gathers

图9 第20道叠前道集的单频剖面(谱均衡后)
Fig. 9 Common frequency section of the 20th pre-stacked gathers (balanced)

图10 第20道叠前道集及反演得到的纵波频散属性
Fig. 10 20th pre-stacked gathers and the P-wave dispersion property

图11 纵波频散属性剖面
Fig. 11 P-wave dispersion property section
4 结论
(1) 地震波的反射系数与频率密切相关,据此可以推导出地震波的AVO响应与频率之间的关系,进而获得频变AVO属性。
(2) 以频谱分析技术为手段,对叠前地震资料进行时-频谱分析,获得了能够区分弹性介质与频散介质的频散属性,充分利用了叠前资料丰富的振幅和频率信息,有效抑制了叠后地震资料中的部分“频率异常”干扰,基本实现了含气储层的直接检测。
参考文献:
[1] 殷八斤, 曾灏, 杨在岩. AVO技术的理论与实践[M]. 北京:石油工业出版社, 1995: 46-55.
YIN Bajin, ZEN Hao, YANG Zaiyan. Theory and practice of AVO technique[M]. Beijing: Petroleum Industry Press, 1995: 46-55.
[2] 尚永生, 杨长春, 王真理, 等. 塔里木盆地卡4区块AVO研究[J]. 地球物理学进展, 2007, 22(5): 1408-1415.
SHANG Yongsheng, YANG Changchun, WANG Zhenli, et al. AVO research in Ka-4 region Tarim basin[J]. Progress in Geophysics, 2007, 22(5): 1408-1415.
[3] Fatti J L, Smith G C, Vail P J, et al. Detection of gas in sandstone reservoirs using AVO analysis[J]. Geophysics, 1994, 59(9): 1362-1376.
[4] 李景叶, 陈小宏, 郝振江, 等. 多波时移地震AVO反演研究[J]. 地球物理学报, 2005, 48(4): 902-908.
LI Jingye, CHEN Xiaohong, HAO Zhenjiang, et al. A study on multiple time-lapse seismic AVO inversion[J]. Chinese Journal of Geophysics, 2005, 48(4): 902-908.
[5] 宋建国, 王艳香, 乔玉雷, 等. AVO技术进展[J]. 地球物理学进展, 2008, 23(2): 508-514.
SONG Jianguo, WANG Yanxiang, QIAO Yulei, et al. Advances in AVO technique[J]. Progress in Geophysics, 2008, 23(2): 508-514.
[6] Gassmann F. Elastic waves through a packing of spheres[J]. Geophysics, 1951, 16(4): 673-682.
[7] Biot M A. Theory of propagation of elastic waves in a fluid saturated porous solid. I: Low-frequency range[J]. Journal of the Acoustical Society of America, 1956, 28(2): 168-178.
[8] Mavko G, Jizb A D. Estimating grain-scale fluid effects on velocity dispersion in rocks[J]. Geophysics, 1991, 56(12): 1940-1949.
[9] Dvokin J, Mavko G, Nur A. Squirt flow in fully saturated rocks[J]. Geophysics, 1995, 60(1): 97-107.
[10] Chapman M, Zatsepin S V, Crampin S. Derivation of a micro structural poroelastic model[J]. Geophysical Journal International, 2002, 151(2): 427-451.
[11] Chapman M. Frequency-dependent anisotropy due to meso-scale fractures in the presence of equant porosity[J]. Geophysical Prospecting, 2003, 51(1): 369-379.
[12] Smith G, Gidlow P. Weighted stacking for rock property estimation and detection of gas[J]. Geophysical Prospecting, 1987, 35(9): 993-1014.
[13] Ebrom D. The low-frequency gas shadow on seismic sections[J]. The Leading Edge, 2004, 23(8): 772.
[14] Partyka G A, Gridley J M, Lopez J. Interpretational applications of spectral Decomposition in reservoir characterization[J]. The Leading Edge, 1999, 18(3): 353-360.
[15] Castagna J P, Sun S J, Siegfried R W. Instantaneous spectral analysis: Detection of low-frequency shadows associated with hydrocarbons[J]. The Leading Edge, 2003, 22(3): 120-127.
[16] 刁瑞, 李振春, 韩文功, 等. 基于广义S变换的吸收衰减分析技术在油气识别中的应用[J]. 石油物探, 2011, 50(3): 260-265.
DIAO Rui, LI Zhenchun, HAN Wengong, et al. Application of absorption and attenuation analysis technique based on generalized S transform for hydro carbon identification[J]. Geophysical Prospecting for Petroleum, 2011, 50(3): 260-265.
[17] 王栋, 贺振华, 黄德济. 时频谱分析在油气储层预测中的应用[J]. 天然气工业, 2009, 29(4): 36-38.
WANG Dong, HE Zhenhua, HUANG Deji. Application of time frequency spectrum to oil and gas reservoir prediction[J]. Natural Gas Industry, 2009, 29(4): 36-38.
[18] 刘兰峰, 曹思远, 李绪宣, 等. 未固结含气砂岩储层低频地震响应特征研究[J]. 石油地球物理勘探, 2010, 45(6): 873-878.
LIU Lanfeng, CAO Siyuan, LI Xuxuan, et al. Studies on the characteristics of frequency seismic response from unconsolidated gas-bearing sand reservoir[J]. Oil Geophysical Prospecting, 2010, 45(6): 873-878.
(编辑 杨幼平)
收稿日期:2013-06-25;修回日期:2013-09-10
基金项目:国家自然科学基金资助项目(41074085,40804027);湖南省自然基金重点资助项目(09JJ3084)
通信作者:周竹生(1965-),男,湖南祁阳人,博士后,教授,从事资源勘查、工程物探、地质灾害调查、信号处理、应用软件研制及数据库开发等研究;电话:13707316924;E-mail:geophys@126.com