基于闭合模式的高维基因表达谱多类分类
李 宏,李 翔,吴 敏,陈松乔,易丽君
(中南大学 信息科学与工程学院,湖南 长沙,410083)
摘 要:针对多类高维基因表达谱的特点,提出一种基于闭合模式的多类分类算法CBCP,即根据垂直格式的数据集采用路径枚举的方法挖掘闭合模式,极大地减少了冗余模式的产生。然后,对所有闭合模式进行排序,通过覆盖训练集建立分类器。针对分类器无法识别的样本提出权重算法进行判断,克服了使用Default类预测不精确的问题。研究结果表明,CBCP与经典分类算法如CBA和C4.5相比具有更高的预测准确率,并且在基因数大幅增加而样本数不变的情况下仍具有较强的稳定性,证明CBCP的可扩展性强,适用于高维数据集的多类分类预测。
关键词:关联规则;闭合模式;多类别;权重算法
中图分类号:TP274 文献标识码:A 文章编号:1672-7207(2008)05-1035-07
Multi-class classification of high-dimension gene expression profile based on closed patterns
LI Hong, LI Xiang, WU Min, CHEN Song-qiao, YI Li-jun
(School of Information Science and Engineering, Central South University, Changsha 410083, China)
Abstract: According to the characteristics of multi-class high-dimension gene expression profile, a new multi-class classification algorithm(CBCP) based on closed pattern was designed. Firstly an approach called path enumeration was proposed to mine closed patterns based on the vertical formatted data-table, which can reduce most redundant patterns. Then closed patterns were sorted and used to cover train dataset for building the classifier. The unrecognized samples were classified by weight algorithm, which can overcome the inaccuracy caused by using Default Class. The results show that the algorithm is proved to be more accurate than classical classification algorithms such as CBA and C4.5. CBCP keeps high accuracy when the number of genes increases substantially with the increase of number of samples fixed, which proves it is suitable for multi-class classification of high dimension datasets, and it is easy to extend.
Key words: association rules; closed pattern; multi-class; weight algorithm
关联规则的发现是数据挖掘领域的一个重要组成部分,是由 Agrawal等提出的在数据库中知识发现(Knowledge discovery in databases,KDD)的重要研究课题,已广泛应用于销售、保险、银行及医学等领 域[1-3]。最近,Bing等[4-8]对关联规则在分类问题中的应用进行了研究和探讨,提出的经典算法有CBA等。这些算法的基本思想是利用现有关联规则挖掘算法产生所有频繁项目集[5],并使用这些频繁项目集构造分类器[4, 6],它们同时考虑所有属性,在低维数据集上,与同样基于决策树的分类算法相比,其分类效果更好。但是,针对多类高维基因表达谱的分类问题,经典的关联规则分类算法仍然存在一些不足:
a. 算法的研究多集中在二类的研究[9-11]。多类别数据关联规则的提取和分类还有待进一步研究和 发展。
b. 算法挖掘的是频繁项集,当最小支持度设置较低时,频繁项集的数量往往非常庞大,因此,会产生大量的冗余关联规则。
c. 高维数据集往往具有样本数和项数不均衡的特点,现有的经典分类算法处理该类数据集时容易产生预测准确率不稳定的情况。
d. 算法将测试集中无法识别的样本直接归为某一个默认类别(Default class),分类结果不够精确。
由于频繁闭合模式惟一决定了所有频繁项集的准确支持度,并且规则数比频繁项集小几个数量级[4],在此,本文作者提出一种基于闭合模式的多类别分类算法CBCP(Classification based on closed patterns),对经典算法的几个不足之处进行改进。首先将n类数据集按类别分成n个子集,针对各子集挖掘频繁闭合模式,然后,对所有的闭合模式进行整合排序,覆盖训练集,建立分类器。闭合模式的挖掘采用基于行枚举思想的路径枚举方法,通过对行集建立行FP-tree[12]挖掘闭合模式,提高了算法效率。构造权重函数,对分类器无法识别的样本用权重系数进行类别判断,比经典算法采用统一默认类别的方式具有更高的可靠性。CBCP算法是一种新的多类别数据的分类方法,该算法基于闭合模式理论以及行枚举、FP-tree技术的特点和优势,提高了分类算法的效率,具有较强的可扩展性。
1 问题描述及相关定义
基于闭合模式的多类别分类是针对多类别数据挖掘闭合模式建立分类器,实现对未知样本分类的方法,可以分为3步:
a. 挖掘闭合模式;
b. 建立分类器;
c. 对测试集进行预测。
给出相关定义如下:给定数据集D,D中的样本记为Di,I为D中所有项的集合,C为样本类别,Y为分类关联规则,A为项的集合(项集),G为规则组,规则组支持集R是行的集合,函数R(A)计算D中包含A的行集,S为Y的支持数,sup为Y的支持度,conf为Y的置信度。
定义1 Y具有如下形式:Y: 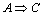 。
。
定义2 Y的支持数S为D中包含A且类别为C的样本个数。
定义3 Y的支持度定义为:
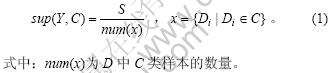
定义4 Y的置信度定义为:

定义5 规则组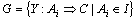 必须满足如下条件:
必须满足如下条件:
a. 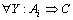 ,那么D中包含Ai的行集
,那么D中包含Ai的行集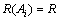 ;
;
b. 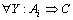 ,若包含Ai的行集
,若包含Ai的行集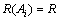 ,则
,则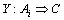 必属于G。
必属于G。
定义6 G的上边界(upper bound)是G中的一条分类关联规则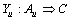 ,Yu满足条件:在G中
,Yu满足条件:在G中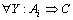 的Ai是Au的子集。
的Ai是Au的子集。
定义7 项集A是闭合模式,则不存在A的超集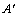 与A的支持数相等[13]。若A是频繁的,则称A为频繁闭合模式。频繁闭合模式惟一决定了所有频繁项的准确支持度,并且尺寸比频繁项集小几个数量级[3]。
与A的支持数相等[13]。若A是频繁的,则称A为频繁闭合模式。频繁闭合模式惟一决定了所有频繁项的准确支持度,并且尺寸比频繁项集小几个数量级[3]。
定理1 给定规则组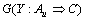 (Au为G的上边界),其规则组支持集为R,则Au惟一,即上边界是惟一的。
(Au为G的上边界),其规则组支持集为R,则Au惟一,即上边界是惟一的。
证明:假设上边界不惟一,则存在另一条上边界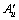 ,
,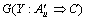 ,A′≠A,且
,A′≠A,且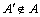 。令
。令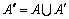 ,由
,由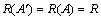 ,可知R(A″)=R,则
,可知R(A″)=R,则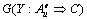 且
且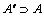 ,因此,Au不是G的上边界。从而上边界必惟一。
,因此,Au不是G的上边界。从而上边界必惟一。
2 CBCP算法设计与实现
2.1 频繁闭合模式的挖掘
采用传统枚举树方法进行闭合模式的挖掘是将行进行枚举组合,计算行组合所包含的公共项集。该方法存在冗余数据多、算法效率低的问题。本文基于行枚举(Row_FP)思想,结合闭合模式和规则组上边 界[13],提出了根据行FP-tree和rt表来构造路径枚举树的路径枚举算法挖掘闭合模式,降低了冗余数据的产生。整个算法的大致流程是:
a. 建立垂直格式的数据集,每个项对应的行按照支持数从小到大排列;
b. 根据垂直数据集建立行FP-tree和rt表;
c. 根据rt表中自底向上的每一行分别建立路径枚举树,并挖掘出闭合模式。
表1所示为水平格式的数据集。
表1 水平格式的数据集
Table 1 Horizontal formatted dataset

表2所示为表1中数据集的垂直结构格式[14]。对其按照FP-tree[1]的构造方法通过1遍扫描建立行FP-tree和rt表。利用行FP-tree可以计算项集以及对应的支持数,行FP-tree中节点到根节点的路径长度即为该节点对应项集的支持数。同时,建立1个rt表,指向在行FP-tree中包含某行且支持数大于最小支持数的所有结点。行FP-tree和rt表的建立结果如图1所示。
表2 垂直格式的数据集
Table 2 Vertical formatted dataset

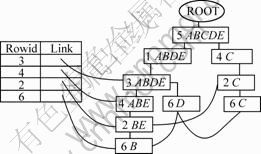
图1 rt表和行FP-tree(最小支持数为3)
Fig.1 rt Table and row FP-tree (MinSup is 3)
定理2 行FP-tree得到的行组合是完备的。
FP-tree采用水平结构对项集进行挖掘,可以没有遗漏地挖掘出所有项集[15],同理,行FP-tree采取垂直结构对行集进行挖掘,得到的行组合也是没有遗漏的。
对于rt表中的行,它的每个路径包含的行组合可分为2类:
a. 由多条路径相同的行组成的行组合;
b. 不被其他路径包含的行组合。
对于第1类组合,它们对应的项集是所有包含此组合的路径对应项集的并集,项集的支持数为相同行的个数;对于第2类行组合,1条路径上所有的此类组合对应的模式均为此路径对应的项集。
通过对rt表中自底向上的每一行的所有路径组合根据路径枚举算法(Path enumeration algorithm, PEA)构造1棵路径枚举树。由于rt表中指向的行FP-Tree节点的支持数均不低于最小支持数的节点数,因此,可以减少PEA算法中冗余模式的产生。路径枚举树中未被剔除节点的项集符合频繁闭合模式规则组上边界的定义,将其并入最终的闭合模式集中。PEA算法描述如下。
a. 定义路径枚举树的节点结构为:
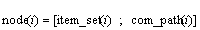
其中: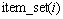 表示节点i的项集,
表示节点i的项集,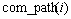 表示
表示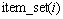 在行FP-tree中的公共的路径。
在行FP-tree中的公共的路径。
b. 将rt表的行号作为路径枚举树的根节点(第0层)。
c. 将rt表该行的路径指针指向的行FP-tree的n个节点的项集和路径作为路径枚举树的第1层节点。
d. 按如下方法构建路径枚举树第w(w初始化为2)层的节点:
n=sum_node(w); // n为w层的节点个数
if (n≥2)
For i=1 to n-1
For j=i+1 to n
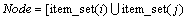 ,
,
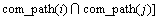 ;
;
将Node作为node(i)的子节点;
剪枝;
End
End
End
e. w=w+1。循环执行步骤d构建路径枚举树。
建树过程中,按下列3条规则进行剪枝:
a. 若路径组合PC1的公共行集合与路径组合PC2的公共行集合相同且PC1包含的路径个数大于PC2包含的路径个数,则PC2包含的公共行集合不符合闭合模式的定义,将PC2删除,PC1和PC2枚举的结果作为PC1的子节点。
b. 对每个路径组合计算公共行的数目,若数目小于最小支持数,则此路径组合被删除。
c. 若路径枚举树中路径组合PC1得到的模式A在前面的挖掘中已经存在,则删除模式A。
图2所示为行6经过剪枝后的路径枚举树。

图2 行6的路径枚举树(最小支持数为3)
Fig.2 Path-enum-tree of row 6 (MinSup is 3)
2.2 分类器的构建
分类器的构建是全算法的关键部分,选择的分类关联规则度直接影响到分类器的分类预测准确性和算法的效率。分类器建立在挖掘出的所有频繁闭合模式的基础上,并且加上了类别信息。
给定数据集D。T和T ′ 分别为水平格式和垂直格式的训练集,样本类别数为n,设置最小置信度MinConf和最小支持数MinSup,CBCP算法的描述如下所示:
a. 将T按类别分解为T1, T2, …, Tn。其中,n为T中的类别数。
b. For c=1 to n
扫描Tc,建立行FP-tree和rt表;
针对rt表建立路径枚举树,挖掘闭合模式集合Uc;
end
c. 令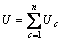 ;
;
d. 对U排序,得到U′。
e. 使用U′对T ′ 进行预测以建立分类器:从U′中取出Y,计算T ′ 中满足Y的样本数i,若i>0,则将Y放入分类器l中,并将Y从U′中剔除,对Y满足的样本从T ′ 中剔除,至U′中所有Y不能再覆盖T ′ 中的任意一条样本,将此时的l作为最终的分类器L。
算法中步骤a将训练集分解成互不耦合的n个部分,步骤b可以通过并行的分布式多机挖掘来实现,以提高算法的运行效率。
算法中步骤d关联规则依据以下原则进行排序:
a. 将U中的Y按照conf降序排列,删除所有低于MinConf的Y;
b. 若2条Y的conf相同,则按照sup降序排列;
c. 若2条规则的conf和sup都相同,则按照支持数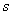 降序排列;
降序排列;
d. 若2条规则的conf,sup和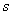 都相同,则按照规则产生的先后顺序排列。
都相同,则按照规则产生的先后顺序排列。
e. 经过以上步骤排序后,若存在2条规则的项集完全相同,则删除靠后的规则。
使用最终分类器L对测试集进行预测,对无法预测的样本采用权重算法(Weight Algorithm, WA)进行判断。WA的描述如下:
a. 初始化权重矩阵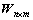 的值为0,其中,n为样本类别数,m为项的数量。用
的值为0,其中,n为样本类别数,m为项的数量。用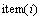 (i=1, …, m)表示第i项的id;
(i=1, …, m)表示第i项的id;
b. 表T ′ 中第i(i=1, …, m) 项中类别为c(c=1, …, n)的样本个数作为该项c类的权重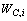 ,得到权重矩阵
,得到权重矩阵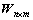 。
。
c. 根据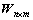 及以下公式分别计算待测样本s各类的权重SWc。
及以下公式分别计算待测样本s各类的权重SWc。

H(i)的定义如下:
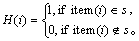 (4)
(4)
d. 选择最大的SWC(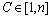 )所在的类别c作为s的类别。
)所在的类别c作为s的类别。
因为训练集中各类样本出现的次数不一定相同,T ′ 中每类别的所有项权重之和并不相等,而是呈比例关系,因此,不能直接通过比较待测样本各类的权重和大小来判断样本类别。权重系数体现了该类样本在T ′ 中所占的比例。
3 实验结果分析及比较
3.1 数据来源及数据预处理
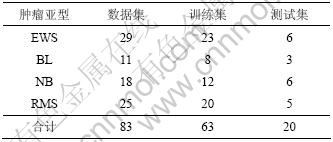
本文实验使用的是小圆蓝细胞(SRBCT)数据 集[15]。该数据集存在4种类型,每个样本由2 308个特征基因组成。数据集的划分如表3所示。
表3 SRBCT样本划分
Table 3 Sample partition of SRBCT
首先,使用基于GB指标(Gini指数与基因的Bhattacharyya距离构建的综合指标)和Euclidean距离对数据集无关基因予以剔除,保留分类信息含量高的信息基因作为数据集D。使用信息基因进行关联规则的挖掘不仅符合基因表达谱数据分析的需要,同时,有利于降低噪声数据对CBCP算法分类准确性的干扰。为证明算法对于高维数据集的适用性,这里仍对未进行剔出操作的数据集进行分类预测。
3.2 实验结果与分析
用VC++ 6.0对CBCP算法进行测试。测试主机为联想万全T200服务器,配置为操作系统为Windows2000 Server,CPU为Intel Xeon 2.4GHz,内存为512MB。
采用CBCP算法对SRBCT数据集经过预处理后保留62个特征基因的数据集,对该数据库进行分类和预测,其结果见表4。可见,当MinSup固定,MinConf低于一定阈值时(如62个基因时MinConf为75%),或者当MinConf固定,MinSup低于一定阈值时(如62个基因时MinSup为60%),分类器的预测准确率达到最高。随着MinSup或MinConf的减小,冗余的闭合模式增多,但最终分类器中的规则数不变,并不影响分类器的预测准确率。当MinConf或MinSup高于阈值时,有效的规则数减少,无法识别的样本数增加,导致分类器的预测准确率降低。虽然权重算法是对分类器的有效补充,被用来预测分类器无法识别的测试集样本,但从分类器的性能来说,支持度和置信度应取能够覆盖最多训练集样本时的参数值。
表4 MinSup固定或者MinConf固定情况下CBCP算法的实验结果(62基因)
Table 4 Results of CBCP with fixed MinConf or fixed MinSup (62 gene)
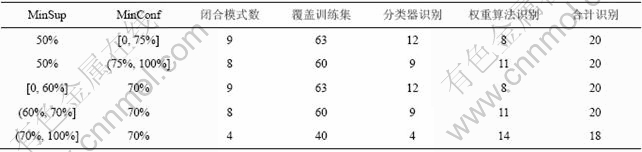
表5所示为采用CBCP算法对7,40,62和82个基因的数据集的最优分类预测结果。可见,当支持度和置信度取值适当时,根据CBCP算法建立的模型可以100%识别训练集和测试集的所有样本,说明CBCP算法适用于维数相对较低的数据集。
表5 MinSup和MinConf最优情况下CBCP算法的实验结果( MinSup=60%,MinConf=50%)
Table 5 Results of CBCP with Best MinSup and MinConf when MinSup=60% and MinConf=50%

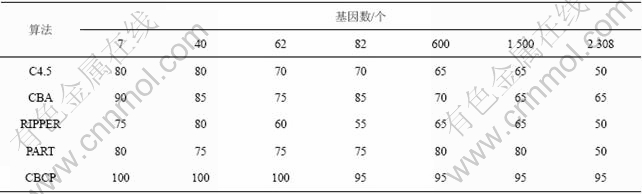
表6和表7所示为针对不同基因数使用CBCP算法和经典分类算法进行预测的结果比较。从表6可见,采用CBCP中对于闭合模式的排序和覆盖的方法构造出来的分类器始终可以完全覆盖训练集。而其他的经典分类算法在基因数增加1个数量级时,对训练集的覆盖准确率有一定程度的降低。从表7可见,对于测试集的预测,由于基因数增加,噪声基因对分类算法的预测精度产生了一定的干扰,CBCP算法预测准确率不再为100%,但是,仍保持了优于其他经典算法的较高准确率,说明在样本数和基因数不均衡的情况下,本算法的预测准确率较稳定,其中权重算法起至关重要的作用。实验结果充分表明,CBCP算法对高维基因表达谱数据集进行预测的适用性和可扩展性高。
表6 不同算法在训练集的预测准确率
Table 6 Accuracy of different algorithms on training datasets %
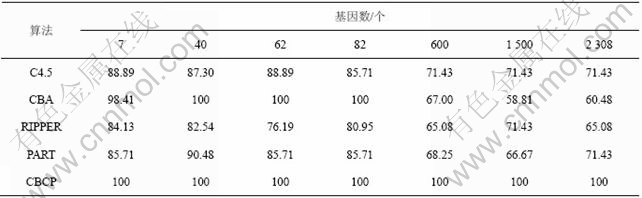
表7 不同算法在测试集的预测准确率
Table 7 Accuracy of different algorithms on test datasets %
4 结 论
a. 提出一种基于闭合模式的多类分类算法CBCP,用于解决高维基因表达谱的多类分类问题。该算法具有如下优点:
1) 使用路径枚举的方法挖掘闭合模式,减少挖掘过程中冗余模式。
2) 用频繁闭合模式作为分类器基础,克服了经典关联分类算法如CBA采用频繁项集作为分类器基础可能导致的规则数量过于庞大的问题。
3) 对分类器无法识别的样本采用权重算法进行判断,精度较高。
b. 通过对小圆蓝细胞(SRBCT)数据集的分类预测,证明了CBCP算法不仅对维数较低的多类数据集具有较高的预测准确率,而且对于基因数大幅度增加而样本数保持不变的高维不均衡数据集,CBCP算法仍具有优于其他经典分类算法的预测准确率,充分说明CBCP对高维基因表达谱多类分类问题的适用性和算法的可扩展性。
参考文献:
[1] HAN Jia-wei, Kamber M. Data mining: Concepts and techniques[M]. Beijing: Higher Education Press, 2001: 10-20.
[2] Doug B, Johannece G, Manuel M. MAFIA: A maximal frequent itemset algorithm for transactional databases[C]//Proceedings of the 17th International Conference on Data Engineering. German: Heidelbergt, 2001: 443-452.
[3] Bastide Y, Pasquier N, Taouil R. Discovering frequent closed itemsets for association rules[C]//Proceedings. of the 7th International Conferenece on Database Theory. Jerusalem: Springer-Verlag, 1999: 398-416.
[4] Bing L, Wayne S, Yiming M. Integrating classification and association rule mining[C]//Proceedings of the 4th International Conference on Knowledge Discovery and Data Mining. New York: AAAI Press, 1998: 80-86.
[5] LI Wen-min, HAN Jia-wei, PEI Jian. CMAR: Accurate and efficient classification based on multiple class association rules[C]// Proceedings of IEEE International Conference on Data Mining. San Jose: CA, 2001: 369-376.
[6] 李 宏, 杜剑峰, 陈松乔. 分布式数据库约束性关联规则挖掘[J]. 中南大学学报: 自然科学版, 2004, 35(6): 998-1003.
LI Hong, DU Jian-feng, CHEN Song-qiao. Mining association rules with item constraints in distributed database[J]. Journal of Central South University: Science and Technology, 2004, 35(6): 998-1003.
[7] 邹晓峰, 陆建江, 宋自林. 基于模糊分类关联规则的分类系统[J]. 计算机研究与发展, 2003, 40(5): 651-656.
ZOU Xiao-feng, LU Jian-jiang, SONG Zi-lin. A classification system based on fuzzy class association rules[J]. Journal of Computer Research and Development, 2003, 40(5): 651-656.
[8] Thabtah H, Cowling P, Yonghong P. MMAC: A new multi-class, multi-label associative classification approach//Proceedings of IEEE International Conference on Data Mining. Brighton, 2004: 217-224.
[9] Lim T, Weiyin L. A comparison of prediction accuracy, complexity and training time of thirty-three old and new classification algorithms[J]. Machine Learning, 2000, 40: 203-228.
[10] Quinlan J. C4.5: Programs for machine learning[M]. San Francisco: Morgan Kaufmann, 1993: 56-89.
[11] YIN Xiao-xin, HAN Jia-wei. CPAR: Classification based on predictive association rule[C]// SDM 2003. San Francisco: CA, 2003.
[12] MAO Run-ying, HAN Jia-wei, PIE Jian. CLOSET: An efficient algorithm for mining frequent closed itemsets[C]//Workshop on Data Mining and Knowledge Discovery. Dallas: ACM Press, 2000: 21-30.
[13] Zaki M J. CARPENTER: Finding closed patterns in long biological datasets[C]//Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Washington, 2003: 413-419.
[14] Zaki M, Hsiao C. CHARM: An efficient algorithm for closed itemset mining[C]//Proceedings of the 2nd SIAM International Conference on Data Mining. Arlington: SIAM, 2002: 12-28.
[15] Khan J, Wei J. Ringner M. Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks[J]. Nat Med, 2001, 7(6): 673-679.
收稿日期:2007-11-25;修回日期:2008-01-20
基金项目:国家杰出青年科学基金资助项目(60425310);中南大学博士后基金资助项目(2008)
通信作者:李 宏(1966-),男,湖南长沙人,教授,博士后,从事数据挖掘、模式识别和信号处理工作;电话:13575892566;E-mail: lihongcsu@mail.csu.edu.cn