Calculation of free energy of Al-Cu-Li alloy under electric field

ZHANG Jian-jun(张建军)¹, WANG Yong-xin(王永欣)¹, CHEN Zheng(陈 铮)^{1, 2}, LIU Bing(刘 兵)¹

1. School of Materials Science and Engineering, Northwestern Polytechnical University,

Xi’an 710072, China;

2. State Key Laboratory of Solidification Processing, Northwestern Polytechnical University,

Xi’an 710072, China

Received 13 September 2006; accepted 10 January 2007

Abstract: Based on Thomas-Fermi model, the interior potential boundary condition with the effect of electric field was defined, the calculation method of free energy for atom cluster under electric field was established. The change of free energy of Al-Cu-Li alloy under the effect of electric field was calculated quantitatively. It is shown that: near the zero electric field and the side of positive electric field, the free energy of Cu₄LiAl₇ compound at aging temperature 460 K is higher than that of free energy at solid solution temperature 725 K, but once the negative electric field increases to certain degree there will be opposite result. Under the effect of electric field, at 725 K the free energy of Cu₄LiAl₇ is higher than that of Al-1.0%Li-4.0%Cu, and at 460 K the free energy of compound is lower than that of solid solution. When the copper content in the Al-Li-Cu solid solution is below 5%, under the effect of electric field the free energy of solid solution increases gradually with the increasing of copper content, but the increasing amplitude reduces with the increasing of copper content. The free energy of binary solid solution increases with the addition of lithium, and with the increasing of electric field intensity the free energy margin of two kinds of solid solution becomes bigger.

Key words: free energy; electric field; Thomas-Fermi model; Al-Cu-Li alloy

1 Introduction

The electric field has widely been used in materials science. It was found that the thermodynamic and kinetics behaviors of materials in electric field are different from those under the traditional temperature condition[1]. Now there is great improvement in material treatment and synthesis process using electric field[2-6]. It was found that the electric field is significant for the atom diffusion and solution. But these need proof from the energy information of microscopic atom and atom cluster. It becomes an important researching method that using mathematic model to calculate energy information of atom cluster, and it has great theoretical significance and practical value.

Thomas-Fermi(TF) model has the characteristic of elegance physics thinking and simplicity mathematics treatment, and it provides a heuristic semiclassical method to describe the electrostatic potential and the electron distribution around the atomic nucleus. In the process of modifying TFD theory model (TF model consider exchange energy), CHENG and CHENG present “quantum bag” model[7] for the investigation of the essential problem of non-van der Waal’s interaction in condensed matter—electron motion. They made a quantum mechanics analysis of the electron motion, and defined the quantum mechanics tunneling effect on electron film at the material boundary. They indicated that the boundary potential of the electron film was the important factor that was not considered before theory investigation. The calculation result of combining this conception with TFD model was in conformity with the experiment result. In this paper, this conception was combined with TF model, and was used to treat the relationship between the electric field and boundary potential. Then the effect of electric field was introduced into the internal of atom, the effect of electric field on electron density was reckoned among. So the effect of electric field on energy information of atom cluster can be calculated form electron level.

2 Model of calculation

TF model is extensively applied in molecule theory, solid theory, etc. The key problem of its application in the research of free energy in atom system is the density calculation of electrons n(r), which is also the key factor of first principle. This can be investigated by the relationship between the charge density and interior potential. The charge density is

where  p is the momentum of electrons, r is the position of electrons, and f(r, p) is the Fermi distribution function of electrons.

TF model adopts partial free electron gas approximation, the free energy of free electron gas (Eqn.(3)) can be expressed partially, and at the same time correlation can be introduced, and then integrated over the volume of the atom—all of these lead to the free energy of TF model:

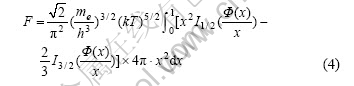
where  I_n(ξ) is Fermi function.

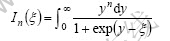
The boundary condition of TF model with temperature is

1) when r→0, U(r)→ze/r, so Φ(0)=ze²/kTr₀;

2) when r→r₀, U(r₀)=0, (dU/dr)r₀=0, so

When the atom system is not in ground state, the boundary condition of the atom will be changed accordingly. In this paper, the influence of electric field didn’t change the principal part of atom structure, namely the part of nucleus and local electron of atom, but disturbed the free electron (changed the electron density). The system described by TF model still obeys the basic relation, but the boundary condition must be modified.

  3 Boundary condition modification

The stability of system is determined by boundary condition, and the specific boundary condition determines a whole characteristic solution—eigen solution of quantum mechanics. Any system relationship in microscopic is defined strictly by boundary condition. For the particle of composing macroscopic material, the important thing is the boundary condition and making it in use. CHENG et al present an important proposition [8-10], which researched the boundary condition of electron and molecule, and then determined the system nature and macroscopic property. In this paper, the modification of boundary condition was made with reference to “quantum bag”, which was presented in modified TFD model by CHENG et al. The neutral boundary condition was modified, and the boundary condition under electric field was present.

The boundary condition of TF model with temperature in electric field was modified. Near the nucleus the potential is still given by nucleus. But near the boundary of sphere cell where r→r₀, U(r₀)→U_E. So the boundary condition of TF model with temperature in electric field is

When r→0, U(r)→ze/r, then

When r→r₀, U(r₀)=U_E, (dU/dr)r₀=0, then

On the basis of capacitor principle, the potential energy of electric field is the product of the average potential difference and charge

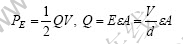
where  Q is the charge (C), V is potential difference (V), E=V/d is the intensity of electric field, ε is dielectric constant of medium, A is area of sample and electrode plate, ε is the distance between sample and electrode plate.

So the potential of electric field (boundary potential)

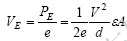is (J), the potential difference (electrode voltage) is (V).

In this paper the value of about equation parameters are that d=1 cm, A=2 cm×120 cm, and ε is the dielectric constant of air.

  4 Calculation of compound

For compound and mixture, on the basis of average atomic model, some kinds of elements compose a representative mixed atom according to the percentage of matter. Each atom demands to satisfy the mix balance conditions[11]: in the mixed materials the pressure and temperature of each atom is the same; the chemical potential of electron is the same, and the total electron counts the conservation in each atom. For these four balanced conditions, pressure and temperature are the same and must get the abundant assurance. Under invariable temperature and pressure, the interior density of different composition is uncontrollable in the mixture. Suppose that the chemical compound (or mixture) is made up of several kinds of elements, the average relative atomic mass M of the “mix” atom is

The mass fraction of the atom is W₁, W₂ and W₃; the density of mixture is ρ. Based on the theory of TF, when the volume is divided equally, the compound is equal to an “atom cell”. The Wigner-Seitz radius of the “atom cell”, namely, compound is

On the basis of basic hypothesis, R₀ is the Wigner-Seitz radius of compound and R_i is the Wigner-Seitz radius of every atom which follows the relationship as

According to the requests of mix balance condition and the above atom radius equations, through repeated iterative computation (in Ref.[11]), suitable chemical potential and a set of {R_i}, which satisfied Eqn.(9), had to be found. Then the free energy of each atom of compound can be calculated, and the free energy of compound can be calculated through volume adding method. The free energy change trend is following.

5 Results and discussion

Fig.1 shows the free energy change trend of Cu₄LiAl₇ in electric field at ageing temperature 460 K and solid solution temperature 725 K. Fig.1(a) shows the change trend of the free energy of compound with the boundary potential, and Fig.1(b) shows the change trend with the electrode voltage. From Fig.1(a), it can be found that in positive electric field the free energy of Cu₄LiAl₇ at 725 K is higher than that at 460 K, and at 725 K the free energy of Cu₄LiAl₇ increases more quickly than that at 460 K. In negative electric field, there is an intersection between the two curves, behind the intersection the free energy at 460 K is higher than that at 725 K, but before the intersection near the zero electric field the free energy of 725 K is higher than that at 460 K. For the electrode voltage, the free energy has the same change trend with the boundary potential, except that the free energy change trend with the electrode voltage becomes more slowly near the zero electric field than that of boundary potential.

Fig.1 Change of free energy of Cu₄LiAl₇ at 460 K and 725 K: (a) With boundary potential; (b) With electrode voltage

Fig.2 shows the free energy of compound Cu₄LiAl₇ and Al-1.0%Li-4.0%Cu in electric field. From Fig.2(a) it can be found that in positive field the free energy of compound is higher than that of solid solution, and in negative field there is an intersection, with the negative field increasing the free energy of compound becomes more below than that curve of solid solution. In Fig.2(b) there is the same trend. When the electrode voltage is above -500 kV, the free energy of compound is higher than that of Al-1.0%Li-4.0%Cu. Near zero electrode voltage, the compound and solid solution have some symmetry, which is the same with the experimental performance. In experiment, at 725 K Cu₄LiAl₇ doesn’t precipitate from Al-1.0%Li-4.0%Cu. It is monophase field at 725K, and in experiment, the property of solid solution has certain extent symmetry.

Fig.2 Change of free energy of Cu₄LiAl₇ and Al-1.0%Li- 4.0%Cu solid solution at 725 K: (a) With boundary potential; (b) With electrode voltage

Fig.3 shows the change trend of free energy of Cu₄LiAl₇ and Al-1.0%Li-4.0%Cu alloy in the electric field at 460 K. At this temperature the free energy of compound changes more slowly than that of alloy, and the value of free energy of compound is higher than that of alloy. This is thermodynamic proof for the ternary compound precipitating at this aging temperature. The difference between the free energy of compound and alloy becomes bigger with the increasing of electric field, and the difference on the side of the negative electric field is bigger than that of positive electric field side. The symmetry of free energy of alloy in about zero electric field is stronger than that of compound. Comparing Fig.3(a) with Fig.3(b), the curves of free energy at electrode voltage near zero electric field are more gently than that at boundary potential, but when the electric field increases to certain degree the curve becomes abrupt.

Fig.3 Change of free energy of Cu₄LiAl₇ and Al-1.0%Li- 4.0%Cu solid solution at 460 K: (a) With boundary potential; (b) With electrode voltage

Fig.4 shows the change trend of free energy of solid solution with different copper content at 725 K in the electric field. From Fig.4, it can be found that the free energy increases with the copper content increasing. The difference between curves L3 and L4 is less than the difference between curves L1 and L2, indicating that the increased amplitude reduces with the increasing of copper content. Comparing Fig.4(a) with Fig.4(b), the curves in Fig.4(b) are almost overlapped together, so the difference of free energy with electrode voltage for different copper content is less than that with boundary potential.

Fig.4 Change of free energy of solid solution with different copper contents at 725 K: (a) With boundary potential; (b) With electrode voltage

Fig.5 shows the change trend of free energy of Al-Cu-Li solid solution and Al-Cu solid solution in electric field. It can be found that the free energy of Al-Cu-Li solid solution is greater than that of Al-Cu solid solution, so the free energy of solid solution increases with the addition of Li element. And the greater the electric field intensity, the more difference between the free energy of two solid solution. This indicates that the addition of Li element increases the sensibility of solid solution to electric field.

Fig.5 Change of free energy of Al-4%Cu and Al-4%Cu-1%Li solid solution at 725 K: (a) With boundary potential; (b) With electrode voltage

Fig.6 shows the change trend of Vickers hardness of Al-Li alloy with the positive and negative electric fields. When the solid solution time is 30 min and 60 min, the Vickers hardness increases with the increasing of electric field. And the effect of positive electric field is greater than that of negative electric field, which is similar with the calculation.

Fig.6 Vickers hardness of Al-Li alloy solutionized with electric field for 30 min (a) and 60 min (b)

6 Conclusions

1) Based on Thomas-Fermi model, the calculation methods of monatomic free energy are given. The effect of electric potential on the atom interior boundary potential is established, and then the interior potential boundary condition in the electric field is defined. On the basis of these, the calculation methods of free energy of ternary compound and solid solution in the electric field have been set up.

2) Near the zero electric field and the side of positive electric field, the free energy of Cu₄LiAl₇ compound at 460 K is higher than that of free energy at 725 K, but once the negative electric field increases to certain degree there will be opposite result.

3) In the electric field, at 725 K the free energy of Cu₄LiAl₇ is higher than that of Al-1.0%Li-4.0%Cu, and at 460 K the free energy of compound is lower than that of solid solution.

4) When the copper content in the Al-Li-Cu solid solution is below 5%, under the effect of electric field the free energy of solid solution increases gradually with the increasing of copper content, but the increasing amplitude reduces with the increasing of copper content.

5) Under the effect of electric field, the free energy of binary solid solution is increased with the addition of lithium, and with the increasing of electric field intensity the free energy difference of two kinds of solid solution becomes bigger.

References

[1] ZHANG Jian-jun, CHEN Zheng, LIU Xia, WANG Yong-xin, LIU Bing, WEI Qi-long. Calculation of free energy of Al-Li-Mg alloy of TF equation [J]. Rare Metal Materials and Engineering, 2006, 35(8): 1187-1191. (in Chinese)

[2] LIU Bing, CHEN Zheng, WANG Yong-xi, WANG Xi-ning. The effect of an electric field on the mechanical properties and microstructure of Al-Li alloy containing Ce [J]. Materials Science and Engineering A, 2001, 313: 69-74.

[3] WANG Yong-xin, CHEN Zheng, LIU Bing, MA Liang, TANG Li-ying, ZHAO Yu-hong. Computer simulation of the mechanism of ordered precipitates of Al-Li alloy in external energy filed [J]. Rare Metal Materials and Engineering, 2005, 34(1): 46-50. (in Chinese)

[4] CHEN Zheng, LIU Bing, WANG Yong-xin, WEI Qi-long. Effect and phenomenological theory of electric field treatment on grain boundary strengthening [J]. Rare Metal Materials and Engineering, 2001, 30(5): 331-334. (in Chinese)

[5] KOCH C C. Experimental evidence for magnetic or electric field effects on phase transformations [J]. Materials Science and Engineering A, 2000, 287: 213-218.

[6] YANG D, CONRAD H. Influence of an electric field on the plastic deformation of polycrystalline NaCl at elevated temperatures [J]. Acta Mater, 1998, 46(6): 1963-1968.

[7] CHENG Kai-jia, CHENG Shu-yu. The analysis and calculation for internal stress of film [J]. Progress in Natural Science, 1998, 8(1): 20-29. (in Chinese)

[8] CHENG Kai-jia, CHENG Shu-yu. Importance on boundary conditions at interfaces and free surfaces of materials [J]. Rare Metal Materials and Engineering, 1998, 27(4): 189-193. (in Chinese)

[9] CHENG Kai-jia, CHENG Shu-yu. The theoretical basis of material science discussion [J]. Progress in Natural Science, 1996, 6(1): 12- 20. (in Chinese)

[10] CHENG Kai-jia, CHENG Shu-yu. The roles of minority charge carriers in the characteristics of functional materials [J]. Journal of Materials Research, 1996, 10(1): 1-6. (in Chinese)

[11] MENG Ji-jun, ZONG Xiao-ping, BAI Yun, SUN Yong-sheng, ZHANG Jing-lin. Self-consistent calculation of atomic structure for mixture [J]. Acta Physica Sinica, 2000, 49(11): 2133-2138. (in Chinese)

Foundation item: Project(50671084) supported by the National Natural Science Foundation of China; Project(2003E103) supported by Natural Science Foundation of Shaanxi Province, China

Corresponding author: ZHANG Jian-jun; Tel: +86-29-88474095; E-mail: zhangjianjun@gmail.com

(Edited by YUAN Sai-qian)