J. Cent. South Univ. (2016) 23: 370-378
DOI: 10.1007/s11771-016-3082-4
Trajectory tracking control for underactuated unmanned surface vehicles with dynamic uncertainties
LIAO Yu-lei(廖煜雷)1, ZHANG Ming-jun(张铭钧)1, 2, WAN Lei(万磊)1, LI Ye(李晔)1
1. Science and Technology on Underwater Vehicle Laboratory, Harbin Engineering University, Harbin 150001, China;
2. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: The trajectory tracking control problem for underactuated unmanned surface vehicles (USV) was addressed, and the control system took account of the uncertain influences induced by model perturbation, external disturbance, etc. By introducing the reference, trajectory was generated by a virtual USV, and the error equation of trajectory tracking for USV was obtained, which transformed the tracking problem of underactuated USV into the stabilization problem of the trajectory tracking error equation. A backstepping adaptive sliding mode controller was proposed based on backstepping technology and method of dynamic slide model control. By means of theoretical analysis, it is proved that the proposed controller ensures that the solutions of closed loop system have the ultimate boundedness property. Simulation results are presented to illustrate the effectiveness of the proposed controller.
Key words: trajectory tracking; underactuated; unmanned surface vehicle (USV); backstepping; dynamic sliding mode control
1 Introduction
Over the past decade, the control problem of underactuated unmanned surface vehicle (USV) has attracted a great deal of attentions [1-5]. The major solutions of tracking problem for underactuated USV are the methods of Lyapunov’s direct method, backstepping technique, sliding mode control, feedback linearization, robust control, switching control, etc. [4]. Some scholars used the method of feedback linearization [6], but the inversion of dynamical equation must meet a strict limited condition while its application has been so limited that it cannot ensure the stability of zero dynamics. On the contrary, the Lyapunov’s direct method does not have limitations of the above methods [7-8]. This method is used to realize the trajectory tracking. However, these methods do not take account of the strong nonlinearity or even the uncertainties coming from the movement of vehicles. REPOULIAS and PAPADOPOULOS [9] discussed the trajectory planning and tracking problems for underactuated AUV, and developed a trajectory-tracking controller by application of integral backstepping technique. Furthermore, the above-mentioned works have ignored the impact of the second damping force and the uncertainties of the model.
the problem of combined trajectory-tracking and path-following for underactuated USV with parametric modeling uncertainty was addressed [10]. By combining control law of adaptive switching with the control law based on nonlinear Lyapunov’s direct method, this work solved the global convergence problem about the system position error. Simulations validated the effectiveness of the proposed controller. On the basis of the previous studies, REYHANOGLU and BOMMER [11] proposed a trajectory tracking controller by constructing the switching feedback controller and making use of backstepping technique, which ensured the global stability of the system. This controller has an advantage of avoiding the singularity problem that may arise in the process of coordinate transformation made by USV second-order kinetic equation.
Aiming at the difficulty of the trajectory tracking for underactuated USV, a trajectory tracking controller was developed by using sliding mode control theory in Ref. [12]. The twin-propeller was used for a small USV to carry on an tank experiment, and the result showed that the USV could track a straight line and circular trajectory. For avoiding the restrictions that conventional sliding mode controller only tracks the initial state on the desired trajectory, SOLTAN et al [13] proposed a trajectory tracking controller based on the sliding mode control and ordinary differential equations (ODE)method. Simulation results showed that the underactuated USV at different initial states was able to track the desired trajectory. However, these methods only solve the position tracking problem because the orientation of USV is uncontrolled under them proposed controller. LIAO et al [4] proposed a trajectory tracking controller via backstepping technique and Lyapunov’s direct method, and system have the ultimate boundedness property. However, none of these papers take account of the system dynamic uncertainties.
Considering the trajectory tracking problem for underactuated USV with uncertain influences and the limitations of the above thesis. The trajectory tracking error equation of underactuated USV was obtained based on Ref. [4]. Aiming at the control problem of this error equation, a backstepping adaptive dynamic sliding mode controller was developed by combining backstepping technique and dynamic sliding mode control method. Proposed controller guarantees that trajectory tracking errors are ultimately bounded via Lyapunov analysis. Moreover, contrastive simulation results show that the proposed controller have good control performance and robustness.
2 Problem formulation
The motion model of a class of underactuated USV is shown in Fig. 1. Clearly, the only control inputs of the vehicle are the thrust force Fu and yaw torque Tr. Considering the impact of the nonlinear damping in mathematical model is included to cover the applications from low speed to high speed. Thus, the mathematical model of an underactuated USV moving in a horizontal plane is described as [4, 13]
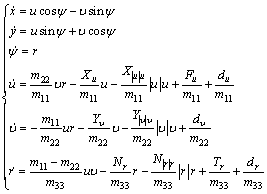 (1)
(1)
where x, y and ψ denote the position and orientation of USV in the earth-fixed frame ({E}-frame); and u, u and r are the surge, sway and yaw velocities in the body-fixed frame ({B}-frame), respectively. The parameters m11, m22 and m33 are given by vehicle inertial mass and additional mass effects; 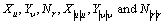 denote the linear and nonlinear hydrodynamic dampings, respectively. The unknown parameters du, du and dr denote respectively the surge, sway and yaw external disturbances caused by model perturbation, measuring noise, marine environmental disturbance, which satisfy the bounded and slow conditions:
denote the linear and nonlinear hydrodynamic dampings, respectively. The unknown parameters du, du and dr denote respectively the surge, sway and yaw external disturbances caused by model perturbation, measuring noise, marine environmental disturbance, which satisfy the bounded and slow conditions: 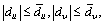
 and
and 
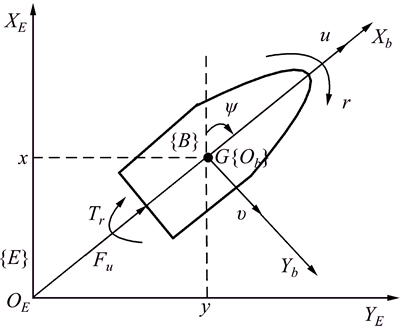
Fig. 1 Planar motion model of underactuated USV
Generally, in order to deal with the trajectory tracking control problems, the trajectory tracking control law was proposed to drive the vehicle sail along the pre-specified feasible trajectory. This trajectory specifies the expectational position and orientation of the vehicle in every moment, and it has to meet the dynamic equations of the vehicle. REPOULIAS and PAPADOPOULOS [9] developed a trajectory planning method via the dynamic equation of underactuated AUV, which can also be applied to the USV. This method can provide the reference speed in body-fixed frame based on underactuated USV nominal kinetic equation. Moreover, if the mathematical model of USV motion does not have any uncertainty or its uncertainty is small, this planning approach will be very effective. However, if the mathematical model has large uncertainties, the reference speed and heading angle via the nominal kinetic equation are different from those of the real USV dynamics equation, then this planning approach will be invalid [4]. Based on the above methods, in order to simplify the reference kinetic equation, a simplified planning method is developed by neglecting the influence of the sway velocity [15]. However, if the curvature of reference trajectory is truly large, sway velocity should not be ignored. Therefore, this planning method cannot be applied to the trajectory tracking problems with large curvature.
LIAO et al [4] proposed a planning method combines the advantage of the above two methods. Namely, for desired trajectory (xd, yd, ψd), the surge and yaw reference velocities ud, rd are given by the kinematic equations, which avoid the uncertain influences of the kinetic equation. However, the sway velocity ud is given based on virtual USV, which considers the impact of the USV dynamics. Motivated by Refs. [4, 8], the reference trajectory is generated by a virtual USV as
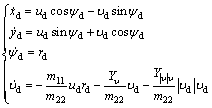 (2)
(2)
where all variables of Eq. (2) have the same meaning as in Eq. (1). Moreover, considering the following assumptions [8]:
Assumption 1: The reference velocities ud, rd are bounded and differentiable with bounded derivatives 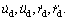
Assumption 2: The reference velocities ud, rd meet one of the following conditions:
C1.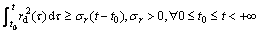
C2.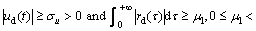
Condition C1 denotes the tracking problem of circular path. Condition C2 covers the tracking problem of straight-line or way-point. The position and orientation errors are defined as x-xd, y-yd, ψ-ψd in the {E}-frame, we have
 (3)
(3)
Apparently, the convergence of (xe, ye, ψe) to the zero can ensures convergence of x-xd, y-yd, ψ-ψd. The velocity tracking errors are defined as ue=u-ud, ue=u-ud, re=r-rd in the {B}-frame. Differentiating both sides of Eq. (3) along solutions of Eqs. (1) and (2), and substituting Eqs. (1) and (2) into it. Then, the trajectory tracking error equation of underactuated USV is obtained as
 (4)
(4)
It is obvious that the tacking problem of underactuated USV is equivalent to stabilizing Eq. (4), which is an uncertain nonlinear system with dual-input and three-output. Therefore, the control objective is formally expressed as: designing a control law u=(Fu, Tr) to ensure that the system tracking error x=(xe, ye, ψe, ue, ue, re) can converge to an arbitrarily small neighborhood near zero.
3 Controller design
The sliding mode control method has been widely used in nonlinear control systems, but it inevitably contains the “chattering” problem. However, the “chattering” cannot be eliminated since it means the loss of the robustness from the variable structure control to the model perturbation and external disturbance. Therefore, the “chattering” can only be weaken to a certain extent for the sliding mode control. As an effective way to eliminate chattering, dynamical sliding mode control (DSMC) is applied to nonlinear systems such as the robots, arms, nuclear power systems, etc. [16-18].
In recent years, some researchers have already applied backstepping technique to the control problem of underactuated marine launch systems [19-20]. By the introduction of intermediate controller, backstepping makes the controller design procedural and systematical. It is a very effective method for sliding mode control for non-matching uncertainties and non-minimum phase systems.
Therefore, for the controller design problem of the Eq. (4), a backstepping adaptive dynamical sliding mode controller (BADSMC) is proposed based on backstepping technique with adaptive technology and DSMC. The proposed controller has good robustness and adaptive capacity by combining the advantages of backstepping and DSMC.
3.1 Backstepping adaptive dynamic sliding mode controller design
The controller design consists of four steps as follows.
Step 1: Stabilizing subsystem (xe, ye)
Considering the subsystem (xe, ye), select the virtual control inputs as (ue, ue). Define Lyapunov function as
 (5)
(5)
Differentiating V1 along the solutions of Eq. (4) yields
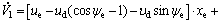
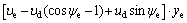 (6)
(6)
The desired control inputs 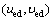 are selected as
are selected as
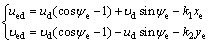 (7)
(7)
where k1 and k2 are positive constants. Substituting Eq. (7) into Eq. (6) yields
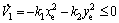 (8)
(8)
However, (ued, ued) are not the actual control inputs. Thus, the error variables are define as
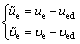 (9)
(9)
Substituting 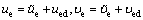 into Eq. (6) yields
into Eq. (6) yields
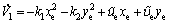 (10)
(10)
Next, the subsystem 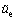 is discussed.
is discussed.
Step 2: Stabilizing subsystem 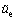
The Lyapunov function is defined as
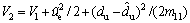 (11)
(11)
where 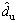 is the estimation value of the uncertain impact du.
is the estimation value of the uncertain impact du.
Differentiating 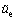 along the solution of Eq. (9) yields
along the solution of Eq. (9) yields
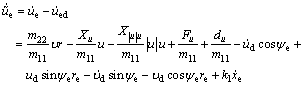
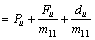 (12)
(12)
where 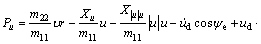
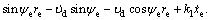
Differentiating V2 along the solutions of Eqs. (4) and (9) yields
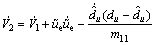
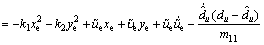 (13)
(13)
The switching function is selected as
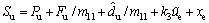 (14)
(14)
where k3 is a positive constant. Substituting Eq. (14) into Eq. (12) yields
 (15)
(15)
Substituting Eq. (15) into Eq. (13) yields
 (16)
(16)
We let  and make a time derivation of Su, then we obtain
and make a time derivation of Su, then we obtain
 (17)
(17)
The Lyapunov function is defined as
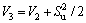 (18)
(18)
Differentiating V3 along the solutions of Eqs. (4) and (14) yields
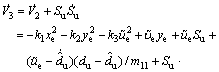
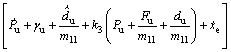 (19)
(19)
The following dynamical sliding mode control law γu is designed
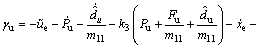
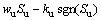 (20)
(20)
where wu and ku are positive constants. Substituting Eq. (20) into Eq. (19) yields
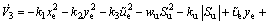
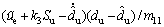 (21)
(21)
By choosing the adaptive law of uncertainty term du as
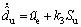 (22)
(22)
Substituting Eq. (22) into Eq. (21) yields
 (23)
(23)
Step 3: Stabilizing subsystem 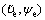
Considering the subsystem 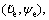 the virtual control input is defined as re. Define Lyapunov function as
the virtual control input is defined as re. Define Lyapunov function as
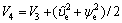 (24)
(24)
Differentiating 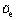 along the solution of Eq. (9) yields
along the solution of Eq. (9) yields
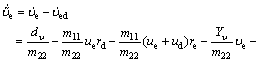
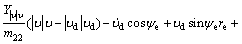
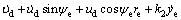 (25)
(25)
Differentiating V4 along the solutions of Eqs. (4) and (9) yields
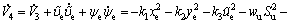
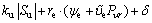 (26)
(26)
where in order to facilitate the expression of subsequent controller design, we define
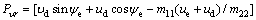 ,
,
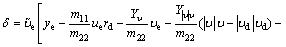
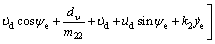
By choosing the desired control input as
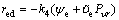 (27)
(27)
where k4 is a positive constant. Substituting Eq. (27) into Eq. (26) yields
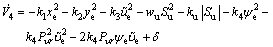
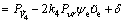 (28)
(28)
where 
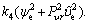
However, red is not the actual control input. Then, the error variable is define as
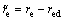 (29)
(29)
Substituting 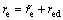 into Eq. (26) yields
into Eq. (26) yields
 (30)
(30)
Step 4: Stabilizing subsystem 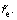
Differentiating 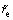 along the solution of Eq. (29) yields
along the solution of Eq. (29) yields
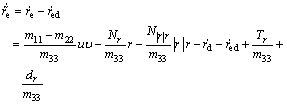
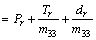 (31)
(31)
where 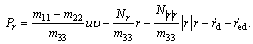
The switching function is selected as
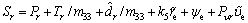 (32)
(32)
where k5 is a positive constant. Substituting Eq. (32) into Eq. (31) yields
 (33)
(33)
Lyapunov function is defined as
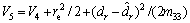 (34)
(34)
Differentiating V5 along the solutions of Eqs. (4) and (29) yields
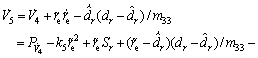
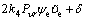 (35)
(35)
We define 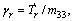 and make a time derivation of Sr, then we obtain
and make a time derivation of Sr, then we obtain
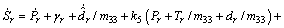
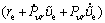 (36)
(36)
Lyapunov function is defined as
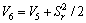 (37)
(37)
Differentiating V6 along the solutions of Eqs. (4) and (32), and substituting Eq. (33) into it yields
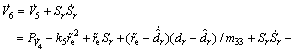
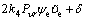 (38)
(38)
The following dynamical sliding mode control law γr is designed
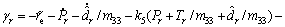
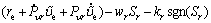 (39)
(39)
where wr, kr are positive constants. Substituting Eq. (39) into Eq. (38) yields
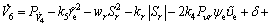
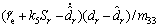 (40)
(40)
By choosing the adaptive law of uncertainty term dr as
 (41)
(41)
Substituting Eq. (41) into Eq. (40) yields
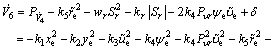
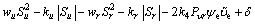 (42)
(42)
The stability analysis of control system is presented as follows.
3.2 Stability analysis
Considering the worst conditions, we have
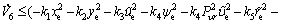
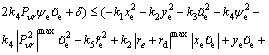
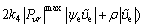 (43)
(43)
where 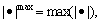 and ρ is the expressed as
and ρ is the expressed as
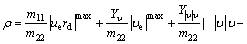
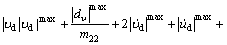
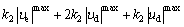 (44)
(44)
In order to deal with the uncertain variables of positive and negative symbols in Eq. (43), the Young’s inequality is used for algebraic processing. The worst cases caused by these uncertain variables are considered in the process. By the Young’s inequality, we obtain
 (45)
(45)
where ε1, ε2, ε3 are positive constants.
According to the above analysis, Eq. (43) is refreshed to be
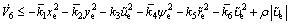 (46)
(46)
where the expressions of 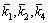 and
and 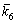 are
are
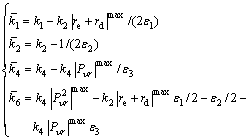 (47)
(47)
It is obvious that if the right positive parameters k1, k2, k4, ε1, ε2 and ε3 are choosed, then 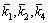 and
and 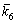 are assured positive constants. The system state variables of Eq. (4) are expressed as
are assured positive constants. The system state variables of Eq. (4) are expressed as 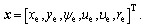
Selecting 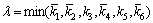 and 0<θ<1, Eq. (46) becomes
and 0<θ<1, Eq. (46) becomes
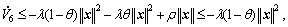
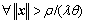 (48)
(48)
According to the Lemma 9.2 in Ref. [21], it is proved that there exists a certain limited time τ, the system state of Eq. (4) satisfies
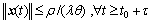 (49)
(49)
In the function of control laws Eqs. (20), (39) and adaptive laws Eqs. (22), (41), the trajectory tracking errors 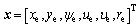 will have global convergence by remaining in a limited region around zero, the size of which can arbitrarily be diminished by increasing the control gain
will have global convergence by remaining in a limited region around zero, the size of which can arbitrarily be diminished by increasing the control gain 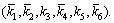 Therefore, the trajectory tracking problem for underactuated USV with uncertain impacts has already been solved.
Therefore, the trajectory tracking problem for underactuated USV with uncertain impacts has already been solved.
Theorem 1: Selecting the suitably positive parameters  to assure that
to assure that 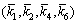 are positive constants, and choose positive parameters
are positive constants, and choose positive parameters 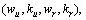 the solutions of closed-loop control system defined by Eq. (4) are ultimate boundedness in function of control laws Eqs. (20) and (39) and adaptive laws Eqs. (22) and (41).
the solutions of closed-loop control system defined by Eq. (4) are ultimate boundedness in function of control laws Eqs. (20) and (39) and adaptive laws Eqs. (22) and (41).
Theorem 1 is already proved by the controller design and analysis of stability above.
4 Numerical simulations
Simulation results are present to verify the effectiveness of our proposed method. The following nominal model parameters of an USV are selected [20]
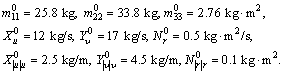
4.1 trajectory tracking of nominal model
The condition C1 in Assumption 2 is discussed. The reference trajectory is made by the virtual USV with the initial conditions as:  and the desired speeds are choose as: ud=1 m/s, rd=10 °/s. Therefore, the reference trajectory is a circular trajectory. Initial system states are selected as:
and the desired speeds are choose as: ud=1 m/s, rd=10 °/s. Therefore, the reference trajectory is a circular trajectory. Initial system states are selected as: 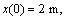 y(0)= -2 m,
y(0)= -2 m, 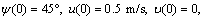 r(0)=0, and considering propeller saturation constraint conditions: -30 N≤Fu≤30 N, -2 N·m≤Tr≤2 N·m. The parameters of the proposed BADSMC are selected as k1=0.5, k2=0.4, k3=0.3, k4=0.2, k5=1, wu=10, wr=2, ku=0.01, kr=0.01.
r(0)=0, and considering propeller saturation constraint conditions: -30 N≤Fu≤30 N, -2 N·m≤Tr≤2 N·m. The parameters of the proposed BADSMC are selected as k1=0.5, k2=0.4, k3=0.3, k4=0.2, k5=1, wu=10, wr=2, ku=0.01, kr=0.01.
According to the nominal model, by setting the uncertain impacts: 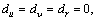 the simulation test is done. The simulation results are shown in Figs. 2-4.
the simulation test is done. The simulation results are shown in Figs. 2-4.
For the USV sailing in the wide water, the straight- line tracking is often used. Because the straight-line tracking is a simple form of the curve trajectory tracking, the proposed method can be apparently applied therein. As space is limited, it will not be discussed here.
Figure 2 shows that the BADSMC drives the USV fast track on the desired circular trajectory, hence, the task of trajectory tacking is completed with good dynamic performance. Figures 3 and 4 show that the system states converge rapidly, smoothly without overshoot in the function of BADSMC. The control outputs have not the “chattering” phenomenon, which avoids harmful mechanical wear and is easy to implement in engineering.
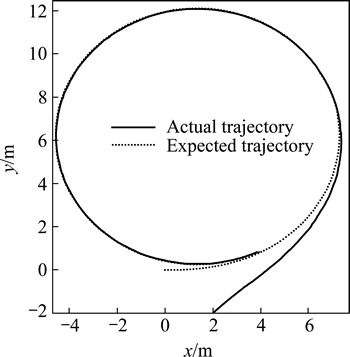
Fig. 2 Motion trajectory of USV under nominal model
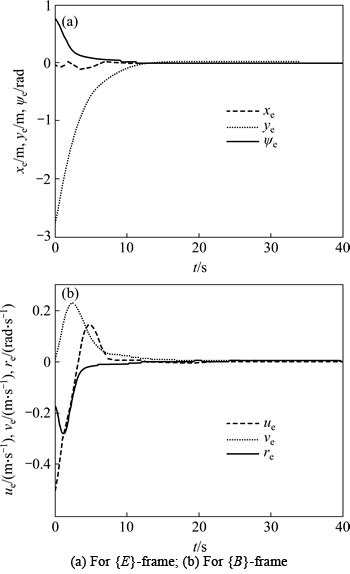
Fig. 3 Response curves of system state variables under nominal model:
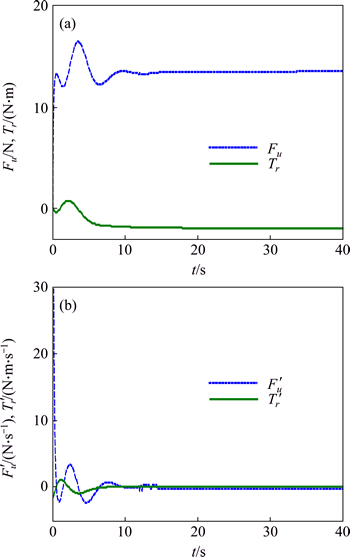
Fig. 4 Response curves of control force (a) and torque (b) under nominal model
4.2 trajectory tracking under dynamic influences
This section, the trajectory tracking problem with dynamic uncertainties is discussed in order to validate the control performance and robustness of our proposed method. Assuming the actual model has a parameter perturbation not more than 20%, without the loss of generality, an extreme situation is selected in the simulation, and the following model parameters of actual USV are given
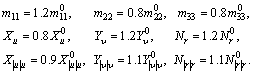
From the anterior simulation results under nominal model, the maximum of surge, sway and yaw accelerations are obtained as: 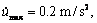
 Hence, setting external disturbance force with the same level of
Hence, setting external disturbance force with the same level of 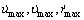 as follows:
as follows:
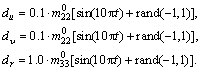
The simulation test was done under the above uncertain influences. Simulation results are shown in Figs. 5-7.

Fig. 5 Motion trajectory of USV under dynamic influences
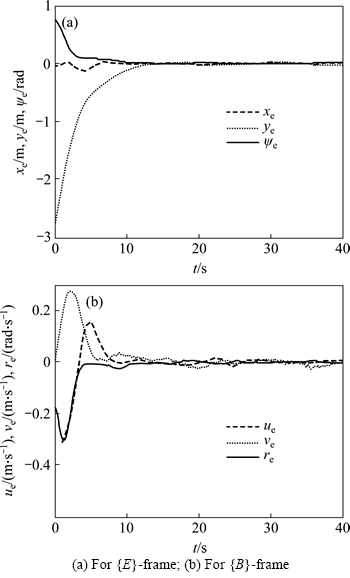
Fig. 6 Response curves of system state variables under dynamic influences:
Figures 5 and 6 show that the BADSMC can similarly drive the trajectory tracking errors quickly converge to zero. Therefore, it is obvious that the USV with dynamic influences can track the desired trajectory. Figure 7 shows that the oscillation of control force (torque) is very small, which profited from the control derivative information output of the DSMC method, instead of directly output control itself, then integral control becomes smoother. Moreover, the output of system states is smooth with no chattering, which keep the same control performance with the nominal model. It is obvious that the proposed BADSMC is not sensitive to the uncertain impacts, thereby with strong robustness.
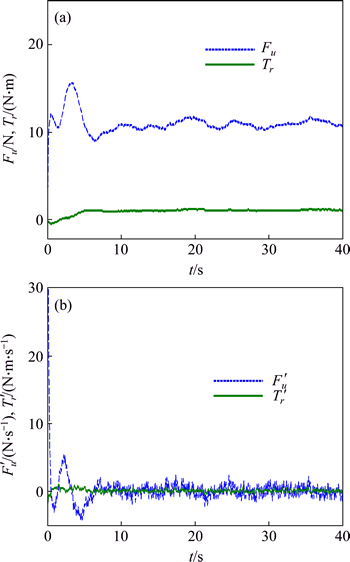
Fig. 7 Response curves of control force and torque under dynamic influences
5 Conclusions
1) The reference trajectory is generated by the virtual USV to obtain the trajectory tracking error equation, which transform the tracking problem of underactuated USV into the stabilizing problem of trajectory tracking error equation. Moreover, this equation is an uncertain nonlinear system with dual-input and three-output.
2) A backstepping adaptive dynamical sliding mode controller (BADSMC) is proposed by combining backstepping with DSMC method and the adaptive technique. Moreover, theoretical analysis shows that the solutions of closed loop system are ultimate boundedness in the function of proposed controller.
3) Simulation results show that the BADSMC is not sensitive to the uncertainties, and with good adaptive and robustness performance.
References
[1] ASHRAFIUON H, MUSKE K R, MCNINCH L C. Review of nonlinear tracking and setpoint control approaches for autonomous underactuated marine vehicles [C]// Proceedings of the 2010 American Control Conference. Baltimore, USA: IEEE, 2010: 5203-5211.
[2] DO K D, PAN J. Underactuated ships follow smooth paths with integral actions and without velocity measurements for feedback: theory and experiments [J]. IEEE Transactions on Control System Technology, 2006, 14(2): 308-322.
[3] DO K D, PAN J, JIANG Z P. Robust and adaptive path following for underactuated autonomous underwater vehicles [J]. Ocean Engineering, 2006, 31(16): 1967-1997.
[4] LIAO Yu-lei, SU Yu-min, CAO Jian. Trajectory planning and tracking control for underactuated unmanned surface vessels [J]. Journal of Central South University, 2014, 21(2): 540-549.
[5] LIAO Yu-lei, ZHANG Ming-Jun, WAN Lei. Serret-Frenet frame based on path following control for underactuated unmanned surface vehicles with dynamic uncertainties [J]. Journal of Central South University, 2015, 22(1): 214-223.
[6] DO K D. Universal controllers for stabilization and tracking of underactuated ships [J]. Systems & Control Letters, 2002, 47(4): 299-317.
[7] LEFEBER E, PETTERSEN K Y, NIJMEIJER H. Tracking control of an underactuated ship [J]. IEEE Transactions on Control Systems Technology, 2003, 11(1): 52-61.
[8] AL-HIDDABI S A, MCCLAMROCH N H. Tracking and maneuver regulation control for nonlinear nonminimum phase systems: application to flight control [J]. IEEE Transactions on Control Systems Technology, 2002, 10(6): 780-792.
[9] REPOULIAS F, PAPADOPOULOS E. Planar trajectory planning and tracking control design for underactuated AUVs [J]. Ocean Engineering, 2007, 34(2): 1650-1667.
[10] AGUIAR A P, HESPANHA J P. Trajectory-tracking and path-following of underactuated autonomous vehicles with parametric modeling uncertainty [J]. IEEE Transactions on Automatic Control, 2007, 52(8): 1362-1379.
[11] REYHANOGLU M, BOMMER A. Tracking control of an underactuated autonomous surface vessel using switched feedback [C]// Proceedings of the 32nd Annual Conference on IEEE Industrial Electronics. Paris, France: IEEE, 2006: 3833-3838.
[12] ASHRAFIUON H, MUSKE K R. Sliding-mode tracking control of surface vessels [J]. IEEE Transactions on Industrial Electronics, 2008, 55(11): 4004-4011.
[13] SOLTAN R A, ASHRAFIUON H, MUSKE K R. State-dependent trajectory planning and tracking control of unmanned surface vessels [C]// Proceedings of the 2009 American Control Conference. Missouri, USA: IEEE, 2009: 3597-3602.
[14] FOSSEN T I. Marine control systems: guidance, navigation, and control of ships, rigs and underwater vehicles [M]. Trondheim, Norway: Marine Cybernetics, 2002.
[15] BI Feng-yang. Research on nonlinear robust control strategies of underactuated autonomous underwater vehicle [D]. Harbin, China: Harbin Institute of Technology, 2010. (in Chinese)
[16] DAVILA J, POZNYAK A. Dynamic sliding mode control design using attracting ellipsoid method [J]. Automatica, 2011, 47(1): 1467-1472.
[17] SUNGSOO N, LEE B, CHOO J P M. Robust dynamic sliding mode control of a rotating thin-walled composite blade [J]. Journal of Aerospace Engineering, 2011, 24(3): 298-308.
[18] ANSARIFAR G R, DAVILU H, TALEBI H A. Gain scheduled dynamic sliding mode control for nuclear steam generators [J]. Progress in Nuclear Energy, 2011, 53(1): 651-663.
[19] REFSNES J E, SRENSEN A J, PETTERSENM K Y. Model-based output feedback control of slender-body underactuated AUVs: theory and experiments [J]. IEEE Transactions on Control Systems Technology, 2008, 16(5): 930-946.
[20] DO K D, PAN J. Robust path-following of underactuated ships: theory and experiments on a model ship [J]. Ocean Engineering, 2006, 33(10): 1354-1372.
[21] KHALIL H K. Nonlinear systems (3rd ed) [M]. Upper Saddle River, New Jersey, USA: Prentice-Hall, 2002.
(Edited by DENG Lü-xiang)
Foundation item: Project(51409061) supported by the National Natural Science Foundation of China; Project(2013M540271) supported by China Postdoctoral Science Foundation; Project(LBH-Z13055) Supported by Heilongjiang Postdoctoral Financial Assistance, China; Project(HEUCFD1403) supported by Basic Research Foundation of Central Universities, China
Received date: 2015-02-09; Accepted date: 2015-06-10
Corresponding author: LIAO Yu-lei, PhD, lecturer; Tel: +86-18045623860; E-mail: liaoyulei@hrbeu.edu.cn