DOI: 10.11817/j.issn.1672-7207.2020.01.007
二齿差摆盘式活齿传动的接触力学
贺亚博,梁尚明,杨勇
(四川大学 机械工程学院,四川 成都,610065)
摘要:针对二齿差摆盘式活齿传动系统在高速重载的工作条件下容易产生局部的挤压变形或疲劳磨损等问题,依据二齿差活齿传动的对称性,对二齿差摆盘式活齿传动系统的模型进行简化,并运用有限元分析方法计算各零件在接触点附近的等效应力。研究反映传动动态过程的活齿相位以及活齿振幅、活齿半径、沟曲率半径系数等参数对接触应力的影响。应用接触力学的经典理论,研究接触点次表面不同类型应力的分布状态,并且在静强度校核的基础上对系统进行疲劳分析,计算接触疲劳寿命,确定系统可能疲劳失效的危险区域。研究结果表明:各零件的应力均集中在接触点附近的微小区域内,分布状态符合预期,属于典型的接触问题,同时验证了差异化网格划分的合理性;振幅增大、活齿半径增大、沟曲率半径系数减小均会导致接触应力最大值的减小,反之亦然。
关键词:摆盘式活齿传动;二齿差;接触力学;有限元;相位
中图分类号:TH123 文献标志码:文献标识码:A
文章编号:1672-7207(2020)01-0049-10
Contact mechanics of two-tooth-difference oscillating-disc movable teeth transmission
HE Yabo, LIANG Shangming, YANG Yong
(School of Mechanical Engineering, Sichuan University, Chengdu 610065, China)
Abstract: For the two-tooth-difference oscillating-disc movable teeth transmission system, it is easy to produce local crush deformation or fatigue wear under the working conditions of high speed and heavy load. According to the symmetry of the two-tooth-difference movable teeth transmission, the model of the two-tooth-difference oscillating-disc movable teeth transmission system was simplified, and the equivalent stress of each part near the contact point was calculated by the finite element analysis method. The phase of the movable tooth reflecting the dynamic process of the transmission, as well as the influence of the parameters of the movable tooth amplitude, the movable tooth radius and the groove curvature radius coefficient on the contact stress were studied. The classical theory of contact mechanics was used to study the distribution of different types of stress on the surface of the contact point. And based on the static strength check, the system was analyzed for its fatigue, contact fatigue life and the danger area of its pessible fatigue failure. The results show that the stress of each part is concentrated in the tiny area near the contact point, and the distribution state is in line with the expectations. It is a typical contact problem, and the rationality of differential meshing is verified. The increase of amplitude, the increase of the radius of the movable tooth, and the decrease of the radius of curvature of the groove all lead to the decrease of the maximum contact stress, and vice versa.
Key words: oscillating-disc movable teeth transmission; two-tooth-difference; contact mechanics; finite element; phase
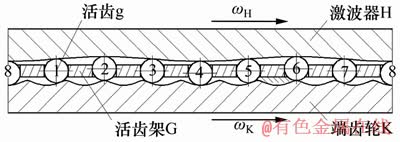
图1 二齿差摆盘式活齿传动的传动原理图
Fig. 1 Transmission principle diagram of two-tooth-difference oscillating-disc movable teeth transmission

图2 二齿差摆盘式活齿传动的三维模型
Fig. 2 Three-dimensional model of two-tooth-difference oscillating-disc movable teeth transmission
活齿传动属于行星齿轮传动的一种特殊形式,具有结构紧凑、传动比变化范围大、承载能力强和适用范围广等突出特点,近些年与其相关的研究及应用越来越多。摆盘式活齿传动作为一种新型活齿传动,相较于原有的活齿传动类型如具有代表性的摆动活齿传动、摆杆活齿传动等,其创新之处在于采用了轴向激波的形式,由此带来径向尺寸的大幅缩减,使其能够适用于径向空间较小的工作环境[1-3]。目前,对摆盘式活齿传动的研究仍然较少,原因是其偏心摆盘所造成的力偶不平衡问题与载荷不平衡问题始终难以有效解决,导致其实用性特别是高速工作条件下的稳定性受到影响[4-7]。对于二齿差摆盘式活齿传动,由于活齿与激波器及端齿轮之间均是以高副相联接,传动过程中各啮合点处的受力较为集中,在高速重载的工作条件下容易产生局部的挤压变形或疲劳磨损,影响系统的工作性能甚至使部分零件失效破坏,因此,必须予以重点关注。随着工业技术的不断发展以及活齿传动的推广应用,二齿差摆盘式活齿传动必将面对更多复杂严苛的工况条件,故而对其接触区域的强度分析具有十分重要的意义。因此,本文作者运用有限元分析方法和接触力学的经典理论对传动系统进行分析,得出各参数对接触应力的影响和确定系统可能疲劳失效的危险区域。
1 二齿差摆盘式活齿传动的接触应力有限元分析
1.1 三维模型的建立及传动原理
图1所示为二齿差摆盘式活齿传动的传动原理图。从图1可以看出:活齿1,2,3和4与活齿5,6,7和8的运动状态一一对应,完全相同,这是由二齿差活齿传动的对称激波特性决定的。在活齿1,2,3和4中,活齿1和2处于工作过程,活齿3和4处于复位过程,并且在活齿2恰好进入啮合状态的同时活齿4刚好啮出。
图2所示为二齿差摆盘式活齿传动的三维模型。对于二齿差摆盘式活齿传动这样的对称性传动系统,在进行有限元分析时,完全可以对其进行拆分,忽略对称重复的部分,以此大幅节省运算资源。由于处于复位过程的活齿接触应力较小,因此,完全可以只取处于工作过程的活齿1和2所在的1/4扇形区域部分进行研究。
为了能够分别观察活齿1及活齿2与激波器及端齿轮的接触状态,将激波器、端齿轮及活齿架拆分成多实体组件。组件中的各个实体在划分网格及计算时均被视作整体,而在提取结果时又相互独立,可以分别观察。完成分割后的状态如图3所示。其中活齿1位于左侧,已经啮入并完成一半的工作过程,活齿2位于右侧,处于刚刚啮入的位置。
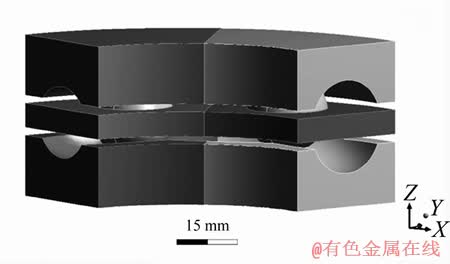
图3 二齿差摆盘式活齿传动的简化模型
Fig. 3 Simplified model of two-tooth-difference oscillating-disc movable teeth transmission
1.2 材料属性的设置
本文将所有零件的材料均选为轴承钢GCr15,其物理参数见表1。
表1 GCr15的物理参数
Table 1 Physical parameters of GCr15

1.3 网格的划分
在有限元分析中,网格尺寸会直接影响求解精度。通常情况下,网格划分越细,所求结果越接近真实值,但运算量和求解时间会相应增大[8]。由于在接触力学研究中,接触点附近区域的受力情况才具有分析价值,因此,网格的划分完全可以采用整体粗分而对关键位置细化加密的方式,以期在达到求解精度的同时尽可能节省求解时间。
综合以上分析,对二齿差摆盘式活齿传动模型的网格划分方式如下:
激波器、端齿轮及活齿采用四面体网格划分算法,活齿架采用六面体网格划分算法。
最终模型的网格划分如图4所示。从图4可以看出:网格划分效果与设计预期较为符合,粗中有细,重点突出,且网格之间过渡平缓。

图4 网格划分细节图
Fig. 4 Grid detailing
1.4 仿真环境的设置
根据二齿差摆盘式活齿传动的实际工作状况,参考同类活齿传动的载荷数据[9],并结合模型尺寸,施加如下边界条件:
对活齿架外圈施加固定约束,约束其上节点的所有自由度,模拟活齿架与机架的固定联接。
对端齿轮内孔施加固定约束,模拟输出轴被锁死的状态。
对激波器内孔施加柱面约束,并将旋转自由度打开,仅约束轴向位移及径向位移的自由度,使激波器能够自由旋转以传递转矩。
对端齿轮及激波器的外端面施加无摩擦约束,约束其轴向位移的自由度,模拟推力轴承的支撑。
对1/4圈激波器内孔施加10 kN·mm的转矩。
对于非线性问题的求解,通常还应将大变形选项打开。打开大变形后,求解器在迭代计算时每一子步均会根据前一子步的模型尺寸构造刚度矩阵,然后进行求解计算,即刚度矩阵会随着求解的进行不断更新,这样计算出的结果更加接近真实值。
1.5 计算结果的分析
计算完成后,可根据分析的需要对各个实体分别提取不同的计算结果。Von Mises等效应力综合考虑了各独立的正应力与切应力的共同影响,具有比较大的参考意义,因此对活齿1、活齿2以及与二者相接触的所有子实体(暂命名为激波器1、激波器2、端齿轮1、端齿轮2、活齿架1、活齿架2)分别提取等效应力的计算结果,部分零件的应力云图见图5。
从图5可以看出:各个零件的应力分布状态基本符合预期,主要集中在接触点附近的微小椭圆区域内,由此可以证实前文采用的网格划分方法是准确而高效的。不难发现,相对于其他零件,活齿架1的接触应力较小,仅为27.457 MPa;接触应力最大值出现在活齿1与激波器1的接触点,达到728.27 MPa。
在有限元分析中,若要确保计算结果的准确,需要不断细化网格直至计算结果收敛于一个定值,实际应用中通常在2次计算结果的相对变化率足够小时(常取为5%)即认为该结果已收敛。
本文通过对接触区域进一步添加网格细化的方式,不断提高网格细化等级,直至各计算结果均收敛,收敛过程见表2,最终细化等级为3时接触区域网格截面效果如图6所示。
表2 各零件的应力收敛过程
Table 2 Stress convergence process of each part MPa
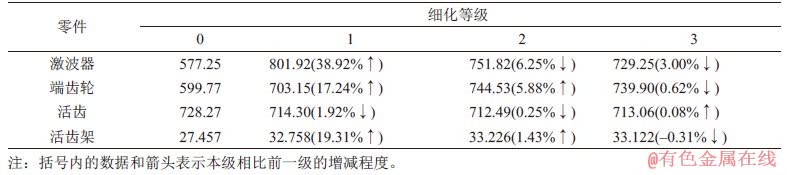
对比观察不难发现:激波器、端齿轮与活齿架的应力在网格细化后均有明显增幅,而活齿的应力则基本不变。可见对于接触问题,不同区域、不同接触状态均可能影响接触应力的分布状况与集中程度,进而导致实际所需的网格精度并不相同。由此说明网格的细化与结果的收敛对于精确求解关键位置的应力是十分必要的。
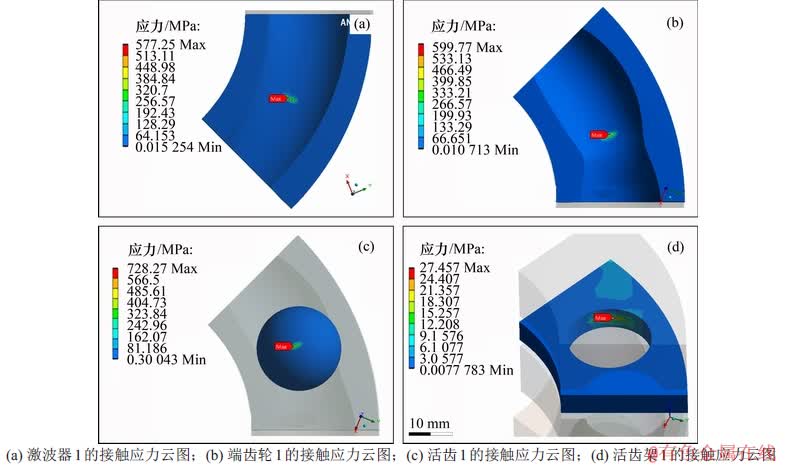
图5 各零件接触应力云图
Fig. 5 Contact stress cloud diagram of each part
以上分析均是针对各零件处于当前特定的接触状态而言的。实际工作中,各零件的接触状态是不断变化的,这将导致各零件的接触应力也发生相应改变。因此,有必要对活齿工作过程中的多个相位予以分别建模求解,以掌握各个零件在动态工作过程中的应力变化情况。
2 活齿相位对接触应力的影响
在上述二齿差摆盘式活齿传动简化模型中,将活齿恰好啮入时的相位设为0 rad(即φ=0 rad),则在相位由0~π rad的变化过程中,活齿恰好完成整个工作过程,而激波器和端齿轮转过的角度分别为90°和18°。现将这一过程12等分,依旧采用前文所述方法对处于不同活齿相位时的系统进行建模计算。通过在Pro/E中对装配体直接进行调整与剪切,可以快速建立上述各模型。又由于活齿1与活齿2的相位差恰好为π/2 rad,求解一次即可得到2个结果,因此,实际上只需对前7个相位进行建模计算,这大大减少了计算工作量。记录所有零件在各相位的接触应力,通过Origin的曲线拟合功能绘制如图7所示。
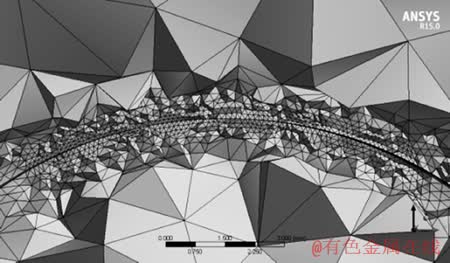
图6 接触区域的网格细化效果图
Fig. 6 Grid refinement effect of contact area
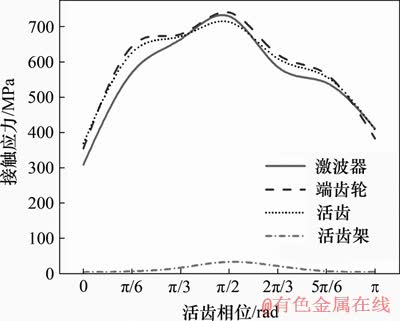
图7 接触应力随活齿相位变化图
Fig. 7 Contact stress versus active tooth phase change
从图7可以看出:在活齿的一个完整工作过程中,活齿架的应力相对其他零件始终较小;各零件的最大应力随活齿相位而变化的总体趋势都是先增大后减小,最大值均出现在φ=π/2 rad处,这与先前学者关于其他类型活齿传动的研究结果较为一致[10-11]。
以上工作对二齿差摆盘式活齿传动系统在传动过程中各零件的接触应力的变化情况进行了初步探究,并总结出一套具有针对性的快速有效的有限元分析方法(局部的网格细化、模型的对称性简化、利用组件功能一求多解),这使得后文中大量的有限元计算成为可能。
3 参数对接触应力的影响
由Hertz理论可知:在材料不变的情况下,影响接触应力的主要因素是接触点的法向载荷与主曲率。对于活齿传动系统,在传递转矩不变的情况下,法向载荷与主曲率均由齿面形状决定。考虑到参数R与i对系统的影响较大(分度圆半径R决定系统的径向尺寸,i为传动比),两者在实际工况中通常为提前设计好的恒定值,调整空间有限。沟曲率半径系数f是轴承设计中的重要参数,定义为滚道曲率半径与滚动体直径的比值,表征着滚动体与滚道接触的密合程度,通常的取值范围为0.51~0.56[12-14]。在二齿差摆盘式活齿传动中,参数f对端齿轮及激波器的空间结构有较大影响,在设计时具有一定的参考价值。
综上所述,本文采用控制变量法逐一分析参数活齿振幅A、活齿半径r、沟曲率半径系数f对二齿差摆盘式活齿传动中各零件接触应力的影响。由于活齿架在传动过程中的接触应力始终较小,故后文中不再予以讨论。
3.1 活齿振幅对接触应力的影响
图8所示为活齿振幅A对二齿差摆盘式活齿传动中各零件在整个传动过程中的接触应力的影响。从图8可知:图8中各图线相互交叉的情况较多,说明A对接触应力的影响较为复杂。归纳后发现如下特点:在图像中部区域即φ=π/2 rad附近,A与各零件的接触应力基本呈负相关;在图线接近两端的过程中,A对接触应力的影响逐渐下降,表现为图线收拢直至相交;在图像两端,A与各零件的应力关系并不相同,在φ=0 rad处与激波器呈负相关而与端齿轮及活齿呈正相关,在φ=π rad处与端齿轮呈负相关而与激波器及活齿呈正相关。
分析原因是:A在不同相位对接触应力的影响机理不同。在φ=π/2 rad附近区域,A对激波器及端齿轮在接触点附近的导槽斜率有较大影响,而对接触点的主曲率则影响较小,故前者可能是影响接触应力的主要因素。在φ=0 rad及φ=π rad附近,A对接触点处导槽斜率的影响较小,对主曲率则有较大影响,致使后者成为影响接触应力的主要因素。
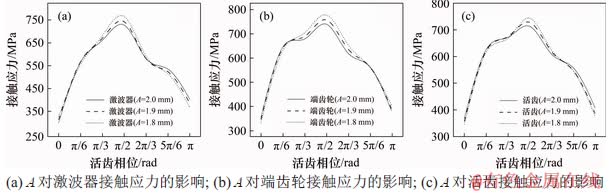
图8 A对各零件接触应力的影响
Fig. 8 Effect of A on contact stress of each part
3.2 活齿半径对接触应力的影响
图9所示为活齿半径r对二齿差摆盘式活齿传动中各零件在整个传动过程中的接触应力的影响。从图9可知:图9中各图线没有出现相互交叉的情况,说明r对接触应力的影响情况比较简单。不难看出:各零件在不同相位时的接触应力均与r呈负相关。
分析原因是:活齿半径r的变化改变了接触点附近活齿一侧的主曲率,使之成为影响接触应力的主要因素。
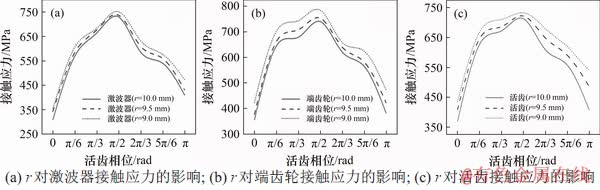
图9 r对各零件接触应力的影响
Fig. 9 Effect of r on contact stress of each part
3.3 沟曲率半径系数对接触应力的影响
图10所示为沟曲率半径系数f对二齿差摆盘式活齿传动中各零件在整个传动过程中的接触应力的影响。
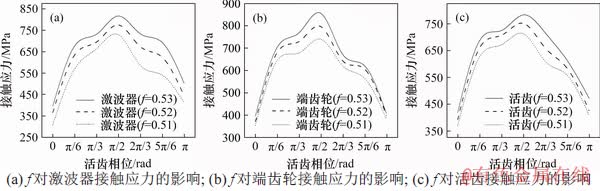
图10 f对各零件接触应力的影响
Fig. 10 Effect of f on contact stress of each part
与活齿半径r相似,沟曲率半径系数f对各零件的接触应力的影响情况也比较简单,图10中各图线之间同样没有出现交叉。与r不同的是,f与各零件在不同相位的接触应力均呈正相关。
分析原因是:沟曲率半径系数f的变化改变了接触点处导槽一侧的主曲率,使之成为影响接触应力的主要因素。
4 二齿差摆盘式活齿传动的接触疲劳分析
查阅相关资料可知[15],轴承钢GCr15经淬火加回火处理后的屈服强度可达1 665~1 815 MPa,远大于前文所得结果。并且,发生塑性变形并不代表结构破坏失效。对于接触面积较小的球体、圆柱等曲面接触,在实际工作中,接触部位一旦受压,即会发生塑性变形,使接触面积增大,接触应力迅速降低,塑性区不会扩大,整个结构仍能正常工作。
在循环接触条件下工作的零件的失效形式通常是接触表面的疲劳破坏。由于接触应力的循环作用,使材料次表面发生反复切向滑移,导致初始疲劳裂纹的产生,并逐步扩展到表面,最后形成片状剥落,即疲劳点蚀。点蚀会降低零件传递载荷的能力,引起振动和噪声。因此,有必要对次表面的应力分布及系统的接触疲劳强度做进一步分析讨论。
关于应力对接触疲劳的影响,通常认为:次表面下材料的塑性变形与最大切应力有关,而疲劳裂纹的发生和扩展则是由交变切应力所导致[16]。
考虑到在二齿差摆盘式活齿传动系统的传动过程中,球形活齿是不断滚动自旋的,在活齿的每个工作过程中其受载最大的区域是不断变化的,在不发生过载压溃的情况下,其疲劳强度显然比危险区域固定不变的激波器和端齿轮的大。因此,后文仅以激波器和端齿轮为分析对象,研究其接触表面以下的各应力分布状态。
4.1 次表面应力分布状态
图11所示为激波器与端齿轮的等效应力的截面图(φ=π/2 rad),截面垂直于激波器转动的切线方向。从图11可以看出:等效应力最大值均出现在接触表面以下;在次表面深度为0.2~0.4 mm的范围,沿着与运动方向相垂直的方向形成了一道狭长的弧形应力集中区域。
等效应力遵循材料力学第四强度理论,该理论认为当物体内某一点的等效应力达到某一定值时,该点即进入塑性状态。从等效应力的分布可以直观地找到各零件易发生破坏的危险区域。
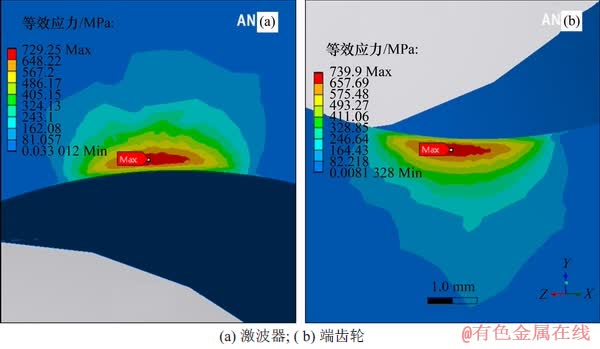
图11 等效应力截面图
Fig. 11 Equivalent stress section
图12所示为激波器与端齿轮的最大切应力的截面图,截面平行于激波器转动的切线方向。从图12可以看出:最大切应力同样分布于接触点下方,分布深度与等效应力基本相同,位于0.2~0.4 mm的范围。
材料力学第三强度理论认为最大切应力是导致材料屈服的主要因素。因此,在最大切应力较大的位置需要特别关注材料可能发生的塑性变形,而次表面的塑性变形导致的材料切向滑移是引发初始疲劳裂纹的重要因素。
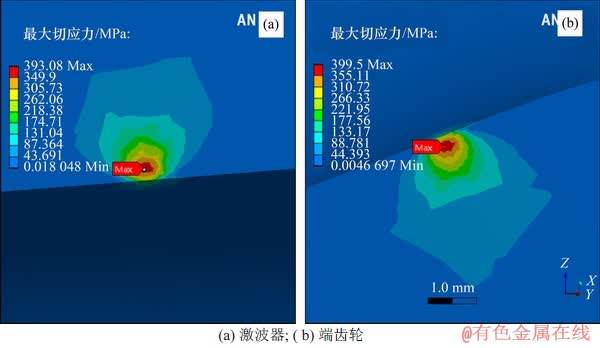
图12 最大切应力截面图
Fig. 12 Maximum shear stress section
不同方向的切应力对接触疲劳均有影响,其中沿滚道周向的切应力影响最大[17-18]。图13所示为激波器与端齿轮在接触点处的切应力截面图,截面平行于激波器转动的切线方向,可见切应力在接触点下方沿运动方向呈正负交替分布。
在二齿差摆盘式活齿传动循环接触的传动过程中,正负交替变化的切应力反复作用于端齿轮和激波器的导槽次表面,最终导致疲劳裂纹的不断扩展直至形成点蚀。
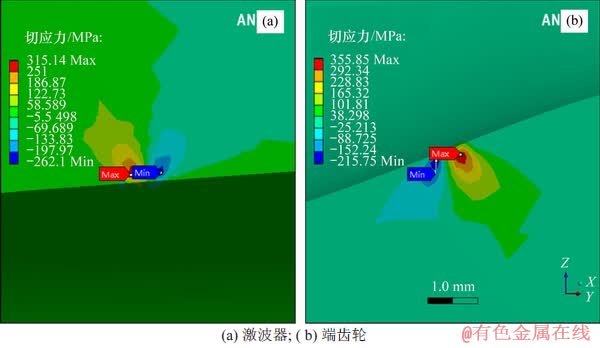
图13 切应力截面图
Fig. 13 Cut stress section
4.2 疲劳寿命分析
在二齿差摆盘式活齿传动中,激波器与端齿轮的接触应力最大值十分接近,在正常工作条件下,两者应当具有相近的疲劳强度。但由于传动比的存在,两零件的工作频率并不相同,这将可能导致工作频率高的零件成为系统中疲劳失效的危险区域。因此,有必要对两零件共同工作时各自的疲劳寿命进行计算,从而对系统疲劳失效的危险区域进行预先判断。
Workbench中的Fatigue模块提供一种快速的疲劳分析方法,该模块对诸如平均应力、载荷条件及疲劳强度的缩减等影响疲劳寿命的因子予以综合考虑,采用线性累积损伤理论进行疲劳寿命的计算。
定义疲劳强度因子为0.8,考虑到零件在工作时的受力状况,定义载荷类型为脉动循环变载荷,进行求解。所得结果为以循环次数为单位的疲劳寿命:端齿轮为6.419 6×1011r,激波器为6.768×1011r。
上述结果为零件的每一处危险区域(即φ=π/2 rad时与活齿的接触点)在当前仿真条件下所能达到的循环次数。由于活齿数为8,端齿轮及激波器每旋转1周,各危险区域均经过8次循环,再考虑到传动比为5,端齿轮每旋转1周,激波器对应旋转5周。因此,若以传动系统的输入轴转数作为疲劳寿命单位,经换算后可得端齿轮为4.012 2×1011r,激波器为8.46×1010r。
可见,换算后的激波器的疲劳寿命比端齿轮的小,说明在实际工作过程中,激波器因为转速较大,更容易发生疲劳破坏而导致系统整体失效,故而可以考虑为激波器选用强度更高的材料,以延长传动系统的使用寿命。又由前面分析可知,接触表面以下深度为0.2~0.4 mm的范围是初始疲劳裂纹产生的危险区域,因此还可以考虑对导槽进行表面强化处理,通过调整工艺参数得到适宜的硬化层深度和硬度,以提高零件的接触疲劳强度。
5 结论
1) 依据二齿差活齿传动的对称性原理对系统模型进行了简化,通过ANSYS Workbench运用有限元分析方法求解了各零件在接触点附近的等效应力。各零件的应力均集中在接触点附近的微小区域内,分布状态符合预期,属于典型的接触问题,同时验证了差异化网格划分的合理性。
2) 对于二齿差摆盘式活齿传动,在活齿的一个完整的动态工作过程之中,各零件的接触应力整体呈现先增大后减小的趋势,并在活齿相位φ=π/2 rad时达到最大,其中活齿架的应力始终较小。在以上分析与计算过程中总结出一套针对活齿传动的快速有效的有限元分析方法,具体可概括为:局部的网格细化、模型的对称性简化、利用组件功能一求多解。
3) 各参数对接触应力的影响情况不同,其中活齿振幅的影响较为复杂需要分段讨论,而活齿半径及沟曲率半径系数的影响则相对简单。若仅考虑各零件的接触应力最大值,则三者的影响较为明确,即振幅增大、活齿半径增大、沟曲率半径系数减小均会导致接触应力最大值的减小,反之亦然。
4) 在静强度校核的基础上,应用接触力学的各经典理论,研究了接触点次表面不同类型应力的分布状态,并对系统进行了疲劳分析,计算了系统的接触疲劳寿命并确定了系统疲劳失效的危险区域。系统在10 kN·mm的负载下不会发生静强度失效,其疲劳寿命若以输入轴转数计则为8.46×1010 r,其中激波器由于转速较高,将最先发生失效,而接触表面以下深度为0.2~0.4 mm是初始疲劳裂纹产生的危险区域。
参考文献:
[1] 曲继方. 活齿传动理论[M]. 北京: 机械工业出版社, 1993: 77-102.
QU Jifang. Theory of movable tooth transmission [M]. Beijing: Mechanical Industry Press, 1993: 77-102.
[2] 龚曙光. ANSYS工程应用实例解析[M]. 北京: 机械工业出版社, 2003: 63-79.
GONG Shuguang. Analysis of ANSYS engineering application example[M]. Beijing: Mechanical Industry Press, 2003: 63-79.
[3] YAYLACI M, ONER E, BIRINCI A. Comparison between analytical and ANSYS calculations for a receding contact problem[J]. Journal of Engineering Mechanics, 2014, 140(9): 04014070.
[4] HAJDU S . Investigation of stress state and contact pressures in contact area of journal bearing by numerical simulation[J]. Applied Mechanics and Materials, 2014, 474: 200-205.
[5] 梁尚明, 张均富, 徐礼钜. 摆动活齿传动系统振动的动力学模型[J]. 振动工程学报, 2003, 16(3): 285-289.
LIANG Shangming, ZHANG Junfu, XU Lizhen. Dynamic model of vibration of swing movable transmission system[J]. Journal of Vibration Engineering, 2003, 16(3): 285-289.
[6] GULER M A, KUCUKSUCU A, YILMAZ K B, et al. On the analytical and finite element solution of plane contact problem of a rigid cylindrical punch sliding over a functionally graded orthotropic medium[J]. International Journal of Mechanical Sciences, 2017, 120: 12-29.
[7] 王素, 白鑫, 陈仕贤, 等. 离散齿谐波传动啮合力及接触应力分析[J]. 重庆大学学报, 2013, 36(1): 35-42.
WANG Su, BAI Xin, CHEN Shixian, et al. Analysis of meshing force and contact stress of discrete tooth harmonic transmission[J]. Journal of Chongqing University, 2013, 36(1): 35-42.
[8] 李瑰贤, 孙瑜, 李笑. 圆柱正弦活齿传动受力分析研究[J]. 哈尔滨工业大学学报, 2003, 35(11): 1381-1383.
LI Guixian, SUN Yu, LI Xiao. Research on force analysis of cylindrical sinusoidal teeth transmission[J]. Journal of Harbin Institute of Technology, 2003, 35(11): 1381-1383.
[9] TOUMI M, CHOLLET H, YIN H. Finite element analysis of the frictional wheel-rail rolling contact using explicit and implicit methods[J]. Wear, 2016, 366/367: 157-166.
[10] 梁尚明, 罗伟, 徐俊光. 摆动活齿减速器系统有限元模态分析[J]. 四川大学学报(工程科学版), 2004, 36(2): 77-80.
LIANG Shangming, LUO Wei, XU Junguang. Finite element modal analysis of swing movable gear reducer system[J]. Journal of Sichuan University (Engineering Science Edition), 2004, 36(2): 77-80.
[11] 赵纯可, 梁尚明, 张杰. 二齿差摆杆活齿传动的齿形分析与仿真[J]. 四川大学学报(工程科学版), 2015, 47(S1): 151-157.
ZHAO Chunke, LIANG Shangming, ZHANG Jie. Analysis and simulation of tooth profile of two-tooth difference pendulum movable teeth transmission[J]. Journal of Sichuan University (Engineering Science Edition), 2015, 47(S1): 151-157.
[12] 李剑锋, 何爱颖, 董新蕊. 凸轮激波滚动活齿传动的几何设计[J]. 机械工程学报, 2011, 47(1): 24-30.
LI Jianfeng, HE Aiying, DONG Xinrui. Geometric design of cam shock rolling movable teeth drive[J]. Journal of Mechanical Engineering, 2011, 47(1): 24-30.
[13] 韩晓娟, 杨茂坤. 二齿差摆线类活齿传动齿形设计及活齿动态响应分析[J]. 机械传动, 2015(9): 70-73.
HAN Xiaojuan, YANG Maokun. Tooth shape design and dynamic response analysis of movable teeth of two-tooth differential cycloidal gears[J]. Mechanical Transmission, 2015(9): 70-73.
[14] 张学东. 空间曲线的曲率计算方法[J]. 塔里木农垦大学学报, 2002, 14(2): 37.
ZHANG Xuedong. Curvature calculation method for spatial curves[J]. Journal of Tarim Agricultural University, 2002, 14(2): 37.
[15] HARRIS T A, KOTZALAS M N. 轴承技术的基本概念[M]罗继伟, 译. 北京: 机械工业出版社, 2010: 114-116.
HARRIS T A, KOTZALAS M N. Basic concepts of bearing technology[M]. LUO Jiwei, trans. Beijing: Mechanical Industry Press, 2010: 114-116.
[16] SOHOULI A R, GOUDARZI A M, ALASHTI R A. Finite element analysis of elastic-plastic contact mechanic considering the effect of contact geometry and material properties[J]. Journal of Surface Engineered Materials and Advanced Technology, 2011, 1(3): 125-129.
[17] COOLEY C G, LIU Chunguang, DAI Xiang, et al. Gear tooth mesh stiffness: a comparison of calculation approaches[J]. Mechanism and Machine Theory, 2016, 105: 540-553.
[18] TOUMI M, CHOLLET H, YIN H. Finite element analysis of the frictional wheel-rail rolling contact using explicit and implicit methods[J]. Wear, 2016, 366/367: 157-166.
(编辑 杨幼平)
收稿日期:2019-03-22;修回日期:2019-06-10
基金项目(Foundation item):国家自然科学基金资助项目(51705347) (Project(51705347) supported by the National Natural Science Foundation of China)
通信作者:梁尚明,博士,教授,从事先进传动技术及现代设计方法等研究;E-mail: 15198161798@163.com