Modeling of strain hardening and dynamic recrystallization of ZK60 magnesium alloy during hot deformation
来源期刊:中国有色金属学报(英文版)2012年第2期
论文作者:潘清林 李文斌 刘晓艳 张志野 陈琴 何运斌
文章页码:246 - 254
关键词:镁合金;流变应力;应变强化;动态再结晶;热变形
Key words:magnesium alloys; flow stress; strain hardening; dynamic recrystallization; hot deformation
摘 要:
研究ZK60合金的高温流变应力行为。分别采用Kocks-Mecking模型和Avrami方程对合金的应变强化和动态再结晶过程进行模拟,在此基础上,构建一个考虑合金动态再结晶软化的流变应力方程并对流变应力进行预测。结果表明:预测曲线与实验结果具有很高的相关系数,所构建的流变应力方程能准确地描述热变形过程中合金的流变应力行为。微观组织观察表明在变形初期合金组织主要为动态回复组织,随着应变增加,逐渐转变为再结晶组织。
Abstract:
The flow stress behavior of ZK60 alloy at elevated temperature was investigated. The strain hardening and dynamic recrystallization of the alloy were modeled by Kocks-Meching model and Avrami equation, respectively. A new constitutive equation during hot deformation was constructed to predict the flow stress considering the dynamic recrystallization. The results show that the flow stress curves predicted by the proposed equation have high correlation coefficients with the experimental data, which confirms that the developed model is accurate and effective to establish the flow stress equation of ZK60 magnesium alloy during hot deformation. Microstructure observation shows that dynamic recovery occurs in the initial stage of hot deformation. However, the microstructure turns to recrystallization structure as the strain increases.

![]()

Trans. Nonferrous Met. Soc. China 22(2012) 246-254
HE Yun-bin, PAN Qing-lin, CHEN Qin, ZHANG Zhi-ye, LIU Xiao-yan, LI Wen-bin
School of Materials Science and Engineering, Central South University, Changsha 410083, China
Received 1 March 2011; accepted 25 June 2011
Abstract: The flow stress behavior of ZK60 alloy at elevated temperature was investigated. The strain hardening and dynamic recrystallization of the alloy were modeled by Kocks-Meching model and Avrami equation, respectively. A new constitutive equation during hot deformation was constructed to predict the flow stress considering the dynamic recrystallization. The results show that the flow stress curves predicted by the proposed equation have high correlation coefficients with the experimental data, which confirms that the developed model is accurate and effective to establish the flow stress equation of ZK60 magnesium alloy during hot deformation. Microstructure observation shows that dynamic recovery occurs in the initial stage of hot deformation. However, the microstructure turns to recrystallization structure as the strain increases.
Key words: magnesium alloys; flow stress; strain hardening; dynamic recrystallization; hot deformation
1 Introduction
Flow stress is a basic parameter for characterizing the mechanical properties of materials during hot deformation. It is determined by the deformation temperature, strain rate and strain. It is also a comprehensive reflection of microstructure evolution [1]. Therefore, it is not only important in determining the processing parameters [2] but also in investigating the deformation mechanism during hot deformation [3].
The modeling of the flow stress for hot deformation has been extensively investigated in the past few years [4-6]. Hollomon [7] developed the classic engineering description at small plastic strain. Voce [8] proposed a simple but formally similar equation. Chinh et al [9, 10] used the Voce equation to describe the hardening in aluminum processed by equal channel angular pressing over a wide range of strain. McQueen and Ryan [11] also developed another empirical and phenomenological model to represent the stress—strain curves for high strain and strain rate hot working. However, the models aforementioned are basically engineering fit equations without physical significance and they are weak in revealing the relationship between microstructure evolution and mechanical properties. Therefore, Mecking and Kocks [12] and Estrin and Mecking [13] proposed that the stress—strain relationship can be described by a structural parameter model (i.e. dislocation density). However, all these models are mainly concerned about the strain hardening behavior during the hot deformation process, while little attention is paid to the softening behavior at high strain. Establishing flow stress equation for hot deformation requires quantitative understanding of the dynamic softening during deformation. Two basic major dynamics softening processes are dynamic recovery and dynamic recrystallization, both the processes have a profound influence on the hot deformation behavior of metals and alloys and also on their final microstructure and properties. Zhao et al [14] and Lin et al [15] developed the dislocation-based model to describe the relationship between viscoplastic flow and microstructure evolution of steel. However, no such constitutive equations are available to model the effects of dynamic recrystallization on the microstructure evolution and interactive relationships of dynamic recrystallization, microstructure evolution and viscoplastic deformation of magnesium alloys.
In the case of magnesium and its alloys, owing to the relatively low stacking fault energy and lack of independence slip systems, dynamic recrystallization plays an important role during hot deformation. Unlike most aluminum alloys and steels, for magnesium alloys with dynamic recrystallization, the flow stress initially increases with strain due to work hardening, and the flow stress begins to decrease after it reaches a certain peak value as dynamic recrystallization takes place upon critical strain. Cerri et al [16] investigated the flow behavior of AZ91 magnesium alloy and found that when the equilibrium is reached between softening due to dynamic recrystallization and work hardening, the curves drop to a steady-state region.
Mirzadeh and NAJAFIZADEH [17] employed the Avrami equation to describe the static recrystallization kinetics. It is now of interest to examine the extent of dynamic recrystallization, to which the Avrami equation is applied. JONAS et al [18] successfully extended the modified Avrami equation to analyze the dynamic recrystallization softening process during hot deformation.
The aim of the present study is to analyze the strain hardening and softening behavior of ZK60 magnesium alloy and construct a universal flow stress model by combining the Kocks-Meching (KM) model and Avrami equation to describe the flow stress over a wide range of strain.
2 Experimental
The material used was commercial ZK60 magnesium alloy (5.78% Zn and 0.76% Zr, mass fraction). The starting material was a semi-continuous casting ingot with an average grain size of 100 μm. Prior to hot deformation, the ingot was homogenized at 673 K for 12 h. Small cylindrical compression specimens with dimensions of d10 mm×15 mm were machined out from the as-received ingot. Two sets of specimens were subjected to uniaxial compression tests. One set was carried out in the temperature range from 423 to 673 K at intervals of 50 K at a constant strain rate of 0.01 s-1 and the other set was carried out at strain rate ranging from 0.001 to 10 s-1 with intervals of an order of magnitude at a constant temperature of 523 K. All the compression tests were conducted on a Gleeble-1500 thermal simulator up to height reduction of 60%, giving a true strain of about 0.9. The temperature of the specimens was monitored and controlled by a thermocouple welded at the half height of the specimens. Concentric grooves were provided on both contact surfaces of the specimens to ensure effective lubrication during compression. Molybdenum disulphide-graphite paste was used as lubricant. All the specimens were heated at 10 K/s up to the deformation temperatures and held for 3 min until the temperature through the whole sample was homogenous. The load-displacement data were obtained from the compression tests and then convert to true stress—strain curves using standard equations. After compression test, the specimens were water quenched to preserve the final microstructure.
The transmission electron microscopy (TEM) microstructure observations were carried out on a Tecnai G2 20 at 200 kV. The specimens were prepared using ion milling at 4 keV.
3 Constitutive equation
3.1 Flow stress behavior
The true stress—strain curves for ZK60 magnesium alloy at different strain rates and temperatures are shown in Fig.1. The flow stress increases to a maximum and then decreases to a steady state, which shows a typical characteristic of hot working accompanied by dynamic recrystallization (DRX). It is obvious that the flow stress curves can be divided into four different stages, i.e., stage I work-hardening stage, stage II transition stage, stage III softening stage and stage IV steady stage, as shown in Fig. 2. This is a comprehensive reflection of work hardening and thermally activated softening [19]. In the work-hardening stage, dislocations are generated rapidly, which results in fast strain hardening, and the flow stress increases abruptly at initial deformation. In the transition stage, dynamic recovery and dynamic recrystallization start to occur. But work hardening is still the governing mechanism. Therefore, the flow stress keeps increasing but the increasing rate is much slower. In the softening stage, the dislocations are annihilated through the migration of high angle boundaries and the stress starts to decrease gently, which is supposed to be related with DRX. Finally, the stress becomes steady when a new balance between softening and hardening is achieved.
3.2 Modeling of strain hardening
Mecking and Kocks [12] proposed an equation describing the flow stress σ related to the average total dislocation density ρ as:
![]() (1)
(1)
where α is a numerical constant; G is the shear modulus and b is the Burgers vector.
During hot deformation, the evolution of dislocation density ρ with strain ε can be described by KM model as [13]:
dρ/dε=k1ρ1/2-k2ρ (2)
where the first term k1ρ1/2 represents the work hardening, which is associated with athermal storage of moving dislocations; the second term k2ρ is the softening contribution due to dynamic recovery through dislocation annihilation and rearrangement which is dependent on strain rate and temperature.
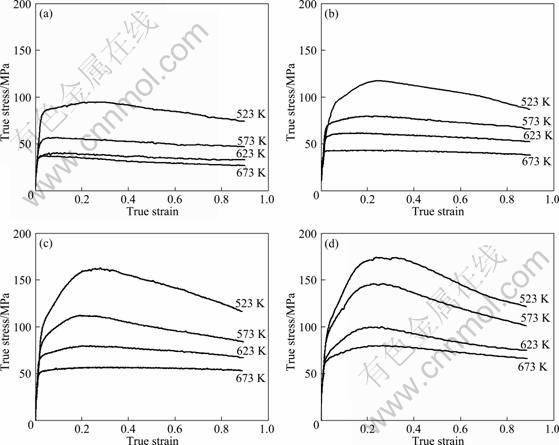
Fig. 1 True stress—strain curves of ZK60 magnesium alloy at different strain rates and temperatures: (a) 0.001 s-1; (b) 0.01 s-1; (c) 0.1 s-1; (d) 1 s-1
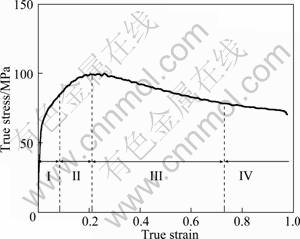
Fig. 2 Typical stress—strain curve of ZK60 alloy at elevated temperature
By employing the initial condition ρ=ρ0, when ε=0, Eq. (2) can be easily solved as:
![]() (3)
(3)
Combing Eqs. (1) and (3), as shown in the Appendix, the flow stress can be given as:
![]() (4)
(4)
where σsat is the saturated stress at steady state corresponding to dρ/dε=0, and it is deduced as:
![]() (5)
(5)
3.3 Modeling of softening by dynamic recrystallization
Strain softening of metals during plastic deformation at high temperature is ascribed to dynamic recovery and dynamic recrystallization. In KM model, only dynamic recovery is included in calculating the flow stress. However, dynamic recrystallization is also a predominant contributor to the decrease of flow stress at high strain. The schematic curves are shown in Fig. 3. Here the uppermost curve is referred to the dynamic recovery acting only, namely, in the absence of dynamic recrystallization. It can be employed to describe the working hardening behavior of the unrecrystallized regions. This can be derived from the work hardening behavior prior to εc. Here εc is the critical strain where dynamic recrystallization starts to occur. After that, DRX is responsible for the softening of the flow stress. At saturation, the value of the asymptotic stress is given by σsat. On continued straining, σsat represents the dislocation density in the most work hardened grains and therefore the driving force for the continuation of dynamic recrystallization.

Fig. 3 Stress—strain curve of ZK60 alloy during hot deformation showing typical softening behavior at high strain
The dynamic recrystallization fraction is defined as:
![]() (6)
(6)
where σsat is the predicted flow stress according to the KM model; σss is the experimental data of flow stress at steady state.
The dynamic recrystallization kinetics can be also described using an Avrami type equation. Gronostajski [20] has sucessfully employed the modified Avrami equation to discribe the dynamic recrystallization during hot deformation. A similar approach proposed by Oudin et al [21] is employed here.
![]() (7)
(7)
where r and q are constants depending on chemical composition and hot deformation conditions; εp is close to the peak strain depending on strain rate and deformation temperature, it can be expressed as:
![]() (8)
(8)
where A and n are material constants; Q is the activation energy; R is the gas constant and T is the absolute temperature. The meaning of q is considered to be relevant to the softening kinetics, namely, the strain softening rate increases with increasing q, and r is to determine how fast the stress goes to reach its steady state with balanced strain hardening and softening behavior. Both r and q can be determined by fitting the experimental data.
Incorporating Eqs. (6) and (7), a universal equation of stress and strain can be obtained to characterize the strain hardening and softening at large strains.
![]() (9)
(9)
It also can be written as:
![]() (10)
(10)
4 Verification of constitutive equation
4.1 Strain hardening
Part of the plastic strain section of flow stress curve during hot deformation is fitted and smoothed with an 8-order polynomial. The smoothing process eliminated the irregularities and fluctuations in the experimental curves and the differentiations can be operated subsequently. An example of the experimental curves is given in Fig. 4, together with its fitted curve. To determine the saturated stress σsat in Eq. (4), the plots of strain hardening rate θ=dσ/dε against stress σ are presented in Fig. 5. The saturated stress is determined by extrapolating the θ—σ plot to θ=0 (using only the linear portion of the curve just below σc), as shown in Fig. 5.

Fig. 4 Experimental stress—strain curve determined in hot compression and corresponding fitted curve of plastic strain with 8-order polynomial
Knowing the values of σsat, one further parameter k2 is needed for the construction of DRV from the data. The values of k2 can be determined by plotting 2ln(1-σ/σsat) against strain ε. An example of determination k2 is shown in Fig. 6. It is noted that the slope is derived from the experimental data obtained prior to εc and σc. The deviation of the curve from linearity after σc is mainly due to the softening effect of dynamic recrystallization.
Knowing the values of σsat and k2, the work hardening curve pertaining to the regions that has not yet undergone dynamic recrystallization can be constructed now. The curves for different deformation temperatures are displayed in Fig. 7. It is necessary to note that there is still deviation between the proposed model and the experimental data. The main reason might be ascribed to dynamic recrystallization prior to the peak strain. As demonstrated in Fig. 3, the initial strain εc where the dynamic recrystallization begins is usually lower than the peak strain, which leads to the lower value of experimental data than the KM model.
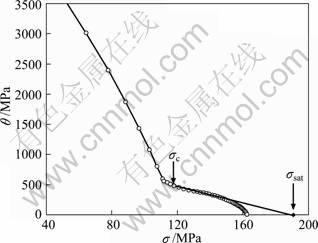
Fig. 5 θ—σ plot derived from fitted curve of Fig. 4 (σsat is defined by intercept with horizontal axis where θ=0)

Fig. 6 Plot of 2ln(1-σ/σsat) vs strain ε employed to determine slope of k2
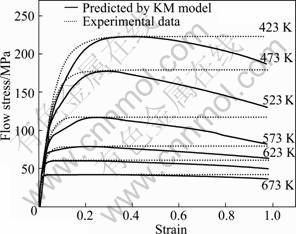
Fig. 7 Comparison of work hardening curves plotted using KM model and experimental data
4.2 Strain softening
In the present approach, since the value of σsat is determined, the recrystallization fraction X of the alloys calculated by Eqs. (6) and (7) can be also rewritten as:
![]() (11)
(11)
Plotting ln[-ln(1-X)] with ln(ε/εp), the values of q and r can be determined by the slope and the intercept of the curve, respectively, as shown in Fig. 8. Therefore, the kinetics of the recrystallization can be described by Eq. (7).

Fig. 8 Plot of ln[-ln(1-X)] vs ln(ε/εp) to determine values of r and q
4.2.1 Effects of temperature and strain rate on kinetics of softening
The effects of temperature and strain rate on the kinetics behavior of ZK60 magnesium are depicted in Figs. 9 and 10. It is evidently seen that at the strain rate of 0.01 s-1, increasing temperature over the range of 423-673 K can accelerate the dynamic recrystallization process. It is easy to understand that the dynamic recrystallization process is thermally activated and the activation energy decreases with the increasing temperature. Due to the low strain rate of 0.01 s-1, all the curves have sufficient time to achieve full recrystallization at the maximum experimental strain of 0.9. It is obvious that the recrystallization process at low temperature has experienced a longer incubation period. With increasing temperature, the incubation period decreases. The dynamic recrystallization is also sensitive to the strain rate. The dynamic recrystallization process is accelerated with decreasing strain rate since lower strain rate provides longer time for dislocation annihilation and rearrangement. Therefore, for a certain strain, the dynamic recrystallization fraction is larger for low strain rate. However, at high strain rate >0.1 s-1, the volume fraction of recrystallization is less than 1 at the final strain and decreases with increasing strain rate. This is because the deformation time is too short for complete recrystallization process at high strain rate. It is expected that a full recrystallized structure might be achieved with further straining. But it is also possible that the samples might suffer cracking before the dynamic recrystallization process is completed at high strain rate.
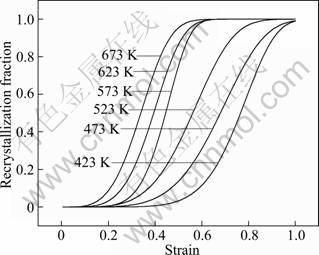
Fig. 9 Avrami plots of recrystallization kinetics at different deformation temperatures at strain rate of 0.01 s-1
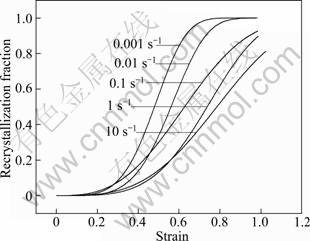
Fig. 10 Avrami plots of recrystallization kinetics at different strain rates at 523 K
4.2.2. Modeling of flow stress
In order to verify the proposed flow stress model, comparisons between the experimental data and predicted results by Eq. (10) are presented in Fig. 11. The correlation coefficients between these two sets of curves at different temperatures and different strain rates are listed in Tables 1 and 2. It is evidently seen that the predicted data are quite consistent with the experimental data, as shown in Figs.11 and 12. All the correlation coefficients are larger than 0.90, indicating a good agreement between the predicted results and experimental data. Therefore, the proposed model is effective and can also well estimate the flow stress for ZK60 magnesium alloy during hot deformation.
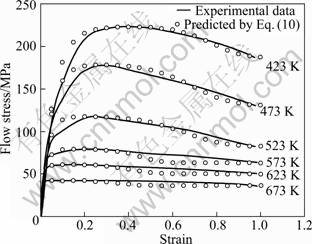
Fig. 11 Flow stress—strain curves estimated by Eq. (10) and experimental data at strain rate of 0.01 s-1 at different temperatures

Fig. 12 Flow stress—strain curves estimated by Eq. (10) and experimental data at 523 K at different strain rates
5 Microstructure evolution during hot deformation
Figure 13 shows the TEM microstructure of ZK60 alloy at different stages of deformation at 523 K. At the initial stage, when the strain is small (ε=0.1), due to the activation of non-basal slip system at elevated temperature, dislocation slip occurs within the grains, as shown in Fig. 13(a). It is also observed that dislocation pile-up at the grain boundaries results in a rapid strain hardening at the initial stage of deformation. Therefore, dislocation generation and pile-up are the dominant mechanisms in the initial stage. As the dislocation density increases, dynamic recovery starts to occur. Dynamic recovery not only slows down the strain hardening effect, but also changes the dislocation configuration. As shown in Fig. 13(b), with increasing strain, the tangled dislocations tend to form cell structure to reduce the entire energy. Those dislocation interfaces in the cell structure are low angle boundary and fragment from great grains into small sub-grains. Further deformation introduces more dislocations into the material and those dislocations are gradually absorbed by the sub-grain boundaries which turn the low angle boundaries into high angle boundaries. As shown in Fig.13(c), after being deformed to strain of 0.6, the microstructure of the ZK60 alloy mainly consists of equiaxial recrystallized grains with high angle boundaries. The results are consistent with the dynamic recrystallization kinetics curves where the recrystallization fraction is near 1 when the strain reaches 0.6 at 523 K. No obvious change is observed when the strain further increases to 0.9. The microstructure is also comprised of small equiaxial recrystallized grains.

Fig. 13 TEM microstructures of ZK60 alloy processed at 523 K and strain rate of 0.01 s-1 at strain of 0.1 (a), 0.3 (b), 0.6 (c) and 0.9 (d)
6 Conclusions
1) The softening effect is mainly due to the dynamic recovery in the initial strain hardening stage and changes to dynamic recrystallization after the stress reaches the peak value. The athermal hardening and dynamic recovery can be evaluated from the strain hardening behavior using KM model.
2) The net softening attributed to DRX is defined as the difference between the dynamic recovery and the experimental data and an Avrami equation is employed to express the softening behavior due to DRX. The new model based on the strain hardening and dynamic recrystallization can accurately predict the flow stress during hot deformation.
3) Dynamic recovery occurs in the initial stage of hot deformation, while the microstructure turns to recrystallization structure as the strain increases.
Appendix
Derivation of work hardening relations
For the present purpose, the evolution of dislocation density ρ with plastic strain ε is given as:
![]() (A1)
(A1)
where ![]() is the athermal work hardening rate and
is the athermal work hardening rate and ![]() specifies the rate of dynamic recovery at given temperature and strain rate. From Eq. (A1), dε can be expressed as:
specifies the rate of dynamic recovery at given temperature and strain rate. From Eq. (A1), dε can be expressed as:
![]()
![]() (A2)
(A2)
Eq. (A2) can also be rewritten as:
![]() (A3)
(A3)
The integration of which is given as:
![]() (A4)
(A4)
where the exponential of the above relation is
![]() (A5)
(A5)
This is equivalent into
![]() (A6)
(A6)
By employing the limiting condition ![]() and ρ=ρ0, the integration constant can be derived as:
and ρ=ρ0, the integration constant can be derived as:
![]() (A7)
(A7)
The combination of Eqs. (A6) and (A7) leads to
![]() (A8)
(A8)
The developed stress is now expressed as![]() , so that
, so that ![]() and
and![]() can be replaced by
can be replaced by ![]() and
and![]() , respectively. Under these conditions, the flow stress can be given by the following relation in terms of the plastic strain as:
, respectively. Under these conditions, the flow stress can be given by the following relation in terms of the plastic strain as:
![]() (A9)
(A9)
When ε tends to infinity, Eq. (A9) can be rewritten as:
![]() (A10)
(A10)
Now ![]() is defined as the dynamic recovery saturation stress, σsat. In this way, Eq. (A9) can be written as:
is defined as the dynamic recovery saturation stress, σsat. In this way, Eq. (A9) can be written as:
![]()
![]() (A11)
(A11)
As ![]() is defined as the flow stress where ε=0, from the experimental data it can be seen that the value of
is defined as the flow stress where ε=0, from the experimental data it can be seen that the value of ![]() is far smaller than σsat. Therefore, an approximation is made that σ0 is negligible compared with σsat. In this case, Eq. (A11) can be approximately expressed as:
is far smaller than σsat. Therefore, an approximation is made that σ0 is negligible compared with σsat. In this case, Eq. (A11) can be approximately expressed as:
![]() (A12)
(A12)
References
[1] Prasad Y, Seshacharyulu T, Medeiros S C, Frazier W G. Microstructural modeling and process control during hot working of commercial Ti-6A1-4V: Response of lamellar and equiaxed starting microstructures [J]. Materials and Manufacturing Processes, 2000, 15(4): 581-604.
[2] Li X, Lu S Q, Fu M W, Wang K L, Dong X J. The optimal determination of forging process parameters for Ti-6.5Al-3.5Mo- 1.5Zr-0.3Si alloy with thick lamellar microstructure in two phase field based on P-map [J]. Journal of Materials Processing Technology, 2010, 210(2): 370-377.
[3] Zong Y Y , Shan D B , Xu M, Lv Y. Flow softening and microstructural evolution of TC11 titanium alloy during hot deformation [J]. Journal of Materials Processing Technology, 2009, 209(4): 1988-1994.
[4] Qin Y J, Pan Q L, He Y B, Li W B, Liu X Y, Fan X. Artificial neural network modeling to evaluate and predict the deformation behavior of ZK60 magnesium alloy during hot compression [J]. Materials and Manufacturing Processes, 2010, 25(7): 539-545.
[5] Qin Y J, Pan Q L, He Y B, Li W B, Liu X Y, Fan X. Modeling of flow stress considering dynamic recrystallization for magnesium alloy ZK60 [J]. Materials and Manufacturing Processes, 2010, 25(7): 527-533.
[6] Lin Y C, Chen M S, Zhang J. Modeling of flow stress of 42CrMo steel under hot compression [J]. Materials Science and Engineering A, 2009, 499(1-2): 88-92.
[7] Hollomon J H. The mechanical equation of state [J]. Trans AIME, 1947, 171: 535-545.
[8] Voce E. The relationship between stress and strain for homogeneous deformation [J]. Journal of Institute Metals, 1948, 74: 537-562.
[9] Chinh N Q, Illy J, Horita Z, Langdon T G. Using the stress—strain relationships to propose regions of low and high temperature plastic deformation in aluminum [J]. Materials Science and Engineering A, 2005, 410-411: 234-238.
[10] Chinh N Q, Szommer P, Csanadi T, Langdon T G. Flow processes at low temperatures in ultrafine-grained aluminum [J]. Materials Science and Engineering A, 2006. 434(1-2): 326-334.
[11] McQueen H J, Ryan N D. Constitutive analysis in hot working [J]. Materials Science and Engineering A, 2002, 322(1-2): 43-63.
[12] Mecking H, Kocks U F. Kinetics of flow and strain-hardening [J]. Acta Metallurgica, 1981, 29(11): 1865-1875.
[13] Estrin Y, Mecking H. A unified phenomenological description of work hardening and creep based on one-parameter models [J]. Acta Metallurgica, 1984, 32(1): 57-70.
[14] Zhao X, Guest R P, Tin S, Cole D, Brooks J W, Peers M. Modelling hot deformation of Inconel 718 using state variables [J]. Materials Science and Technology, 2004, 20: 1414-1421.
[15] Lin J, Liu Y, Farrugia D C J, Zhou M. Development of dislocation-based unified material model for simulation microstructure evolutio in multipass hot rolling [J]. Philosophical Magazine, 2005, 85: 1967-1987.
[16] Cerri E, Leo P, DeMarco P P. Hot compression behavior of the AZ91 magnesium alloy produced by high pressure die casting [J]. Journal of Materials Processing Technology, 2007, 189(1-3): 97-106.
[17] Mirzadeh H, Najafizadeh A. The rate of dynamic recrystallization in 17-4 PH stainless steel [J]. Materials & Design, 2010, 31(10): 4577-4583.
[18] Jonas J J, Quelennec X, Jiang L, Martin ?. The Avrami kinetics of dynamic recrystallization [J]. Acta Materialia, 2009, 57(9): 2748-2756.
[19] Sheng Z Q, Shivpuri R. Modeling flow stress of magnesium alloys at elevated temperature [J]. Materials Science and Engineering A, 2006, 419(1-2): 202-208.
[20] Gronostajski Z. New method of static softening kinetics determination [J]. Journal of Materials Processing Technology, 2004, 157-158: 165-170.
[21] Oudin A, BARNETT M R, HODGSON P D. Grain size effect on the warm deformation behaviour of a Ti-IF steel [J]. Materials Science and Engineering A, 2004, 367(1-2): 282-294.
何运斌, 潘清林, 陈 琴, 张志野, 刘晓艳, 李文斌
中南大学 材料科学与工程学院,长沙 410083
摘 要:研究ZK60合金的高温流变应力行为。分别采用Kocks-Mecking模型和Avrami方程对合金的应变强化和动态再结晶过程进行模拟,在此基础上,构建一个考虑合金动态再结晶软化的流变应力方程并对流变应力进行预测。结果表明:预测曲线与实验结果具有很高的相关系数,所构建的流变应力方程能准确地描述热变形过程中合金的流变应力行为。微观组织观察表明在变形初期合金组织主要为动态回复组织,随着应变增加,逐渐转变为再结晶组织。
关键词:镁合金;流变应力;应变强化;动态再结晶;热变形
(Edited by FANG Jing-hua)
Corresponding author: PAN Qing-lin; Tel: +86-731-88830933; E-mail: pql@csu.edu.cn
DOI: 10.1016/S1003-6326(11)61167-9

