非等模数非等压力角NGW型行星齿轮系静力学均载行为
叶福民1, 2,朱如鹏1,鲍和云1
(1. 南京航空航天大学 机电学院,江苏 南京,210016;
2. 江苏科技大学 机械工程学院,江苏 镇江,212003)
摘要:建立非等模数非等压力角NGW型行星齿轮系的计算模型,针对各齿轮的偏心误差和齿频误差,运用当量啮合误差原理和浮动构件的静力平衡关系,推导出该系统的静力学方程;对方程进行求解并与等模数等压力角系统的均载特性进行比较,同时还讨论太阳轮(或内齿轮)压力角、齿轮误差、啮合刚度与支撑刚度对该系统均载特性的影响。研究结果表明:非等模数非等压力角行星齿轮系有着较好的均载效果,其均载特性不会随着压力角改变而产生大的波动;太阳轮浮动支撑机构对系统的均载特性有很大的改善;选择误差相同的行星齿轮、减小太阳轮和行星轮的支撑刚度均有利于系统均载。
关键词:行星传动;均载;非等模数非等压力角;误差
中图分类号:TH132.4 文献标志码:A 文章编号:1672-7207(2011)07-1960-07
Static load sharing behavior in NGW planetary gear train with unequal modulus and pressure angles
YE Fu-min1, 2, ZHU Ru-peng1, BAO He-yun1
(1. College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics,
Nanjing 210016, China;
2. School of Mechanical Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China)
Abstract: An analytical model for NGW planetary gear train with unequal modulus and pressure angles was presented, and in consideration of the eccentric error and tooth-frequency error of parts, a static equation of the NGW planetary system was developed based on the theory of equivalent mesh error and the principle of static equilibrium. After equation was solved, the load sharing characteristics were compared with the normal gear transmission. Also the load sharing behavior of each planet was analyzed and compared by the sun and the ring pressure angle, the difference of the gear error, the variety of mesh stiffness and support stiffness. The analysis results show that planetary gear train with unequal modulus and pressure angles has better load sharing behavior, which does not change significantly with the different pressure angles, the floating sun gear has improved the load sharing behavior substantially, and the planets fixed with the same production batch and the lower support stiffness of the sun and the planets benefit the load sharing behavior.
Key words: planetary gear train; load sharing; unequal modulus and pressure angles; error
非等模数非等压力角的齿轮传动是指啮合的一对齿轮满足法节相等的啮合条件,但齿轮的模数与压力角并不相等。针对航空产品需要质量小、体积小、承载能力大的行星传动系统的要求,采用内外啮合副的模数与压力角都不相等的设计,可以增加内外啮合副的重合度,综合提高齿轮的承载能力[1]。在行星传动系统中,由多个行星轮形成的功率分流,理论上行星轮可以共同分担载荷。实际上,由于制造与安装偏心误差和齿形误差的影响,载荷在各路传动上的分配很难均匀。最常用的方法是依靠基本构件的浮动,达到载荷分流均衡的目的[2-7]。20世纪90年代,Timothy[3]开始对齿轮传动的均载性能开始进行研究;Kahraman等[4-5]对行星齿轮装置进行了静态力学分析和实验,在该模型中,考虑了齿轮的位置度偏差和齿形误差;陆俊华等[6]用静态力学的方法,对行星轮系中各种均载机构中误差和均载系数的关系进行了研究;袁茹[8]等研究了浮动构件的支承刚度对行星齿轮功率分流动态均衡性的影响;另外,有许多研究者[7-15]从静力学或者动力学角度出发,研究了各种误差、浮动量和构件刚度对行星齿轮或星型齿轮功率分流均衡性的影响。他们研究侧重点各有不同,建立的模型也有较大差别。本文针对非等模数非等压力角行星齿轮系,考虑齿轮的偏心误差和齿频误差、齿轮副的啮合刚度、各构件的支撑刚度以及输入轴、输出轴的扭转刚度等,建立了静力学平衡方程,求解方程并对行星齿轮系统的均载性能进行定量评价,尤其对在齿轮系的模数与压力角是否相等、齿轮压力角发生较大改变等情况下的均载效果进行比较,以便为非等模数非等压力角行星齿轮系的均载机构设计和浮动量确定提供依据。
1 系统的等效力学模型
图1所示为行星传动系统的传动简图,输入扭矩TD经太阳轮Z分流给行星轮Zpi (i=1, 2, …, N;N为行星轮个数),再由内齿轮ZI汇流到行星架C上,传送到输出扭矩TL。该轮系的太阳轮、行星架和行星轮的中心在外力作用下,均有切向、径向及扭转方向的浮动能力,以此来缓冲轮系各构件间冲击力,减小了行星轮所受载荷的不均匀性。
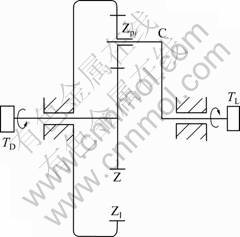
图1 行星传动系统的传动简图
Fig.1 Sketch map of planetary gear train
图2所示为系统静力学均载的计算模型。将行星齿轮系的各构件看作刚体,采用集中质量模型,不计齿轮侧隙与摩擦力的影响,建立以行星架转速ωc旋转的动坐标系,啮合副、回转副及支承处的弹性变形用等效弹簧刚度表示。其中:Ksp为太阳轮和行星轮间的等效啮合刚度;KpI为行星轮和内齿轮间的等效啮合刚度;Ks,Kc和Kp分别为太阳轮,行星架和行星轮支承处的支撑刚度。齿轮副的啮合刚度由GB 3480—97进行计算,支撑刚度由文献[16]中所述方法计算。
该系统共有(8+3N)个自由度,广义坐标为:
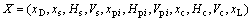 (1)
(1)
式中:xs,Hs和Vs分别为太阳轮沿啮合线方向、中心横向和中心纵向微位移;xpi,Hpi和Vpi分别为第i个行星轮沿啮合线方向、中心径向和中心切向微位移;xc,Hc和Vc分别为行星架的切向、中心横向和中心纵向微位移;xD和xL分别为输入和输出轴的等效微位移;内齿轮固定,故不考虑其各项位移。
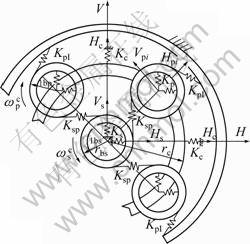
图2 系统的静力学均载计算模型
Fig.2 Static analysis model of planetary gear train
2 系统的啮合角计算
非等模数非等压力角齿轮副,即使在不变位的情况下,它们的分度圆也是不相切的,此时,啮合角不等于任何一个齿轮压力角。可推导出变位时的齿轮副无侧隙啮合方程式:
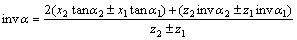 (2)
(2)
式中: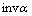 为渐开线函数,
为渐开线函数,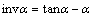 ,
,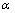 为啮合角;x1和x2为该对齿轮的变位系数;
为啮合角;x1和x2为该对齿轮的变位系数;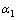 和
和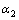 为该对齿轮的压力角;z1和z2为该对齿轮的齿数;“
为该对齿轮的压力角;z1和z2为该对齿轮的齿数;“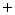 ”用于外啮合副,“–”用于内啮合副。
”用于外啮合副,“–”用于内啮合副。
对于行星齿轮系统,齿轮的变位系数、压力角和齿数分别为xj,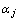 和zj (j对应s, pi, I,分别表示太阳轮、行星轮和内齿轮),由式(2)可以计算出该行星齿轮系的内外啮合的实际啮合角
和zj (j对应s, pi, I,分别表示太阳轮、行星轮和内齿轮),由式(2)可以计算出该行星齿轮系的内外啮合的实际啮合角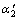 和
和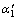 。
。
3 系统的啮合力确定
齿轮副在转动时,内外啮合线上的啮合力由各构件在啮合线上的相对位移和啮合刚度确定。啮合线上相对位移由各构件中心横向(或径向)位移与纵向(或切向)位移的等效位移、各齿轮误差的等效位移、齿轮啮合线上的相对转动位移而构成。
基本构件浮动会引起中心位移的变化,忽略各齿轮中心移动时引起啮合角的微小变化,将各构件的中心位移投影到啮合线上。由啮合的几何关系,太阳轮和行星轮浮动引起的内外啮合线上的侧隙改变量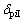 和
和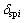 为:
为:
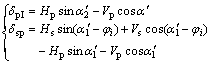 (3)
(3)
式中: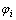 为各行星轮的位置角,
为各行星轮的位置角,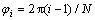 , i=1, 2, …, N。
, i=1, 2, …, N。
各齿轮偏心误差的激励体现在啮合线方向上的位移激励,需将其投影到啮合线方向上。齿轮误差种类很多,为便于研究,本文进行简化处理,认为行星架安装和制造偏心误差均包含在太阳轮和内齿轮的偏心误差中,只需考虑各个齿轮的偏心误差影响即可,其值可用其齿圈的径向跳动公差的一半来表示;齿轮传动的齿频误差可用齿形偏差来表示[15],于是,内外啮合线上产生的当量累计啮合误差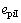 和
和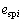 分别为:
分别为:
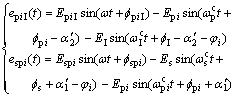 (4)
(4)
式中: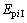 和
和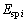 分别为内、外啮合副的齿频误差;
分别为内、外啮合副的齿频误差;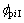 和
和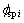 为初相位;
为初相位;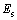 ,
,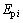 和
和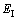 分别为各齿轮的偏心误差;
分别为各齿轮的偏心误差;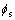 ,
,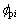 和
和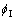 为初相位;
为初相位;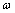 为行星轮系的啮合齿频;
为行星轮系的啮合齿频;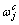 为各构件相对于行星架的转速(j为s, pi, I)。t为时间。
为各构件相对于行星架的转速(j为s, pi, I)。t为时间。
行星传动中由转动位移引起的齿轮副内外啮合线方向的相对位移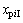 和
和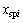 分别为:
分别为:
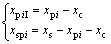 (5)
(5)
再由式(3)~(5)得内外啮合线上的啮合力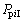 和
和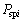 为:
为:
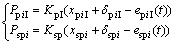 (6)
(6)
其中:i=1, 2, …, N。
4 均载的力学方程与求解
选择合适的坐标系,建立系统的静力平衡方程组:
 (7)
(7)
式中:KD和KL分别为输入端与太阳轮之间和输出端与行星架之间轴的扭转刚度;rbs和rbc分别为太阳轮的基圆半径和行星架的等效基圆半径;FD和FL分别为输入转矩和负载转矩的等效力,FD=TD/rbs,FL=TL/rbc。
求解方程组(7)得到广义坐标X的值,代入式(3)~(6)得内外齿轮副的啮合力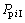 和
和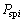 ,再由式(8)得到第i(i=1, 2, …, N)个行星轮的均载系数
,再由式(8)得到第i(i=1, 2, …, N)个行星轮的均载系数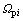 为:
为:
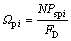 (8)
(8)
定义行星轮均载系数的最大值为系统的均载系数,即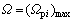 。
。
5 参数影响分析
某行星齿轮减速器的功率为250 kW,输入轴转速为12 000 r/min,行星轮个数为3,采用非等模数非等压力角结构,系统主要参数如表1所示。
表1 系统的主要参数
Table 1 Primary data of planetary gear train
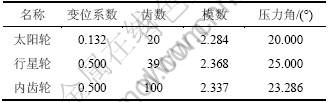
此时的分度圆齿宽系数为0.12,计算出内外啮合刚度KpI和Ksp分别为1.718×108 和4.026×108 N/m;太阳轮和行星轮的支承刚度Ks和Kp分别为7.887×107和4.095×107 N/m;输入轴和输出轴的扭转刚度KD和KL分别为5.26×105和7.46×105 N?m/rad;行星架支承刚度Kc为1.119×108 N/m。各齿轮的精度等级均为5级,由齿轮标准查得相应误差并计算,结果如表2所示。误差相位随机产生。经计算得各行星轮的均载曲线如图3(a)所示,系统的均载系数为1.022 1。
表2 偏心误差与齿频误差
Table 2 Values of eccentric error and tooth-frequency error μm

5.1 与等模数等压力角均载的比较
承载相同扭矩条件下,采用等模数等压力角的原设计,太阳轮、行星轮和内齿轮的齿数分别为20,40和100,模数为2.4,压力角为20°,齿宽系数与前面的相同,重新计算啮合刚度、支撑刚度和扭转刚度等。齿轮精度及各构件误差与前面的相同,计算得各行星轮的均载曲线如图3(b)所示,系统的均载系数为1.024 5。这是由于齿数、模数和压力角等的改变,各种位移在啮合线上的分量产生了变化,内外啮合线上的啮合力与均载系数可能随之发生改变。这里,后者比前者均载系数有所增大,故采用非等模数非等压力角的新型设计,在满足承载能力且系统体积最小时,均载效果有所改善。
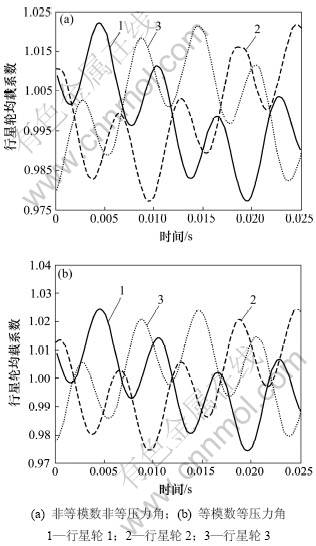
图3 各误差共同作用下的均载系数
Fig.3 Coefficient of load sharing under errors
5.2 分度圆压力角对均载的影响
研究非等模数非等压力角行星齿轮系中压力角对均载系数的影响。为便于比较,设计承载相同扭矩,保持齿宽系数相同,同时各齿轮的齿数不变。(1) 外啮合相等内啮合不等,即太阳轮压力角与行星轮相同,均为20°,内齿轮压力角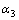 分别在21°~25°之间变化,如表3所示;(2) 外啮合不等内啮合相等,即行星轮压力角与内齿轮相同,均为20°,太阳轮压力角
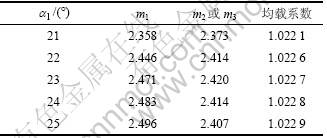
分别在21°~25°之间变化,如表3所示;(2) 外啮合不等内啮合相等,即行星轮压力角与内齿轮相同,均为20°,太阳轮压力角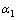 分别在21°~25°之间变化,如表4所示。
分别在21°~25°之间变化,如表4所示。
压力角变化时,模数也随之变化,均载系数如表3和表4所示。由此可见:采用非等模数非等压力角的设计,即使压力角变化幅度大(文中验证的压力角范围为21°~25°,对于满足承载能力和啮合条件的更大压力角范围,文中未列出),均载系数的变化较小,因此该设计在显著减小系统体积的同时,均载效果不会因为压力角的改变而变坏。
表3 不同内齿轮压力角下的均载系数
Table 3 Coefficient of load sharing under different pressure angles of ring gear
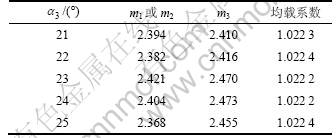
表4 不同太阳轮压力角下的均载系数
Table 4 Coefficient of load sharing under different pressure angles of sun gear
5.3 齿轮偏心误差对均载的影响
研究各构件误差对均载系数的影响,为了便于比较,改变被研究构件误差为6 ?m,同时保持表1中其他误差不变,图4(a)~(c)所示为各偏心误差作用时各行星轮的均载曲线。从图4可见:太阳轮的偏心误差对均载影响最大,内齿轮次之,行星轮最小。此时系统的均载系数分别为1.032 6,1.030 6和1.025 6。由于太阳轮质量小,体积也小,太阳轮浮动较内齿轮浮动方便,应用也更为广泛,必要时可选择内齿轮浮动的机构[2]。
研究各行星轮偏心误差或齿形误差不同时系统均载系数的变化。为与图4(c)比较,改变行星轮偏心误差分别为6,3和3 ?m,均载系数为1.031 8(齿频误差作用时没有列图),如图4(d)所示。因此,在系统进行装配时,应尽可能保证行星轮误差大致相同,以有利于传动系统的均载效果。
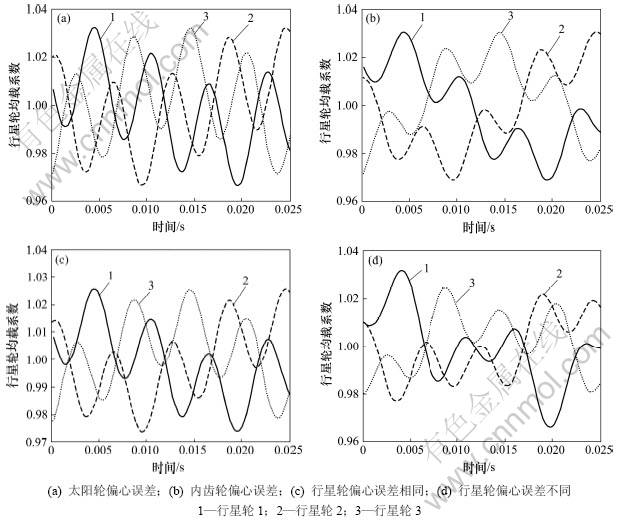
图4 不同单个误差的均载系数
Fig.4 Coefficient of load sharing under different eccentric errors
5.4 刚度对均载的影响
由于太阳轮、行星轮具有较大的浮动量,均载效果较好,内外啮合的啮合刚度变化对均载效果影响不大。而随着太阳轮和行星轮支撑刚度增大,系统均载效果逐渐变差,如表5和表6所示。文献[12]通过齿轮的浮动量考察了太阳轮支撑刚度与均载的关系,其结果与本研究结果一致。因此,在布置太阳轮和行星轮时,应尽量采用柔性布置,比如太阳轮与输入轴间可以增加双齿联轴器等[2]。行星架支撑刚度和输入和输出轴的扭转刚度影响输入和输出端的动力藕合,而对均载效果影响不大。
表5 太阳轮支撑刚度与均载系数
Table 5 Coefficient of load sharing and sun support stiffness

表6 行星轮支撑刚度与均载系数
Table 6 Coefficient of load sharing and planets support stiffness

6 结论
(1) 建立了非等模数非等压力角NGW型行星齿轮系的计算模型和静力学方程;对方程进行求解并与等模数等压力角齿轮系的均载效果进行了比较;讨论了压力角、齿轮误差、啮合刚度与支撑刚度对该系统均载特性的影响。
(2) 非等模数非等压力角行星齿轮系的设计与等模数等压力角齿轮系相比,在质量减小、承载能力提高的同时,均载效果还能有所改善,它为该齿轮系在航空产品上的应用提供了理论支持。
(3) 非等模数非等压力角行星齿轮系的设计时,啮合齿轮压力角可能不相等,且有较大的变化幅度,它的改变对于均载影响不大,均载特性不会随着压力角改变而产生较大的波动。
(4) 太阳轮和内齿轮的浮动对系统的均载性能影响较大;减小太阳轮和行星轮支撑刚度均有利于系统的均载。
(5) 传动系统进行装配时,选择相同误差的行星齿轮,其对系统的均载效果明显,在实际生产中,可以选择同一批次的行星齿轮,以保证误差的一致性。
参考文献:
[1] Seiso S. 变位齿轮[M]. 上海: 上海科学技术出版社, 1984: 244-254.
Seiso S. Proile shifted gear[M]. Shanghai: Shanghai Science and Technology Press, 1984: 244-254.
[2] 饶振纲. 行星齿轮传动设计[M]. 北京: 化学工业出版社, 2003: 181-190.
RAO Zhen-gang. Design of planet gear train[M]. Beijing: Chemical Industry Press, 2003: 181-190.
[3] Timothy L K. A method to analyze and optimize the load sharing of split path transmissions[R]. NASA Technical Memorandum, 1996: 1-18.
[4] Kahraman A. Static load sharing characteristics of transmission planetary gear sets: Model and experiment[J]. Society of Automotive Engineers, 1999(1): 1954-1963.
[5] Kahraman A. Load sharing characteristics of planetary transmissions[J]. Mechanism and Machine Theory, 1994, 29(8): l151-1165.
[6] 陆俊华, 李斌, 朱如鹏. 行星齿轮传动静力学均载分析[J]. 机械科学与技术, 2005, 24(6): 702-704.
LU Jun-hua, LI Bin, ZHU Ru-peng. Analysis of static load sharing in planetary gearing[J]. Mechanical Science and Technology, 2005, 24(6): 702-704.
[7] 袁茹, 王三民, 沈允文. 行星齿轮传动的功率分流动态均衡优化设计[J]. 航空动力学报, 2000, 15(4): 410-412.
YUAN Ru, WANG San-min, SHEN Yun-wen. Dynamic optimum design of power shared out equally among the planetary gears[J]. Journal of Aerospace Power, 2000, 15(4): 4l0-412.
[8] 陈纯. 行星齿轮传动均载构件移量的计算[J]. 机械设计与制造, 2001, 6(3): 52-53.
CHEN Chun. Calculation on the offset of floating component in planetary transmission[J]. Machinery Design & Manufacture, 2001, 6(3): 52-53.
[9] 袁擎宇, 朱如鹏, 朱自冰, 等. 两级星型齿轮传动静力学均载分析[J]. 机械科学与技术, 2004, 23(7): 789-792.
YUAN Qing-yu, ZHU Ru-peng, ZHU Zi-bing, et al. Analysis of static load sharing in a 2-stage star gear system[J]. Mechanical Science and Technology, 2004, 23(7): 789-792.
[10] 袁擎宇. 星型齿轮传动系统均载分析方法的研究[D]. 南京: 南京航空航天大学机电学院, 2004: 6-23.
YUAN Qing-yu. The methodology of analyzing load sharing characteristics of split path star type gear train[D]. Nanjing: Nanjing University of Aeronautics and Astronautics. College of Mechanical and Electrical Engineering, 2004: 6-23.
[11] 鲍和云, 朱如鹏. 两级星型齿轮传动静力学系统基本浮动构件浮动量分析[J]. 中南大学学报: 自然科学版, 2006, 37(3): 553-557.
BAO He-yun, ZHU Ru-peng. Floating displacement static analysis of basic floating part of 2-stage star gear train[J]. Journal of Central South University: Science and Technology, 2006, 37(3): 553-557.
[12] 陆俊华, 朱如鹏, 靳广虎. 基于分流均衡要求的行星传动基本构件浮动量分析[J]. 中南大学学报: 自然科学版, 2008, 39(1): 143-148.
LU Jun-hua, ZHU Ru-peng, JIN Guang-hu. Basic components’ offset analysis of planetary gearing in need of loading sharing[J]. Journal of Central South University: Science and Technology, 2008, 39(1): 143-148.
[13] 陆俊华, 朱如鹏, 靳广虎. 行星传动动态均载特性分析[J]. 机械工程学报, 2009, 45(5): 85-90.
LU Jun-hua, ZHU Ru-peng, JIN Guang-hu. Analysis of dynamic load sharing behavior in planetary gearing[J]. Journal of Mechanical Engineering, 2009, 45(5): 85-90.
[14] 方宗德, 沈允文, 黄镇东. 2K-H行星减速器的动态特性[J]. 西北工业大学学报, 1990, 10(4): 361-371.
FANG Zong-de, SHEN Yun-wen, HUANG Zhen-dong. Dynamic characteristics of 2K-H planetary gearing[J]. Journal of Northwestern Polytechnical University, 1990, 10(4): 361-371.
[15] 孙智民. 功率分流齿轮传动系统非线性动力学研究[D]. 西安: 西北工业大学机械系, 2001: 119-137.
SUN Zhi-min. Research on nonlinear dynamic of split-power gear system[D]. Xi’an: Northwestern Polytechnical University. Department of Mechanical Engineering, 2001: 119-137.
[16] 刘鸿文. 材料力学[M]. 北京: 高等教育出版社, 2004: 176-197.
LIU Hong-wen. Mechanics of material[M]. Beijing: Higher Education Press, 2004: 176-197.
(编辑 陈爱华)
收稿日期:2010-05-10;修回日期:2010-08-21
基金项目:国家自然科学基金资助项目(50775108);航空科技创新基金资助项目(08B52004)
通信作者:朱如鹏(1959-),男,江苏建湖人,教授,博士生导师,从事机械传动、结构强度、机械CAD及自动化研究;电话:025-84892500;E-mail: yfmcn@hotmail.com