J. Cent. South Univ. Technol. (2007)01-0042-05

DOI: 10.1007/s11771-007-0009-0               

Numerical simulation on electrolyte flow field in 156 kA drained aluminum reduction cells

ZHOU Nai-jun(周乃君)¹, XIA xiao-xia(夏小霞)², WANG Fu-qiang(王富强)¹

(1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;

Key words: drained aluminum reduction cells; electrolyte; two-phase flow; numerical simulation

The movement of electrolyte has great important influence on the mass transfer process (such as the dissolution and diffusion of alumina, the re-oxidation reaction of aluminum) and heat transfer process (such as the heat transfer between electrolyte and freeze) in aluminum reduction cells^[1]. WAHNSIEDLER^[2] used PHOENICS to compute electrolyte flow field under electromagnetic force in 155 kA aluminum reduction cells which entered current from big side. It was found that the flow field formed in four eddies which arranged along the long axis, and each big side had two, and the highest velocity was 16.9 cm/s. Based on FLUENT software, PURDIE et al^[3] used three dimension mathematic model to compute the electrolyte flow field under action of anode gas and concluded that the anode gas could be the main driving force of electrolyte movement. GAO et al^[4] used two dimension mathematic model to compute the electrolyte flow field under action of anode gas, and selected homogeneous flow model and found that electrolyte mainly moved around anode, and the electrolyte velocity was highest on anode surface, but least around cathode. It was advantageous for releasing anode gas and the movement of underlayer melted aluminum. Based on FLUENT, BILEK et al^[5] used three dimension mathematic model to compute electrolyte flow field in aluminum cells which entered current from double ends, and found that the movement of electrolyte caused by anode gas was the main factor of heat transfer and mass transfer processes in aluminum reduction cells.

The research on bath flow becomes more and more important for the development of the drained cells. The problem of anode gas releasing would be very important because there is no aluminum liquid layer in drained cells and the lower anode-cathode- distance (ACD). If the anode gas in electrolyte could not be let out easily but gathered between the poles, the voltage of cell and the energy consumption would go up because of the diselectricity of gas; at the same time, it would induce the frequent anode effect, even the local turnoff. In order to avoid the deposition in the base of cells, the appended alumina must be distributed evenly, however, the dissolution and diffusion of alumina in electrolyte depends on the movement of electrolyte completely. So, the electrolyte movement in drained cells is the key factor for the exploitation of drained cells.

The movement of electrolyte in aluminum reduction cells is relatively complex, so the following hypothesis has been brought forward to simplify the calculation when the flow field of electrolyte is simulated:

1) Neglect the influence of alumina particles, and treat the flow of electrolyte as gas-fluid two-phase flow.

2) Regard the flow of electrolyte as steady state and incompressible flow.

3) Regard the electrolyte as isothermal flow without heat transfer.

Taking multi-fluid model of methods of Euler’s－Euler’s, and treating the electrolyte as turbulence and the anode gas as laminar flow, and taking standard k-ε turbulent model, then the Reynolds equation group can be written as follows^[6]:

           (1)

where  φ is general variable, including velocity, k, ε and other scalars; Γ_φα is turbulent diffusion coefficient; S_φα is source; C_αβ is the coefficient of transmission between phases, C_αα=0, C_αβ=C_βα. In Eqn.(1) from left to right, there are convection term, diffusion term, source and transmission between two-phase, so the sum of transmission in all the phases equals 0.

The relevant field of electromagnetic force in calculation is gotten from the method which is similar to Refs.[7-8].

3 Simulation research on electrolyte flow field

3.1 Research object and mesh system

The research object of this study is a drained cell which is reconstructed from a 156 kA prebake anode aluminum reduction cell entering current from both ends^[9-10]. The cathode surface of the drained cells above is coated with composite material TiB₂ of 3-5 mm in thickness. In order to fit for present center point feeding system, the surface of carbon piece inclines from middle to both sides. The working out slope angle of cathode is 2.5?-10?, ACD is 2.5-3.5 cm, and grooves both on middle and surrounding. Moreover, the landscape connection groove between middle and surrounding aluminum collection groove is set to gather the molten aluminum liquid better. The central aluminum collection groove and landscape connection groove are shaped in rectangle cross section, and the surrounding aluminum collection groove is shaped in trapezoid cross section combining with artificial leg. In order to avoid precipitation of alumina, the material baffle is set on the central aluminum collection groove under interposing point, and the quality of baffle is the same with cathode material. Moreover, a serial step is taken to strengthen holding of cell for keeping energy balance of drained cells. In the numerical calculation, the cathode slope angle is 4?, and ACD is 3 cm, and other process condition is the same roughly as normal cells

Considering the symmetry, just calculates half cell, and the figure of analysis region is shown in Fig.1. In the coordinate, axis x points from side A to side B, and axis y points from underside of electrolyte to upper surface, and axis z points from end to middle. Taken uneven  multi-block structural grids, the whole analysis region is consisted of 42 184 units and 55 413 nodes, and the grids are encrypted between the two poles and the gaps of anodes.

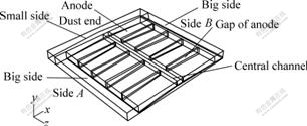
Fig.1 Analysis region of 156 kA drained cells (half cell)

3.2 Boundary condition and computation method

The cross section of half cell is defined as symmetry plane because the object of simulation is the half of cell, so does the interface of electrolyte and aluminum liquid. On the symmetry plane, the component of velocity vertical to the plane is 0, but also the derivatives of all variables along the normal of symmetry plane.

The anode gas releases in bubbles, and the equivalent diameter of bubble is 1 cm, and takes the underside of anode as the entrance. The coefficient of gas generation on unit area of anode in unit time can be calculated in following expression^[11]:

               (2)

where  q is coefficient of gas generation，m³/（s?m²）; J is density of anode current，A/m²；R is gas constant, 8.314 J/(mol?K)；T is thermodynamic temperature，K; F is Faraday constant，96 487 C/mol; p is atmosphere pressure，101 325 Pa.

Besides the symmetry plane and entrance, all of the other boundaries are wall. The upper surface of electrolyte is also defined as wall or says the degassing boundary condition for gas phase, that is ending the computation for bubble when it reaches the boundary, and simulates the free release of anode gas on electrolyte surface. On the wall, the non-slip boundary condition is taken.

Calculated by the commercial CFD software CFX-4.3, the improved method of inter phase slippage arithmetic (IPSA) of Spalding is established to compute the multi-phase model, and SIMPLEC arithmetic for velocity-pressure coupling. In order to get better astringency, the under-relaxation factor is adopted in this study.

3.3 Calculating results and analysis

The results of calculation are shown in Figs.2-7. The figures show the clear projection site of anode, and manage the scale and density of arrowhead in vectorgraph to display the flow field of electrolyte more clearly.

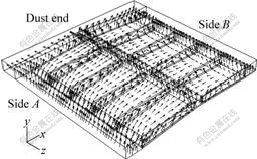
Fig.2 Flow field of anode gas between two poles (one fourth ACD away from bottom of anode)

Fig.3 Flow field of anode gas in anode gap

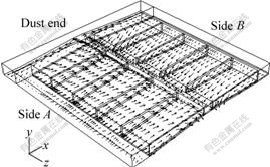
Fig.4 Flow field of electrolyte between two poles (one fourth ACD away from bottom of anode)

Fig.5 Flow field of electrolyte in central gap

Fig.6 Flow field of electrolyte in anode gap

Fig.7 Flow field of electrolyte near big side

3.3.1 Flow trend

From Figs.2 and 3, it can be seen that, different from the normal cells, in which the anode gas releases mainly from the adjacent anode gaps^[12-14], the anode gas of drained cells flows upwards along the slope mainly, and most of them flows into central channel on the top of slope, then releases upwards along the edge of anode. Obviously, it is the result of buoyancy. And some anode gas around the top of slope flow into anode gaps, and then release upwards along the edge of anode. For the present center point feeding system, the anode gas can release from the interposing hole sited in the central channel more easily.

From Figs.4 and 5, it can be seen that, the electrolyte which places between the poles flow into central channel along the slope driven by anode gas, and some get back into poles from central channel directly; some flow to end first, then get back into poles downwards the two big sides. From Fig.6, it can be seen that some electrolyte between two poles flow into anode gaps driven by anode gas, and move upwards, then flow to big side on the upper layer of anode gaps, and then flow downwards and back into poles. According to Fig.7 there is vertical cycle which flow upwards along the anode edge on big side, and then get back into poles along cell wall.

As shown in Fig.8, around the top of slope, there is local reflux for electrolyte which have flowed into anode gaps. Besides the gravity and the tow of anode gas, the electrolyte on the slope receives electromagnetic force which is accord with the movement of electrolyte, so there is no reflux. But for the electrolyte flowing into anode gaps, the action of electromagnetic force becomes weak greatly (most of current in anode is downward vertically, so the style should be same in electrolyte and exists merely in electrolyte region under the projection of anode, so the electromagnetic force acts in the same area merely). When the component of gravity along the slope is larger than the component of anode gas force, electrolyte would flow downwards along slope, and that is reflux. When electrolyte reflux reaches to a certain distance, it would flow back to central channel and big sides by the driven of upper upwelling. The reflux would be more obvious when the electrolyte is farther away from the end.

Fig.8 Reflux in anode gap

3.3.2 Scale of velocity

The average velocity of electrolyte is 8.3 cm/s, and the maximum is 59.5 cm/s. And the distribution of high velocity (larger than 20 cm/s) of electrolyte concentrates in anode gaps, and central channel, and the place where the big side is opposite to the anode gaps. That is because much anode gas and electrolyte flows into narrow anode gaps. The average velocity of anode gas is 23.2 cm/s, and the maximum is 61.1 cm/s.

Compared to normal cells^[15], the distribution of electrolyte velocity in drained cells is much even. The main reason is that there is small local cycle around anode, but the region which electrolyte cycle can agitate in drained cells is much larger. It is obvious that the electrolyte movement in drained cells is advantageous to eliminate concentration gradient and temperature gra- dient of electrolyte.

3.3.3 Turbulent intensity

The turbulent intensity is the strongest on the top of anode slope, central channel, and the place where the small side is opposite to central channel (the figures are neglected ). For center point feeding system, it is helpful for alumina to mix and diffuse.

3.4 Influence of cathode slope angle and ACD on electrolyte flow field

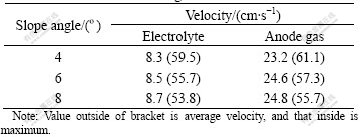
In order to understand the influence on electrolyte flow field of different cathode slope angle in drained cells, the flow field was calculated with angle 4?, 6?and 8?, respectively. There is no much change for general trend of electrolyte movement when the angle increases from 4? to  8?, but for electrolyte in the anode gaps, the local reflux becomes stronger gradually with the increase of cathode slope angle, and the maximum reflux even reaches to the half of slope length from the top in angle 8?(shown in Fig.9). That is because the component of electrolyte gravity along the slope increases with the increase of cathode slope angle, and then the reflux gets stronger gradually.

Fig.9 Reflux in anode gap with cathode slope angle of 8?

The velocity results with different cathode slope angles are listed in Table 1. It can be seen that with the increase of cathode slope angle, the average velocity of electrolyte and anode gas increases, but the maximum decreases. That is because the velocity of anode gas increases with the increase of angle, and then the average velocity of electrolyte increases, and more anode gas and electrolyte flows into central channel along the slope. So the anode gas and electrolyte flowing into anode gaps decreases, and the highest velocity appears around anode gaps, so the highest velocity of anode gas and electrolyte decreases. With the increase of cathode slope angle, the distribution of electrolyte velocity in drained cell becomes more even.

Table 1 Results of velocity with different cathode slope angles

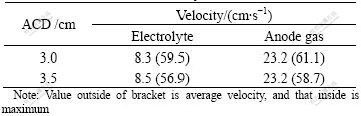
In order to study the influence on electrolyte flow field of ACD in drained cells, the electrolyte flow field was calculated in ACD of 3 cm and 3.5 cm, respectively. There is no much change for general trend of electrolyte movement, but for electrolyte in anode gaps, the local reflux becomes strong a little with the increment of ACD. That is because more electrolytes flow into anode gaps with the increase of ACD.

The velocity results with different ACD are listed in Table 2. It can be seen that the average velocity of electrolyte and anode gas increases with the increase of ACD, but highest velocity decreases. With the increase of ACD, the distribution of electrolyte velocity in drained cell becomes more even.

Table 2 Results of velocity with different ACD

4 Conclusions

1) Combined with simulation and stress analysis, the flow field of electrolyte and anode gas in drained cells is analyzed. Compared to normal cells, the distribution of flow field in drained cells is more even. The average and the maximum velocities of electrolyte are 8.3 cm/s and 59.5 cm/s, and the average and maximum velocities of anode gas are 23.2 cm/s and 61.1 cm/s, respectively.

2) Compared to normal cells, it is much easier to release anode gas and eliminate the concentration gradient and temperature gradient of electrolyte for center point feeding system, and better for mixing and diffusion of alumina in drained cells.

3) With increasing cathode slope angle and ACD, the flow field of electrolyte and anode gas become more even in drained cell.

References

[1] MEI Chi. Simulation and Optimization of the Nonferrous Metallurgy Furnaces[M]. Beijing: Metallurgical Industry Press, 2001: 150- 151.(in Chinese)

[2] WAHNSIEDLER W E. Hydrodynamic modeling of commercial hall-heroult cells[C]//Light Metals. Warrendale: TMS, 1987: 269- 287.

[3] PURDIE J M, BILEK M, TAYLOR M P, et al. Impact of anode gas evolution on electrolyte flow and mixing in aluminum electrowinning cells[C]//Light Metals. Warrendale: TMS, 1993: 355- 360.

[4] GAO Zhao-sheng, LI Guo-xun, SHEN Jian-yun. Mathematical modeling of bubble driven flows in a novel aluminum electrolysis cell[J]. Transactions of Nonferrous Metals Society of China, 1996, 6(2):37-40.

[5] BILEK M M, ZHANG W D, STEVENS F J. Modelling of electrolyte flow and its related transport process in aluminum reduction cells[C]// Light Metals. Warrendale: TMS, 1994: 323-331.

[6] ZHOU Li-xing. Fluid Mechanics of Multi-phase Turbulent Reaction[M]. Beijing: National Defence Industry Press, 2002: 78-101. (in Chinese)

[7] JIANG Chang-wei, MEI Chi, ZHOU Nai-jun, et al. Computation of 3 D magnetic field in prebaked cells using scalar voltage potential method and two scalar magnetic potentials method[J]. The Chinese Journal of Nonferrous Metals, 2003,13(4): 1021-1025.(in Chinese)

[8] ZHOU Nai-jun，MEI Chi, JIANG Chang-wei，et al. Coupled computation method of physics fields in aluminum reduction cells[J]. Transactions of Nonferrous Metals Society of China, 2003, 13(2): 431-437.

[9] ZHOU Zheng-ming. Thermo-Electric Coupled Simulation and Optimization of Drained Aluminum Reduction Cells[D]. Changsha: School of Energy Science and Engineering, Central South University, 2004.

[10] ZHOU Nai-jun, LI Jie, JIANG Chang-wei, et al．A kind of drained aluminum reduction cells with TiB₂ coating cathode. China: 200410023392.X[P]. 2004-07-06.

[11] SOLHEIM A, JOHANSEN S T, ROLSETH S, et al. Gas driven flow in Hall-Heroult cells[C]//Light Metals. Warrendale: TMS, 1989: 245-252.

[12] KOBBELTVEDT O, MOXNES B P. On the bath flow，alumina distribution and anode gas release in aluminum cells[C]//Light Metals. Warrendale: TMS, 1997: 369-376.

[13] ZORIC J, SOLHEIM A. On gas bubbles in industrial aluminum cells with prebaked anodes and their influence on the current distribution[J]. Journal of Applied Electrochemistry, 2000, 30: 787-794.

[14] LI Xiang-peng, LI Jie, LAI Yan-qing, et al. Physical modeling of gas induced bath flow in drained aluminum reduction cell[J]. Transactions of Nonferrous Metals Society of China, 2004, 14(5): 1017-1022.

[15] XIA Xiao-xia. Numerical Simulation on the Electrolyte Flow Field of Aluminum Reduction Cells[D]. Changsha: School of Energy Science and Engineering, Central South University, 2005.

(Edited by YANG You-ping)

Foundation item: Project(G1999064903) supported by the National Key Fundamental Research and Development Program of China

Received date: 2006-05-06; Accepted date: 2006-07-05

Corresponding author: ZHOU Nai-jun, Professor, PhD; Tel: +86-731-8836920; E-mail: njzhou@mail.csu.edu.cn