J. Cent. South Univ. (2016) 23: 2883-2895

DOI: 10.1007/s11771-016-3352-1

Weak thruster fault detection for AUV based on stochastic resonance and wavelet reconstruction

LIU Wei-xin(刘维新), WANG Yu-jia(王玉甲), LIU Xing(刘星), ZHANG Ming-jun(张铭钧)

School of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: When the bi-stable stochastic resonance method was applied to enhance weak thruster fault for autonomous underwater vehicle (AUV), the enhancement performance could not satisfy the detection requirement of weak thruster fault. As for this problem, a fault feature enhancement method based on mono-stable stochastic resonance was proposed. In the method, in order to improve the enhancement performance of weak thruster fault feature, the conventional bi-stable potential function was changed to mono-stable potential function which was more suitable for aperiodic signals. Furthermore, when particle swarm optimization was adopted to adjust the parameters of mono-stable stochastic resonance system, the global convergent time would be long. An improved particle swarm optimization method was developed by changing the linear inertial weighted function as nonlinear function with cosine function, so as to reduce the global convergent time. In addition, when the conventional wavelet reconstruction method was adopted to detect the weak thruster fault, undetected fault or false alarm may occur. In order to successfully detect the weak thruster fault, a weak thruster detection method was proposed based on the integration of stochastic resonance and wavelet reconstruction. In the method, the optimal reconstruction scale was determined by comparing wavelet entropies corresponding to each decomposition scale. Finally, pool-experiments were performed on AUV with thruster fault. The effectiveness of the proposed mono-stable stochastic resonance method in enhancing fault feature and reducing the global convergent time was demonstrated in comparison with particle swarm optimization based bi-stochastic resonance method. Furthermore, the effectiveness of the proposed fault detection method was illustrated in comparison with the conventional wavelet reconstruction.

Key words: autonomous underwater vehicle (AUV); thruster; weak fault; particle swarm optimization (PSO); mono-stable stochastic resonance; wavelet reconstruction

1 Introduction

Autonomous underwater vehicles (AUV) operate in complex and unknown marine environment without tether. Thrusters are one of the most common and most important sources of faults [1]. No matter what the evolvement trend of thruster fault is, the thruster fault generally occurs from weak fault [2]. Therefore, the study on weak thruster fault diagnosis is significant to improve the intelligence of AUV and guarantee AUV’s safety and reliability [3]. It is also one of the research focuses of fault diagnosis for AUV [4].

In general, thruster fault diagnosis methods can be classified into two types: qualitative one and quantitative one [5]. The qualitative one just can give the probability interval of fault occurrence and the interval is rough, which results in low diagnosis accuracy [6-7]. The quantitative methods can be divided into two types: analytical model and data-driven [5]. The diagnosis performance based on analytical model depends on the accuracy of the mathematic model [8-9]. However, since it is difficult to construct an accurate AUV dynamic model in the ocean environment, the diagnosis accuracy is not satisfactory based on analytical model [10-11]. The data-driven methods are more suitable for thruster fault identification, because the accurate AUV dynamic model is not required in the kind of method [12-13].

In the study on thruster fault diagnosis, the authors found the following phenomenon. In the case with serious thruster fault (>10%), the external disturbance had a little impact on results of fault diagnosis, and the data-driven diagnosis methods could timely and accurately detect thruster fault. However, in the case with weak thruster fault (≤10%), the external disturbance has large effect on results of fault diagnosis, and the data-driven diagnosis methods could not timely and accurately detect thruster fault. Sometimes, undetected fault or false alarm may occur.

In order to detect weak thruster fault timely and accurately, the paper focuses on two problems: the enhancement of weak thruster fault feature and the selection of optimal wavelet reconstruction scale.

In the former researches, the authors had ever studied fault feature enhancement method based on bi-stochastic resonance [14]. However, when the method was directly applied to the case with weak thruster fault, the feature of thruster fault was enhanced still, but the thruster fault feature was less than that of external disturbance. Thus, the performance of enhancing weak thruster fault feature was not satisfactory.

On the basis of the above experiment research, as for the problem that the weak thruster fault feature enhancement was not satisfactory based on the bi-stable stochastic resonance method, fault feature enhancement based on the mono-stable stochastic resonance was proposed. Since AUV’s state and control variables were aperiodic [14], the bi-stable potential function was changed to mono-stable potential which was more suitable for the aperiodic cases. During the process of stochastic resonance, in order to simultaneously adjust the parameters of stochastic resonance and reduce the global convergent time, an improved particle swarm optimization method was developed by changing the linear inertial weighted function as nonlinear one with cosine function.

When the conventional wavelet reconstruction method was adopted to detect weak thruster fault, the authors found that wavelet reconstruction value of thruster fault may be less than that of external disturbance. The modulus maximum after wavelet reconstruction may be caused by external disturbance rather than thruster fault. It needed to select optimal scale with most fault information to conduct wavelet reconstruction.

Motivated by the above-presented analysis, with respect to the problem that undetected fault or false alarm may occur based on the conventional wavelet reconstruction, the paper proposed weak thruster fault detection method based on the integration of stochastic resonance and wavelet reconstruction. At first, fault feature was enhanced by mono-stable stochastic resonance. And then, it selected the optimal scale to conduct wavelet reconstruction based on the wavelet coefficients after enhancing fault feature.

Finally, pool-experiments were performed on Beaver 2 AUV with thruster fault to acquire experiment data. The paper compared the developed method and particle swarm optimization based bi-stochastic resonance in terms of fault feature enhancement and global convergent time. In addition, in comparison with the conventional wavelet reconstruction method, the performances of the developed method were compared in terms of whether the thruster fault could be detected without false alarm.

2 Thruster fault feature enhancement

2.1 Fault feature enhancement based on mono-stable stochastic resonance

The authors had ever studied thruster fault feature enhancement based on bi-stable stochastic resonance [14], which had good performance for the serous thruster fault. However, when the method was directly applied to the case with weak thruster fault, fault feature enhancement was not satisfactory. On the basis of the former research [14], the paper further investigated weak thruster fault feature enhancement method based on stochastic resonance.

Nowadays, some improved bi-stable stochastic resonance had been proposed, including ant colony optimization based [15], knowledge based [16]. These methods greatly enhanced the fault feature for periodic signals. However, when these methods were directly applied to enhance thruster fault feature, the enhancement performance was not obvious.

As for the above problem, on the basis of stochastic resonance theory [17-18], the authors thought that the performance of bi-stable stochastic resonance depended on the transition of Brownian particle driven by the periodic signals. However, in the case of AUV aperiodic signals, the Brownian particle only could move in the single potential well, without transition from one potential well to another. Thus, the external disturbance signals could not adequately transit into fault signals, which resulted in the fact that the fault feature enhancement was not obvious based on bi-stable stochastic resonance with potential well.

Based on the analysis, the paper proposed weak thruster fault feature enhancement method based on mono-stable stochastic resonance, in order to enhance weak thruster fault feature. In the developed method, the conventional bi-stable potential function was changed to a mono-stable potential function suitable for AUV aperiodic signals. In this way, it avoided the Brownian particle transition in the bi-stable stochastic resonance and improved the enhancement performance.

The steps of the proposed method were summarized as follows:

1) Construct stochastic resonance system;

2) Select assessment index of stochastic resonance;

3) Select the input of stochastic resonance system;

4) Extract fault feature from the output of stochastic resonance system.

In the above steps, the assessment index of stochastic resonance was the same as that in the authors’ work in Ref. [14]. Steps 3) and 4) were the same as those in Ref. [17]. Step 1) was different from that in Ref. [17]. In Ref. [17], Step 1) was to construct bi-stable stochastic resonance system with two steady states and one potential well. But in the developed method, Step 1) was only to construct mono-stable stochastic resonance system with one steady state and no potential well. Now, Step 1) would be detailed as follows.

At first, a bi-stable stochastic resonance model was given [17].

                      (1)

where was the first-order derivative of the system output; s(t) was the system input; n(t) was the noise; V′(x) was the first-order derivative of the bi-stable potential function V(x), and the expression of V(x) was presented as Eq.(2) [17].

                        (2)

where c and d were the system parameters and non- negative, grespectively.

In order to transmit more energy of the external disturbance into fault signal, the paper developed weak thruster fault feature enhancement method based on mono-stable stochastic resonance. In the improved method, the mono-stable potential function U(x) was developed to replace the bi-stable potential function V(x). The detailed expression was shown as Eq. (3)

                          (3)

where a was offset coefficient and non-negative; b was system parameter and positive.

According to replacing the bi-stable potential function V(x) by the developed mono-stable potential function U(x), the new stochastic resonance system was obtained.

In order to theoretically illustrate the advantage of the constructed mono-stable stochastic resonance system in terms of achieving stochastic resonance of aperiodic signals, in comparison with bi-stable stochastic resonance system, the paper analyzed the difference of these two systems. According to Eqs. (2) and (3), the potential functions of these two systems are shown in Fig. 1.

The stable-state point and potential well in Fig. 1 were analyzed comparatively. From Fig. 1, in the bi-stable stochastic resonance system, the potential function had two stable-state points and the height of potential well was In the mono-stable stochastic resonance system, the potential function had only one stable-state point and there was no potential well. In comparison with the bi-stable stochastic resonance system, there was no need to transit over the potential well for the Brownian particle driven by the AUV aperiodic signals based on the constructed mono-stable stochastic resonance. In this way, it was beneficial to transition of the external disturbance signals into aperiodic fault signals and enhancement of the fault feature.

Fig. 1 Potential functions in mono-stable/bi-stable stochastic resonance systems

In general, thruster fault of AUV indicates the part loss of effectiveness of thruster output [9]. The state variables affected by main thruster fault include surge velocity, surge acceleration and yaw angle, among which surge velocity and surge acceleration belong to a type of variable in essence. In the paper, the surge acceleration was not selected to detect source of thruster fault due to the great variance of its value. The authors have ever researched fusion fault diagnosis method based on the combination of surge velocity and yaw angle, where it was difficult to determine the weighted coefficient matrix [13]. Therefore, the paper only selected surge velocity to detect source of weak thruster fault.

When a fault occurred in certain thruster, the surge velocity would be varied relatively greatly because of the impacts of thruster fault and external disturbance such as ocean current. In terms of weak thruster fault, both wavelet coefficients of the fault feature and external disturbance were relatively small. As a result, it only estimated the suppression threshold when dealing with surge velocity based on the conventional methods, such as wavelet analysis, to reduce the impact of external disturbance. The wavelet coefficient which was higher than that threshold would be regarded as fault feature; otherwise, it would be considered external disturbance. However, the number of points with the former case always were more than one, including the influence of both fault feature and external disturbance, which would result in the fact that it was difficult to distinguish weak thruster fault from external ocean current based on wavelet analysis [14].

The mono-stable stochastic resonance was developed to enhance fault feature in the paper. Different from wavelet transformation method addressing problems from signal processing, the proposed method is to handle fault diagnosis from energy transition, which was to transit energy of external disturbance to that of fault feature. A aperiodic mono-stable stochastic resonance model was constructed considering the aperiodic feature of surge velocity, which was the input of the model. The Brownian particle driven by fault signal oscillate rounded the steady point in the well; the Brownian particle driven by external disturbance moved randomly. The energy of fault signal was transmitted to the potential energy of Brownian particles. According to adjusting the height of the well or changing the shape of the well, the probability of which those Brownian particles with random motion overlapped those with ordered motion, the energy, would be increased by the rising probability, in other words, the height of oscillation. Due to the total potential energy was fixed, the energy of random motion was declined, which indicated that the fault feature was enhanced while the feature of external disturbance was decreased.

Pool-experiments would be presented in Section 4.2 to present comparatively the performance of fault feature enhancement based on the bi-stable/mono-stable stochastic resonance system, respectively.

2.2 Improved particle swarm optimization based on nonlinear weighting value

During the process to achieve stochastic resonance of AUV aperiodic signals, the parameters of stochastic resonance system were needed to be optimized simultaneously [19]. With respect to the problem, the optimization method based on particle swarm was classical [20]. However, when particle swarm optimization based on linear inertial weighted function was adopted to adjust the parameters of stochastic resonance system, the authors found that it took long time to achieve the global convergence. In order to real-time adjust AUV fault diagnosis system in the future, the paper investigated the problem how to reduce the global convergent time.

There were some improved methods about particle swarm optimization, including stochastic black hole [21] and alternate prey [22]. These methods could avoid premature convergence. However, when these methods were applied to optimize simultaneously the parameters of stochastic resonance system driven by AUV aperiodic signals, there was no obvious reduction in the global convergent time.

Based on particle update theory [20] and experiment data, the authors thought that the particle swarm optimization based on linear inertial weighting function did not consider the following nonlinear change trend. In the beginning, the distance between particle and the optimal solution was large; but at the end, the distance was small. Thus, it was more probable that the particle transited over the optimal solution. That is to say, at the end of optimization, the particle oscillated near the optimal solution, increasing the global convergent time.

In order to reduce the global convergent time, the paper developed particle swarm optimization method based on nonlinear inertial weighting function. In the developed method, the linear inertial weighting function was changed to nonlinear inertial weighting function by adding the cosine function. It was beneficial to reduce the global convergent time in the process of optimizing simultaneously parameters of stochastic resonance system.

The steps of the developed method were summarized as follows:

1) Population initialization;

2) Construct stochastic resonance system;

3) Determine the evaluation method for the individual;

4) Update particle based on nonlinear inertial weighting function;

5) Determine whether the optimization stops based on optimization termination condition;

6) Output the optimal parameters.

In the above steps, Step 1, Step 3, Step 5 and Step 6 were the same as those in Ref. [16]. Step 2) was Ref. in Subsection 2.1. Step 4) was different from that in Ref. [16], namely, the update method of particle was different. In the conventional particle swarm optimization method, the linear inertial weighting function was adopted to update the particle. However, in the developed method, the update of particle was accomplished based on the improved nonlinear inertial weighting function. The detail of step d was presented in the following.

In the conventional particle swarm optimization method, the flying speed V_i(t+1) and position X_i(t+1) were updated as Eqs. (4) and (5) [16].

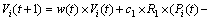
         (4)

                      (5)

where V_i(t+1) was the updated flying speed of particle; X_i(t+1) was the updated position of particle; c₁ and c₂ were learning factors; R₁ and R₂ were random within the interval of [0, 1]; w(t) was inertial weighting coefficient.

In Eq. (4), the inertial weighting coefficient was obtained from Eq. (6) in the conventional particle swarm optimization method [1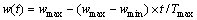6].

              (6)

where w_max and w_min were the upper and lower of the inertial weighting coefficient; t was the evolutional generation; T_max was the maximum evolutional generation.

In order to reduce the particle oscillation caused by the linearly decreasing weight and the global convergent time, on the basis of the conventional particle swarm optimization, the paper developed an improved updated method for particle based on the nonlinearly weight. A cosine function was added into Eq. (6) to obtain the nonlinearly inertial weight, as shown in Eq. (7).

                      (7)

where w_c(t) was the inertial weighting coefficient based on the improved method.

In order to theoretically illustrate the advantage of the improved method in terms of reducing the global convergent time, in comparison with the conventional particle swarm optimization, the comparative figure about the inertial weight was obtained from Eqs. (6) and (7), as shown in Fig. 2.

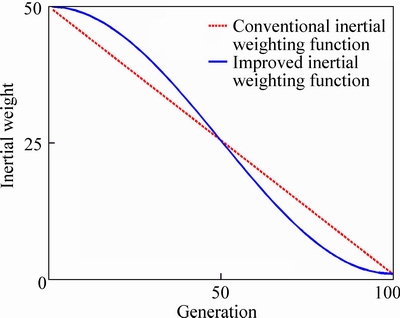
Fig. 2 Inertial weighting function

The adjustment trend of the inertial weight in Fig. 2 was analyzed comparatively. From Fig. 2, the inertial weight was linearly decreasing as the evolutional generation increased. However, the inertial weight was nonlinearly decreasing as the evolutional generation increased. To be specific, the inertial weight decreased slowly in the beginning, and then the weight decreased quickly to make the particles converge to the optimal solutions quickly. Finally, the weight decreased slowly again, avoiding the oscillation caused by quickly decreasing and reducing the global convergent time.

Pool-experiments would be presented in Section 4.2 to present comparatively the performances of reduction of the global convergent time based on these two methods, respectively.

3 Weak thruster fault detection based on stochastic and wavelet reconstruction

In order to detect thruster fault for AUV subject to ocean current, the authors had ever studied the thruster fault detection method based on wavelet reconstruction [23], which had good performance in the case of serious thruster fault. However, when the method was directly applied to detect weak thruster fault, the authors found that the feature of weak thruster fault was close to that of external disturbance. The wavelet reconstruction value of weak thruster fault may be less than that of external disturbance, which would cause undetected fault or false alarm, when wavelet reconstruction was applied to detect thruster fault,

Nowadays, some improved wavelet reconstruction had been proposed, including optimized wavelet basis function [24], continuous wavelet transformation [25]. These methods had obtained good performance in detecting weak fault with periodic feature for rotating machines such as rolling bearing. However, when these methods were directly used to detect weak thruster fault for AUV, false alarm or undetected fault may occur.

With respect to the above problem, on the basis of wavelet theory [26], it could be found that the conventional wavelet reconstruction method was based on the fact that the feature of external disturbance decreased and the feature of fault increased as the wavelet decomposition scale was increased. However, in the case of weak thruster fault, the feature of weak thruster fault was close to that of external disturbance. The fault feature indeed increased as the wavelet decomposition scale increased, but the feature enhancement of fault was unobvious. Furthermore, restricted by the wavelet decomposition scale, the feature of weak thruster fault did not obviously overweigh that of external disturbance after multi-resolution wavelet decomposition. Therefore, the false alarm or undetected fault may occur when conventional wavelet reconstruction method was applied to detect weak thruster fault.

On the basis of the above presented analysis, a weak thruster fault detection method was proposed based on the combination of stochastic resonance and wavelet reconstruction. In the proposed method, wavelet entropy of wavelet coefficients corresponding to each decomposition scale was calculated at first, and then the optimal wavelet scale was determined by selecting the wavelet scale with the minimum wavelet entropy. Finally, the wavelet reconstruction was conducted to detect weak thruster fault based on the wavelet coefficient corresponding to the optimal wavelet reconstruction scale.

The steps of the proposed method were summarized as follows:

1) Obtain AUV signals based on moving-window scheme;

2) Enhance feature of thruster fault based on stochastic resonance theory;

3) Conduct discrete wavelet decomposition;

4) Determine the optimal reconstruction scale based on the wavelet entropies;

5) Conduct wavelet reconstruction and detect thruster fault.

In the above steps, Step 1), Step 3), Step 5) were the same as the steps in Ref. [23]. Step b was given in Section 2.1. Step 4) was different from that in the Ref. [23], namely, the determination method of wavelet reconstruction scale was different. In the conventional wavelet reconstruction, the wavelet detailed coefficient corresponding to the highest decomposition scale in discrete wavelet decomposition was adopted to detect thruster fault. However, in the proposed method, the wavelet coefficient after feature enhancement was used to calculate wavelet Shannon entropy at first, and then the optimal reconstruction scale was determined by comparing all the wavelet Shannon entropies. Finally, thruster fault was detected by calculating wavelet coefficient corresponding to the optimal reconstruction scale. The detailed process about Step 4) was presented as follows.

In the conventional wavelet reconstruction method, the discrete wavelet decomposition was conducted as Eq. (8) [23].

             (8)

where C_j(k) was wavelet approximation coefficient; D_j(k) was the wavelet detailed coefficient; s(n) was the control and state variables of AUV; < > denoted inner product operation; φ(n) was the wavelet scale function; ψ(n) was wavelet basis function.

In the conventional wavelet reconstruction method, the wavelet coefficients corresponding to the highest decomposition scale were used to detect thruster fault, without considering the variance among the fault information under different scales. The method assumed that most of the fault information was contained in the wavelet coefficients under the highest scale.

On the basis of wavelet reconstruction, a weak thruster fault detection method was proposed by integrating stochastic resonance and wavelet reconstruction. Instead of directly making use of the wavelet coefficients corresponding the highest decomposition scale to detect thruster fault, in the proposed method, at first wavelet coefficients were calculated based on discrete wavelet decomposition; then the wavelet Shannon entropies were calculated for all wavelet coefficients under all decomposition scales; finally, the optimal reconstruction scale was determined by comparing wavelet Shannon entropies. The detailed of step d was presented in the following.

1) Probability distribution

After obtaining wavelet detailed coefficients for all decomposition scale according to discrete wavelet decomposition, these detailed coefficients were treated as independent signals W with the length N. At first, the detailed coefficients W were conducted as probability distribution sequence and the detailed means was shown in Eq. (9) [24].

                           (9)

where p_i was probability distribution value corresponding to the ith wavelet coefficient; W(i) was wavelet coefficient sequence.

2) Calculation of wavelet entropy

According to Eq. (10), the wavelet entropy was calculated based on the obtained probability distribution value p_i [27].

                         (10)

where H(P) was wavelet entropy.

3) Determination of optimal reconstruction scale

The optimal reconstruction scale corresponding to the minimum wavelet entropy was determined. Wavelet reconstruction with single scale method was given in Ref. [27]. According to the optimal reconstruction scale and wavelet reconstruction with single scale method, the wavelet reconstruction was conducted. Then, the time point corresponding to the modulus maximum after wavelet reconstruction was treated as the detected fault occurrence.

Pool-experiments would be presented in Section 4.3 to present comparatively the performance of fault detection based on the developed method and the conventional wavelet reconstruction method, respectively.

4 Experiment verification

4.1 AUV prototype and thruster fault simulation

Beaver 2 AUV was used to perform experiments. And according to the thruster fault simulation method, which had been studied in the former research, the fault is simulated in HT1 thruster during experiments to demonstrate the effectiveness of the developed method. The AUV prototype, experiment condition, and thruster fault simulation were presented as follows.

1) AUV prototype

Beaver 2 AUV was developed by the authors’ lab in 2014, shown in Fig. 3. Its dry mass was 50 kg. And the maximum longitude speed could be 0.65 m/s. The sensor system consisted of NavQuest_600_Micro Doppler Velocity Log, HMR3000 Digital Compass and CYT-151 Depth Gauge. In horizontal plane, two pairs of thrusters were configured in Beaver 2 AUV, a pair of main thrusters along the longitude line and the other along the sway line. In vertical plane, a pair of thrusters was configured to control depth. The thruster distribution is shown in Fig. 4.

Fig. 3 Beaver 2 AUV

Fig. 4 Thruster distribution

2) Experiment condition

A small device used to produce ocean current was designed by the authors’ lab. The device consists of four thrusters (24 V, 200 W) in the horizontal plane. Ocean current was simulated by the device in the range of AUV operation. Experiment condition and the device were presented in Fig. 5. The size of pool is 50 m, 30 m, 10 m in the length, width and depth, respectively.

During experiments, a current log with 0.25 Hz was adopted to measure the flow and ocean current. The measurement result is shown in Fig. 6.

In Fig. 6, the device was located in Point A, and AUV was driven along the vector B. The value of ocean current in Fig. 6 was an average value.

3) Thruster fault simulation

According to the former research about thruster fault, in this work, the thruster fault was simulated as follows:

Fig. 5 Experiment condition and device

Fig. 6 Magnitude of ocean current in operation area

                      (11)

where U′ was the control voltage to thruster after fault occurrence; U was the theoretical control voltage; λ was the magnitude of thruster fault.

Equation (11) represents the variance of control voltage caused by thruster fault. The different magnitudes of thruster fault can be simulated by changing the value of λ.

4.2 Comparative verification on fault feature enhancement and global convergent time

4.2.1 Comparative verification on fault feature enhancement

Pool-experiment was performed on Beaver 2 AUV to demonstrate the effectiveness of the developed mono- stable stochastic resonance method on the fault feature enhancement.

Beaver 2 AUV was driven to track the longitude speed with 0.3 m/s and yaw angle 230°. In addition, from the 250th step to the 500th step, different magnitudes of fault occurred in HT1 thruster, including 10%, 8% and 5%.

1) Experiment process and results in experiment of fault feature enhancement

According to the mono-stable stochastic resonance system constructed in Section 2.1 and optimized parameters of stochastic resonance system given in section 2.2, AUV longitude speed was chosen as input of stochastic resonance system; then, the output of stochastic resonance system and AUV longitude speed were normalized and then were conducted discrete wavelet decomposition. Finally, the absolute values of wavelet detailed coefficients corresponding to the highest decomposition scale were extracted as fault feature.

Taking 5% thruster fault as an example to illustrate experiment results, the longitude speed in the presence of 5% thruster fault is shown in Fig. 7. And fault feature extraction results are shown in Fig. 8 under the conditions of mono-stable/ bi-stable stochastic resonance and raw signals.

Fig. 7 Longitude speed in the presence of 5% fault in HT1 thruster

Fig. 8 Extracted fault feature in the presence of 5% fault in HT1 thruster

In order to present the fault feature and external disturbance feature after enhancing thruster fault, the two kinds of feature values from Fig. 8 are tabulated in Table 1.

Table 1 Fault feature and external disturbance feature after enhancing thruster fault

From Table 1, the feature value corresponding to Sequence 8 was selected as fault feature value and others were treated as external disturbance feature values.

As can be seen from Fig. 8 and Table 1, the modulus maximum of wavelet coefficient was 2.3978 based on the proposed method, being enhanced by 171.70% and 130.56%, respectively, compared with that of raw signal (0.8826) and that of wavelet coefficient based on bi-stable stochastic resonance method (1.0400). As a result, the enhancement performance of thruster fault feature was increased by 153.87%, compared with the that of bi-stable stochastic resonance method. Feature relative value was 4.7855 based on the proposed method, being enhanced by 117.05% and 86.59%, respectively, compared with that of raw signal (2.2048) and that of wavelet coefficient based on bi-stable stochastic resonance method (2.5647). As a result, the enhancement performance of thruster fault feature relative value was increased by 153.87%, compared with the that of bi-stable stochastic resonance method.

2) Comparative analysis on fault feature enhancement

As usual the modulus maximum was adopted to assess the performance of fault feature enhancement. However, in practical fault diagnosis, besides the modulus maximum, feature relative value [28], that is the modulus maximum to average feature ratio, was also needed to be compared. In the following, these two assessment indexes including the modulus maximum and feature relative value were adopted to demonstrate the performance of fault feature enhancement.

(a) Modulus maximum

In order to clearly illustrate the comparative performance based on the developed mono-stable stochastic resonance method and bi-stable stochastic resonance method, the data in Fig. 8 are tabulated in Table 2.

Table 2 Enhancement results about modulus maximum based on different methods

In the cases of different magnitude of thruster faults (10%, 8%, 5%), in comparison with the MM of raw signal, the MM of fault feature has been enhanced by 9.58%, 30.65%, 17.83%, respectively, based on BSR; and the MM of fault feature has been enhanced by 54.55%, 100.33%, 171.70%, respectively, based on the developed one. In comparison with the results of BSR, the MM of fault feature has been enhanced by 44.97%, 69.68%, 153.87%, respectively, based on the developed mono-stable stochastic resonance method. These results show that the developed mono-stable stochastic resonance method could acquire more obvious performance in enhancing the MM of fault feature, compared to BSR.

Furthermore, the paper paid more attention to the weaker thruster fault. In the case of 5% thruster fault, the MM of fault feature is increased by 17.83% after BSR than that of RS; however, the MM of fault feature is increased by 171.70% after the developed mono-stable stochastic resonance method than that of RS. In comparison with the results of BSR, the MM of fault feature has been enhanced by 153.87% based on the developed mono-stable stochastic resonance method. The results illustrate that the developed mono-stable stochastic resonance method could acquire more obvious performance in enhancing the MM of fault feature in the case of weaker thruster fault, compared to BSR.

(b) Feature relative value

In order to clearly illustrate the comparative performance based on the developed mono-stable stochastic resonance method and bi-stable stochastic resonance method, at first feature relative values based on these two methods are calculated and tabulated in Table 3.

In the cases of different magnitude of thruster faults (10%, 8%, 5%), in comparison with RS, the FRV of fault feature has been enhanced by 2.65%, 17.47%, 16.32%, respectively, based on BSR; and the FRV of fault feature has been enhanced by 29.51%, 67.81%, 117.05%, respectively, based on the developed. In comparison with the results of BSR, the FRV of fault feature has been enhanced by 26.86%, 50.34%, 100.73%, respectively, based on the developed mono-stable stochastic resonance method. These results show that the developed mono- stable stochastic resonance method could acquire more obvious performance in enhancing the FRV of fault feature, compared to BSR.

Table 3 Enhancement results about feature relative value based on different methods

Furthermore, the paper paid more attention to the weaker thruster fault. In the case of 5% thruster fault, the FRV of fault feature increases by 16.32% after BSR than that of RS; how, the FRV of fault feature increases by 117.05% after the developed mono-stable stochastic resonance method than that of RS. In comparison with the results of BSR, the FRV of fault feature has been enhanced by 100.73% based on the developed mono-stable stochastic resonance method. The results illustrate that the developed mono-stable stochastic resonance method could acquire more obvious performance in enhancing the FRV of fault feature in the case of weaker thruster fault, compared to BSR.

In order to diagnose the weak thruster fault, from the perspective of energy transition, the paper discussed the method to enhance the distinction of fault feature and external disturbance feature, which is the core step of weak thruster fault. According to wavelet theory, the fault feature would be enhanced and external disturbance feature would be decreased with the increase of wavelet resolution scale. Technically, wavelet threshold method could be applied. To be more detailed, the threshold value corresponding to each wavelet resolution scale was calculated at first. And then, in the case where feature values were lower than threshold, the feature would be set zero while in the other case, the feature remained fixed. As a result, the distinction of fault feature and external disturbance feature were to be enhanced. On the other hand, it also could attempt to investigate the method combination of stochastic resonance theory and wavelet threshold. After enhancing fault feature and acquiring the exact position of fault feature, wavelet threshold method was to enhance the distinction of fault feature and external disturbance feature, which would provide a better situation for weak thruster diagnosis.

4.2.2 Comparative verification on global convergent time

Based on the parameters of stochastic resonance system given by the improved particle swarm optimization method and the conventional particle swarm optimization method, respectively, the paper calculated the global convergent time and demonstrated the effectiveness of the improved method in reducing the global convergent time.

According to the steps given in section 2.2, the parameters of stochastic resonance system were optimized simultaneously. Figures 9 and 10 show the convergent line of the optimal solution and variance of population fitness, based on the improved method and the conventional particle swarm optimization method, respectively.

Fig. 9 Optimization results based on developed method:

In order to clearly illustrate the comparative performance based on the improved method and the conventional particle swarm optimization method, the data in Fig. 9 and Fig. 10 are tabulated in Table 4.

1) Desired precision and global convergent time

In the work, the termination condition about optimization was given as follows: The maximum of generation was 100 or the variance of population fitness was less than 10^-3.

Fig. 10 Optimization results based on conventional method:

Table 4 Optimization results based on different methods

From Table 4, in the case of different magnitudes (10%, 8% and 5%) of thruster fault, the variances of population fitness are less than 10^-3 within a maximum of generation, and the needed generations are 74, 77, 72, respectively, based on the improved method.

From Table 4, in the case of different magnitudes (10% and 8%) of thruster fault, the variances of population fitness are less than 10^-3 within a maximum of generation, and the needed generations are 89 and 91, respectively, based on the conventional particle swarm optimization method, which are more than those in the improved method. However, in the case of 5% thruster fault, within the maximum of generation, the variance of population fitness is still more than 10^-3.

The experiment results show that the improved method has greater advantage in reaching the desired precision and reducing global convergent time than the conventional particle swarm optimization method.

2) Global optimal solution

According to the GOS in Table 4, in the cases of 10%, 8% and 5% thruster fault, the assessment indexes about the GOS have been improved by 10.40%, 33.73% and 10.54%, in comparison with the conventional particle swarm optimization.

The results indicate that the improved method has great advantage in the GOS than the conventional particle swarm optimization.

4.3 Comparative verification on weak thruster fault detection

Pool-experiment was performed on Beaver 2 AUV to demonstrate the effectiveness of the developed fault detection method by integrating stochastic resonance and wavelet reconstruction on the weak thruster fault detection.

Beaver 2 AUV is driven to track with the longitude speed 0.3 m/s and yaw angle 230°. In addition, from the 75th step to the end, 5% thruster fault occurred in HT1 thruster.

1) Experiment process and results in experiment of fault detection

At first, according to the steps given in Section 2.1, the mono-stable stochastic resonance system was constructed to enhance fault feature. And then, according to the steps given in Section 3, discrete wavelet decomposition was conducted for the output of stochastic resonance system. Finally, wavelet Shannon entropies were calculated and the optimal reconstruction scale was determined to reconstruct single-branch wavelet.

The HT1 thruster voltage in the case of 5% thruster fault is shown in Fig. 11. The wavelet Shannon entropies corresponding to all reconstruction scales are tabulated in Table 5 based on DM and CM. Figure 12 shows the comparative result about fault detection based on these two methods.

In order to clearly illustrate the comparative performance based on DM and the conventional wavelet reconstruction method, the data in Fig. 11 and Fig. 12 are tabulated in Table 6. It should be noticed that the results in the cases of 10% and 8% thruster fault are tabulated in Table 6.

2) Comparative analysis on performance of fault detection

At first, the fault detection was simply described. In Ref. [26], the time point corresponding to the MM was chosen as the time point of fault occurrence.

Fig. 11 Voltage of HT1 thruster in the presence 5% fault

Table 5 Wavelet Shannon entropies corresponding to different decomposition scales

Fig. 12 Comparative results of fault detection

Table 6 Comparative results about fault detection based on different methods

However, in the former research the authors found that asymmetric wavelet basis function would made the data have some delay, which caused that the time point corresponding to the MM was later than the time point of fault occurrence. But the delay was less than 10 steps, which meant that if the MM occurred over 10 steps after the time point of fault occurrence, the MM was not caused by this thruster fault. So, we compared the time points corresponding to the MM and fault occurrence, and the fault was detected if the delay was less than 10 steps.

According to the above-presented fault detection method, from Table 6, in the cases of 10% and 8% thruster fault, these two methods all could detect thruster fault.

However, in the case of 5% thruster fault, the time point of fault occurrence is at the 75th step. The time point corresponding to the MM is at 80th step based on DM, where the delay is 5 steps. That is to say, DM can detect the 5% thruster fault. Within 10 steps after the time point corresponding to thruster fault, the MM did not occur based on CM, which indicates that the conventional method did not detecte the 5% thruster fault.

Further analyzing Table 6, at the 166th step after the time point corresponding to thruster fault, MM occurred based on CM. Based on the conclusion in Ref. [23], the MM is not caused by the thruster fault occurring at the 75th step. The enlarged figure about the data near the 241st step of Fig. 11 is given in Fig. 13.

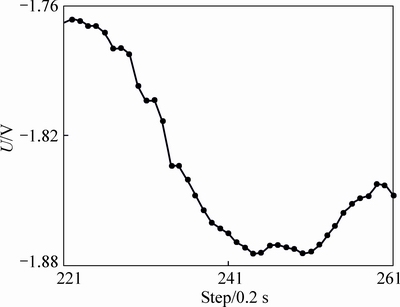
Fig. 13 Enlarge view of voltage of HT1 thruster in the presence 5% fault

From Fig. 13, the voltage is changed suddenly from -1.813 V to -1.834 V at the 234th step. The change is delayed 7 steps after the asymmetric wavelet basis function, namely, the time point corresponding to the MM is at 241st step and CM thinks that a fault occurred in this time point. However, in experiment condition, there are no other new thruster faults near the 234th step. So, the authors thinks, the MM is caused by external disturbance, rather than thruster fault, namely, false alarm occurred in the experiment based on CM.

The experiment results show that DM could detect 10%, 8% and 5% thruster faults without false alarm. The conventional method could detect 10% and 8% thruster faults without false alarm, but it could not detect 5% thruster fault, and false alarm also occurred. It can be concluded that DM could obtain greater performance of weak fault detection.

5 Conclusions

1) In order to enhance the weak thruster fault feature, mono-stable stochastic resonance method was proposed. The experiment results show that in the cases of 10%, 8% and 5% thruster fault, in comparison with BSR, the MM based on the improved method has been enhanced by 44.97%, 69.68% and 153.87%, respectively, and the FRV has been enhanced by 26.86%, 50.34% and 100.73%, respectively. The above experiment results indicate that MSR has greater advantage of enhancing fault feature than BSR in the cases of different thruster fault. And in the weaker thruster fault, the advantage would be more obvious.

2) In order to reduce the global convergent time, an improved particle swarm optimization method was developed, where the particle was updated based on nonlinear inertial weight. The experiment results show that in the cases of 10%, 8% and 5% thruster fault, in comparison with the conventional particle swarm optimization method, the improved method has superior performance in reaching the desired precision and reducing the global convergent time.

3) In order to resolve the problem of the conventional wavelet reconstruction method that false alarm or undetected fault may occur sometimes, a weak thruster fault detection method by integrating stochastic resonance and wavelet reconstruction was developed. The experiment results show that DM could detect thruster faults without false alarm in the cases of 10%, 8% and 5% thruster fault. The conventional method could detect 10% and 8% thruster faults without false alarm; but it could not detect 5% thruster fault, and false alarm also occurred. It can be concluded that DM could obtain greater performance of weak fault detection.

4) In terms of fault diagnosis in the field of AUV, the two kinds of methods, analytical model type and data-driven type, have achieved good performance and application. However, AUV dynamic model needs to be adjusted online in the analytical model type method, while the separation of weak fault feature and external disturbance required to further research in the data-driven type method. In the future research, the authors will establish development coefficient and grey action quantity based on grey prediction principal and optimization of grey derivative equations background value, adjust the prediction results based on prediction residual and fuse time-sequence prediction result, so as to predict dynamically the trend of weak thruster fault.

References

[1] HAMILTON K, LANE D M, BROWN K E, EVANS J, TAYLOR N K. An integrated diagnostic architecture for autonomous underwater vehicles [J]. Journal of Field Robotics, 2007, 24(6): 497-526.

[2] LI Juan, ZHOU Dong-hua, SI Xiao-sheng, CHEN Mao-yin, XU Chun-hong. Review of incipient fault diagnosis methods [J]. Control Theory & Applications, 2012, 29(12): 1517-1529. (in Chinese)

[3] EDIN O, GEOFF R. Thruster fault diagnosis and accommodation for open-frame underwater vehicles [J]. Control Engineering Practice, 2004, 12(12): 1575-1598.

[4] WANG Guo-biao, HE Zheng-jia, CHEN Xue-feng, LAI Yi-nan. Basic research on machinery fault diagnosis-what is the prescription [J]. Journal of Mechanical Engineering, 2013, 49(1): 63-72. (in Chinese)

[5] ZHOU Dong-hua, SHI Jian-tao, HE Xiao. Review of intermittent fault diagnosis techniques for dynamic systems [J]. Acta Automatica Sinica, 2014, 40(2): 161-171. (in Chinese)

[6] BIAN Xin-qian, MOU Chun-hui, YAN Zhe-ping, CHENG Xiang-qin. Reliability research of UUV based on fault tree [J]. Shipbuilding of China, 2011, 52(1): 71-79. (in Chinese)

[7] QIN Z, GU J. Sensor fault detection and identification based on gray model for autonomous underwater vehicle [J]. Mediterranean Jouranl of Measurement and Control, 2009, 5(2): 71-77.

[8] BO Z, ROGER S, MOGENS B, FREDRIK D. Particle filter for fault diagnosis and robust navigation of underwater robot [J]. IEEE Transactions on Control Systems Technology, 2014, 22(6): 2399- 2407.

[9] LIU Qian, ZHU Da-qi, SIMON X Y. Unmanned underwater vehicles fault identification and fault-tolerant control method based on FCA-CMAC neural networks, applied on an actuated vehicle [J]. J Intell Robot Syst, 2012, 66(1): 463-475.

[10] GAO Fu-dong, PAN Cun-yun, HAN Yan-yan, ZHANG Xiang. Nonlinear trajectory tracking control of a new autonomous underwater vehicle in complex sea conditions [J]. Journal of Central South University of Technology, 2012, 19(7): 1859-1868.

[11] ZHANG Li-jun, QI Xue, PANG Yong-jie. Adaptive output feedback control based on DRFNN for AUV [J]. Ocean Engineering, 2009, 36(3): 716-722.

[12] WANG Sheng-wu, SHI Xiu-hua, XU Hui, TANG Wan-wen. Fault diagnosis of UV’s sensors based on wavelet neural network [J]. Journal of Test and Measurement Technology, 2010, 24(4): 361-367.

[13] ZHANG Ming-jun, WU Juan, CHU Zhen-zhong. Multi-fault diagnosis for autonomous underwater vehicle based on fuzzy weighted support vector domain description [J]. China Ocean Engineering, 2014, 28(5): 1-18.

[14] ZHANG Ming-jun, LIU Wei-xin, YIN Bao-ji, WANG Yu-jia. Fault feature enhancement for autonomous underwater vehicles [J]. Journal of Harbin Engineering University, 2014, 35(9): 1099-1105. (in Chinese)

[15] LEI Ya-guo, HAN Dong, LIN Jing, HE Zheng-jia. Planetary gearbox fault diagnosis using an adaptive stochastic resonance method [J]. Mechanical Systems and Signal Processing, 2013, 38(1): 113-124.

[16] JIAO Shang-bin, LI Peng-hua, ZHANG Qing, HUANG Wei-chao. Multi-frequency weak signal detection method based on adaptive stochastic resonance with knowledge-based PSO [J]. Journal of Mechanical Engineering, 2014, 50(12): 1-10. (in Chinese)

[17] LENG Yong-gang, WANG Tai-yong, GUO Yan, WU Zhen-yong. Study of the property of the parameters of bistable stochastic resonance [J]. Acta Physica Sinica, 2007, 56(01): 30-35. (in Chinese)

[18] LI Ji-meng, CHEN Xue-feng, HE Zheng-jia. Adaptive stochastic resonance method for impact signal detection based on sliding window [J]. Mechanical Systems and Signal Processing, 2013, 36(2): 240-255.

[19] LI Qiang, WANG Tai-yong, LENG Yong-gang, WANG Wei, WANG Guo-feng. Engineering signal processing based on adaptive step-changed stochastic resonance [J]. Mechanical Systems and Signal Processing, 2007, 21(5): 2267-2279.

[20] YI Qin, YI Tao, YE He, TANG Bao-ping. Adaptive bistable stochastic resonance and its application in mechanical fault feature extraction [J]. Journal of Sound and Vibration, 2014, 333(26): 7386-7400.

[21] ADAM P P, JAROSLAW J N, PAWEL M R. How novel is the “novel” black hole optimization approach [J]. Information Sciences, 2014, 267: 191-200.

[22] LI Jun-jun, HUANG You-fang, YANG Bin. Alternately preying particle swarm optimization algorithm and convergence analysis of its particle trajectories [J]. Control Theory & Applications, 2013, 30(7): 850-855. (in Chinese)

[23] ZHANG Ming-jun, WU Juan, WANG Yu-jia. A method of multi-sensor simultaneous faults detection for autonomous underwater vehicle [J]. Robot, 2010, 32(3): 298-305. (in Chinese)

[24] WANG Shi-bin, CAI Gai-gai, ZHU Zhong-kui, HUANG Wei-guo, ZHANG Xing-wu. Transient signal analysis based on Levenberg-Marquardt method for fault feature extraction of rotating machines [J]. Mechanical Systems and Signal Processing, 2015, 54-55: 16-40.

[25] TANG Bao-ping, LIU Wen-yi, SONG Tao. Wind turbine fault diagnosis based on morlet wavelet transformation and Wigner-Ville distribution [J]. Renewable Energy, 25(12): 2862-2866.

[26] WANG Li-rong, XU Yu-ru. Sensor fault diagnosis of autonomous underwater vehicle [J]. Robot, 2006, 28(1): 25-29. (in Chinese)

[27] TOMASZ B, ADAM J. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kutogram [J]. Mechanical Systems and Signal Processing, 20011, 25(1): 431-451.

[28] ZHANG Ming-jun, YIN Bao-ji, LIU Wei-xin, WANG Yu-jia. Feature extraction and fusion for thruster faults of AUV with random disturbance [J]. Journal of Huazhong University of Science & Technology: Natural Science Edition, 2015, 43(6): 22-26. (in Chinese)

(Edited by YANG Hua)

Foundation item: Project(51279040) supported by the National Natural Science Foundation of China

Received date: 2015-08-08; Accepted date: 2015-11-15

Corresponding author: WANG Yu-jia, Professor; Tel: +86-451-82519709; E-mail: wangyujia_1978@163.com