
J. Cent. South Univ. (2019) 26: 1886-1896
DOI: https://doi.org/10.1007/s11771-019-4142-3
Genetic algorithm and particle swarm optimization tuned fuzzy PID controller on direct torque control of dual star induction motor
BOUKHALFA Ghoulemallah1, BELKACEM Sebti1, CHIKHI Abdesselem2, BENAGGOUNE Said1
1. Faculty of Technology, Department of Electrical Engineering, University of Batna, Algeria;
2. Department of Science and Technology, Faculty of Technology, University of Batna, Algeria
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: This study presents analysis, control and comparison of three hybrid approaches for the direct torque control (DTC) of the dual star induction motor (DSIM) drive. Its objective consists of combining three different heuristic optimization techniques including PID-PSO, Fuzzy-PSO and GA-PSO to improve the DSIM speed controlled loop behavior. The GA and PSO algorithms are developed and implemented into MATLAB. As a result, fuzzy-PSO is the most appropriate scheme. The main performance of fuzzy-PSO is reducing high torque ripples, improving rise time and avoiding disturbances that affect the drive performance.
Key words: dual star induction motor drive; direct torque control; particle swarm optimization (PSO); fuzzy logic control; genetic algorithms
Cite this article as: BOUKHALFA Ghoulemallah, BELKACEM Sebti, CHIKHI Abdesselem, BENAGGOUNE Said. Genetic algorithm and particle swarm optimization tuned fuzzy PID controller on direct torque control of dual star induction motor [J]. Journal of Central South University, 2019, 26(7): 1886-1896. DOI: https://doi.org/10.1007/s11771- 019-4142-3.
1 Introduction
Nowadays, many actuators combining AC machines and static converters are showing new perspectives in the field of variable speed drive. Multiphase induction motors especially the dual star induction types are mostly used in advanced power applications [1-4]. The main superiority of these kinds of motors is [5]: higher efficiency and lower torque pulses. Vector control of the dual star induction motor (DSIM) is based on effective control of the magnetic state. However, this structure requires, in general, the installation of sensor on the shaft for the knowledge of a mechanical quantity. In addition, it remains very sensitive to machine parameters variations. However, the search for other algorithms has not ceased since and new control techniques have emerged [6-12].
Most current engineering control applications using proportional integral derivative (PID) control systems provide simpler and more efficient solutions. However, to meet the requirements of a variable speed drive, the PID controllers are poorly tuned.
Many tuning methods have been presented to remedy these problems. One of these proposed settings is the auto-adjustment of the PID controllers [13-15].
The arrival of heuristics and meta-heuristics has improved and facilitated the resolution of previously difficult or impossible to solve optimization problems [16-21]. Their general principle is to model the notions of evolution in nature as algorithms imitating natural evolution. Among them and recently, differential evolution (DE) [22], bat algorithm (BA) [23], CACO algorithm [24], hybrid GA [25], PSO [26], ant colony optimization (ACO) [27], bee colony algorithm (BC) [28, 29], imperialist competitive algorithm (IC) [30], hybrid PSO-GA [31, 32]. These methods have emerged as promising ones because of their ability to optimize in complex multimodal search spaces applied to non-differentiable functions.
The PSO is an evolutionary algorithm inspired by the social interaction of animals in nature. The particles, to evolve, are based on the imitation of the behavior of the best neighbor. Each particle is characterized by a position and speed. His experience is considered when updating his speed. Several approaches of PSO have been suggested in the literature [33]. For all these studies, the shared common feature is to avoid premature convergence to local optima.
Genetic a lgorithms (GAs) are an optimization technique that analyzes a vast research space and leads to more than one solution to the problem. In accordance with biological systems, the algorithms are based on genetic operators whose reproduction and mating lead to evolution. However, mutations explore the entire research space while avoiding premature convergence [34]. The result of the application of these three basic operations leads to the creation of new individuals whose qualities are better than their parent’s ones, and after several operations, the algorithm stops after it has reached an optimal solution.
In the past years, the fuzzy logic controller (FLC) has improved successfully as a result of complex and non-linear processes [35-37]. The design of an FLC has two disadvantages. The first is the difficulty of regulating the appropriate bases, while the second consists in selecting scale factors before to be fuzzified and after defuzzified. To overcome them, we use optimization methods to determine the gains of the fuzzy logic.
The major contribution of this work is to compare three approaches based on the meta- heuristic DTC optimization technique of the DSIM. The first technique uses the merits of PSO to judiciously adjust the scale factors of the PID, the second one associates fuzzy control as a constraint for an efficient optimization solution based on a PSO algorithm and the latest strategy combines genetic algorithms with fuzzy control for their optimization. It allows a judicious choice of a relative scaling factor for the PID controller of the DSIM.
2 Dynamic behavior of DSIM
The DSIM dynamics model is written as follows [5]:
 (1)
(1)
where the fluxes expressions are:
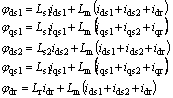
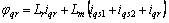 (2)
(2)
The rotor speed formulation ispresented as follows:
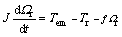 (3)
(3)
The explanation of the torque Tem given below [3]:
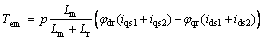 (4)
(4)
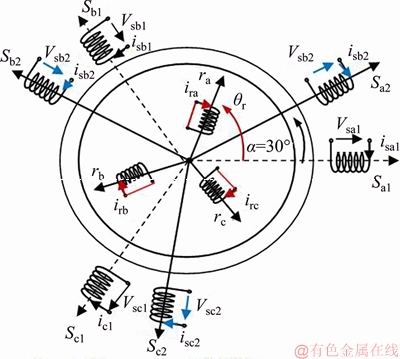
Figure 1 Windings diagram of DISM
3 Traditional DTC of DSIM
To overcome the problems of sensitivity to parametric variations, many control methods have been developed in which the stator flux and the electromagnetic torque are estimated from the only electrical quantities accessible to the stator, without recourse to mechanical sensors [38].
Direct torque control (DTC), based on the stator flux orientation, is one of the methods introduced by TAKAHASHI et al [38]. This type of control has been presented as an alternative to vector control by rotor flux orientation (RFO), which has the major disadvantage of being relatively sensitive to the machine parameters variations. DTC is created by this algorithm:
At each sampling instant, partition the complex plan into short time periods;
Measure the phase voltages and line currents for each time;
Estimate the electromagnetic torque, stator flux and the measurement line currents;
Introduce the difference between the reference torque and the estimated torque in a three-level hysteresis regulator, which gives the value +1 to increase the flux, -1 for reduce it and 0 to keep it constant. This choice increasing the number of levels, and this advantage reduces the switching frequency, since the dynamics of the torque is generally faster than that of the flux;
Using the switching table, the operating sequences of the drive are determined;
The division of the complex plane into six angular sectors makes it possible to determine, for each given sector, the control sequence of the switches of the inverter corresponds to different states of the variables control and according to the logic of the flux control and the torque with respect to the application of a stator voltage vector.
Figure 2 shows the illustrative block of the classical DTC of DSIM.
4 Presentation of PSO technique
Meta-heuristics are optimization methods to obtain an approximate value of the optimal solution in a reasonable time. They have objective for the resolution of a set of problems in different fields without having to modify the basic algorithm of the principle method. A particular interest is brought to the approach of optimization PSO. It is based on the “social interactions” between “agents” called “particles”, in order to achieve a given goal in a common research space where each particle has a certain capacity for memorizing and processing information. This stochastic meta-heuristic optimization was proposed in by EBERHART et al [19].
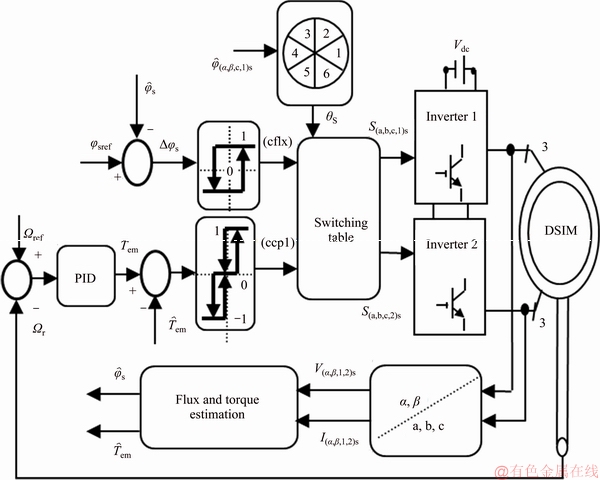
Figure 2 Classical DTC of dual star induction motor drive
Knowing that the swarm has a dimension n, that the research space is m, and since the place of the ith particle is disposed as xi=(xi1, xi2, …, xd). The best earlier locations of the ith particle are considered by EBERHART et al [19].
pbesti=(pbesti1, pbesti2, …, pbestid) (5)
The most interesting agent of the group is gbestd and its speed is given by:
vi=(vi1, vi2, …, vid) (6)
The speed and position of each agent undergoing change can be determined with the aid of the current and the distance of pbestid, shown on Eqs. (7) and (8) [31]:
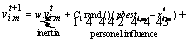
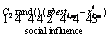 (7)
(7)
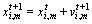 i=1, 2, …, n, m=1, 2, …, d (8)
i=1, 2, …, n, m=1, 2, …, d (8)
4.1 Basic steps of PSO
The different steps of the PSO algorithm are established as follows.
First step: We define the values of the inertia factor w with C1=C2 representing the constants of the PSO algorithm which must optimize the three main scaling factors of the fuzzy regulator, deduced from the optimal value of the swarm research.
Second step: We have randomly chosen a search space of “50” agents by adopting (xi1, xi2, xi3), (vi1, vi2, vi3) as the first prediction of the speed, to reach the optimal function pbest1.
Third step: Perform the PSO algorithm with n iterations, to find the best “gbest” position of the fitness function. Table 1 displays the parameters of the PSO.
Updated speed and position are illustrated in Figure 3.
The flowchart of the fuzzy PSO-DTC-DSIM is shown schematically in Figure 4.
Table 1 Simulation parameters of PSO algorithm

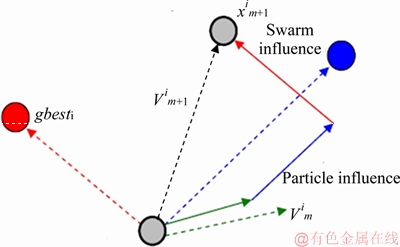
Figure 3 Representation of PSO algorithm

Figure 4 Organigram for fuzzy PSO based DTC
4.2 Performance of fitness function
The IAE criterion is widely used to evaluate the performance of the system [21]:
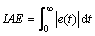 (9)
(9)
5 GA-based fuzzy-PID controller tuning
Heuristic optimization proposes a hybrid approach integrating the merits of two techniques, the FLC and the GA. GAs is an optimization approach using the basis of genetics and the principles of natural evolution: crosses, mutations, selections, etc, GAs is finest suited for complicated problems. Moreover, every agent is evaluated according to its fitness to contribute the objective function. The GA parameters are described in Table 2.
Figure 5 shows the flowchart for fuzzy GA-DTC-DSIM.
Table 2 GA setup parameters



 Figure 5 Organigram for fuzzy GA-DTC-DSIM
Figure 5 Organigram for fuzzy GA-DTC-DSIM
6 Hybrid PID-PSO type FLC
The determination of the scaling factors of the FLC by PSO algorithm is presented respectively by the input and output as {e}, and {ec} as given bellow:
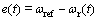 (10)
(10)
 (11)
(11)
Table 3 depicts the optimized PID controller by PSO algorithm.
Table 3 Results of PID controller optimized by PSO

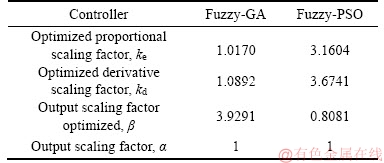
When using fuzzy logic in a PID controller, emphasis is placed on fuzzy proportional integral action (F-PI) despite its unsatisfactory response during the transient regime. However, the action fuzzy proportional derivative (F-PD) cannot ensure a reliable steady state. Therefore, the combination of F-PI and F-PD is more convenient to create a regulator F-PID in order to obtain PID action of the regulator. It is essential to control F-PID by adding the output of the fuzzy PD controller and its integral part whose model is shown in Figure 6 and the scale factors are shown in Table 4.
The output u of the fuzzy regulator is illustrated by:
 (12)
(12)
The value of the output according to the input is illustrated in Eq. (13):

Figure 6 Fuzzy speed controller structure associated with PSO or GA
Table 4 Results of optimization by fuzzy regulator
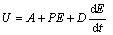 (13)
(13)
Thus, combining Eqs. (12) and (13), the output of the controller is obtained as follows:
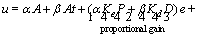
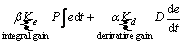 (14)
(14)
6.1 Fuzzification
During the fuzzification interface, we defined the triangular membership functions forms for the output and input variables (e, ec, dTem) as represented in Figures 7 and 8 for the proposed regulator. However, the transition from these physical quantities to linguistic variables (NL, NM, NS, ZE, PS, PM, PL) can be treated by inference rules.
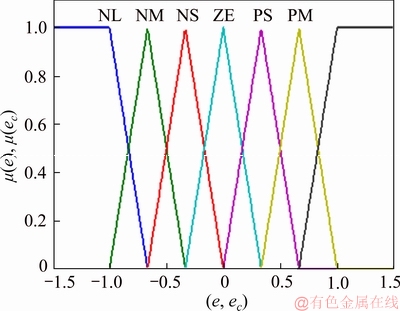
Figure 7 Seven appurtenance functions of input error and derivative error
6.2 Inference and defuzzification
Defuzzification using the MIN manner to obtain the degree μ (dTem) relative to each inference rule, so we write 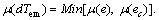
During defuzzification, a value of torque is obtained by the output function as:
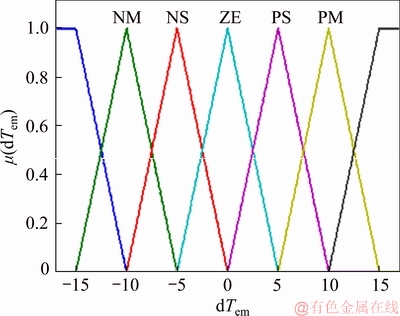
Figure 8 Seven appurtenance functions of output dTem
 (15)
(15)
6.3 Rules of inference
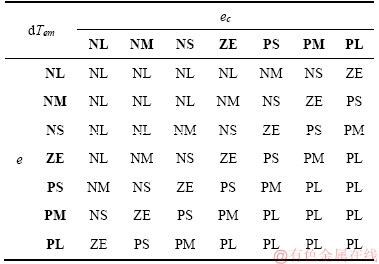
The fuzzy rule table represents the heart of the system and combines these rules to describe the behavior of the system:
If e is PL and ec is PL then dTem is PL.
We notice that the difference is very important between the speed response and its reference (e is PL), so we must reinforce the gain (dTem is PL) so that the speed reaches its reference. The inference rules are given in Table 5.
Table 5 Inference rules
7 Simulation and analysis
To have a more appreciation of the results obtained through the different approaches PID-PSO, fuzzy-PSO and fuzzy-GA, it is necessary to make a comparison of the static and dynamic characteristics of the three control techniques under the same operating conditions (references, disturbance loads, …) and in the same simulation configuration, then make a choice of the type of control according to the desired application. We performed a simulation under MATLAB/ SIMULINK environment. Table 6 gives the rated values of the DSIM. The scheme of the simulated techniques is illustrated in Figure 9. The simulation results obtained are given through the following figures.
Table 6 DSIM parameters[5]
In Figure 10, the speeds controlled by the three controllers are presented. When the DSIM is operated at 100 rad/s under a load torque of 14 N·m at t=0.6 s. We can view that the use of fuzzy-PSO controller gives good performances, very rapid rejection of the applied load torque, small settling time, without overshoot and with reduced steady state error, contrary to a Fuzzy-GA controller where the speed has suffered a slight rejection which is more visible with a hybrid controller PID-PSO.
For a more comprehensive analysis, one compares through Table 7 the results obtained for the different controllers according to the different errors ISE (integral squared error), integral absolute error (IAE) and integral time squared error (ITSE). We conclude that the fuzzy-PSO approach provides good performance.
Figure 11 illustrates the electromagnetic torque response of the DSIM by the proposed three methods. The technical DTC-PID suffers from two major drawbacks which are the static error and exaggerated fluctuations. Though, Fuzzy-PSO brings the necessary correction to the operation of the system. Nevertheless, the fuzzy-GA is less satisfactory.
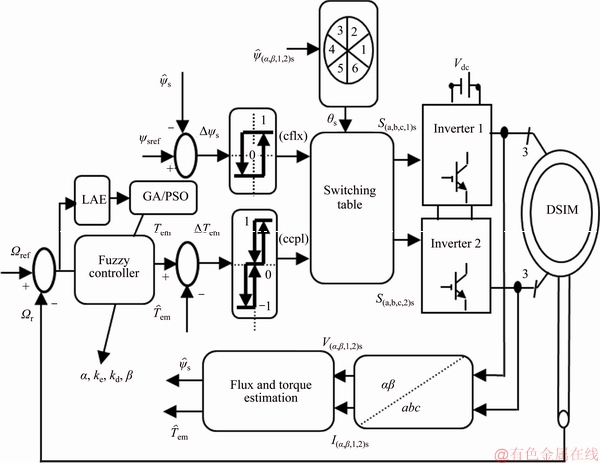
Figure 9 Illustrative diagram of proposed GA or PSO based DTC for speed controller of DSIM
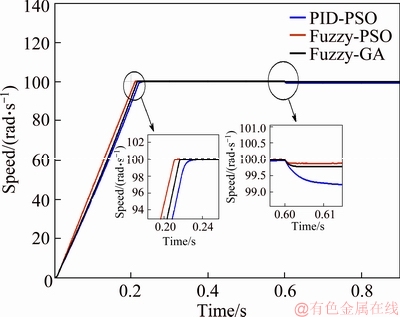
Figure 10 Simulation results for speed regulation of three controllers
Table 7 Performance comparison of three controllers

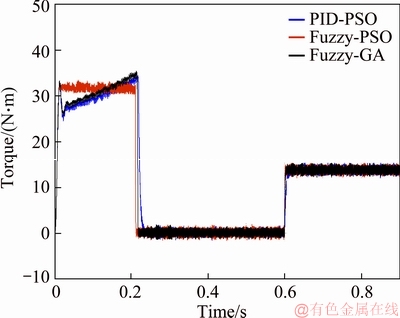
Figure 11 Comparison of torque results for proposed three approaches
Figure 12 illustrates the sinusoidal shape of the currents and the important role played by the fuzzy-PSO by significantly reducing the current ripple relative to the other controllers. The results reveal that the fuzzy-PSO algorithm is best suited for PID gaintuning.
We notice that the stator flux trajectories for the three controllers shown in the Figure 13 are superimposed, however, the blurred PSO shows less fluctuations.
The variation of the speed error (fitness) is summarized in Figures 14 and 15.It is worthy to mention that, fuzzy-PSO method outperforms fuzzy-GA method (see Table 7).
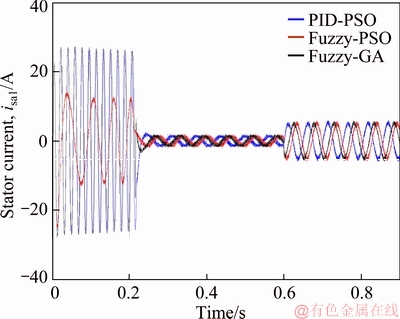
Figure 12 Phase current in stator winding (1) of three controllers
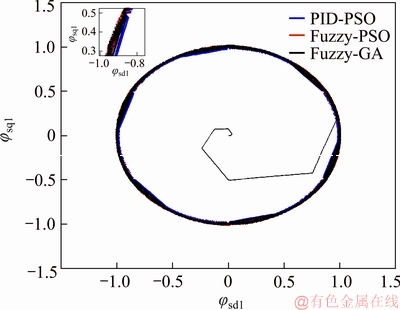
Figure 13 Stator flux trajectory in stator (1) of three controllers
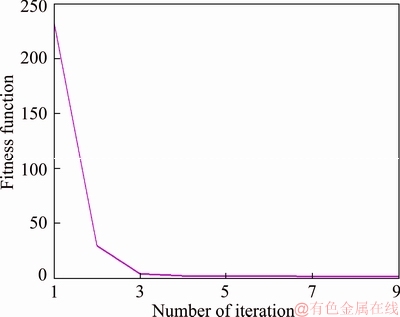
Figure 14 Speed error (fitness function) of fuzzy-GA (Table 4)
8 Conclusions
In this study, we have presented a strategy for optimizing the operation of direct torque control of the DSIM. The latter is based on the substitution of the classical PID speed controller by different recent heuristic optimization techniques which are the association of fuzzy logic with genetic algorithms fuzzy-GA and the combination of fuzzy logic with particle swarm optimization fuzzy-PSO. The most efficient training of our system was obtained according to the results of simulations with the conjunction of fuzzy logic with particle swarm optimization regulator. Indeed, the latter has shown its ability to significantly reduce torque ripples and provide drive by eliminating the steady state error.
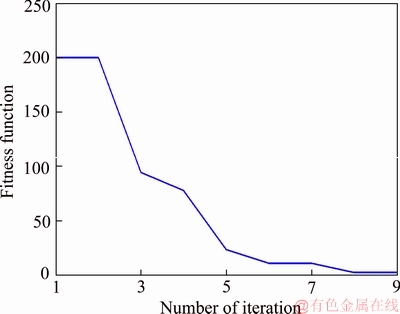
Figure 15 Speed error (fitness function) of Fuzzy-PSO (Table 3)
Nomenclature
Vds1, Vqs1, Vds2,Vqs2
Statorique voltages
Ids1, Iqs1, Ids2, Iqs2
Statoriquecurrents
Idr, Iqr
Rotoriquecurrents
φds1, φqs1, φds2
Stator flux vectors
φdr, φqr
Rotor fluxes
Tem
Electromagnetic moment
Tr
Torque load
Ωr
Mechanical speed
ωr
Rotor angular speed
ωs
Stator angular speed
n
Number of particles
d
Dimension indices
vti,m
Speed of particle
w
Weight factor ofinertia
rand ()
Random number
pbesti
Best previous position
gbest
Best particle
C1, C2
Acceleration constant
NL
Negative large
NM
Negative medium
NS
Negative small
ZE
Zero equal
PS
Positive small
PM
Positive medium
PL
Positive large
ISE
Integral squared error
IAE
Integral absolute Error
ITSE
Integral time squared error
PID
Proportional integral derivative
FLC
Fuzzy logic control
References
[1] ZHAO Y, LIPO T A. Space vector PWM control of dual three-phase induction machine using vector space decomposition [J]. IEEE Trans Ind Appl, 1995, 31(5): 1100-1108. DOI: 10.1109/28.464525.
[2] HADIOUCHE D, RAZIK H, REZOUG A. On the modeling and design of dual-stator windings to minimize circulating harmonic currents for VSI fed AC machines [J]. IEEE Trans on Industry Applications, 2004, 40(2): 506–515. DOI: 10.1109/TIA.2004.82451.
[3] CHE H S, LEVI E, JONES M, DURAN M J, HEW W P, RAHIM N A. Operation of six-phase induction machine using series-connected machine-side converters [J]. IEEE Trans Ind Electron, 2015, 61(1): 164–176. DOI: 10.1109/TIE. 2013.2248338.
[4] OJO O, WU Z. Speed control of a dual stator winding induction machine [J]. APEC second Annual IEEE Applied Power Electronics Conference and Exposition, 2007: 229-235. DOI: 10.1109/APEX.2007.357519.
[5] OUDJEBOUR Z, BERKOUK E M, MAHMOUDI M O. Stabilization by new control technique of the input DC voltages of five-level diode-Clamped inverters. Application to double star induction machine [C]// 2nd International Symposium on Environment Friendly Energies and Applications. Newcastle: IEEE, 2012: 541-544 DOI: 10.1109/EFEA.2012. 6294034.
[6] LAZREG M H, BENTAALLAH A. Speed sensorless vector control of double star induction machine using reduced order observer and MRAS estimator [C]// 6th International Conference on Electrical Engineering (ICEE). Boumerdes, Algeria: ICEE, 2017: 111-118. DOI: 10.1109/ICEE-B.2017.8192150.
[7] YOUBL, BELKACEM S, NACERI F, CERNAT M, PESQUER L G, Design of an adaptive fuzzy control system for dual star induction motor drives [J]. Advances in Electrical and Computer Engineering, 2018, 18(3): 37-44. DOI: 10.4316/AECE.2018.03006.
[8] LAAMAYAD T, NACERI F, BELKACEM S. A fuzzy sliding mode strategy for control of the dual star induction machine [J]. Journal of Electrical Engineering, 2013, 13(3): 216-223. http://www.jee.ro/covers/art.php? Issue=WH13418 36520.
[9] VEGA P, PRADA C, ALEIXANDER V. Self-tuning predictive PID controller [J]. IEE Proc, 1991, 138(3): 303-311. DOI: 10.1049/ip-d.1991.0041.
[10] KRZYSZTOF P. Analysis and control of dual stator winding induction motor [J]. Archives of Electrical Engineering, 2012, 61(3): 421-438. DOI: 10.2478/v10171-012-0033-z.
[11] MINOUNI M F, DHIFAOUI R. Speed identification for deadbeat rotor flux level control of double-star induction machine [C]// IEEE International Conference on Systems, Man and Cybernetics. Hammamet, Tunisia: IEEE, 2002: 712-718. DOI: 10.1109/ICSMC.1176322.
[12] BENCHOUIA M T, GHADBANE I, GOLEA A, SRAIRI K, BENBOUZID M H. Implementation of adaptive fuzzy logic and PI controllers to regulate the DC bus voltage of shunt active power filter [J]. Appl Soft Comput, 2015: 125-131. https://doi.org/10.1016/j.asoc.2014.10.043.
[13] SWAGAT P, KANUNGO B M, DEBIPRASANNA D. A hybrid self-tuned fuzzy controller for indirect vector controlled induction generator [C]// India Conference (INDICON), 2012 Annual IEEE. India: IEEE, 2012: 614-619. DOI: 10.1109/.2012.6420660.
[14] MASIALA M, VAFAKHAH B, SALMON J, KNIGHT A. Fuzzy self-tuning speed control of an indirect field-oriented control induction motor drive [C]// Proceedings of IEEE Indapplsocann Meet. USA: IEEE, 2007: 614-619. DOI: 10.1109/07IAS. 2007.156.
[15] QIAO W Z, MIZUMOTO M. PID type fuzzy controller and parameters adaptive method [J]. Fuzzy Sets and Systems, 1996, 78(2): 23-35. DOI: 10.1016/0165-0114(95) 00115-8.
[16] WU D, HUIMIN Z, LI Z, GUANGYU L, XINHUA Y, DAQING W. A novel collaborative optimization algorithm in solving complex optimization problems [J]. Soft computing, 2017, 21(15): 4387-4398. DOI: 10.1007/s00500-016- 2071-8.
[17] QIAO W, VENAYAGAMOORTHY G K, HARLEY R G. Design of optimal pi controllers for doubly fed induction generators driven by wind turbines using particle swarm optimization [C]// Proceedings of the IEEE International Joint Conference on Neural Network. Canada: IEEE, 2006: 1112-1117. DOI: org/10.1109/IJCNN.2006. 246944.
[18] ZHONG F, LI H, ZHONG S. An improved artificial bee colony algorithm with modified-neighborhood-based update operator and independent-inheriting-search strategy for global optimization [J]. Eng Appl Artif Intell, 2017, 58: 134-156. DOI: 10.1016/j.engappai.2016.11.005.
[19] EBERHART R, KENNEDY J. A new optimizer using particles warm theory [C]// Proceedings of the Sixth International Symposium on Micro Machine and Human Science. Japan, 1995: 39-43. DOI: 10.1109/MHS.1995. 494215.
[20] BOUKHALFA G, BELKACEM S, CHIKHI A, BENAGGOUNE S. Direct torque control of dual star induction motor using a fuzzy-PSO hybrid approach [J]. Applied Computing and Informatics, 2018, DOI: 10.1016/ j.aci.2018.09.001.
[21] XUEWEN X, YING X, BO W, YINGLONG Z, XIONG L, XIANLI D, LING G. A fitness-based multi-role particle swarm optimization [J]. Swarm and Evolutionary Computation, 2018, 44(1): 349-364. DOI: org/10.1016/ j.swevo.2018.04.006.
[22] BHARTI O P, SAKET R K, NAGAR S K. Controller design of DFIG based wind turbine by using evolutionary soft computational techniques [J]. Engineering, Technology & Applied Science Research, 2017, 7(3): 1732-1736. https://www.etasr. com/index.php/article/view/1231.
[23] PREMKUMAR K, MANIKANDAN B. Speed control of brushless DC motor using bat algorithm optimized adaptive neuro-fuzzy inference system [J]. Applied Soft Computing, 2015, 32(2): 403-419. DOI: 10.1007/s00170-016-9092-4.
[24] DENG Wu, ZHAO Hui-min, LIU Jing-jing, YAN Xiao-lin, LI Yuan-yuan, YIN Li-feng, DING Chuan-hua. An improved CACO algorithm based on adaptive method and multi- variant strategies [J]. Soft Computing, 2015, 19(3): 701-713.DOI:10.107/s050-014-1294-9.
[25] WIBOWO W K, JEONG S. Genetic algorithm tuned PI controller on PMSM simplified vector control [J]. Journal Central South University, 2013, 20: 3042-3048. DOI: 10.1007/ s11771-013-1827-x.
[26] JOHN A. RAMIREZ, JES S M. L
S M. L PEZ, LEZAMAAND N Mu
PEZ, LEZAMAAND N Mu oz G. Particle swarm metaheuristic applied to the optimization of a PID controller [J]. Contemporary Engineering Sciences, 2018, 11(67): 3333-3342. DOI: org/ 10.12988/ces.2018.873.
oz G. Particle swarm metaheuristic applied to the optimization of a PID controller [J]. Contemporary Engineering Sciences, 2018, 11(67): 3333-3342. DOI: org/ 10.12988/ces.2018.873.
[27] JASDEEP K, SHEELA T. Performance comparison of variants of ant colony optimization technique for online tuning of a PI controller for a three phase induction motor drive [J]. International Journal of Computer Science Information Technologies, 2014, 5(4): 5814-5820. http://www.ijcsit.com//Volume%205/vol5issue04/ijcsit201405216.pdf.
[28] ZHANG Mei, TAN Ying-tong, ZHU Jin-hui, CHEN Yi-nong, LIU Hai-ming. Modeling and simulation of improved artificial bee colony algorithm with data-driven optimization [J]. Simulation Modelling Practice and Theory, 2019, 93: 305-321. DOI: 10.1016/j.simpat.2018.06.004.
[29] GAO W F, HUANG L L, WANG J, LIU S Y, QIN C D. Enhanced artificial bee colony algorithm through differential evolution [J]. Appl Soft Comput, 2016, 48: 137-150. DOI: 10.1016/j.asoc.2015.10.070.
[30] EHAB S A. Imperialist competitive algorithm for optimal STATCOM design in a multimachine power system [J]. International Journal of Electrical Power & Energy Systems, 2015, 76(3), DOI: org/10.1016/j.ijeps.2015.09.004.
[31] GARG H. A hybrid PSO-GA algorithm for constrained optimization problems [J]. Applied Mathematics and Computation, 2016, 274(2): 1292-1305.
[32] GACEM A, BENATTOUS D. A hybrid genetic algorithm and particle swarm optimization for multimodal functions [J]. Applied Soft Computing, 2008, 8(2): 849-857. DOI: org/10.1016/ j.asoc.2007.07.002.
[33] MESLOUB H, BENCHOUIA M T, BOUMAARAF R, GOLEA A, GOLEA N, BECHERIF M. Design and implementation of DTC based on AFLC and PSO of a P MSM [J]. Mathematics and Computers in Simulation, 2018, DOI: org/10.1016/ j. matcom.2018.04.010.
[34] GOLDBERG D E. Genetic algorithm in search optimization and machine learning [M]. MA: Addison-Wesley, 1989. https://dl.acm.org/citation.cfm?id=534133.
[35] TIR Z, MALIK O P, ELTAMALY A M. Fuzzy logic based speed control of indirect field oriented controlled double star induction motors connected in parallel to a single six-phase inverter [J]. Electric Power Systems Research, 2016, 134(2): 126-133. https://doi.org/10.1016/j.epsr.2016.01.013.
[36] GUZELKAYA M, EKSIN I, YESIL E. Self-tuning of PID-type fuzzy logic controller coefficients via relative rate observer [J]. Engineering Applications of Artificial Intelligence, 2003, 16: 227-236. DOI: https://doi.org/10. 1016/S0952-1976(03)00050-2.
[37] LEKHCHINE S, BAHI T, SOUFI Y. Indirect rotor field oriented control based on fuzzy logic controlled double star induction machine [J]. Electrical Power and Energy Systems, 2014, 57: 206-211.
[38] TAKAHASHI I, NOGUCHI T. A new quick-response and high-efficiency control strategy of an induction motor [J]. IEEE Transactions on Industry Applications, 1986, 22(5): 820-827. DOI: 10.1109/TIA.1986.4504799.4ffacce8340e7.
(Edited by HE Yun-bin)
中文导读
基于遗传算法和粒子群优化的模糊PID控制器在双星感应电机直接转矩控制中的应用
摘要:本文对双星感应电动机直接转矩控制的三种混合方法进行了分析、控制和比较,目的是将PID-PSO、模糊PSO和GA-PSO三种不同的启发式优化技术相结合,以改善DSIM速度控制回路的性能。将遗传算法和粒子群优化算法应用于MATLAB,得到模糊粒子群算法是最合适的方案。模糊粒子群算法的主要性能是减小了大扭矩波动,加快了上升时间,避免了影响驱动性能的干扰。
关键词:双星感应电机驱动;直接转矩控制;粒子群优化(PSO);模糊逻辑控制;遗传算法
Foundation item: Project supported by Faculty of Technology, Department of Electrical Engineering, University of Batna, Algeria
Received date: 2018-02-14; Accepted date: 2018-10-31
Corresponding author: BOUKHALFA Ghoulemallah, PhD Candidate; Tel: +213-66-8888620; E-mail: ghoulem1987@gmail.com; ORCID: 0000-0002-9427-9983