J. Cent. South Univ. (2017) 24: 1992-2000

DOI: https://doi.org/10.1007/s11771-017-3608-4

Integral sliding mode control for flexible ball screw drives with matched and mismatched uncertainties and disturbances

BAO Da-fei(包达飞), TANG Wen-cheng(汤文成), DONG Liang(董亮)

School of Mechanical Engineering, Southeast University, Nanjing 211189, China

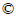Central South University Press and Springer-Verlag GmbH Germany 2017

Abstract: The design of servo controllers for flexible ball screw drives with matched and mismatched disturbances and uncertainties is focused to improve the tracking performance and bandwidth of ball screw drives. A two degrees of freedom mass model is established based on the axial vibration characteristics of the transport ball screw, and the controller of an adaptive integral sliding mode is proposed combining the optimal design of state feedback gain matrix K to restrain the vibration and the matched disturbances and uncertainties. Then for the counteraction of the mismatched disturbances and uncertainties, a nonlinear disturbance observer is also developed. The trajectory tracking performance experiments and bandwidth analysis were conducted on experimental setup with the proposed control method. It is proved that the adaptive integral sliding mode controller has a high tracking performance and bandwidth especially for the axial vibration characteristics model of ball screw drives. And the ball screw tracking accuracy also has a considerable improvement with the application of the proposed nonlinear disturbance observer.

Key words: ball screw drives; matched and mismatched disturbances and uncertainties; axial vibration characteristics; adaptive integral sliding mode control; nonlinear disturbance observer

1 Introduction

Ball screw drives are widely used in the machine tool feed systems for its outstanding advantages like high stiffness, accuracy and transmission efficiency [1]. As the requirements of CNC (computer numerical control) machine tools used in aviation industry, automobile industry and mould manufacturing are increasing, higher performance of linear motion elements like ball screw drives is needed under higher speed operating condition. Normally, the ball screw drive model is equivalent to the rigid model. However, it is supposed that the torsional and axial vibration modes can be excited under the fast movements of high acceleration, which can produce structural vibrations [2]. Structural vibrations are the definitive factors which can limit the achievable bandwidth and deteriorate the accuracy performance of tracking and positioning in the transport system [3]. In addition, the parametric uncertainties and external disturbances encountered in the real system also act on an important obstacle for high positioning and tracking performance [4]. The system uncertainties are mainly incited by the table position variations and structural flexibility [5]. Furthermore, the external disturbances are dominant with the nonlinear friction and cutting force [6]. Combined with the above viewpoints, a relatively comprehensive consideration is required to achieve the high bandwidth and tracking performance.

The demand of a high precision control cannot be satisfied with classical controllers due to the structural vibration, external disturbances and parametric uncertainties of ball screw drives [7]. As the result, a significant amount of new control techniques have been researched in recent years, dedicated to developing faster and higher tracking performance ball screw drive systems [8, 9]. LEE et al [10] proposed a semi- continuous sliding mode controller which contained friction compensator especially for rigid model to reduce chatter characteristics of ball screw system. A sliding mode controller for ball screw drives was proposed by ALTINTAS et al [11] for the rigid model dynamics, and a notch filter was used to filter out the first order vibration. Combined with pole placement principle, ERKORKMAZ et al [12] further designed a controller based on adaptive sliding mode controller of the axial vibrations, which had a substantial improvement both in the bandwidth and tracking performance. Based on the study of ERKORKMAZ et al [12], OKWUDIRE and ALTINTAS [13] proposed a discrete-time sliding mode controller of ball screw assembly aimed at structural flexibility. GORDON and ERKORKMAZ [14] used the technique of pole-placement to compensate the active structural vibrations and then achieved the high bandwidth interference reduction and high positioning accuracy of the ball screw drives, which obtained a much more intuitive and simple effect on parameter adjustment. However, some significant factors like the external disturbances and the time varying parametric uncertainties were ignored in the mentioned articles. And then DONG and TANG [15] noticed that and proposed an adaptive backstepping sliding mode controller for the flexible ball screw drive systems considering time- varying uncertainties and external disturbances, which improved the tracking accuracy obviously. The dynamic variations caused by table position, mass change and the mechanical flexibility were taken into account by SEPASI et al [5] who designed a robust gain scheduling controller with table position scheduling. For the flexible ball screws, HANIFZADEGAN and NAGAMUNE [16] recently proposed a switching gain-scheduled controller [17] with an extensive range of application by using analytical LPV (linear parameter-varying) model of the flexible ball screws. LIAO et al [18] proposed a backstepping adaptive dynamic sliding mode controller to improve the trajectory tracking performance of the underactuated unmanned surface vehicles.

In this work, the first main contribution is the compensation of the axial vibration. A two-degree freedom model is taken to capture the first axial mode of the ball screw drive system. The ball screw drive is a various system with matched and mismatched disturbances and uncertainties since the external disturbances and time-varying uncertainties. To counteract the influence of the disturbances and uncertainties, an AISMC (adaptive integral sliding mode controller) with NDO (nonlinear disturbance observer) is adopted in this work for the flexible ball screw drive. The experiments were conducted to verify the effectiveness of the overall control strategy in comparison with a P-PI (proportional-proportional integral) controller.

2 Mathematical model of flexible ball screw drive

The ball screw drive experimental setup is shown in Fig. 1. The table is driven by a high-precision ball screw of 20 mm pitch and 20 mm diameter and supported on precision linear guideways on the both sides. The experimental setup is powered by a 9 kW synchronous AC servomotor connected to one end of the ball screw with a coupling. In addition, the end closed to the motor is fixed-end; the other end is supported-end. Two incremental rotary encoders are installed on the both sides of the ball screw and an incremental linear encoder is installed on the table. These devices are used to feedback position and velocity signals. And the setup is controlled by a dSPACE control system with a sampling frequency of 1.65 MHz.

Fig. 1 Ball screw drive experimental setup

To identify the first axial-vibration mode of the ball screw drive experimental setup, the open loop frequency response functions (FRFs) with input command voltage to the motor and the output displacement of table were measured in three different positions, as shown in Fig. 2. A sine sweep signal in range of 10-400 Hz was generated as the input signal. According to the figure, the first axial-vibration mode is about 100 Hz, and the first vibration frequency makes change in three different positions. It is indicated that the axial-vibration mode results in a severe limitation to the control bandwidth. Furthermore, the ball screw drive is a system with time-varying parametric uncertainties.

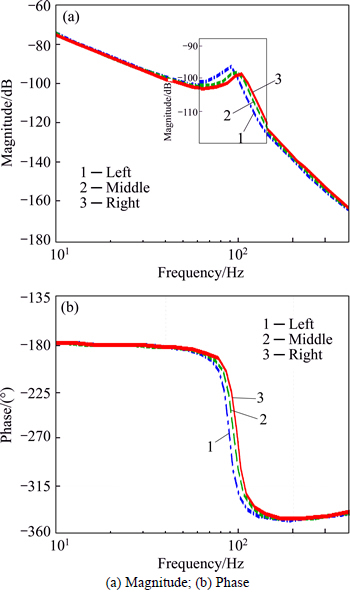
Fig. 2 FRFs of ball screw drive in three different positions:

Since this work focuses on the axial-vibration model, the model of the ball screw drives can be simplified to a two-degree freedom system as shown in Fig. 3. Then the system can be expressed by

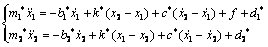   (1)

where m₁^* is the equivalent inertia of rotating parts including motor and ball screw. m₂^* is the equivalent inertia of the table. b₁^* is the viscous damping coefficient of rotating parts, such as the motor and bearings, while b₂^* is the viscous damping coefficient of the guideways. k^* is the overall axial stiffness coefficient affected by preloaded nut, thrust bearing and screw. c is the damping coefficient induced by the preloaded nut. f is the driving force of the motor. d₁^* and d₂^* respectively represent the external disturbances mainly caused by the nonlinear friction and cutting forces, which always act on the revolving components and translating parts. x₁ and x₂ respectively represent the motor rotational displacement and table displacement.

Fig. 3 Two degrees of freedom model

For the control law design, the physical units on both sides of Eq. (1) should be converted from Newton to Volt. Then a motor torque constant K_t[N/V] is divided on the both sides of Eq. (1) and the system can be rewritten as

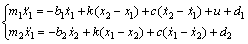      (2)

where u represents the control signal applied to the current amplifier which can be transformed into the driving force by servo motor.

According to Eq. (2), the drive model can be rewritten in state space as

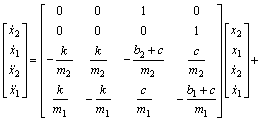
                (3)

Define the state vector as 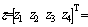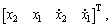and with consideration of the time-varying parametric uncertainties, structural flexibility and the external disturbances, Eq. (3) can be transformed as

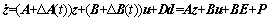   (4)

where △A(t), △B(t) are time-varying vectors caused by the dynamic variations of ball screw drives, and △f₁(t) and △f₂(t) are the time-varying parameters. E and P are respectively the unknown matched and mismatched uncertainties and disturbances. Furthermore, E and P are bounded and given as

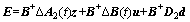               (5)

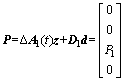                         (6)

where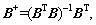

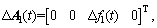
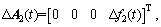
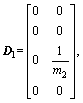
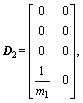
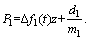
3 Control law design

3.1 Design of AISMC

Since the effects of matched disturbances and uncertainties can be completely counteracted by sliding mode control, an AISMC is designed firstly to ignore the effects of mismatched disturbances and uncertainties. The dimension of the system is as same as the state space in the integral sliding surface compared with traditional sliding mode control. The system trajectory always begins with the sliding surface in integral sliding mode control [19, 20]. As a consequence, the reaching phase is eliminated to guarantee the higher efficiency and robustness of the whole control system.

The sliding surface σ is designed as

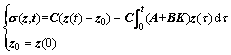         (7)

where C, K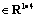 are real constant matrices, moreover, C is designed to guarantee CB nonsingular, z₀ is the initial state of the state vector. When the system state is in the corresponding sliding surface, it can be denoted as 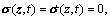there is

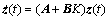                           (8)

to achieve the desired control effect, the matrix K is designed so that all the eigenvalues of A+BK possess negative real parts.

The tracking error is defined as

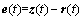                               (9)

where error e and reference vector r are presented as

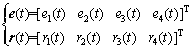             (10)

where r₁(t) and r₂(t) represent the desired displacements, while r₃(t) and r₄(t) are respectively the reference velocities of the table and motor. Moreover, 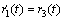and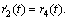

According to Eq. (7), the integral switching function is applied to minimizing the state tracking errors of ball screw drive system, as shown in Eq. (11)

         (11)

where 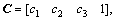and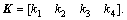

Let 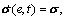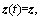r(t)=r, e(t)=e. Differentiating Eq. (11) gives

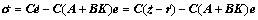   (12)

Substituting Eq. (4) without mismatched disturbances and uncertainties P into Eq. (12) gives

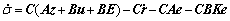
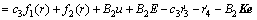  (13)

where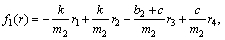

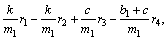
For the satisfaction of the sliding condition, the control law u of the ball screw drive system without mismatched disturbances and uncertainties is designed as

 (14)

where η represents the upper bound on matched disturbances and uncertainties as 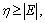and sgn(·) denotes the sign function.

Substituting Eq. (14) into Eq. (13) gives

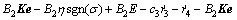
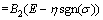                        (15)

Define the Lyapunov function as

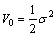                                  (16)

Taking the derivative of V₀ in Eq. (16) gives

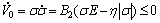                  (17)

Therefore, based on the Lyapunov theorem, the reaching condition is obtained and the AISMC without mismatched disturbances and uncertainties is asymptotically stable.

3.2 Optimal design of state feedback gain matrix K

Regardless of the system disturbances and uncertainties, the state feedback gain matrix K is designed considering the linear time-invariant system and there is

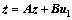                               (18)

The quadratic performance index J is given as

                       (19)

where Q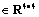 and R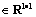 is the symmetric positive definite weighting matrix which needs to be chosen suitably to design the K while ensuring the desired control performance. The optimal control law is given as

                                  (20)

where K^* is the optimal state feedback gain matrix to minimize the quadratic performance index J.

With the given system (18) and the performance index Eq. (19), if the optimization problems of LMIs are defined as

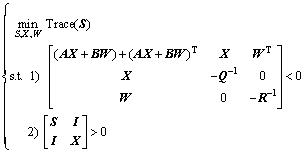(21)

and have solutions 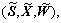then the optimum state matrix K^* of system (17) is given as

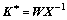                                (22)

where X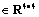is a symmetric positive definite matrix. Meanwhile, the performance upper bound of the corresponding system gives

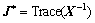                            (23)

3.3 Design of AISMC based on NDO

Since the mismatched disturbances and uncertainties in Eq. (4) mainly exist in the translating parts of the ball screw assembly are hardly be canceled completely by the AISMC, a NDO (nonlinear disturbance observer) [21-23] is designed to compensate the effect of the mismatched disturbances and uncertainties, gives

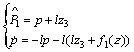                      (24)

where is the estimation of the mismatched disturbances and uncertainties P₁, p and l are the internal state of NDO and observer gain to be chosen, respectively.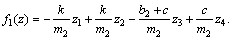

To ensure the stability of the closed-loop system in the sliding mode, a new integral sliding surface is defined combining with the NDO as

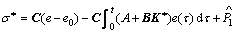       (25)

Then the proposed AISMC control law based on the NDO for the flexible ball screw drive model is obtained as

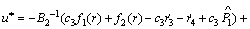
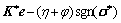                   (26)

where φ represents the switching gain for the mismatched disturbances and uncertainties to be designed.

Taking the derivative of the new sliding surface σ^* to Eq. (25) yields

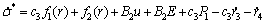
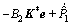                          (27)

Substituting the Eq. (26) into Eq. (27), gives

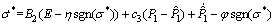 (28)

Define the mismatched disturbances and uncertainties estimation error as

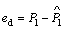                                (29)

According to Eq. (24), the derivative of 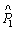can be written as

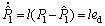                           (30)

Substituting Eq. (30) into Eq. (28) gives

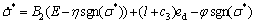    (31)

Consider a new Lyapunov function as

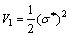                                (32)

Differentiating the V₁ in Eq. (32) gives

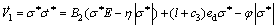 (33)

with the switching gain 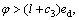the system states will be guaranteed to reach the sliding surface σ*=0 in finite time. Therefore, the AISMC with NDO is asymptotically stable even if both matched and mismatched disturbances and uncertainties exist.

According to the above subsections, the ultimate control law for flexible ball screw drive system is obtained and illustrated in Fig. 4.

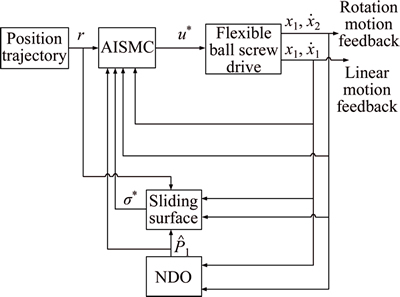
Fig. 4 Block diagram of AISMC with NDO

4 Experimental results

4.1 Tracking performance experiments

The proposed control law was evaluated in the tracking performance experiments conducted with the ball screw drive experimental setup illustrated in Fig. 1. By using the least squares identification techniques, the parameters of Eq. (2) aimed for the experimental setup [24] are listed in Table 1. As a comparison, the P-PI controller with velocity and acceleration feed-forward and friction compensation was applied to the tracking experiments which has a widely usage in the motion control industry. The velocity loop adopted PI (proportional-integral) control and the position loop relied on P (proportional) control. In the displacement of 85.75 mm, a jerk continuous trajectory was taken as the reference signal, and the maximum speed was 0.245 m/s, the maximum acceleration was 0.25 g·m/s², as shown in Fig. 5.

Table 1 Parameters of ball screw drive experimental setup

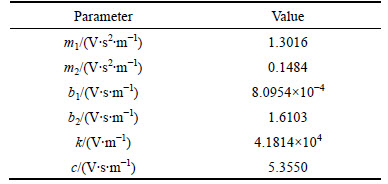
Each test was conducted repeatedly three times in order to confirm the reliability of the experimental results and observe a consistent performance. A 25 kg workpiece mass was used to simulate the mismatched uncertainties of the ball screw drives. Since the workpiece mass cannot be changed during the tracking performance experiments, the time-varying workpiece mass was achieved by placing mass on the table. And the sampling frequency is 20 kHz based on the control algorithms implemented on the dSPACE controller board.

The P-PI controller with velocity and acceleration feed-forward and friction compensation is investigated in Fig. 6. The maximum tracking error is 35.09 μm, as shown in Fig. 6(a). Figure 6(b) indicates that when a 25 kg workpiece is added to the table, the maximum tracking error is increased to 53.27 μm. Furthermore, the tracking error is fluctuating severely during the constant velocity stage. The tracking experiments using AISMC controller are carried out with NDO. Results of these tests are shown in Fig. 7. The maximum tracking error is reduced to 16.43 μm for AISMC with NDO, as shown in Fig. 7(a). And the fluctuation of the tracking error has been significantly reduced for the proposed control law. In Fig. 7(b), the maximum tracking error is increased to about 20.95 μm with a 25 kg workpiece added to the table during the acceleration and deceleration phase. However, the tracking error is almost maintained during the uniform motion and the control signal remains stable.

4.2 Analysis on bandwidth

In the frequency domain experiments, the bandwidths of the closed-loop systems were evaluated in the proposed control law and P-PI controller. A sine sweep signal in range of 10-400Hz was generated as the input signal. And the output signal was the displacement of the table. The closed-loop FRFs are plotted in Fig. 8. According to the figure, the bandwidth of P-PI+Vel+Acc+Fric is 71 Hz. And the proposed control law AISMC+NDO has the higher bandwidth with 162 Hz. There is a consistent relation between the results of bandwidth analysis and the tracking performance experiments, which means that a high bandwidth can improve the response of the system and also ensure the realization of the high tracking precision.

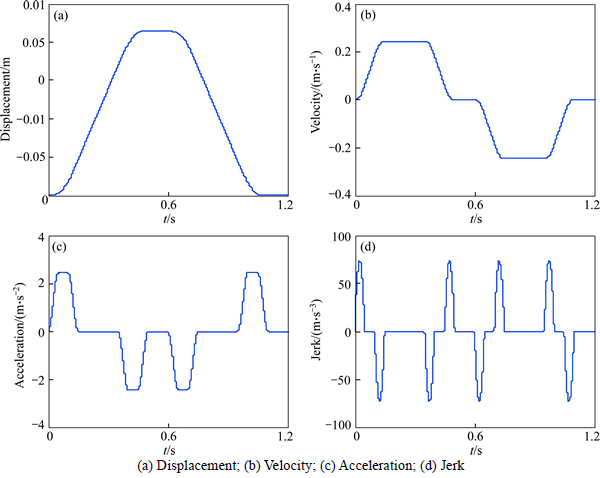
Fig. 5 Reference trajectory:

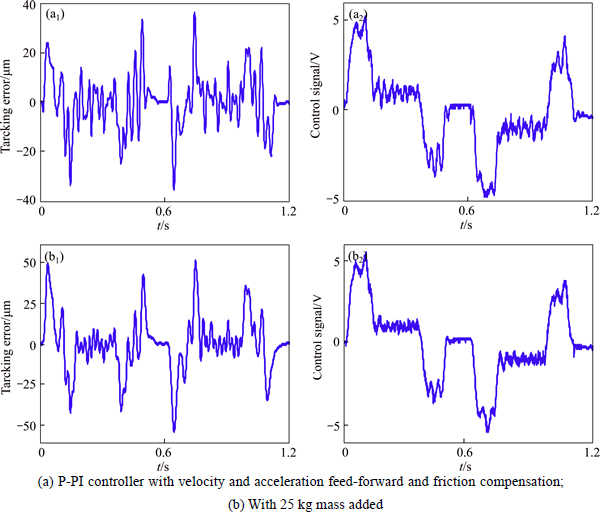
Fig. 6 P-PI tracking experimental results:

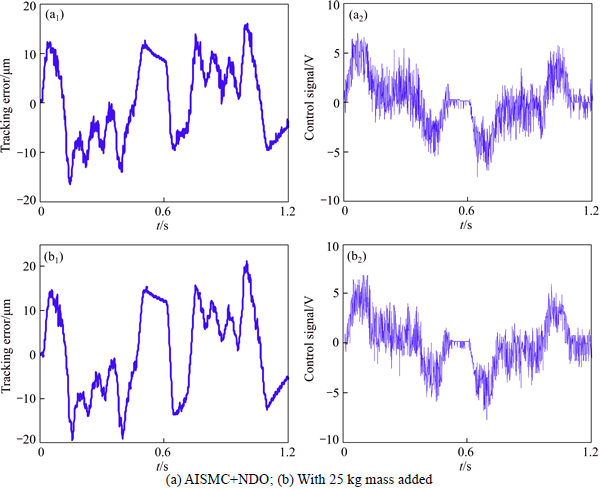
Fig. 7 AISMC tracking experimental results:

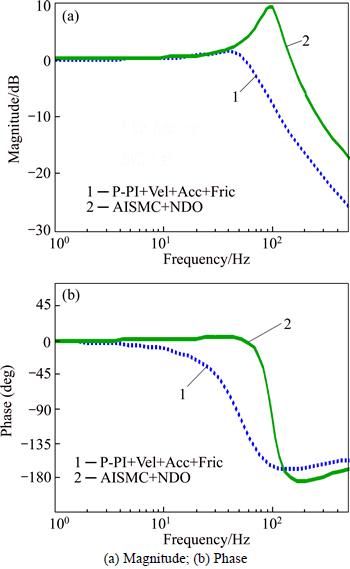
Fig. 8 Closed-loop FRFs of AISMC+NDO and P-PI+Vel+Acc+Fric:

5 Conclusions

1) A higher tracking performance than P-PI controller has been validated based on the proposed control algorithm while obtaining the disturbance rejection.

2) The bandwidth of the closed-loop system has been improved by the proposed control algorithm because of the effect of axial vibration suppression.

References

[1] ALTINTAS Y, VERL A, BRECHER C, URIARTE L, PRITSCHOW G. Machine tool feed drives [J]. CIRP Annals–Manufacturing Technology, 2011, 60(2): 779-796.

[2] DONG Liang, TANG Wen-cheng. Hybrid modeling and analysis of structural dynamic of a ball screw feed drive system [J]. Mechanics, 2013, 19(3): 316-323.

[3] VARANASI K K, NAYFEH S A. The dynamics of lead-screw drives: Low-order modeling and experiments [J]. Transactions-American Society of Mechanical Engineers Journal of Dynamic Systems Measurement and Control, 2004, 126(2): 388-396.

[4] DONG Liang, TANG Wen-cheng, BAO Da-fei. Interpolating gain-scheduled H_∞ loop shaping design for high speed ball screw feed drives [J]. ISA Transactions, 2015, 55: 219-226.

[5] SEPASI D, NAGAMUNE R, SASSANI F. Tracking control of flexible ball screw drives with runout effect and mass variation [J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 1248-1256.

[6] ALTINTAS Y. Manufacturing automation: Metal cutting mechanics, machine tool vibrations, and CNC design [M]. New York: Cambridge University Press, 2012: 25-27.

[7] CHO J U, LE Q N, JEON J W. An FPGA-based multiple-axis motion control chip [J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 856-870.

[8] YAO B, Al-MAJED M, TOMIZUKA M. High-performance robust motion control of machine tools: An adaptive robust control approach and comparative experiments [J]. IEEE/ASME Transactions on Mechatronics, 1997, 2(2): 63-76.

[9] BOUCHER P, DUMUR D, RODRIGUEZ P. Robustification of CNC controllers for machine tools motor drives [J]. CIRP Annals-Manufacturing Technology, 2003, 52(1): 293-296.

[10] LEE K J, KIM H M, KIM J S. Design of a chattering-free sliding mode controller with a friction compensator for motion control of a ball-screw system [J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2004, 218(5): 369-380.

[11] ALTINTAS Y, ERKORKMAZ K, ZHU W H. Sliding mode controller design for high speed feed drives [J]. CIRP Annals-Manufacturing Technology, 2000, 49(1): 265-270.

[12] ERKORMAZ K, KAMALZADEH A. High bandwidth control of ball screw drives [J]. CIRP Annals-Manufacturing Technology, 2006, 55(1): 393-398.

[13] OKWUDIRE C, ALTINTAS Y. Minimum tracking error control of flexible ball screw drives using a discrete-time sliding mode controller [J]. Journal of Dynamic Systems, Measurement, and Control, 2009, 131(5): 051006–12

[14] GORDON D J, ERKORMAZ K. Accurate control of ball screw drives using pole-placement vibration damping and a novel trajectory prefilter [J]. Precision Engineering, 2013, 7(2): 308-322.

[15] DONG Liang, TANG Wen-cheng. Adaptive backstepping sliding mode control of flexible ball screw drives with time-varying parametric disturbances and uncertainties [J]. ISA Transactions, 2014, 53(1): 110-116.

[16] HANIFZADEGAN M, NAGAMUNE R. Switching gain-scheduled control design for flexible ball-screw drives [J]. Journal of Dynamic Systems, Measurement, and Control, 2014, 136(1): 014503.

[17] APKARIAN P, ADAMS R J. Advanced gain-scheduling techniques for uncertain systems [J]. IEEE Transactions on Control Systems Technology, 1998, 6(1): 21-32.

[18] LIAO Yu-lei, ZHANG Ming-jun, WAN Lei, LI Ye. Trajectory tracking control for underactuated unmanned surface vehicles with dynamic uncertainties [J]. Journal of Central South University, 2016, 23: 370-378.

[19] UTKIN V, SHI J X. Integral sliding mode in systems operating under uncertainty conditions [C]// Proceedings of the 35th IEEE Conference on Decision and Control. Lobe, Japan: IEEE, 1996: 4591-4596.

[20] BEJARANO F J, FRIDMAN L M, POZNYAK A S. Output integral sliding mode for min-max optimization of multi-plant linear uncertain systems [J]. IEEE Transactions on Automatic Control, 2009, 54(11): 2611-2620.

[21] CHEN Wen-hua, BALLANCE D J, GAWTHROP P J, O’REILLY J. A nonlinear disturbance observer for robotic manipulators [J]. IEEE Transactions on Industrial Electronics, 2000, 47(4): 932-938.

[22] CHEN Wen-hua. Nonlinear disturbance observer-enhanced dynamic inversion control of missiles [J]. Journal of Guidance, Control, and Dynamics, 2003, 26(1): 161-166.

[23] YANG Jun, LI Shi-hua, YU Xing-huo. Sliding-mode control for systems with mismatched uncertainties via a disturbance observer [J]. IEEE Transactions on Industrial Electronics, 2013, 60(1): 160-169.

[24] ERKORMAZ K, ALTINTAS Y. High speed CNC system design. Part II: modeling and identification of feed drives [J]. International Journal of Machine Tools and Manufacture, 2001, 41(10): 1487- 1509.

(Edited by HE Yun-bin)

Cite this article as: BAO Da-fei, TANG Wen-cheng, DONG Liang. Integral sliding mode control for flexible ball screw drives with matched and mismatched uncertainties and disturbances [J]. Journal of Central South University, 2017, 24(9): 1992–2000. DOI:https://doi.org/10.1007/s11771-017-3608-4.

Foundation item: Project(2013ZX04008011) supported by the National Science and Technology Major Projects of China; Project(51675100) supported by the National Natural Science Foundation of China

Received date: 2016-03-02; Accepted date: 2016-07-10

Corresponding author: TANG Wen-cheng, Professor, PhD; Tel: +86-13337803355; E-mail: 101000185@seu.edu.cn