
Hot deformation behavior and constitutive equations of titanium alloy Ti26
DU Yu(杜宇), QI Yun-lian(戚运莲), ZHAO Yong-qiang(赵永庆), WANG Rui-ning(王蕊宁),
LIU Wei(刘伟), XI Zheng-ping(奚正平), HONG Quan(洪权)
Northwest Institute for Nonferrous Metal Research, Xi’an 710016, China
Received 15 July 2007; accepted 10 September 2007
Abstract: Samples of Ti26 (Ti-V-Sn-Cr-Al-Zr-Nb) alloy were compressed on the Gleeble-1500 heat stimulation machine. The compression test was carried out at 900-1 150 ℃ and strain rates from 0.001 s-1 to 10 s-1. Flow stress data at various temperatures and strain rate were obtained; and the compressive true stress vs. true strain curves were measured and studied. The deformation activation energy was calculated. The results show that the flow stress of Ti26 alloy decreases with the increase of temperature and the decrease of strain rate, and the deformation activation energy is 278.11 kJ/mol in b phase region. The flow stress curves and deformation activation energy reveal that the main softening mechanism is dynamic recovery in b phase region. Constitutive equations were formulated to describe the temperature dependence of the flow stress over a wide range of strain rates.
Key words: Ti26 titanium alloy; hot deformation; activation energy
1 Introduction
The Ti26 (Ti-V-Sn-Cr-Al-Zr-Nb) alloy is based on Ti-15-3 alloy with little alloying element Zr and Nb. This alloy has an advantage over Ti-15-3 in comprehensive mechanical properties on the same conditions. The need to hot work these materials at relatively low temperatures in order to control microstructure and final properties often requires the utilization of isothermal or near- isothermal deformation processing. Many factors can affect the deformation behavior of materials during hot working, such as deformation temperature, deformation rate and deformation degree. The constitutive equation of material can express the relation among the hot working parameter of flow stress, the strain rate and the deformation temperature. The traditional constitutive equation is classified as two groups: the phenomenological and statistical constitutive equation. The phenomenological constitutive equation indicates the physical relationship measured by macroscopic method among the stress, the strain and the strain rate by mathematical statistics method or artificial neural network method, but the micromechanism of relevant atom and the molecular structures was not involved[1-3]. And then the statistical constitutive equation is established on the micromechanism of atom and the molecular model. Actual appliance of engineering widely chooses to use the phenomenological constitutive equation. The processing, heat treatment, mechanical properties, and microstructure of Ti26 alloy were reported in Ref.[4]. The aim of studying hot deformation of the alloy at a given range of temperature and strain rate is to obtain good hot work parameters in this work, which can achieve a perfect combination of the hot work with microstructures and properties.
In this work, the hot deformation behavior of a new metastable β-type titanium alloy was investigated by casting samples under the hot working conditions of varying temperature and strain rate conducted on isothermal compression heat stimulation machine. Hence, the objective of the present paper is to study the influence of the processing temperature, strain rate and deformation degree on the flow stress behavior and to perform constitutive modeling of the hot working process for Ti26.
2 Experimental
The compression specimens were a cast specimen received in the form of as-cast ingot with an outer diameter of 160 mm. The b transus temperature of this alloy is approximately 770 ℃. The specimens were machined into cylindrical shape with 8 mm in diameter and 12 mm in length using linear cutting machine. The hot compression test was carried on Gleeble 1500 simulator. In order to reduce the friction at the die/specimen interface, a graphite foil was inserted between the die and the specimen. A thermocouple was welded at the mid-span of the specimens to provide an accurate temperature control and measurement during testing. The test was conducted at five strain rates (0.001, 0.01, 0.1, 1, 10 s-1) to a deformation of approximately 70% and at six temperatures (900, 950, 1 000, 1 050, 1 100, 1 150 ℃). Specimens were automatic water quenched immediately upon the completion of compression test without moving the specimen from the machine.
3 Results and discussion
3.1 Experiment stress—strain curves
The typical true stress—strain curves obtained at 900 ℃ and 1 150 ℃ in the strain rate range of 0.001-10 s-1 are presented in Fig.1.
In Fig.1 the true stress—strain curve showed a sharp increase in stress at the beginning stage of the test. After the peak stress, the true stress—strain curves dropped continuously and the steady state conditions were not observed even up to a strain value of 0.8. The flow stress increased with increasing strain rates. The difference between the stress—strain behavior of Fig.1(a) and the Fig.1(b) was that the flow stress of Fig.1(a) dropped much faster than that of Fig.1(b).
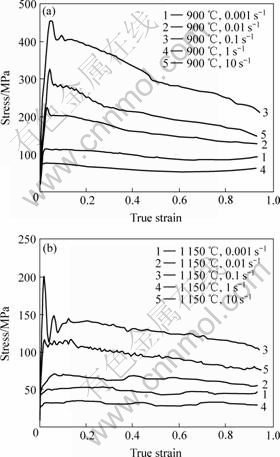
Fig.1 True stress—strain curves of alloy at 900 ℃ and 1 150 ℃ in various strain rates
Fig.2 shows that the flow stress decreased with increasing deformation temperatures at the same strain rate. The flow stress of the alloy in 900-1 150 ℃ increased and reached a peak stress, and then decreased as the strain further increased, and finally reached a steady state. The flow stress essentially remained approximately constant at the high temperature (1 000- 1 1500 ℃) and the high strain rate (10 s-1), which indicates that dynamic recovery occurred during the hot deformation process at a particular temperature and strain rate.
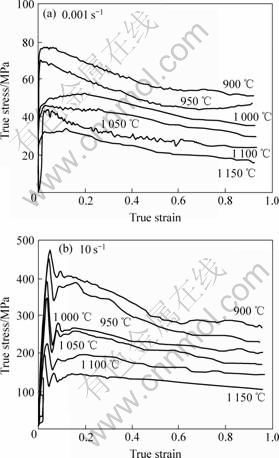
Fig.2 True stress—strain curves of alloy at strain rate 0.001 s-1(a) and 10 s-1(b) at various temperatures
3.2 constitutive relationships and activation energy
The relationships between stress, strain, strain rate and temperature can be described by constitutive equation. There are three Arrhenius type constitutive models that have been widely used to describe the constitutive relationships. They have the following form[5]:
 (1)
(1)
 (2)
(2)
 (3)
(3)
where Q is the apparent activation energy of deformation; n, n1 are the stress exponent; A, A1, A2, and a, b are the material constants; R is the gas constant;  is the strain rate; and T is the absolute temperature. In present study, the Arrhenius-type hyperbolic-sine equation is used to express the hot deformation of Ti26 alloy. The other two Arrhenius-type equations are not further studied here for the reason that Eqns.(1) and (2) are merely extreme cases of Eqn.(3). In Eqn.(3), a is the stress multiplier that provides an adjustable constant to bring as into the correct range in order to generate constant temperature parallel lines in the ln
is the strain rate; and T is the absolute temperature. In present study, the Arrhenius-type hyperbolic-sine equation is used to express the hot deformation of Ti26 alloy. The other two Arrhenius-type equations are not further studied here for the reason that Eqns.(1) and (2) are merely extreme cases of Eqn.(3). In Eqn.(3), a is the stress multiplier that provides an adjustable constant to bring as into the correct range in order to generate constant temperature parallel lines in the ln versus ln sinh(as) plots. As a increases, n decreases to compensate, and the slope of the Arrhenius plot (ln sinh(αs) versus 1/T), rises nearly linearly so that the activation energy, Q levels to a stable value. In this work, the constitutive relation given in Eqn.(3) was used to determine the values for the stress exponent and activation energy for Ti26.
versus ln sinh(as) plots. As a increases, n decreases to compensate, and the slope of the Arrhenius plot (ln sinh(αs) versus 1/T), rises nearly linearly so that the activation energy, Q levels to a stable value. In this work, the constitutive relation given in Eqn.(3) was used to determine the values for the stress exponent and activation energy for Ti26.
In the case of Ti26, the activation energy of single-phase b regions is calculated. The constant temperature logarithmic plots of the flow strain (e=0.6) as a function of the strain rate that gives the best possible linear fits at a a value of 0.009 3 is shown in Fig.3.
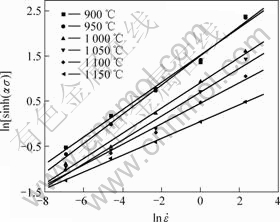
Fig.3 Relationships of ln[sinh(αs)] and ln
At a constant strain rate the logarithmic plot of flow strain (e=0.6) as a function of the inverse of temperature gave linear plots that needed to be modeled for determining the activation energies in the single-phase b regions, as shown in Fig.4. From the regression analysis of the data plotted in Fig.4, the activation energy of the beta regions was 278.11 kJ/mol. The activation energy of IMI834 reported by WANJARA was 153 kJ/mol for the beta. And the activation energy of TA15(Ti-6Al- 2Zr-1V-1Mo ) reported by XU was 205 kJ/mol for the beta.
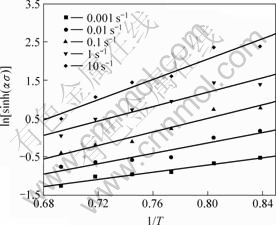
Fig.4 Relationships of ln[sinh(αs)] and 1/T
For pure metals, the apparent activation energy of deformation is often associated with that for self-diffusion. With respect to self-diffusion in the beta phase of pure titanium, BROWN and ASHBY calculated a value of 250 kJ/mol while WALSCOEDE RECA and LIBANATI obtained 152 kJ/mol. DYMENT[6] has found that body centered cubic metals are characterized by a continuous change in their diffusion properties and the self-diffusion rate was determined to increase with temperature up to the melting point. so a range of activation energies for self-diffusion in beta-titanium could be possible. For Ti26, in the beta phase field, the activation energy for deformation are 278.11 kJ/mol. In general, the activation energy for deformation is equal to that for self-diffusion when the controlling mechanism involves dislocation climb. Although the stacking fault energy values have not been determined for the body centered cubic crystal structure of the beta phase of titanium, such a crystal structure leads to a high stacking fault energy and the availability of a large number of slip systems that facilitate easy cross-slip and climb of dislocations in these materials, especially at high temperatures[7]. Hence, dynamic recovery is likely the main controlling mechanism for deformation in the single-phase beta region of Ti26 as observed for IMI834 and Ti-6Al-4V[8].
The apparent activation energy obtained for the deformation of Ti26 in the beta regions was used to correlate the data in terms of the Zener–Hollomon parameter Z, where
 (4)
(4)
The linearity of the data suggests that the flow stress follows the expected trend from Eqn.(4) for strain rate and temperature. The equation of state of the material for deformation can be written as
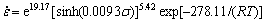
4 Conclusions
1) The true stress—strain curves are very alike. The flow stress of Ti26 alloy decreases with the increase of temperature and the decrease of strain rate. In the b phase region, the flow stress is not sensitive to temperature, and true stress—strain curves remain steady state type at both high and low strain rate.
2) Constitutive equations are formulated to describe the temperature dependence of the flow stress over a wide range of strain rates.
3) In b phase region, the activation energy of 278 kJ/mol is close to that for self-diffusion. The deformation model is dynamic recovery.
References
[1] HONG Q, ZHANG ZH Q, YANG G J, et al. Hot processing and microstructure of Ti600 alloy[J]. Acta Metallurgica Sinica, 2002(38): 135-138.
[2] EYLON D, BOYER R R, KOSS A. β titanium alloys in the 1990s[M]. Warrendale: The Minerals, Metals and Materials Society, 1993: 283-295.
[3] LI Ping, XUE Ke-min, LU Yan, ZHANG Xiao-xia. Experimental studies on hot deformation of Ti-15-3 alloy[J]. Journal of Harbin Institute of Technology, 2000, 32(5): 45-47.
[4] MA Hong-tao, ZHANG Shu-qi, YANG Hai-ying, LI Ming-qiang, ZHANG Wei. A new high strength Ti-26 titanium alloy for fasteners[J]. Acta Metallurgica Sinica, 1999, 35(1): 115-119.
[5] McQueen H J, Ryan N D. Constitutive analysis in hot working[J]. Materials Science and Engineering A, 2002, A322: 43-63.
[6] KIMURA H, IZUMI O. Titanium’80[M]. Warrendale, PA: Science and Technology, TMS, 1980: 519-528.
[7] SHEPPARD T, NORLEY J. Deformation characteristics of Ti-6Al-4V[J]. Materials Science and Technology, 1988(4): 903-908.
[8] ZHOU Min. Constitutive modeling of the viscoplastic deformation in high temperature forging of titanium alloy IMI834[J]. Mater Sci Eng A, 1998, A245: 29-38.
[9] BAO Ru-qiang, HUANG Xu, CAO Chun-xiao, KE Jun. Application of processing maps in hot working of titanium alloy[J]. Journal of Materials, 2004, 18(7): 26-29.
[10] YE Wen-jun, TUO Xiang-ming, WANG Shi-hong. Hot compressive behavior of β21S titanium alloy[J]. Chinese Journal of Rare Metals, 2002, 26(1): 23-27.
[11] XIONG Ai-ming, CHEN Sheng-hui, HUANG Wei-chao, LIN Hai, LI Miao-quan. Investigation on thermal deformation performance of TC6 titanium alloy[J]. Forging & Stamping Technology, 2003(2): 41-43.
[12] CUI Wen-fang, HONG Quan, LIU Chun-ming, ZHOU Lian. Hot deformation behaviours of Ti-1100/0.1Y alloy through isothermal hot compression tests[J]. Journal of Northeastern University (Natural Science), 2003, 24(6): 532-535.
Foundation item: Projects (2007CB613805) supported by the National Basic Research Program of China
Corresponding author: DU Yu; Tel: +86-029-86231078; E-mail:duyu@c-nin.com
(Edited by CHEN Ai-hua)