Trans. Nonferrous Met. Soc. China 20(2010) s937-s942

Stability of steel thixoforming process

J. C. PIERRET, A. RASSILI, G. VANEETVELD, J. LECOMTE-BECKERS

ThixoUnit ULg, Material Sciences Unit, Department of Aerospace and Mechanical Engineering,

University of Liège, Liège 4000, Belgium

Received 13 May 2010; accepted 25 June 2010

Abstract: To improve the industrialization of the process, the study of a thixoforming line stability was proposed. The thixoforming line is fully automated to optimize the repeatability of the experiments. Parameters of the heating cycle, the slug temperature, the tool temperature and the forming speed were studied. For each of them, a range of the expected variations in a steady-state process as well as the effects of these variations on the process itself (forming load and parts quality) were given. These variations are shown to be acceptable. Three different tools were used in the experiments. Some mathematical simulations were realized on the finite elements code Forge2008? with a semi-solid constitutive law. The capacity of the model to represent the process stability was discussed. The simulation results are in agreement with the experiment results.

Key words: thixoforming; steel; high melting point; stability; robustness; process

1 Introduction

Recent studies[1-4] have shown that thixoforming can be applied to steel with good results. Nevertheless, these researches mainly focused on the possibility to shape parts and the quality of these parts. The goal of this work is to bring some new elements about robustness and stability of the steel thixofoming process. In this way, the study focuses on the process sensitivity to a variation of its main parameters and its repeatability for a given set of optimized parameters. The influence of the parameters on the process was determined thanking to the quantification of the forming load and the qualitative observations of the parts quality.

2 Experimental

This research was realized on the pilot thixoforming production line[4] located at the University of Liège (Fig.1). This line is composed of: 1) a feeding treadmill that transports slugs, 2) an inductive heating (150 kW, 2-10 kHz), 3) a high-speed feeding robot, 4) a cleaner-

lubricating robot that also takes parts out of the press, 5) a hydraulic 5 000 kN high-speed press and 6) a cooling/thermal treatment area.

2.1 Direct extrusion tool

During this work, we have used three different tools. The first one (Fig.2), developed in collaboration with the AscoMetal CREAS research center, is a direct extrusion tool that basically consists of a reduction of the slug diameter. The deformation rate is linked to the ratio of slug diameter to channel diameter.

For this tool, the inductive heating is done directly inside the hydraulic press and the die passes through the inductor when the heating is over.

There is no transfer for the heated slug to the tool. At the beginning of the cycle, the slug stands on an inconel 718 punch covered by a Nefacier? (thermal insulator) patch. The punch stands on a load sensor. When heating cycle is finished, the tool will be pushed down through the inductor and forming step occurs. Deformation ends as soon as the two cylinders enter into contact. At this time, the whole tool moves down, digging the damping platform. The consequence is that the load sensor does not measure anything. The lower cylinder height can be adjusted by annular wedges. This setting was done because, classically, using a hydraulic press, the forming speed is variable as there is a decreasing of the punch speed at the end of forming[5-7].

The tool was heated by resistive elements and its temperature was measured by thermocouples. 
 

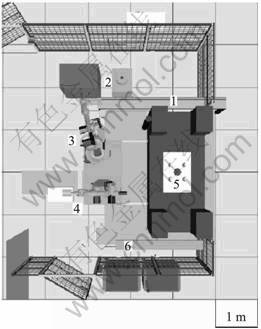
Fig.1 Top view of pilot thixoforming line installed at University of Liège

Fig.2 Direct extrusion tool

2.2 Double-cup tool

The second tool(Fig.3) was developed in collaboration with the ENSAM of Metz. It is made in H11 hot work steel and forms an axisymmetric double-cup part(Fig.5(b)). The deformation is a compression followed by an important reverse extrusion. Due to small thickness of the walls, this geometry highlighted the thermal effects occurring during the  forming. The dies and the punches were instrumented by thermocouples in order to measure their inner thermal fields. At the beginning of the cycle, the tool was open and the punches were out of the dies. When heating was done, robot put the slug in the lower die and moved back. Then, the upper part of the tool moved down to close it and the two punches formed the part. It is also possible to form it with the upper punch alone if the lower one is already inside the die at the beginning of the cycle. This possibility was used to determine friction parameters[8].

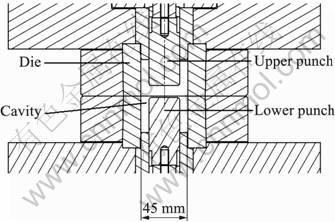
Fig.3 Double-cup tool

2.3 SKL Flange tool

The last tool(Fig.4)[2], developed in collaboration with the Institute of Metal Forming of the University of Hannover (IFUM), allows forming car engine parts (Fig.5). This part is usually formed by hot forming with a great amount of waste. It was re-designed for thixoforming[9]. As this is an industrial part and not a rheological test like the previous ones, the flows are more complex. A specificity of this tool is that it is already closed when the semi-solid material is inserted. The forming is then more faster as the tool closing time is removed from the cycle time. Indeed, for this tool, the cycle begins by the closing of the die during the heating step. Robot then puts the slug in the loading cavity of the tool upper part and moves back. Then, forming is done by the upper punch, lower one is used for ejection after opening of the tool.

Fig.5 shows the geometries obtained with the three  tools. These parts were formed from slug machine in laminated bars of 100Cr6 and C38 steel grades.

3 Modeling

The finite elements(FE) code Forge2008? was used for the simulations. The constitutive law used in this work is quite simple and mainly driven by the liquid fraction, and so the temperature. Thus, the structure of the raw material and its evolution are not explicitly represented. Even if this is a limitation of the calculation results, the error on the flow behavior is low for high solid fraction. Thermal exchanges were already taken into account by the FE code.

Fig.4 SKL Flange tool

Fig.5 Geometries of parts formed with three tools: (a) direct extrusion; (b) double-cup; (c) SKL Flange

The constitutive law is a classical Spittel one (which is the default law used by the solver) when material temperature is lower than solidus and a modification of this Spittel equation when the material temperature is higher than solidus. The modification induces a linear decreasing of the consistency by multiplying it by a factor going from one to zero between the solidus and the liquidus. There is then a smooth transition between semi-solid and solid behavior during cooling.

The constitutive law is

                         (1)

for T < T_sol and

                 (2)

for T_sol < T < T_liq.

In these equations, σ is the stress; ε is the strain;  is the strain rate; T is the temperature; T_liq is the liquidus temperature; T_sol is the solidus temperature and A, m₁, m₂, m₃ and m₄ are constants depending on the steel grade. For 100Cr6 steel, the values of the constant parameters are given in Table 1. The values of A and m₁ to m₄ come from the database of Forge2008? and the values of T_liq and T_sol were obtained by differential scanning calorimetry (DSC)[10].

  4 Results and discussion

4.1 Heating step stability

On our equipment, heating cycles were programmed and applied to the slug without control. It is useful to check that these cycles are repeatable and that final slug temperature is always the same even if the neighboring is not constant. Particularly, our inductors are usually sealed in concrete and those ones tends to heat up as well as the ceramic pedestals on which the slugs stand during heating. Fig.6 shows the measurement results of the final temperature in two points of the slug for a sequence of 10 sequential heating. Slugs have been heated one after another without cooling the inductor at a rate of 75 s per heating. Temperatures have been measured by K-type thermocouples at the center and a point set at mid-height and 3 mm from the lateral surface of the slug. From Fig.6, it can be seen that there is an increasing of  temperature of around 70 ?C between the first and the fifth heating. After that, the final temperature is steady and the difference of the temperature between the hotter and the colder is only 7 ?C.

Table 1 Values of constants used in Eqs. (1) and (2)

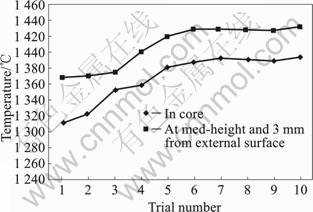
Fig.6 Evolution of slug temperature at end of heating cycle for 10 sequential trials

4.2 Forming step repeatability

Repeatability of the forming load is a good indicator of the process repeatability. Indeed, measured load is the consequence of all the phenomena acting on the deformation and have an impact on the material rheology. Table 2 gives the loads measured during extrusion tests for the sets of parameters. For each of these sets, 5 experiments were realized and the table gives the mean values and the standard deviations.

From Table 2, it appears that loads are repeatable. Usually, the standard deviation is lower than 6%. The only exception is the first set of measurement with higher variation (33%). This is because that the slug temperature corresponds to a high liquid fraction (around 30%) and that the tool was not heated. In these conditions, the flow was turbulent, which is less repeatable. By the way, the quality of the obtained parts was really poor in this case. Beyond the load, the obtained geometries for a single set of parameters were always the same. For all the sets, defects are the same and are localized at the same area. Moreover, if one flow was unstable, all the formings done with the same set of parameters will be turbulent too.

Table 2 Forming load repeatability for direct extrusion

4.3 Forming step stability

It is useful to know the sensitivity of the forming load to the process parameters. Indeed, these ones are more or less controlled in production and so their values are not harshly constant.

The slug temperature(Fig.7), which is directly linked to the liquid fraction, is obviously the parameter that the smallest variation leads to the biggest load variation. It is also well-established that increasing slug temperature leads to decreasing the forming load[1]. This effect is mainly visible for the direct extrusion as, in this case, a variation of less than 2% (20 ?C) brings to an increasing of load of more than 50%. For the double-cup part, the sensibility is clearly lower. This could be explained by two factors. First one is that the volume of the slug is lower in the case of direct extrusion than for the double-cup part (“H”Part) (32 000 vs. 53 000 mm?). So the thermal inertia is also higher and the semi-solid material keeps its thixotropic and pseudoplastic behavior for a longer time. The second factor is that for the double-cup part, the flow was stable for all the experiments when, for increasing temperature in the case of direct extrusion, it was more and more unstable with liquid-solid segregation(Fig. 8). It is shown that unstable flow leads to higher forming loads than stable flow does[11]. This instability is a detrimental consequence of a too high slug temperature. A second bad effect is the increasing of defects (cracks, shrinkage porosities, etc) occurrences when this temperature is too high[12].

In our installation, the heating accuracy is around  7℃ for a maximum temperature of about 1 400 ?C, so  a variation of 0.5%. As it is an industrial device, we could postulate that industrial equipment could reach such accuracy. For this temperature variation, the load variation is 15% in the case of direct extrusion but less than 5% in the case of the double-cup part.

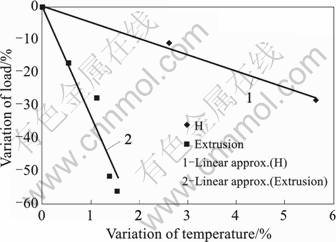
Fig.7 Influence of slug’s temperature on measured forming load

Fig.8 Influence of tool temperature on flow stability

Tool temperature (Fig.9) is the worst regulated parameter, and so the one for which variations are the largest. However, we have not observed bad consequences on the flow of high tool temperature. Heating the tool decreases the thermal exchanges and then slows down the drop of slug’s temperature. This leads to a higher fluidity of the semi-solid material during the whole forming step and decreases the forming load[5]. A second advantage of a high tool temperature is forming the semi-solid material at higher temperature without emergence of instabilities[6]. The only reason to limit this parameter is to keep sufficient tool mechanical resistance. It is only necessary to provide a temperature for stable flow, so high enough to reduce freezing flow. In this case, the load will stay low. Fig.9 shows a great sensibility of the load to the tool temperature. It must nevertheless be said that the reference point is room temperature (20 ?C). The graph shows mainly the necessity to heat the dies. For industrial production rate, however, tools could be heated only by the slugs, in this case, dies and punches would probably have to be cooled in order to keep a sufficient mechanical strength.

Fig.9 Influence of tool temperature on measured forming load

Variation of load with the forming speed (Fig.10) is due to shear-thinning behavior of the semi-solid material and thermal exchanges with the tools[4]. Shear-thinning behavior means that forming resistance decreases when shearing rate, linked to deformation rate, increases. This effect is usually explained by the breaking of bonds between solid grains with the increasing of shearing rate[13-14]. Forming speed has also an effect on the thermal exchanges between slug and tool. Indeed, if forming speed increases, forming time will be shorter and thermal exchanges sill be then lower. As the two consequences of high forming speed lead to decreasing of the forming load, it is possible to fill a die with a lower temperature slug by increasing its forming speed. This modification should bring to a better part quality[11]. The two effects (shear-thinning behavior and thermal exchanges) are nevertheless hard to uncouple as it is impossible to make isothermal experiments for steel thixoforming. Forming speed also has an impact on the semi-solid material flow and could help to stabilize it[3].

Fig.10 Influence of forming speed on measured forming load

The speed accuracy mainly depends on the kind of press. In the case of a hydraulic press, as the one used during this study, two effects must be taken into account. First one is the speed regulation. Measured real speed variations usually don’t exceed 5% from one test to the other (for the same forming conditions), which correspond to a load variation of less than 6% in the direct extrusion case that seems to be the most sensitive one. Second effect is the speed damping at the end of the displacement, which means that the end of the forming is done at very low speed whatever the programmed speed is. The only trial that is not subject to this effect is the direct extrusion one as the damping is rejected to the platform movement. The curve related to this experiment is thus the one which give the best render of the forming speed sensibility. In the other two cases, this is mainly thermal effects that apply through an increasing of the forming time. As this time is no longer directly proportional to the programmed forming speed, curves of Fig.10 are biased (excepted for direct extrusion). The sensitivity of this tool to the forming speed seems, nevertheless, to be low enough.

4.4 Forming simulations

Despite its simplicity, the used model gives a good representation of the semi-solid material behavior as long as its solid fraction is high ( f_s > 0.75). Fig.11 compares the loads measured during the forming of a car engine part to the ones obtained by calculation. They are clearly close one to each other even if there are some discrepancies on the curves shapes. There are two explanations for these differences: on one hand, the model does not take into account the grains agglomeration-disagglomeration phenomena, which have an impact on the semi-solid steel rheology depending on liquid fraction and shearing rate; on the other hand, the simulation considers a constant forming speed that is not reached during actual forming due to speed damping at the end of the slope.

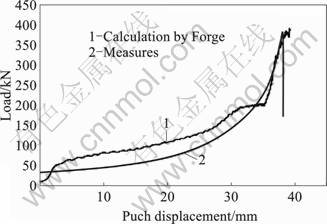
Fig.11 Comparison of loads measured and calculated by FE code Forge2008? during thixoforming of car engine part

It is also important to check that material flows are well-represented by the calculation. Fig.12 shows the material structure, revealed by Béchet-Beaujard etching and superimposes on it the marking grid obtained by calculation on the FE code. The correlation of the grid to the flow is clear.

Fig.12 Comparison of the material structure revealed by etching to the marking grid calculated by Forge2008?

Simulations have been realized with different values of the forming parameters in order to check if the model is able to correctly represent the influences of each of these parameters on the forming, and mainly on the forming loads. Some points on the Figs.9 and 10 have been obtained by calculation instead of measurement (marked as “simulation” and with a different mark than the measured values). The “H” tool has been chosen for these calculations as it is the easiest one to simulate. One can check on the two figures that the simulation results are in accordance with the practical experiments.

5 Conclusions

1) Heating step is of first importance in thixoforming as the slug temperature and its homogeneity manages the deformation behavior.

2) Forming load is also highly repeatable as long as the flow is kept laminar by controlling speed and slug temperature.

3) Sensitivity of the forming step to its main parameters (slug and tool temperature and forming speed) is quite high and depends on the part geometry. Nevertheless, in the range of variation expected in industrial production, the load and parts quality variation is low enough.

4) A quite simple rheological model could correctly simulate the semi-solid steel behavior as long as its liquid fraction is kept low.

Acknowledgements

The authors gratefully acknowledge the University of Liège, the First Europe Project, the COST541 action and the Walloon Region for their financial support. Misters Dirk Fischer and Marc Robelet are also thanked for their valuable scientific suggestions and comments.

References

[1] HIRT G, KOPP R. Thixoforming: Semi-solid metal processing[M] Weinheim: Wiley-VCH Publisher, 2009.

[2] FISCHER D. Development of a fully automated production process for the manufacture of steel parts by thixoforging[D]. Hannover: IFUM Uni-Hannover, 2008.

[3] CEZARD P. Impact of thermal effects on the material behavior during forming of steels in semi-solid state: Experimental and numerical analysis[D]. Metz: ENSAM Metz. 2008.

[4] PIERRET J C, RASSILI A, VANEETVELD G, LECOMTE-BECKERS J, BIGOT R. Robustness of a thixoforming production line[J]. Solid State Phenomena, 2008, 141/143: 207-212.

[5] CEZARD P, BIGOT R, BECKER E, MATHIEU S, PIERRET JC, RASSILI A. Thixoforming of steel: New tools conception to analyze thermal exchanges and strain rate effect[C]∥ Proceedings of the 10^th ESAFORM Conference on Material Forming – AIP Conf. Proc. 2007: 1155-1160.

[6] BECKER E, CEZARD P, BIGOT R, LANGLOIS L, FAVIER V, PIERRET JC. Steel thixoforging: heat exchange impact on the mechanical and metallurgical features of thixoforged samples[J]. Solid State Phenomena, 2008,141/142/143: 701-706.

[7] VANEETVELD G, RASSILI A, PIERRET J C, LECOMTE-BECKERS J. Extrusion test of 7075 aluminium alloys at high solid fraction [J]. International Journal of Material Forming, 2008(s1): 1019-1022.

[8] PIERRET J C, RASSILI A, VANEETVELD G, BIGOT R, LECOMTE-BECKERS J. Friction coefficients evaluation for steel thixoforging[J]. International Journal of Material Forming, 2010, 3(s1): 763-766.

[9] BEHRENS B A, FISCHER D, HALLER B, RASSILI A, PIERRET J C, KLEMM H, STUDINSKI A, WALKIN B, KARLSSON M, ROBELET M, NATALE L, ALPINI F, Series production of thixoformed steel parts[J]. Solid State Phenomena, 2006,116/117: 686-689.

[10] LECOMTE-BECKERS J, RASSILI A, ROBELET M, PONCIN C, KOEUNE R. Study of the liquid fraction and thermophysical properties of semi-solid steels and application to the simulation of inductive heating for thixoforming[J]. Advanced Methods in Material Forming, 2005: 321-347.

[11] ROUFF C. Contribution to characterization and modeling of semi-solid state steel–application to thixoforming[D]. Metz: ENSAM Metz, 2003.

[12] PIERRET J C, RASSILI A, VANEETVELD G, CEZARD P, BIGOT R, LECOMTE-BECKERS J. Steel thixoforming, influence of forming parameters on the microstructure[J]. International Journal of Material Forming, 2008,1(s1): 1011-1014.

[13] FAN Z. Semi-solid metal processing[J]. International Materials Review, 2002,47(2): 49-85

[14] JOLY P A, MEHRABIAN R. The rheology of a partially solid alloy [J]. Journal of Material Science, 1976, 11: 1393-1418.

(Edited by LIU Hua-sen)

Foundation item: Project (415814) supported by the FIRST Europe, THIXOFROR.

Corresponding author: PIERRET Jean-Christophe; Tel: +32-4-3615946; E-mail: jc.pierret@ulg.ac.be