J. Cent. South Univ. (2012) 19: 1466-1474 

DOI: 10.1007/s11771-012-1163-6

A novel conditional cell transmission model for oversaturated arterials

WANG Ping(王屏)¹, L. S. Jones², YANG Qun(杨群) ¹

1. Key Laboratory of Road and Traffic Engineering of Ministry of Education,Tongji University, Shanghai 201804, China;

2. Department of Civil, Construction, and Environmental Engineering,The University of Alabama, Tuscaloosa, AL 35401, USA

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: The objective of this work is to develop a novel feature for traffic flow models, when traffic queues on two-way arterials periodically extend until then they block an upstream signal in oversaturated conditions. The new model, proposed as conditional cell transmission model (CCTM) has been developed with two improvements. First, cell transmission model (CTM) is expanded for two-way arterials by taking account of all diverging and merging activities at intersections. Second, a conditional cell is added to simulate periodic spillback and blockages at an intersection. The results of experiments for a multilane, two-way, three-signal sample network demonstrate that CCTM can accommodate various traffic demands and accurate representation of blockages at intersections. The delay of left turns is underestimated by 40 % in moderate conditions and by 58% in oversaturated condition when using the CTM rather than CCTM. Finally, the consistency between HCS 2000 and CCTM shows that CCTM is a reliable methodology of modeling traffic flow in oversaturated condition.

Key words: oversaturated condition; conditional cell transmission model; intersection; spillback; traffic blockage

1 Introduction

Fifteen large cities lose nearly one billion RMB Yuan per day due to traffic congestion in China in 2010 [1]. Urban arterials operating in oversaturated conditions are now very common and are expected to become even more prevalent. Consequently, there is an urgent need to investigate ways to relieve oversaturated conditions.

In Ref. [2], oversaturation is defined as the condition when vehicles are prevented from moving forward freely. Oversaturation occurs either because of the presence of an excessive demand of vehicles in the intersection itself or because of queue backs up into any of the exit links of an intersection. 

In order to develop traffic control solutions to reduce congestion and mitigate its impacts, traffic simulation is an important tool for analyzing traffic engineering problems and potential solutions [3-4].  Simulation of congested, oversaturated conditions, however, has proven difficult and many available tools do not adequately model such conditions [5-6]. Therefore, improvements of existing traffic flow model simulation techniques are necessary to adequately study such fully oversaturated arterials. This research aims to develop a traffic flow feature to improve the modeling of two-way arterials so that they are capable of modeling oversaturated conditions.

The cell transmission model (CTM) is a potential simulation tool because it can accommodate all traffic conditions from light condition to oversaturated condition [7-8]. In the past decade, CTM has emerged as an alternative tool for investigating traffic flow phenomenon, using discrete space and time scales, which makes it simple to understand and fast to simulate [9-15]. Validation studies of CTM using field data suggest that it is capable of modeling various traffic conditions on both freeways and arterials [16-17].

Even though the CTM is able to accommodate all traffic conditions, it has limitations. First, until recently, CTM-based studies have been limited to one-way arterials. Two-way arterials have more diverging and merging activities at intersections, which makes coding of the CTM more complex and time-consuming. Second, current formulations of the CTM do not simulate blockages at intersections. So, they do not capture the delay originating at oversaturated intersections, and its effects on all movements at the intersection or those upstreams.

The objective of this work is to propose, develop and test an improvement to CTM to improve its ability to model oversaturated traffic flow on a two-way arterial.  Specifically, a new feature, the conditional cell, is presented to model traffic flow dynamics created by the merging and diverging activities on two-way arterials and capture the blockages, spillback and shock wave phenomena attributed to the oversaturated arterial operations.

The major innovations of conditional cell transmission model (CCTM) are as follows:

1) CCTM may be used to simulate traffic conditions in two-way arterials. The CTM simulates traffic conditions in one-way arterials, thus offering limited applicability in the real world. Since two-way arterials are more common than one-way arterials in the real world, CCTM has the potential for more wide-spread use than the CTM.

2) CCTM uses a conditional cell to simulate the spillback and blockages at an intersection. This feature gives CCTM an advantage over traditional simulation software including CORSIM, AIMSUN, VISSIM, etc in modeling traffic flow.

3) In CCTM, users may input the probability of a conditional cell and the probability of the occurrence of a useful gap to match the behaviors of local drivers. This feature is a unique contribution of CCTM.

4) This is the first time that a simulation model (i.e., CCTM) has been able to identify the specific delay contributions associated with conditional blockage of an intersection related to gaps in the opposing flow. Such information would be useful to law enforcement officials.  CCTM can assess the effectiveness of increased enforcement of the “DO NOT BLOCK THE INTERSECTION” driving rule as a way to reduce traffic delay. 

2 Formulation of conditional cell transmission model

2.1 Modeling two-way flow using CCTM

To model two-way flow, all possible turning movements must be considered including the turns from minor streets to the two-way major arterial and turns from the two-way major arterial to minor streets at a two-way intersection. Figure 1 shows that these turning movements generate many diverging and merging activities at a typical two-way intersection [18]. 

A major reason that the CTM has not been developed for two-way arterials is that traffic flow is much more complex than that on one-way arterials.  The complexity lies in two aspects:

1) There are more diverging and merging activities at a two-way intersection.

2) There are only two flows that diverge from a cell in one-way flow; whereas, there could be three flows diverge from a cell in two-way flow.

Fig. 1 Traffic flow movements at typical two-way intersection

Formulations of both mergence and divergence in two-way flow are discussed.

1) Divergence formulation

At the intersection, some vehicles go through while other vehicles make left or right turns. In oversaturated conditions, two spillback situations involving left turns might occur. One situation involves the overflow of vehicles waiting to turn left, which blocks the through-lane entrance. The other situation is the overflow of through vehicles, which blocks the left-turn entrance.

For both situations, all flows are restricted if either the left-turn lane or through-lane is unable to accommodate its allocation of flow [12]. A vehicle that cannot exit its cell will prevent the movement of all vehicles following it. In CCTM, this is captured by using cells which represent homogeneous segments of the traffic network.  CCTM can capture such a phenomenon using the diverge formulation.

The difference between diverging activities of one-way flow and those of two-way flow is that there are only two flows that diverge from a cell in one-way flow, and there could be three flows that diverge from a cell in two-way flow, as shown in Fig. 2.

Fig. 2 Divergence in two-way flow

In Fig. 2, Cell a is the start of a divergence to Cell b, Cell c and Cell d, where Cell b is for left turns, Cell c is for through vehicles, and Cell d is for right vehicles.  The proportions of Cell a outflow going to Cell b, Cell c and Cell d are equal to α, β and γ, respectively. Then, inflow into Cell b, Cell c and Cell d is      

    (1)

Thus, the inflows into Cell b, Cell c and Cell d are

f_b=α×f_b+c+d                                                      (2)

f_c=β×f_b+c+d                                   (3)    

f_d=γ×f_b+c+d                                   (4)

At a typical two-way intersection, there are four diverging points, as shown in Fig. 1. Divergence formulations on these four points may be applied to modeling traffic flow at a two-way intersection.

2) Mergence formulation

At an intersection, through vehicles and other left-turn and right-turn vehicles merge to a receiving lane.  The turning flow is also governed by the available space in the next cell. Turning movements are difficult to formulate because two cells flow into the same cell. As mentioned in the basic formulation of the CTM, the flow between cells at time t is governed by the number of vehicles in the preceding cell n_i-1(t), the inflow capacity Q_i(t), and the available space in the next cell N_i(t)-n_i(t) [11]. 

The difference between merging activities of a one-way flow and those of a two-way flow is straightforward. There are only two flows that merge to a cell in one-way flow; whereas, there could be three flows that merge to a cell in two-way flow, as shown in Fig. 3.

Fig. 3 Mergence in two-way flow

The flow from Cell a to Cell d can be formulated as follows:                         

           (5)

Similarly, the flows from Cell b and Cell c to Cell d can be formulated as follows: 

           (6)

          (7)

Thus, the sum of outflows from Cell a, Cell b, and Cell c to Cell d are noted as

                  (8)            

At a typical two-way intersection, there are four merging points, as shown in Fig. 1. Mergence formulation on these four points may be applied to modeling traffic flow at a two-way intersection.    

2.2 Adding conditional cell to simulate spillback and blockages at intersection

The first improvement to the CTM allowed CCTM to simulate the traffic flows on two-way arterials. The second improvement to the CTM enabled CCTM to model blockages at intersections by adding the conditional cell to simulate spillback and blockages. 

Blockages are characteristics of oversaturated two-way arterials. They can occur in segments and at intersections. For example, left turns can be blocked by the oversaturated through traffic from the same direction or the spillback of through traffic from the opposite direction. The former is a blockage in a segment, and the later is a blockage at an intersection.

Blockage either prohibits the desired movements or increases delay. Therefore, identifying and accounting for blockages is critical to estimate delay. By adding the conditional cell at intersections, CCTM is able to simulate blockages and spillbacks and thus estimate the corresponding delay. The following explains the methodology of the conditional cell in detail.

“DO NOT BLOCK THE INTERSECTION” marking is used to mark the edges of an intersection area that is in close proximity to a signalized intersection, railroad crossing, or other nearby traffic control that might cause vehicles to stop within the intersection and impede other traffic entering the intersection [19]. Vehicles are not permitted to stop inside an intersection if there is not enough room for them to clear the far side of the intersection. Most drivers obey the rule; however, many do not. The traffic queues that form at signalized intersections may “spillback” and block access into or out of a minor street. For example, Fig. 4 shows a westbound left turn blocked by the spillback of eastbound through vehicles. The eastbound through vehicles spill back into the intersection due to the oversaturation. The overflow vehicles occupy the space inside an intersection where the westbound left turn needs to cross thus causing a blockage. (Note: This blockage does not occur in non-oversaturated condition, since through vehicles are processed and do not stop inside the intersection.)

CCTM allows for the possibility of an additional cell forming within an intersection to account for any vehicle that may “caught” there for some amount of time thereby incurring delay and potentially causing delay to conflicting movements. The cell exists conditionally, depending on whether or not there is a spillback at the intersection. In other words, if a spillback occurs, the conditional cell exists and stores the vehicles which accumulate inside the intersection. If a spillback does not occur, the conditional cell will not exist.

Fig. 4 Westbound left turn blocked by spillback of eastbound through vehicles

CCTM uses two events to model this blockage.  First, it uses a conditional cell to simulate the spillback at an intersection. Then, when the conditional cell appears, CCTM determines whether the cell is full or whether there is an acceptable gap inside the conditional cell to allow a left turn.

1) Simulating spillback at an intersection

In Fig. 5, there is a conditional cell between Cell a and Cell b. It holds the spillback vehicles when Cell b is fully occupied and cannot accommodate any more vehicles from Cell a.

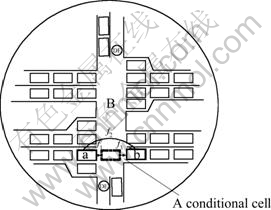
Fig. 5 Adding conditional cell to hold spillback vehicles at intersection

The flow from Cell a is controlled by several factors.  The first controlling factor is the signal status. Cell a is close to the signalized intersection; therefore, the flow occurs during signal green time. The second controlling factor is the availability of space in Cell b. If Cell b is empty or has available space, the flow will go to Cell b (shown by f₂ in Fig. 5). If Cell b is full, the flow will go to the conditional cell (shown as f₁ in Fig. 5), causing a spillback queue at an intersection. The spillback vehicles wait in the conditional cell for the dissipation of the queue and then go to cell b (shown by f₃ in Fig. 5).

The calculations for f₁, f₂ and f₃ are described.

The flow into the conditional cell is calculated by using the number of vehicles in Cell a, the available space in the conditional cell and the flow capacity of the conditional cell. Mathematically, it is expressed as

   f₁=min(n_a, Q_con, (N_con-n_con))                     (9)

where f₁ is the flow from Cell a into the conditional cell in time step t; n_a is the number of vehicles in Cell a in time step t; Q_con is the flow capacity of the conditional cell in time step t; n_con is the number of vehicles in the conditional cell in time step t; N_con is the vehicle holding capacity of the conditional cell.

The flow into Cell b is calculated by using the number of vehicles in Cell a, the available space in Cell b, and the flow capacity of Cell b. Mathematically, it is expressed as

f₂=min(n_a, Q_b, (N_b-n_b))                        (10)

where f₂ is the flow from Cell a into Cell b in time step t; n_a is the number of vehicles in Cell a in time step t; Q_b is the flow capacity of Cell b in time step t; n_b is the number of vehicles in Cell b in time step t; N_b is the vehicle holding capacity of Cell b.

The flow from the condition cell to Cell b is calculated by using the number of vehicles in the conditional cell, the available space in Cell b, and the flow capacity of Cell b. Mathematically, it is expressed as

f₃=min(n_con, Q_b, (N_b-n_b))                      (11)

where f₃ is the flow from the conditional cell into Cell b in time step t; n_con is the number of vehicles in the conditional cell in time step t; Q_b is the flow capacity of Cell b in time step t; n_b is the number of vehicles in Cell b in time step t; N_b is the vehicle holding capacity of  Cell b.

2) Judging availability of acceptable gap

When there is a green signal indication for the westbound left turn, these vehicles need to cross the conditional cell and go to the minor street. Before they make the left turn, they need to judge whether there is an acceptable gap in the conditional cell for them to cross.  If the conditional cell is fully occupied by 13 spillback vehicles, then there is no gap and the vehicles are blocked (See Fig. 6). If a gap exists in the conditional cell, the width and location of the gap determine whether it is an acceptable gap. First of all, the gap should be wide enough. Its width must be larger than one vehicle.  Even if the gap is wide enough, if the location of the gap is not suitable, vehicles still cannot cross it. If the location is suitable, vehicles will use the gap to make the desired movement. The location may be at the end of the queue or may be in the middle of the queue. It depends on the characteristics of local drivers. Some drivers will leave a useful gap accessible to the minor street; others will not thus blocking access into or out of a minor street.

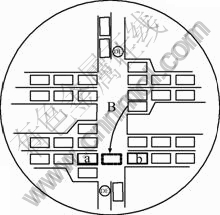
Fig. 6 Left turn blocked by queue spillback

Figure 7 explains the concept of an acceptable gap. The conditional cell holds some spillback vehicles and has a gap. Is the gap wide enough for vehicles making a left turn? Is the location of the gap accessible to the minor street? Figure 8 illustrates various situations of a gap.

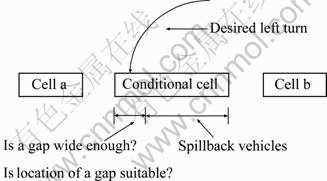
Fig. 7 Concept of acceptable gap

3 Comparisons of CTM and CCTM in terms of delay

To ensure that CCTM performed as expected, a series of experiments were designed and conducted. The results of each experiment were compared between CCTM and CTM. The delay was chosen as the performance measure of the model since CCTM or CTM provides a convenient method to estimate the delay.

3.1 Sample network

A three-signal two-way arterial network was studied, although CCTM can be applied to a larger network. The sample network consists of three intersections. It has a two-way, four-lane major arterial which has four links labeled 1, 2, 3 and 4, and three minor links (minor streets) which are labeled 5, 6 and 7.  Link 5 and Link 7 are one-way, one-lane streets, and Link 6 is two-way, two-lane street.

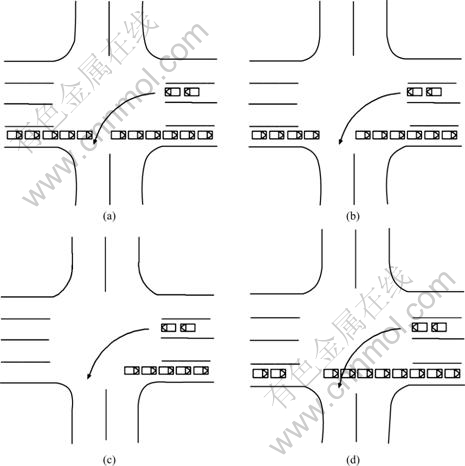
Fig. 8 Various situations of gap: (a) Not wide enough; (b) Useful gap; (c) Useful gap; (d) Location of gap not suitable

To simulate the traffic flow using CCTM, the transportation network was divided into homogeneous cells, as shown in Fig. 9. A cell in Fig. 9 may be specified by the number of the link, the number of the lane, and the number of the position. For example, Cell (1, 2, 3) is in Link 1, Lane 2 and Position 3. Cells where vehicles enter the network are denoted as OR, and cells where vehicles leave the network are denoted as DE. 

3.2 Input and results

1) Input values

(1) Possibility of conditional cell: For comparison purposes, the possibility parameters were assumed to be 0% (used in the CTM) and 100% (used in CCTM);

(2) Possibility of occurrence of a useful gap was 10%;

(3) Traffic demand: Three scenarios of traffic demands on each lane of the network were used: Light –360 vehicles per hour per lane with initial density of 0.4 jam density, Moderate -1.080 vehicles per hour per lane with initial density of 0.75 jam density, and Heavy    -1 800 vehicles per hour per lane with initial density of jam density.

(4) Traffic signal timing: This is shown in Table 1.

2) Results

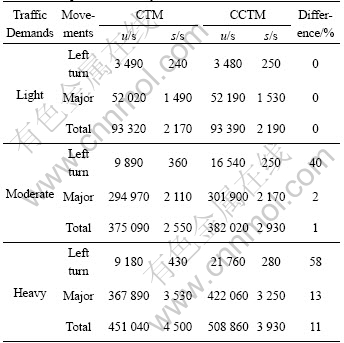
Results of delays at light, moderate and heavy traffic demands are recorded in Table 2.

3.3 Minimum repetitions

The delay in Table 2 is an average value of multiple simulation runs. Due to the stochastic feature of the saturation flow rate between cells, the CTM and CCTM were run multiple times in order to conduct statistical tests of difference.

Regarding the minimum number of model run repetitions, the guidelines of the Traffic Analysis Toolbox [20] was followed. This is a step required to determine if delays of the CTM and CCTM are significantly different.

The difference between CCTM and CTM at heavy traffic demand is most interested in this work, so comparison of their delays of left turns at heavy traffic demand is shown for illustration purposes.

1) Estimation of pooled standard deviation

           (12)

2) Selection of desired confidence level

A 95% confidence level is typically selected for hypothesis testing.

3) Selection of minimal difference in the means

=21 760-9 180=12 580 s                 (13)

4) Computation of minimum repetitions

If the required number of runs is greater than the preliminary number of runs, the analyst performed the additional repetitions for each alternative and recomputed the mean difference and standard deviation using the augmented set of model run repetitions. Referring to the Traffic Analysis Toolbox [20], four repetitions of each alternative are required to reject the hypothesis that the observed differences in the simulation results for the two alternatives could be the result of random chance. Ten repetitions, greater than required, are used in this work.

Fig. 9 Layout of two-way, three-signal arterial network

Table 1 Phase diagram of experiments

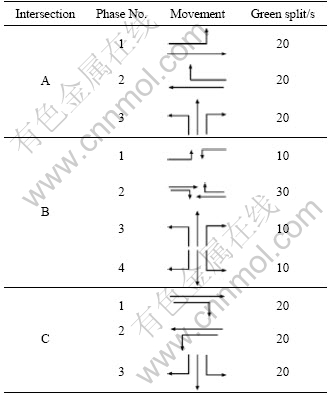
Table 2 Comparisons of delays between CTM and CCTM

3.4 Hypothesis testing

To determine whether simulation output provides sufficient evidence that one alternative is better than the other, it is necessary to perform a statistical hypothesis test of the difference of the mean results for each alternative.

Hypothesis testing for two alternatives:

Null hypothesis H₀: μ_x-μ_y =0

    Against H₁: μ_x-μ_y ≠0

Solution:

=340       (14)

=12 580>340                           (15)

The null hypothesis is rejected. The difference between the delays of left turns from the CTM and CCTM is statistically significant.

3.5 Discussion

From Table 2, it is seen that in light conditions, there is no difference between the CTM and CCTM. In light conditions, there are no spillbacks, because a network can accommodate traffic demands. There is no need for the conditional cell. In moderate conditions, there are some differences between the CTM and CCTM. Compared to CCTM, the CTM underestimates a delay of left turns by 40%. This is because the CTM does not account for the delay when left turns are blocked by the spillback at an intersection. The CTM assumes that drivers will not break the rule if there is no room for them in the far side of the intersection. In many urban areas, this assumption is not consistent with the reality. CCTM overcomes this disadvantage by adding conditional cells at an intersection. Evidence shows that drivers sometimes break the rule even when there is no room for them at the far side of the intersection. Therefore, spillback vehicles enter a conditional cell and block access into or out of minor streets. In other words, vehicles on the major street are prevented from making left turn onto the minor street during green signal time, and this situation causes additional delay. As evidenced by Table 2, the delay of left turns is underestimated by  58% in this example when using the CTM rather than CCTM when traffic demand is heavy.

In additional, CCTM can simulate phenomena in a segment in oversaturated conditions, which includes time when through flow blocks the left turn bay, left turns block the through lane, and shock waves. Meantime, the unique contribution of CCTM is that it can simulate the blockages at an intersection by adding a conditional cell at an intersection. The conditional cell holds vehicles that break the driving rule “DO NOT BLOCK THE INTERSECTION”. Then, CCTM uses the conditional cell to delineate the blockages of other movements caused by the spillback vehicles.

This following discussion provides two illustrations of how CCTM models phenomena that occur frequently in oversaturated conditions.

1) Through flow blocking a left turn bay

As shown in Fig. 10, at the intersection A, there is a left turn bay in addition to the through lane. The overflow of through vehicles can be seen to block the left turn lane, which is a normal phenomenon in oversaturation conditions. At a certain time step, the inflows to a left turn cell and a through cell close to signal A are determined by their available spaces. All flows are restricted if either of them is unable to accommodate its allocation of flow. In this illustration, the through cell has 13 vehicles and is fully occupied, and all flows are restricted even though the left turn cell still has 11 vehicle spaces available. This matches what happens in reality. Vehicles block the entrance of the through lane although there are one or more available spaces in the left turn bay.

Fig. 10 Through flow blocking left turn bay

2) Left turn blocked at an intersection

Spillback at signalized intersections may block left turns, as shown in Fig. 11. For example, at a certain time step, the conditional cell is full. So, left turn vehicles in Cell (2, 3, 7L) on the major street that desire to go to the minor street are blocked even it is green time. This causes the problem of defacto red (i.e., the signal might as well be red because they cannot move [21]). Such a phenomenon is common in two-way oversaturated arterials and is simulated by CCTM successfully.

Fig. 11 Westbound left turn blocked by spillback in conditional cell

4 Validation of CCTM by highway capacity software 2000

To validate CCTM, it is compared with Highway Capacity Software 2000 (HCS) in terms of travel speed. Three scenarios of traffic demand are input into the HCS-arterials routine, and resulting travel speeds are compared with CCTM, as listed in Table 3. 

Table 3 Comparison between CCTM and HCS in terms of travel speed

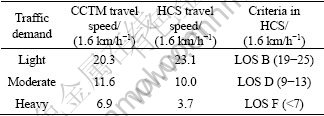
For light traffic demands in the HCS, the level of service (LOS) is B. In CCTM, vehicles in cells dissipated with cycle length, and there were no blockages. This is exactly what drivers expect at LOS B. For moderate demands in the HCS, the LOS is D. In CCTM, the number of vehicles in cells always reaches the capacity (13 vehicles), and there are occasional blockages. Blockages cause additional delay, which decreases travel speed. For heavy traffic demands in the HCS, the LOS is F. The network processes the traffic demand poorly and travel speeds are very slow. In CCTM, cells are always full for a long time. Spillback occurs frequently and causes delay to increase, which degrades the speed substantially. Hence, the simulation in CCTM is consistent with the criteria of the HCS at three traffic demand as expected. The consistency between the HCS 2000 and CCTM shows that CCTM is a reliable model for simulating two-way traffic flow in oversaturated conditions.

5 Conclusions

1) A new traffic flow model – the conditional cell transmission model (CCTM) for two-way arterials in oversaturated conditions, was developed. CCTM includes the addition of a conditional cell at an intersection to simulate spillback and blockages. The cell exists conditionally, depending on whether or not there is a spillback at an intersection. In other words, if spillback happens, the conditional cell exists and stores the vehicles which spillback into the intersection; if there is no spillback, the conditional cell will not exist. When the conditional cell exists, CCTM determines whether there is an acceptable gap inside the conditional cell to allow vehicles to cross it.

2) To test the performance of CCTM, a series of experiments were designed and performed for a multilane, two-way, three-signal sample network. The results indicate that CCTM can accommodate various traffic demands and reveal how CCTM delineates phenomena in oversaturated conditions. In light conditions, there is no difference between the CTM and CCTM. However, the delay of left turns is underestimated by 40 % in moderate conditions and by 58% in oversaturated condition when using the CTM rather than CCTM.

3) Many additional enhancements can be made to the model. A possible future work is to analyze the length and shape of cells. Another obvious example is to take account of random variations of built-in parameters in CCTM. It would be informative to use field data to calibrate CCTM. Finally, another option is to add operation parameters to CCTM. For example, peak hour factor and arriving type can be formulated into a function of traffic demands to reflect variations in traffic demand whereas the current model assumes it to be constant. With these new features, CCTM can be developed into useful simulation tool to support new research to further understand oversaturated traffic operations, their origins and potential means of mitigating their impacts.

References

[1] NIU Wen-yuan. Fifteen large cities lose nearly one billion RMB per day due to traffic congestion [ER/OL]. http://bkb.ynet.com/article.jsp?oid=72370228.

[2] PIGNATARO L J, MCSHANE W R, CROWLEY K W, LEE B, CASEY T W. Traffic control in oversaturated street networks [R]. Washington D C: Transportation Research Record, National Research Council, 1978.

[3] TANG Tie-qiao, LI Chuan-yao, HUANG Hai-jun, SHANG Hua-yan. Macro modeling and analysis of traffic flow with road width [J]. Journal of Central South University of Technology: 2011, 18(5): 1757-1764.

[4] LIU Tian-liang, HUANG Hai-jun, TIAN Li-jun. Microscopic simulation of multi-lane traffic under dynamic tolling and information feedback [J]. Journal of Central South University of Technology: 2009, 16(5): 865-870.

[5] YIN Y F, LIU H X, LAVAL J A, LU Xiao-Yun, LI Meng, PILACHOWSKI J, ZHANG Wei-Bin. Development of an integrated microscopic traffic simulation and signal timing optimization tool [D]. Berkeley: University of California, 2007.

[6] GURUPACKIAM S, JONES L S, FONSECA J D. Investigating initialization times, repetitions, and MOE variability in simulation of under saturated and saturated traffic signals [C]// 6th International Symposium on Highway Capacity and Quality of Service Social and Behavioral Sciences, Stockholm, 2011: 1-2.

[7] LIGHT M J, WHITHAM B. On kinematic waves. I: Flow movement in long rivers; II: A theory of traffic flow on long crowed roads [C]// Proceedings of Royal Society of London (Series A). London: The Royal Society, 1955: 281-345.

[8] RICHARDS P I. Shockwaves on the highway [J]. Operation Research, 1956, 4(1): 42-51.

[9] SHI Feng, ZHOU Wen-liang, LIU Fen-fang, DENG Lian-bo. Two-lane roundabout traffic flow characteristics based on cellular automaton [J]. Journal of Central South University: Science and Technology, 2010, 41(4): 1616-1622. (in Chinese)

[10] CHEN Qian, WANG Wei, Application of fuzzy optimization method based on CTM for traffic trunk line control under special events [J]. Journal of Southeast University, 2008, 138(5): 861-865. (in Chinese)

[11] LO H K. A novel traffic signal control formulation [J]. Transportation Research Part A, 1999, 33(6): 433-448.

[12] LO H K. A cell based traffic control formulation: strategies and benefits of dynamic timing plans [J]. Transportation Science, 2001, 35(2): 148-164.

[13] WENG Ping. Conditional cell transmission model for two way arterials in oversaturated conditions [D]. USA: University of Alabama, 2010.

[14] LO H K, CHOW A H F. Control strategies for oversaturated traffic [J]. Journal of Transportation Engineering, 2004, 130(4): 462-477.

[15] LI Z, CHANG G L. Modeling arterials signal optimization with enhanced cell transportation formulations [C]// Transportation Research Board 89th Annual Meeting. Washington D C: National Research Council, 2010: 1-2.

[16] LIN W H, AHANOTU D. Validating the basic cell transmission model on a single freeway Link [D]. Berkeley: University of California, 1995.

[17] SMILOWITZ K R, DAGANZO C F. prediction of time dependant traffic backups and other reproducible traits in experimental highway data [D]. Berkeley: University of California, 1999.

[18] ROESS R P, PRASSAS E S, MCSHANE W R. Traffic engineering. third edition [M]. New Jersey: Prentice Hall, 2004: 650.

[19] U.S. Department of Transportation. Manual on uniform traffic control devices [M]. Washington D C: Federal Highway Administration, 2009: 66800.

[20] U.S. Department of Transportation. Traffic analysis toolbox volume III: Guidelines for applying traffic microsimulation modeling software [M]. Washington D C: Federal Highway Administration, 2004: 85.

[21] ABU-LEBDEH G, BENEKPOHAL R. Development of a traffic control and queue management procedure for oversaturated arterial [C]// Transportation Research Board Annual Meeting. Washington D C: National Research Council, 1997: 119-126.

(Edited by YANG Bing)

Foundation item: Project(51108343) supported by the National Natural Science Foundation of China; Project(06121) supported by University of Transportation Center for Alabama, USA

Received date: 2011-10-25; Accepted date: 2012-01-13

Corresponding author: YANG Qun, Associate Professor, PhD; Tel: +86-13818716179; E-mail: qunyang.w@tongji.edu.cn