
Structure and second-order nonlinearity of GeS2-Ga2S3-X2S3 (X=P, As, Sb) chalcogenide glasses
GONG Yue-qiu(龚跃球), GUO Hai-tao(郭海涛), ZHAO Xiu-jian(赵修建)
Key Laboratory of Silicate Materials Science and Engineering, Ministry of Education,Wuhan University of Technology, Wuhan 430070, China
Received 10 April 2006; accepted 25 April 2006
Abstract: To find new chalcogenide glass possessing larger second-order non-linearity, glasses with compositions Ge-Ga-X-S (X=P, As, Sb) were prepared via melt quenching technique. The amorphous nature of all the compositions of the as-quenched glasses was confirmed by X-ray diffraction(XRD). The glassy thermal properties of the as-quenched glasses were established by differential thermal analyses(DTA). The glass structure was studied by RAMAN spectra and the second order nonlinearity was studied by the Maker Fringe method after the electron beam poling(EBP) and electric/temperature field poling(ETFP) respectively. Additions of various pnicogen atoms into the Ge-Ga-S glasses lead to the difference in the second order nonlinearity of the glass. It’s found that glasses with different structures result in different SHG intensities, and even more, a large second order nonlinear susceptibility c(2) of about 9 pm/V was obtained for all the glasses and the reasons for such a large susceptibility were analyzed.
Key words: chalcogenide glass; pnicogen; poling; SHG
1 Introduction
It’s well known that the second order nonlinearity such as second harmonic generation(SHG) should be forbidden in the amorphous materials such as glass because of its inversion symmetry. However, since the first discovery by OSTERBERG and MARGULIS[1] of efficient SHG in a variety of Si-Ge glass fibers on training with optical fields have generated considerable interest in the physics and applications of this unexpected phenomenon.
Different methods of poling have been successfully used to induce a permanent c(2) susceptibility in glasses [2]: thermal poling, UV poling, proton implantation, electron beam irradiation and corona discharge-assisted poling. Among these methods, thermal poling has been used extensively during the past years, while the electron-beam technique can easily achieve the quasi phase matching, which is a tightly controlled periodic modulation in the induced nonlinearity.
There are two popular explanations about the origin of the SHG in glass. One is that the external excitation field results in the emergence of a spatially modulated local direct-current electric field, Edc, which, via a third-order nonlinearity (χ(3)) induces a spatially modulated second-order nonlinearity(χ(2)∝3χ(3)Edc)[3]. The other is that collective orientation of hyper-polarizable entities (such as bond, dipole, defect, nano-crystallite) leads to the creation of a macroscopic χ(2) susceptibility[2].
Chalcogenide glasses have larger χ(3) than other inorganic glasses (about two orders of magnitude larger than that of silica)[4]. It’s certain that they should have larger SHG efficiencies. Actually, LIU et al[5] observed SHG in the Ge-As-S chalcogenide glasses by the methods of electron-beam irradiation and recently, GUIGNARD et al[6] also observed SHG in the Ge-Ga-Sb-S chalcogendie glasses by thermal poling. These observations open up the prospect of chalcogenide glasses as important promising materials for nonlinear optical frequency-conversion devices and the all-optical switching.
The glasses from Ge-Ga-S system, have a large solubilities of rare-earth ions[7] are promising because of their wider transparency in the visible region. Moreover, the pnicogen atom has three valence electrons, which made its compound have large polarizing abilities. From these points of view, we add the pnicogen into the Ge-Ga-S glass, and studied their structure and second order nonlinearity after effective electron beam irradiation poling (EBP) and electric/temperature field poling(ETFP), respectively. This paper is focused on the same/different chalcogenide glasses, after different/same poling method, and the difference of the SHG intensity and reasons.
2 Experimental
Glasses of various compositions (see Table 1) in the system Ge-Ga-X-S (X=P, As, Sb) were prepared via a melt quenching technique. The amorphous nature of all the as-quenched products of different compositions was confirmed by X-ray powder diffraction(XRD). The index of refraction of all the samples were measured at the spectro-ellipsometer(W-VASE). The characteristic temperatures were determined by the DSC-TG (Netzsch STA 449C). RAMNA spectra of the glasses were measured with RAMAN Spectrometer (Renishaw RM-1000) in back (180?) scattering configuration.
As for the Maker Fringe measurement[8], all the three glass plates (1 mm in thickness and 10 mm in width) were poled by electron beam irradiation (30 kV, 15 nA, 20 min) and electric/temperature field poling (200-300 ℃, 6 kV, 30 min), detail of the poling method can be seen elsewhere[5,6], then all the poled samples were measured in our own laboratory by the Maker Fringe device (Fig.1) just like LIU et al[6] did.
3 Results and discussion
All the samples are amorphous according to the results of the XRD. Table 1 shows the refractive indices and the thermal properties of all the samples. From the thermal properties, the GeGaAsS glass has good ability to form glass.
The RAMAN spectra of Ge-Ga-X-S glasses are presented in Fig.2. All the glasses are dominated by the presence of the band located at about 340 cm-1, which is related to the overlapping of the symmetric stretching modes of the tetrahedral [GeS4] and [GaS4][9]. A company peak at 370 cm-1 of GeS2 associated to the vibrations of the tetrahedral bound by their edges.
The band located at 430 cm-1 is related to the vibration of structural S3Ge-S-GeS3 units when the
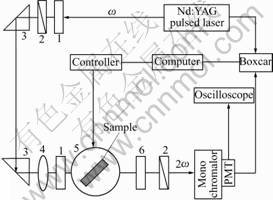
Fig.1 Sketch of Maker Fringe device: 1 532 nm filter; 2 Polarizing lens; 3 Split lens; 4 Focus lens; 5 Samples; 6 1064 nm filter
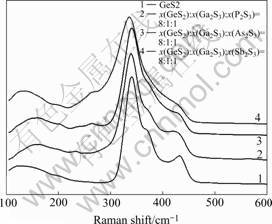
Fig.2 RAMAN spectra of Ge-Ga-X-S glasses
tetrahedral are connected by their corners. It’s clear that with the addition of pnicgen atoms, its intensity became lower and shifter to the low wavelength, which means that the structure of the glass is not so strong as the GeS2, whose structure is merely tetrahedral. While going down towards the lower wave numbers, the shoulder at 260 cm-1, especially for the Ge-Ga-Sb-S glass, is associated to the stretching vibration of the homopolar bond Ge-Ge in the S3Ge-GeS3 units[10]. A typical feature of the main band at about 340 cm-1 is that it became even wider with the addition of pnicgon atoms, which involves rising randomness of the amorphous structure. That the structure of Ge-Ga-X-S is not so rigid and more amorphous than the GeS2 glass leads to the large second
Table 1 Composition and characteristic of Ge-Ga-X-S glasses

order nonlinearity in the former glass system. Another feature of the main band is that it shifts to the lower band (from 340 cm-1 to 332 cm-1) with the addition of pnicgon atoms. It can associate either with the increase of the intermolecular interactions or to the distortion more accentuated of the structural entity[11].
The shapes of RAMAN spectra of the Ge-Ga-Sb-S glass in the lowest frequency domain (100-250 cm-1) is much different from others, which presents a deficit in sulfur or a typical RAMAN feature of mental antimony. That is, the spectra of S-deficient glasses have some peaks in the range of 150-250 cm-1 related to the formation of homopolar bonds[12]. For example: the RAMAN band at 163 cm-1 can be connected with vibrations of Sb-Sb bonds and band at 208 cm-1 could be related to the vibration of bonds linking two dissimilar elements like Sb-Ga (Sb-Ge). As for the band at about 140 cm-1, according to the result of Ref.[13], we can tentatively ascribe it to the RAMAN spectra of mental antimony. Just because the glass containing of antimony present so many homopolar bonds associated with different structural organization, the glass has a large nonlinearity. It will be analyzed in detail later.
Fig.3 shows the second order nonlinearlity χ (2) dependent of Ge-Ga-X-S glasses by different poling methods. The χ(2) values are calculate according to Ref. [14]. The relaxation time of the ETFP is calculated according to Ref.[5]. All the calculated results of the glasses are listed in Table 1. It’s clear that for the same poling condition, the identical sample has a relatively different χ(2) values. The reasons are from the following two aspects. First, the glass structure decides the stability of second order nonlinearity just like the result of relaxation time in Fig.2. From the RAMAN analyses hereinbefore, the Ge-Ga-Sb-S has a relatively loose structure, easy to be poled. But just because of the same reason, its relaxation time is also very short. Second, according to Ref.[15], two conditions must be satisfied in order to build up a frozen-in field. One is that there must exist movable cation in the glass, the other is that no other movable ions enter the depletion layer after it is formed. It is clear that during the ETFP, the first condition would no longer be satisfied in the glass including of phosphorus and arsenics than antimony, while for the EBP, the continuous injection of electron ions from near the anode surface destroys the formation of the depletion layer, especially for the glass containing antimony, and thus no high frozen-in electric field can be built up. Another possible reason for the glass including antimony has a small nonliearity in the EBP maybe due to its large electric conduction, which causes the inner frozen-in electric field difficult to be established. Therefore, different poling method will lead to different SHG intensity for the same sample because of its structure difference.
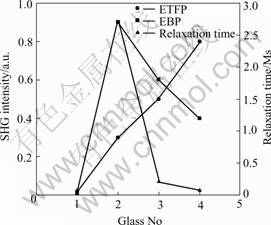
Fig.3 SHG intensity and relaxation time of Te-Ga-X-S glasses (X=P, As, Sb)
References
[1] OSTERBERG G, MARGULIS G. Dye laser pumped by Nd:YAG laser pulses frequency doubled in a glass optical fiber [J]. Opt Lett, 1986, 11(8): 516-518.
[2] QUIQUEMPOIS Y , NIAY P, DOUAY M. Advances in poling and permanently induced phenomena in silica-based glasses [J]. Current Opinion in Solid State and Materials Science, 2003, 7: 89-95.
[3] MYERS R S, MUKHERJEE N, BRUECK S R J. Large second-order nonlinearity in poled fused silica [J]. Opt Lett, 1991,16(22): 1732-1734.
[4] SMEKTALA F, QUEMARD C, LENEINDRE L. Chalcogenide glasses with large non-linear refractive indices [J]. Journal of Non-Crystalline Solids, 1998, 239: 139-142.
[5] LIU Q M, GAN F X, ZHAO X J. Second-harmonic generation in Ge20As25S55 glass irradiated by an electron beam [J]. Opt Lett, 2001, 26(17): 1347-1349.
[6] GUIGNARD M, NAZABAL V, QUIQUEMPOIS Y. Second-harmonic generation of thermally poled chalcogenide glass [J]. Opt Express, 2005, 13(3): 789-794.
[7] HEO J, JOONG M, Y. Raman spectroscopic analysis on the solubility mechanism of La3+ in GeS2–Ga2S3 glasses [J]. J Non-Cryst Solids, 1998, 238: 115-123.
[8] MAKER P D, TERHUNE R W, SAVAGE C M. Effects of dispersion and focusing on the production of optical harmonics [J]. Phys Rev Lett, 1962, 8: 21-22.
[9] LUCOVSKY G, GALEENER F L, KEEZER R C. Structural interpretation of the infrared and Raman glasses in the alloy system Ge(1-x)Sx [J]. Phys Rev B, 1974, 10: 5134.
[10] TAI H Z, ZHAO X J, JING C B. Raman spectroscopic study on the microstructure of GeS2-Ga2S3-KCl glasses [J]. Journal of Molecular Structure. 2004, 697: 23-27.
[11] JULIEN C, BARNIER S, MASSOT M. Raman and infrared spectroscopic studies of Ge-Ga-Ag sulphide glasses [J]. Mat Science and Eng B, 1994, 22(5): 191.
[12] KOTSALAS I P, PAPADIMITRIOU D, RAPTIS C. Raman study of photostructural changes in amorphous GexSb(0.4-x)S0.6 [J]. Journal of Non-Crystalline Solids, 1998, 226(1-2): 85-91.
[13] LANNIN J S. Raman scattering properties of amorphous As and Sb [J]. Phys Rev B, 1977, 15(8): 3863.
[14] NASU H, MATSUOKA J, KAMIYA K. Second- and third-order optical non-linearity of homogeneous glasses [J]. Journal of Non-Crystalline Solids, 1994, 178: 23-30.
[15] XU Z L , LIU L Y, HOU Z J. Influence of different poling methods on the second-order nonlinearity in fused silica glasses [J]. Optics Communications, 2000, 174: 475-479.
(Edited by PENG Chao-qun)
Foundation item: Project(50125205) supported by the National Natural Science Foundation of China
Corresponding author: ZHAO Xiu-jian; Tel: +86-27-87652553; Fax: +86-27-87669729; E-mail: opluse@mail.whut.edu.cn